Сравнение способов инициализации начальных точек на генетическом алгоритме оптимизации

Введение. Генетический алгоритм глобальной оптимизации [1] отличается от остальных тем, что хорошо работает в экономике, финансах, банковской сфере. В генетическом алгоритме точки представлены в виде булевых строк. Эти строки можно формировать по-разному. Можно формировать напрямую, с помощью случайных последовательностей (с равномерным законом распределения). Можно разбросать точки с помощью случайных последовательностей (с равномерным законом распределения) в пространстве вещественных чисел, а потом преобразовать вещественные числа в булевые. Исследования проводились на функции Акли, функции Растригина, функции Шекеля, функции Гриванка и функции Розенброка [2]. ЛПτ последовательность [3], UDC последовательность, равномерный случайный разброс – очень интересные и эффективные алгоритмы разброса начальных точек. Последние исследования в этой области проводились в работах [4]. Эти исследования применялись к конкретным практическим задачам, не ставилась цель в усреднении данных параметров, в тестировании на большом количестве практических задач сложного вида тестируемой фукнции [5]. ЛПτ-последовательности – это алгоритм разброса точек на основе матрицы неприводимых многочленов Маршала. UDC последовательности – это алгоритм абсолютно равномерного распределения точек по всем координатам в многомерном пространстве [6] независимо от количества разбрасываемых точек [7]. Равномерный случайный разброс [8] – это стохастический алгоритм разброса точек, использующий нормальный закон распределения.

Описание параметров . В работе использовались лучшие параметры генетического алгоритма глобальной оптимизации [9]:

• 1.    Селекция – турнирная 4 участника.

• 2.    Рекомбинация – 2-точечная, вероятность скрещивания – 0,8.

• 3.    Вероятность мутации 0,001.

• 4.    Бинарное кодирование.

В работе использовались дополнительные параметры:

• 1.    Размер пространства исследуемой закономерности – 2.

• 2.    Общее количество разбрасываемых точек (булевых строк) – 50.

• 3.    Максимальное число шагов алгоритма (поколений) – 200.

• 4.    Точность нахождения экстремума – 0,0001.

• 5.    Количество повторных запусков алгоритма – 400.

• 6.    Границы исследуемой области от –45 до +45 по каждой координате.

В работе использовались 6 способов инициализации:

• 1- й способ: с помощью случайных последовательностей (с равномерным законом распределения) получают вещественное число от 1 до 100. Если полученное число будет меньше 50, то соответствующий бит булевой строки [10] принимает значение 1, иначе 0. Так получаются булевые строки (рис. 1).

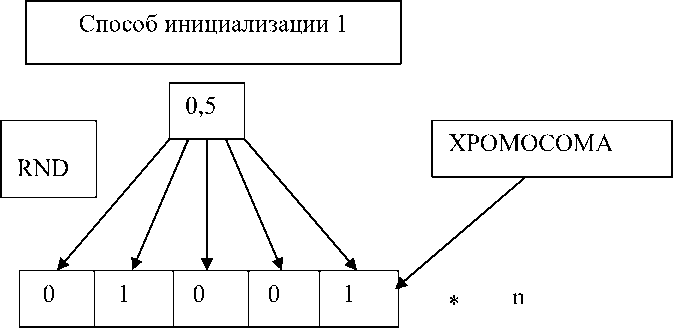
Рис. 1. Первый способ инициализации

Fig. 1. The first way to initialize

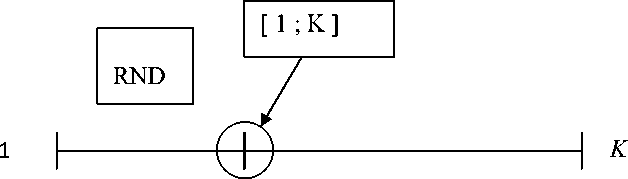
2-й способ: с помощью случайных последовательностей [11] получают вещественное число от 1 до K, где K – максимальное вещественное число, получившееся, если бы каждый бит булевой строки был равен 1. Затем это вещественное число преобразуют в булевую строку по правилам преобразования. Так получаются булевые строки (рис. 2).

Способ инициализации 2

0

1

0

0

1

Рис. 2. Второй способ инициализации

Fig. 2. The second way to initialize

*n

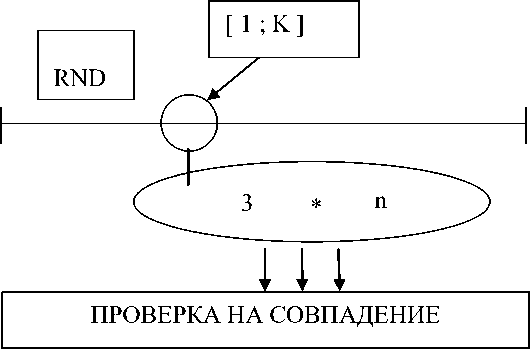
3-й способ – это тот же 1-й способ, но с проверкой булевых строк на повторяемость (рис. 3).

Способ инициализации 3

• 3,    5, … , n

ПРОВЕРКА НА СОВПАДЕНИЕ

Рис. 3. Третий способ инициализации

Fig. 3. The third way to initialize

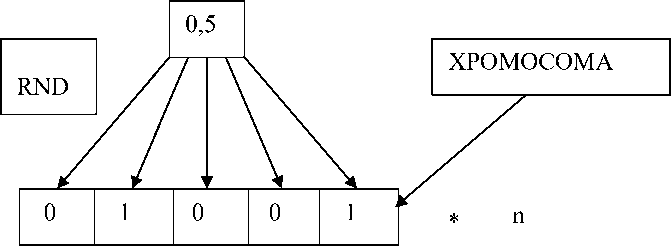
4-й способ – это тот же 2-й способ, но с проверкой вещественных чисел на повторяемость (рис. 4).

Способ инициализации 4

0

1

0

0

1

Рис. 4. Четвёртый способ инициализации Fig. 4. Fourth Initialization Method

5-й способ: с помощью ЛП τ -последовательности получают вещественное число от 1 до 100. Если полученное число меньше 50, то соответствующий бит булевой строки будет 1, в противном случае 0. Так получаются булевые строки (рис. 5).

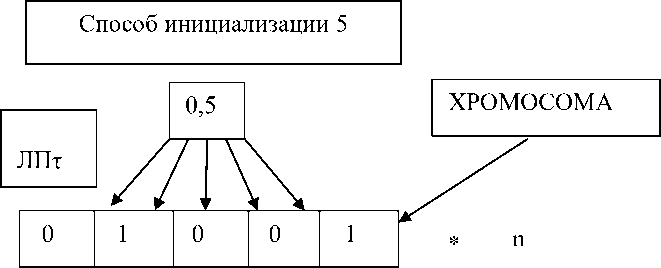
Рис. 5. Пятый способ инициализации

Fig. 5. Fifth Initialization Method

6-й способ: с помощью ЛП τ -последовательности получают вещественное число от 1 до K, где K – максимальное вещественное число, получившееся, если бы каждый бит булевой строки был равен 1. Затем это вещественное число преобразуют в булевую строку (рис. 6).

Способ инициализации 6

[ 1 ; K ]

ЛП τ

j K

3      *

n

0

1

0

0

1

Рис. 6. Шестой способ инициализации

Fig. 6. Sixth way to initialize

*n

На выходе мы получаем массивы математических ожиданий и среднеквадратических отклонений качества решения для разных функций и оптимизационных алгоритмов [12]. Под качеством решения понимается среднестатистическая ошибка нахождения экстремума [13].

Последние эксперименты в данной области проводились в работах [7]. В данных трудах бинарные строки формировались без учета проверки на повторяемость.

Экспериментальная часть . Способы инициализации сравниваются между собой на генетическом алгоритме, по математическому ожиданию, на первой функции. Определяется лучший способ инициализации по шестибальной шкале. Затем они сравниваются между собой на второй функции и т. д.

После этого суммируются заработанные баллы по всем функциям для каждого способа инициализации [14]. Чем больше получится сумма, тем лучшее место займёт тот или иной способ инициализации. Заработанные таким образом места фиксируются в табл. 1 и 2.

Таблица 1

Процент нахождения экстремума для алгоритма по абсолютному значению

		Способы инициализации (I)						Лучшая I
		1	2	3	4	5	6
e я я к к	1	4,00	3,50	2,75	2,25	3,50	3,25	1
	2	7,25	7,50	7,25	7,75	8,50	7,25	5
	3	0	0	0	0	0	0	–
	4	0	0,25	0	0,75	1,00	0,25	5
Итого								5

Таблица 2

Качество решения для Генетического алгоритма по абсолютному значению

Функция		Способы инициализации (I)						Лучший I по М	Лучший I по σ
		1	2	3	4	5	6
1	М	0,2431	0,2453	0,2511	0,2401	0,2231	0,2370	5	2
	σ	0,2127	0,2035	0,2221	0,2177	0,2076	0,2077

2	М	0,0613	0,0585	0,0629	0,0586	0,0533	0,0598	5	5
	σ	0,0512	0,0495	0,0725	0,0553	0,0310	0,0456
3	М	0,5001	0,5478	0,5091	0,4904	0,4433	0,4455	5	5
	σ	0,3947	0,5188	0,3718	0,3459	0,0055	0,0422
4	М	1,7635	1,7237	1,7866	1,7827	0,9066	1,9681	5	5
	σ	1,5675	1,7093	1,6367	1,6068	0,4152	1,8819
Места по М		5	4	6	2	1	3
Места по σ		3	3	5	4	1	2
Итого мест		5	4	6	3	1	2

Потом весь цикл повторяется для среднеквадратического отклонения ( σ ). После этого заработанные места по математическому ожиданию (M) и по σ суммируются и снова сравниваются между собой [15]. В итоге мы будем знать:

• 1.    Какой способ инициализации лучший для каждой из функций при использовании генетического алгоритма, как по математическому ожиданию, так и по σ .

• 2.    Какие способы инициализации лучшие, какие худшие в среднем для всех четырёх оптимизационных функций, как по математическому ожиданию и σ , так и в общем при использовании генетического алгоритма.

Результаты . Как мы знаем, цель любого оптимизационного алгоритма заключается в том, чтобы найти экстремум как можно быстрее, точнее, дешевле и надёжнее.

Процент нахождения экстремума, в среднем, по всем оптимизационным функциям лучше у способа инициализации 5 (табл. 2). Отсюда следует, что у способа инициализации 5 самая большая надёжность (вероятность) отыскания экстремума.

С точки зрения быстроты можно сказать, что при 50-ти точках алгоритм просчитывает 200 шагов (поколений), в среднем, за 1/400 с.

Точность – это обратная характеристика ошибки. Точность тем выше, чем меньше ошибка. Чем выше получается точность, тем меньше число принимает характеристика по шестибальной шкале, а это означает, что характеристика лучше.

Для генетического алгоритма (табл. 1) самая маленькая ошибка нахождения экстремума (качество решения) по математическому ожиданию для 1-й функций у способа инициализации 5. Это означает, что у способа инициализации 5 самая высокая точность нахождения экстремума. Для генетического алгоритма самая большая точность нахождения экстремума по математическому ожиданию для функций 2, 3, 4 тоже у способа инициализации 5. В среднем, для генетического алгоритма самая высокая точность нахождения экстремума у способа инициализации 5.

Для генетического алгоритма самая маленькая ошибка нахождения экстремума по σ для функции 1 (погрешность) у способа инициализации 2, а для функции 2, 3, 4 – у способа инициализации 5. В среднем, для генетического алгоритма самая маленькая погрешность того, что полученное значение математического ожидания есть среднестатистическое значение математического ожидания у способа инициализации 5.

Так как, в среднем, для генетического алгоритма самая высокая точность нахождения экстремума и самая маленькая погрешность полученного результата у способа инициализации 5, то, в среднем, способ инициализации 5 является лучшим способом инициализации для генетического алгоритма и занимает первое место.

Чтобы попытаться сравнить способ инициализации 5, например, с используемым сейчас способом инициализации 1 в числовом виде, были сделаны сравнения этих способов инициализации в процентах относительно способа инициализации 1 по каждой функции, а потом взято среднее арифметическое этих процентов по всем функциям.

В результате оказалось, что в генетическом алгоритме способ инициализации 5 лучше способа инициализации 1 в среднем на 20 %.

По результатам можно сделать вывод, что применение проверки в булевой инициализации не приводит к положительному результату, а в вещественной – приводит.

Заключение. Проанализирован генетический алгоритм глобальной оптимизации. Исследования проводились на функции Акли, функции Растригина, функции Шекеля, функции Гриванка на шести способах инициализации булевых строк с использованием трех алгоритмов разброса начальных точек: ЛП τ последовательность, UDC последовательность, равномерный случайный разброс. Проведённые исследования показали, что в среднем способ инициализации 5 является лучшим способом инициализации для генетического алгоритма, из чего следует, что способ инициализации 5 является очень перспективным. Необходимо учесть, что способ инициализации 5 построен на неслучайном алгоритме разброса точек – ЛП τ -последовательности. Это даёт стимул для дальнейшего исследования ЛП τ -последовательности и лишний раз подтверждает эффективность её применения.