Сравнение статистических оценок свойств различных морфологических фильтров, построенных на основе мозаичных моделей изображений

В рамках морфологии Пытьева [1] традиционно считается, что морфологическая форма имеет несколько альтернативных представлений и одинаково (эквивалентно) определяется тремя своими описаниями: мозаичным разбиением кадра, оператором проекции и линейным подпространством.

В более широком морфологическом подходе [2], который мы предлагаем здесь рассмотреть, морфологический оператор и морфологическая модель (и даже разные представления одной морфологической модели) перестают однозначно определять друг друга.

Соответственно, оценка сложности модели более не связана напрямую с характеристиками фильтра, но при этом между ними, очевидно, должна быть установлена некая связь. Для этого в соответствии с методологией работы [3] нам необходимы две характеристики – оценка сложности модели (мера сложности) и оценка силы действия фильтра (степень модификации).

В данной работе мы введем такие оценки и проведем сравнение статистических оценок свойств раз- личных морфологических фильтров, построенных на основе мозаичных моделей. При этом мы сначала убедимся, что оценки сложности форм и степени модификации для пытьевских операторов действительно связаны. Далее мы проведем сравнение линейных и нелинейных мозаичных фильтров по силе фильтрации, а также исследуем вопрос о связи степени упрощения и сложности модели для диффузных операторов.

Степень модификации фильтра и ее связь со сложностью модели

Ранее в работе [3] мы рассмотрели эту проблему следующим образом.

Пусть имеется метрическое пространство образов 〈 Ω , d Ω 〉 с метрикой d Ω . Пусть также задано множество простейших образов O ⊆ Ω , определен проектор на множество O

ψ O : Ω→ O , ψ O ² =ψ O .

Тогда для любого образа a ∈ Ω его проекцию ψ O a будем называть предельным упрощением, а сам проектор ψ O – оператором предельного упрощения.

Неусложняющим оператором на Ω назовем такой оператор ψ : Ω → Ω , который:

– сохраняет простейшие образы

∀ o ∈ O , ψ o = o ;

– переставим с оператором предельного упрощения

ψψO= ψOψ = ψO;

– монотонно не увеличивает расстояние до предельного упрощения

∀ a ∈ Ω , d Ω ( ψ a , ψ O a ) ≤ d Ω ( a , ψ O a ) .

Иными словами, неусложняющий оператор – это сжимающее отображение на Ω , центрированное относительно множества простейших образов. Для краткости будем называть неусложняющие операторы упрощающими фильтрами (simplification filter, simplifier).

Поскольку множество неусложняющих операторов Ψ также специфично для каждой конкретной морфологии, можно сказать, что любая морфологическая система должна описываться уникальным набором элементов 〈 Ω , d Ω , O , ψ O , Ψ 〉 , находящихся между собой в следующих отношениях:

O ⊆ Ω ,

Ψ={ψ:Ω→Ω},

ψO ∈Ψ,ψ0 :Ω → O,ψ2o = ψO,

∀ o ∈ O , ψ o = o ,

∀a∈Ω,dΩ (ψa,ψOa) ≤ dΩ (a,ψOa).

Введем две характеристики, описывающие воздействие фильтра ψ ∈ Ψ на некоторый конкретный образ z ∈ Ω :

– степень модификации образа z фильтром ψ

J ( ψ , z ) = d Ω ( ψ z , z );

– cложность образа ψ z (чем меньше эта сложность, тем сильнее упрощение z фильтром ψ )

Q ( ψ , z ) = Q ( ψ z ) = d Ω ( ψ z , ψ O z ) .

Эти две характеристики определяют два, вообще говоря, различных отношения частичного порядка на множестве фильтров:

– отношение частичного порядка ( ≤ M ) между фильтрами по степени модификации («модифицирует не слабее»):

ψ A ≤ M ψ B ^⇔ (by definition ) ∀ z ^∈ Ω : J ( ψ A z ) ≥ J ( ψ B z ) ;

– отношение частичного порядка ( ≤ S ) между фильтрами по степени упрощения («упрощает не слабее»):

ψ A ^≤ S ψ B ^⇔ (by defintiton ) ^∀ z ^∈ Ω : Q ( ψ A , z ) ^≤ Q ( ψ B , z ) .

Упрощающими модификаторами (УМ-фильтрами) будем называть такие фильтры, которые удовлетворяют следующим двум условиям:

– неусложнение

∀ z ∈ Ω , ∀ ψ ∈ Ψ : Q ( ψ z ) ≤ Q ( z );

– монотонная зависимость степени модификации от степени упрощения

∀ψA,ΨB ∈Ψ,∀z∈Ω,Q(ψA,z) ≤ ≤Q(ψB,z)⇔J(ψA,z)≥J(ψB,z).

Для таких УМ-фильтров два введенных отношения частичного порядка (по силе упрощения и по силе модификации) эквивалентны:

ψ A ≤ M ψ B ⇔ ψ A ≤ S ψ B .

В работе [3] мы показали, что большинство известных морфологических систем укладываются в такую схему описания, при которой морфологические фильтры являются УМ-фильтрами. Более того, мы показали, что некоторые свойства упрощающих фильтров, которые мы выше должны были постулировать, на самом деле автоматически следуют из условия монотонности модификации по упрощению. Это позволяет cчитать набор 〈 Ω , Ψ , J , Q 〉 более общим определением морфологической системы.

Морфологической системой на базе УМ-фильтров (УМ-морфологией) называется набор элементов 〈 Ω , Ψ , J , Q 〉 , находящихся между собой в следующих отношениях:

Ψ={ψ:Ω→Ω},ψI∈Ψ:∀z∈Ω:ψIz =z;

J : Ψ×Ω→ R , ∀ ψ ∈ Ψ , ∀ z ∈ Ω , J ( ψ I , z ) ≤ J ( ψ , z ), ψ≠ψ I ⇒ J ( ψ I , z ) < J ( ψ , z ).

Q : Ψ×Ω→ R , Q ( ψ , z ) = Q ( ψ z ) ⇐ Q : Ω→ R ;

Q ( ψ I , z ) = Q ( ψ I z ) = Q ( z );

∀ z ∈ Ω , ∀ ψ ∈ Ψ : Q ( ψ z ) ≤ Q ( z );

∀ψA,ψB∈Ψ,∀z∈Ω,Q(ψA,z)≤ ≤Q(ψB,z)⇔J(ψA,z)≥J(ψB,z).

Все необходимые свойства морфологических фильтров далее могут быть выведены из данного определения. При конкретной реализации J и Q описанным выше образом из данного определения автоматически получается приведенное ранее определение морфологической системы на базе 〈 Ω , d Ω , O , ψ O , Ψ 〉 .

УМ-морфологии – наиболее общий из до сих пор введенных нами формализмов для описания морфологических систем. Однако в данной работе он является для нас недостаточным, поскольку:

• а)    не проводит различия между моделями и операторами (все рассуждения ведутся только в терминах операторов);

• б)    введенные для операторов отношения порядка ( ≤ S ) и ( ≤ M ) являются отношениями частичного, а не полного порядка;

• в)    базовые для этих отношений абсолютные численные характеристики J ( v , z ) и Q ( v , z ) описывают не оператор V е V как таковой, а лишь его воздействие на некоторый конкретный образ z е Q ;

• г)    некоторые из мозаичных операторов вообще не являются упрощающими фильтрами в том смысле, который был описан выше (см. ниже случай нелинейной мозаичной фильтрации).

Для того, чтобы охарактеризовать на основе введенных критериев Q ( v , z ) и J ( v , z ) сам оператор V , необходимо либо взять некую статистику (экстремум, среднее, что-то еще) по всему ансамблю изображений Q , либо выбрать из каких-то соображений некий стандартный тестовый образ z * («пробный камень»), либо как-то сочетать эти два подхода.

Рассмотрим подход на основе статистического усреднения. Назовем оценки

J ⁰ М = L J ( V , z )^{р е} ( z ) dz ,

Q0(V) = n Q(V,z )P0(z) dz’ среднестатистическими по классу 0 с заданным распределением плотности вероятности po(z). На их основе по аналогии с морфологическими коэффициентами корреляции можно ввести:

• -    морфологический коэффициент степени модификации

к ( j , ® > ( v ) = J 0 ( v ) / J 0 ( v о ) ;

• -    морфологический коэффициент степени упрощения

к ( q ,0)(v) = Q@ (v)/ Q@(v i ), где VI - «слабейший» фильтр из V (не изменяет изображения), Vо — «сильнейший» фильтр из V (см. роль VO и VI выше и в [3]).

Меры сложности мозаичных форм

В рамках простейшей морфологии Пытьева [1] изображения рассматриваются как кусочнопостоянные функции вида

n f ( x, У ) = Е fFiX Fi( x, У ),                           (1)

i =1

где n - число областей разбиения F кадра Q на связные непересекающиеся области постоянной яркости, F ={ F i , „., F _n }; f = ( f F i , .., f _Fn ) ^T - вектор значений яркости, соответствующих каждой области разбиения; X Fi ( x, У ) е {0,1} - характеристическая функция i- й области яркости:

[ 1, если ( х, у ) е F ;

• X    f, ( х , У ) =f                                     (²)

• [ 0, впротивном случае.

Такие изображения называются мозаичными .

Морфологическое сравнение изображений по сложности традиционно [1] осуществляется в терми- нах отношения «не сложнее по форме», которое является отношением частичного порядка (некоторые изображения несравнимы по форме). Множество всех мозаичных форм образует по данному отношению алгебраическую структуру типа «решетка», в которой для любых двух форм F и G можно указать форму более сложную F л G и менее сложную Fv G. В терминах разбиений более сложные формы получаются из менее сложных разбиением областей, а менее сложные из более сложных - слиянием областей. В терминах множеств (классов) изображений F «не сложнее по форме» G, если F с G. В терминах проекторов F «не сложнее по форме» G, если PG PF=PF.

В работе [4] нами была введена методика расширения данного отношения до отношения полного порядка, основанная на обобщенном определении меры сложности структурного образа как неотрицательной величины, которая равна 0 для неструктурированного (неделимого) образа, монотонно увеличивается при таких последовательных преобразованиях образа, при которых число его элементов увеличивается, и монотонно уменьшается при таких последовательных преобразованиях образа, при которых число его элементов уменьшается. Подобными мерами сложности для мозаичного разбиения F кадра с площадями областей S _Fi = Sp i , i = 1, ..., n являются, например, количество информации Шеннона

• 1    (F) = -]^Pilog Pi,

или ОГО-сложность [4]

0 н(F) = Zi=1,„, n P-'(1 - Pi), связанная с метрикой оценки геометрических отличий (ОГО-метрикой) [5] следующего вида:

dH (F, G) = £ £ SijdH (Fi, G ),(5)

• j =1,..., l i =1,..., n

где d H ( F i , G j ) = S _Fi + S _Gj - 2 Sy - расстояние Хэмминга между областями разбиения F i и G y . Как мы показали в [5], ОГО-метрика может интерпретироваться как метрика редактирования мозаичных форм. Другой способ ее определения связан с реляционным способом описания мозаичных форм [6].

Определим предикат бинарного отношения «пикселы не принадлежат одной области»

• [ 0, если V i : X f- ( х , У ) = X f- ( u , v );

П _F ( x , У , u , v ) = s                                           (6)

• [ 1, впротивномслучае.

Пусть теперь имеется мозаичное изображение g формы G :

g ^{( х} , У ) = S g j X Gj^{( х} , У ). j =1,^, m

Соответствующая реляционная форма будет также иметь вид (6):

1 0, если V j : х Gj ( x , У ) = X Gj (u , v ); п g ( x , y , u , v ) = <

[ 1, впротивномслучае.

Рассмотрим базовую (по топологии) форму для пары этих форм W=Fл G, состоящую из набора областей парных пересечений Wij = Fi n Gj. Для нее можно записать п f (Wj, Wkl ) =

п g ( W j , W ki ) =

0, если i = k , т.е. W ij , W_kl e F i ;

1, в противном случае,

0, если j = l , т.е. W ij , W_kl e G j ;

• 1,    в противном случае.

  
  

Таким образом, симметричные четырехмерные функции превращаются в симметричные матрицы размера ( m x n)². В отличие от функциональной реляционной модели формы (6) мы будем называть модель (7) взаимной матричной реляционной моделью пары форм.

L ¹ -норма реляционной модели (6)

II п Fl I = HI Jn F (x, У, u, v) dxdydu dv также может быть выражена через параметры матричной модели (7)

mnmn

II п f || = ZZZZ S ij S ki п F (W ij , W kl ), j =1 i =1 l =1 k =1

где S ij , S kl – площади областей разбиения W ij , W kl .

Рассмотрим расстояние Хэмминга ( L ¹ -метрику) между реляционными формами п _F ( x, y, u, v ) и п G ( x, y, u, v ):

d „ ( п F , п G ) = ||п F ( x , У , u , v ) — п G ( x , У , u , v )|| =

= J J J 1| п _F ( x , y , u , v ) -п _G ( x , y , u , v )| dxdydudv

Для мозаичных форм выражение (8) можно пре- образовать к виду dп (пF , пG) = mnmn

= ZZZZ S ij S ki п F ( W j ,W k! ) — п G ( W j , W kl ) () j =1 i =1 l =1 k =1

В [6] мы показали, что nm d,(пF,пG) = ZZS-j (S+ Sj-2Sj) = i=1 j=1

nm

= ZZ S j d H ( F i , G j ) = d Н ( F , G ), i =1 j =1

т.е. расстояние Хэмминга ( L ¹ -метрика) между реляционными формами п f ( x, y, u, v ) и п g ( x, y, u, v ) по отношению «пикселы равны / не равны по яркости» в точности эквивалентно метрике оценки геометрических отличий (ОГО-метрике) между соответствующими мозаичными формами F и G вида (5).

Указанная связь (10) позволяет ввести для реляционных описаний формы абсолютную меру сложности. Учтем, что:

– для наиболее простой мозаичной формы O (единая область постоянного значения занимает весь кадр Q площади S ) || п O || = 0, т.к. ни одна пара пикселов не отличается по яркости, и модель п O содержит только нулевые связи;

– для наиболее сложной мозаичной формы I (предельное разбиение кадра, в котором каждый пиксел это отдельная область) || п I ||= S ² , т.к. все пары пикселов отличаются по яркости, модель п O содержит только единичные связи, и таких связей S x S = S ² .

Тогда нормированное значение L ¹ -нормы реляционной формы п _F

ЦH (пF ) = (||пF 11 - ||по 11) / (||пI 11 - ||пO 11) =

= d п ( п F , п O ) / d п ( п l , п O ) = ^ S i ( 1 - S i ) / S ² = (11) i =1,^, n

= z Pi(1 -Pi) = dH(F,O)/dH(I,O) = цH(F) i =1,^, n есть не что иное, как связанная с ОГО-метрикой нормированная ОГО-сложность цH (F) (4) мозаичной формы F, о которой шла речь выше.

Связь меры сложности, меры простоты и степени модификации в морфологии Пытьева

Используем морфологический коэффициент корреляции для получения статистических оценок интересующих нас показателей.

Ранее мы уже рассматривали задачу статистического усреднения квадрата нормы проекции при сравнении (пытьевском проецировании) изображений двух фиксированных форм [7].

Мы предположили, что для мозаичных изображений из F и G вида

f ⁽ x , y ) = Z f i х Fi⁽ x , y ); g ⁽ x , y ) = Z g j X G^{( x} , y ), i =1,^, n                                  j =1,^, m

H f II2 = Z f2Si,IIfG|Г = Z f2S^ i=1,^, n                      j=1,^, m fGj=\ z fSj I/Sj.j = 1,-,m

^ i =1,-, n       у справедливы следующие предположения о плотностях распределении значений яркости f1,…, fn:

• 1)    p ( f 1 , …, f n )= p ( f 1 )… p ( f n ) – величины f 1 ,…, f n независимы в совокупности;

• 2)    p ( f 1 ) =…= p ( f n ) – величины f 1 ,…, f n распределены одинаково;

• 3)    V i = 1 ,.., n: p (f i )= p (- f i ) - величины f ,,..., f n распределены симметрично относительно 0.

Далее мы определили среднеквадратичный эффективный коэффициент морфологической корреляции (СКМК) форм F и G как корень из отношения среднего квадрата нормы проекции изображения из F на форму G к среднему квадрату нормы проецируемого изображения:

KM(F,G ) Ц | Zg| I’)/( И I’).

Подставляя соответствующие выражения, получили:

K M ( F , G ) = £ £ = Z Z j .    (I’)

j =1,. mi =1,. n S j S     j =1,., mi =1,., n p j

Однако это еще всего лишь усреднение внутри формы проецируемого изображения. Если мы захотим на основе выражения для K M ² ( G, F ) (12) получить оценку K m ( q , ® ) ( P ( gF mean) ) для множества

0 = {g : g e G, G c M}, где M – класс всех мозаичных форм, нам придется взять математическое ожидание по всем возможным формам G c M со всеми возможными количествами и распределениями площадей областей мозаичного разбиения:

) =

^K M ( Q ,9)

( g , F , mean )

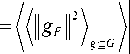
G c M

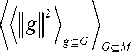
Такое выражение в явном виде вряд ли возможно аналитически вычислить. Поэтому мы предлагаем здесь обратиться к методу «пробного камня». Чтобы не усреднять по всем возможным формам, нужно выбрать одну опорную форму, сравнение с которой имело бы смысл для всех операторов.

По сути, именно это мы и сделали выше, когда вводили ОГО-сложность в форме (11):

Ц H (F) = Z Pi (1 - P') = i=1,. n                                                  (14)

= d n ( n F , П O ) / d n ( n I , П O ) = d H ( F , O ) / d H ( I , O ).

Как видно, здесь в качестве опорных форм используются самая простая и самая сложная формы O (одна область на кадр, все пикселы связаны) и I (каждый пиксел – отдельная область, и яркости пикселов никак не связаны).

Рассмотрим соответствующие значения K M ² , которые характеризуют форму F при ее сравнении с предельными формами O и I. Поскольку морфологический коэффициент корреляции асимметричен, мы имеем, помимо 3 тривиальных вариантов

K M ( F d I ) = 1, ■ K M ( O , I ) = 1, - K M ( O , F ) = 1,

3 нетривиальных варианта:

KM(F, O) =£ S =£ PF- i=1,.,n S       i=1,.,n

KM(I, о) =£ 712 = 1,(16)

i=1,..., SSS

KM(I,F) = (1/S) £ £(Si /SF) = i =1,.,n j=1,.,s

= (1/ S ) Z S F ( 1/ S F ) = n / S .

i =1,., n

Прежде всего, можно заметить, что (15) непосредственно связан с (4):

Ц H (F) = Z PFi (1 — PF ) = i =1,., n

= Z P F - Z P ’ = 1 - K M ( F , O ).

i =1,., n          i =1,., n

Таким образом, мы убедились, что в морфологии Пытьева мера сложности ц H ( F) непосредственно связана с мерой простоты K M ² ( F, O ). В самом деле, K M ² ( F, O )= K M ² ( F, P O ) сравнивает любую форму F с простейшей формой O , причем на самом деле здесь F – фильтруемая форма, а O выступает не в качестве формы, а в качестве стандартного тест-проектора P O . Поэтому K M ² ( F, O ) характеризует именно форму F , а не проектор P F , т.е. является характеристикой сложности (простоты) формы.

Нельзя не отметить, что связь

Ц H ⁽ F ) =||Я _F ^-п о||_л 1/||^п , ^-п о||_л 1 =

= d H ( F , о )/ d H ( I , о ) = 1 - K m ’ ( F , о )

является замечательным подтверждением внутреннего единства морфологического анализа Пытьева во всех его формах – атрибутной, реляционной, метрической и операторной. Это выражение также демонстрирует абсолютную внутреннюю связь между морфологическими инструментами сравнения по сходству / различию и сравнения по сложности. В некотором смысле для морфологического анализа данных это такое же «объединительное» равенство, как знаменитое тождество Эйлера e^{j п} +1=0 для комплексного анализа, поскольку оно сводит воедино, казалось бы, совершенно разные аспекты рассматриваемого предмета. В частности, (19) показывает, что ОГО-метрика действительно является не искусственной конструкцией, а естественной метрикой на множестве форм, поскольку она напрямую связана не только с мозаичным и реляционным представлением форм, но и с морфологическим проектором, который неустраним в любых вариантах морфологического анализа и является самой его базовой сердцевиной.

Рассмотрим теперь K M ² ( I, F ) = K M ² ( I, P F ), который, в отличие от K M ² ( F, O ), характеризует как раз не форму F , а проектор P F , причем является характеристикой проектора с точки зрения силы (степени) упрощения. Легко заметить, что (13) приводится к (17) путем выбора 0 ={ I }, т.е. сужения задачи усреднения по всему ансамблю форм до задачи усреднения действия оператора по выбранной тестовой форме:

KM(Q,I) (PF ) = (||gF|Г) /(I|g| f) , (’0) \ I g c I \ / g c I откуда, с учетом известной оценки дисперсии выборочного среднего нормально распределенной величины x по к независимым измерениям °2(mean(x, к)) = o2(x)/ к, сразу получаем

Kk q , n ) ( P f ) = E < g F,> 5 , / ( 5 ° ² ) =

= E (°2/ 5)5/ (5°2 ) = i=1,.., n

= (1/ 5 ) E 1 = n / 5 = K M ( I , P f ) . i = I ', n n

При этом несколько непривычно и неудобно то, что K M ² ( I, P F ) уменьшается с ростом степени упрощения, а также то, что его значение зависит от площади кадра (на самом деле – от числа пикселов в базовом разбиении I ). Чтобы этого избежать, перейдем к нормированному значению. Поскольку наиболее сильным упростителем среди всех мозаичных пытьевских проекторов является, очевидно, проектор на простейшую форму P O , имеет смысл нормировать K M ² ( I, F )= K M ² ( I, P F ) по значению K M ² ( I, O )= K M ² ( I, P O ). При этом, поскольку K _M ² ( I, O ) — K _M ² ( I, F ), нормированный морфологический показатель степени упрощения ( МПСУ ) для оператора P F принимает вид:

К м ( I , о ) ( P f ) = K M ( I , P o ) / K M ( I , P f ) = 1/ n ,      (21)

и теперь, как легко увидеть,

^K M ( I , о ) ( P I ) — ^K M ( I , O ) ( P F ) — ^K M ( I , O ) ( P O ) = ¹ .      ⁽²²⁾

Таким образом, с ростом числа областей разбиения, в которых при фильтрации P F производится усреднение значений яркости, сила фильтрации (степень сглаживания) падает.

Выше мы отмечали, что оценки сложности должны монотонно изменяться при таких последовательных преобразованиях образа, при которых число его элементов увеличивается, и монотонно уменьшается при таких последовательных преобразованиях образа, при которых число его элементов уменьшается. Для мозаичных форм это операции слияния и разбиения областей. Таким образом, характеристика K M ( I,O ) ( P F ), описывающая оператор P F , связанный с мозаичной формой F , оказывается полностью согласована с оценкой сложности мозаичной формы F . Чем проще форма, тем сильнее сглаживает фильтр.

Исходя из этого, мы можем определить операторную меру сложности формы F как

^Q M ( I , O ) ( P F ) = exp ( 1 ^{— K} M ( I , O ) ( P F ) ) .               ⁽²³⁾

Нормировочное преобразование exp (1 – x) здесь потребовалось, чтобы обеспечить условия нормировки Qm(i,o)(Pf) e[0,1] и нулевой сложности простейшего образа QM(I,O) (PO) =0. Условие монотонности в цепочках преобразований слияния / разбиения соблю- дается в (23), как и в базовом (21), ввиду монотонности нормировочного преобразования.

Сравнение различных мозаичных операторов по средней степени упрощения.

Статистически упрощающие фильтры

Перейдем теперь к другим мозаичным операторам, которые не являются стандартными пытьевски-ми проекторами.

Известно, что пытьевский проектор P ( g,F ) имеет математическую форму усреднения (mean) по области:

g F ⁽ x , y ) = P _g , f ) g ⁽ x , y ) =

= E mean (g(x, У), Fi )xr(x, У), i=1,^, n потому что он является решением минимизации L2 нормы отклонения проекции от проецируемого изображения

E(g,F) = min(gF e F)||g(x, У) - gF(x, У)||2L2, которая, в свою очередь, определяется статистической моделью наблюдения P( f | F ) =P( f | fF) P( fF | F) вида:

f (x, У) = fF (x, У) + N(0, °), где N(0, °) - гауссовское случайное аддитивное отклонение; P (fF | F) = 1, если fF eF. В связи с этим, поскольку модель наблюдения мы не рассматриваем как часть морфологической модели Mf, нам следует считать эту модель (точнее, обусловленную ей процедуру фильтрации по заданной модели) частью морфологического оператора. Соответственно мы можем обозначить пытьевский оператор PF как P(g,F,mean).

Если мы зададим иную модель наблюдения P ( f | f F ), это приведет другому мозаичному морфологическому оператору для той же модели:

P (g , F ,proc) :P( g I F ) =

= ^{P ( g 1 g} ( g , F ,proc) ) ^{P ( g} ( g , F ,proc) ^{1 F} ) =

= ^P ( g ^{1 P} ( g , F.proc ) g ) ^ m^ax( РГОС ),                ⁽²⁴⁾

g ( g , F , proc ) ⁽ x , У ) = P(g , F , proc ) g ⁽ x , У ) =

= E p^roc ( g ^{( x} , у ), ^F i ) x f ⁽ x , у ). i =1,^, n

В частности, если некоррелированный аддитивный шум импульсный или характеристики его вообще неизвестны, наилучшим оператором оценки (фильтрации) значений яркости будет медиана по области, которая, как известно, минимизирует сумму модулей отклонений, т.е. L 1-норму, выбирая значения из имеющегося вариационного ряда наблюдений яркости, что соответствует решению дискретной оптимизационной задачи (задачи с ограничениями по выбору значений):

II g ⁽ x , У ) - g F ⁽ x , У )| L 1 ^ ^ min ( g F ⁽ x , y ) е ^F , g Fi е { g Gj } _{у = 1}, ^g ( g , F , med ) ⁽ x , y ) = ^P (g , F , med ) ^{g (} x , y ) = = Z med ( g ( x , y ), F ) x F ( x , y ).

i =1, n , n

Если аддитивный шум униполярный, наилучшими операторами оценки (фильтрации) значений яркости (в зависимости от знака) будут P ( g,F, min) и P ( g,F, max) , вычисляющие минимум или максимум по области, что соответствует решению оптимизационных задач с монотонными ограничениями, и т.д.

Попробуем при помощи введенного нами МПСУ (21) количественно оценить степень упрощения для мозаичного медианного фильтра P ( g,F, med) . По аналогии с (20) запишем:

KM( Q, I) ( P( g, F, med) ) = ( ||g (g, F, med) || / Д||g||/ , (26) \ / g c I \ / g c I откуда, с учетом известной оценки дисперсии выборочной медианы нормально распределенной величи ны x по к независимым измерениям (при к >> 1)

g2 (med(x, к)) = (п / 2)g2 (x) / к, получаем:

K M(Q , I ) ( P g , F , med ) ) = Z ( g ^ ) S / ( S g ) = i =1,.., n

= Z (п/2)(g2/Si)Si/(Sg2) = i =1,.., n

= ( П /2) n / S = ( П /2) K M ( I , P (g,F , mean ) ) .

Отсюда

K M ( I , O ) ^{( P} (g , F , med ) ) =

= K M ( I , ^P (g , O , mean ) ) / K M (Q , I ) ( ^P (g , F , med ) ) = = ^{(2/ п )} K M ( I , O ) ( P (g , f , mean ) ) .

Таким образом, в рамках данной вероятностной модели формы I c независимыми нормально распределенными яркостями всех пикселов изображения фильтр P ( g,F, med) в среднем упрощает в п /2 ® 1,57 раз слабее, чем P ( _g,_F, _mean) . Это естественно, т.к. выборочное среднее является оптимальной оценкой среднего в нормальном распределении (именно поэтому мы рассматриваем в качестве «пробного камня» самый сильный упроститель P ( _g,_O, _mean) , а не более слабый P ( _g,o, _med) ). Следует только помнить, что при другой вероятностной модели распределения яркости пикселов результат сравнения по силе упрощения фильтров P ( g,F, med) и P ( g,F, mean) может оказаться иным.

Заметим, что выражение (28), насколько нам известно, впервые вводит единую унифицированную характеристику для сравнения различных по типу (линейных и нелинейных) морфологических операторов.

Интересно также то, что из прямой пропорциональности K m ( i,o ) ( P ( g,F, med) ) и K M ( I,O ) ( P ( g,F, mean) ) непосредственно следует, что для множества медианных фильтров с мозаичными формами F и G справедливы те же отношения сравнения по сложности, что и для множества линейных проекторов Пытьева с теми же мозаичными формами. В частности, для них справедливо показанное выше свойство монотонности: чем проще форма F , тем сильнее упрощает фильтр P ( g,F, med) .

Необходимо отметить, что статистическая оценка степени упрощения оператора на основе усреднения его действия по выбранной тестовой форме вида

KM( Q, I) ( P g) ) = ( ||P( g) g(x, У Л /(||g(x, У )||2) , g c I                 g c I вообще говоря, может быть определена для любого оператора P(g). Даже если такую характеристику нельзя получить аналитически, ее всегда можно оценить методом Монте-Карло.

Если при этом K _M ( q , I )² ( P ( _g ) ) <  1, то исследуемый оператор P ( g ) можно считать упрощающим (неусложняющим) в статистическом смысле. Это более слабое определение, чем строгое требование неусложнения любого возможного изображения. Например, мозаичная медиана, как мы показали только что, является упрощающим фильтром в статистическом смысле. Но легко убедиться, что она не является упрощающей в строгом смысле (в некоторых случаях норма изображения после медианной фильтрации растет!). Такую статистическую УМ-морфологию (морфологию статистических УМ-фильтров) можно считать корректным расширением строгой УМ-морфологии, поскольку все строгие УМ-фильтры, очевидно, являются также и статистическими УМ-фильтрами.

Морфологическая корреляция мозаичной формы и диффузного мозаичного оператора.

Показатель силы упрощения оператора в диффузных мозаичных морфологиях

Рассмотрим теперь в том же ключе диффузные мозаичные фильтры [8, 9], соответствующие нечетким реляционным формам.

Пусть имеются четкая мозаичная форма F и нечеткая мозаичная форма G с мозаичными формами F и G соответственно. Для четких мозаичных форм F и G можно записать:

f(x,y) = Z fiхFi(x,y);g(x,y) = Z gjXG(x,У), i=1,^, n                                  j=1,^, m h f II2 = Z f2Si,||fGl2 = Z fjSGj. i=1,^, n                  j=1,^, m

Теперь мы запишем для нечеткой формы G:

f 31 = Z f ( Sil / SGl ), i=1,^, n

fj = Z Y Gjf = Z Y Gjl Z f (Sil / Sgi ) = l=1,—, m       i=1,—, n

g ⁽ x , y ) = Z g Ij X Ij⁽ x ’ y ), j =1,—, S

= Z f Z (YGjlSil ) / SGl = Z вGjifi ’ i=1,—, n    l=1,—, m                            i=1,—, n где

P Gji = Z ( ^Y Gjl S il ) / ^S Gl ’ l =1,—, m

^Y Gjl = ^b Gjl ^S Gj / Z ^b Gjt ^S Gt , t =1,—, m

{ b cji } - элементы реляционной модели G .

Пусть вновь справедливы те же предположения о плотностях распределении значений яркости fu-f n . Тогда по аналогии с (12) мы можем определить среднеквадратичный эффективный коэффициент морфологической корреляции (СКМК) формы F и диффузного мозаичного фильтра P _G как

KM(F,G) = (If||2)/(|| f ||2).

Подставляя соответствующие выражения, получаем:

KM (F, Pg ) = с2 Z Z вG2SG / (^S) = j=1,—, m i=1,—, n

= Z P Gj Z в Gji ².

j =1,—, m      i =1,—, n

Заметим, что в частном случае, когда форма G является четкой формой, т.е.

bj = {1: j = l ;0: j * l}, yGjl = {1: j = l ;0: j * l}, вGji = Z (YGjlSil ) / SGl = Sij / SGj = pij / pGj .

l =1,—, m

Отсюда

K M ( F , P g ) = Z p Gj Z ( j ^p4 = j =1,..., m       i =1,..., m

= Z Z p-2/pGj = KM(F,G), j=1,...,m i=1,—,n т.е. МКК четких форм (12) является частным случаем МКК четкой формы и нечеткого оператора (29).

Рассмотрим теперь случай диффузной фильтрации оператором P F сложнейшей формы I (пиксельного разбиения). В этом случае выражение (29) принимает форму

^K M ( I , P F ) = Z p Fi Z ^e Fji .

i =1,—, n     j =1,—, S

Удобно рассмотреть задачу оценки K m ² ( I, P f ) для нечетких операторов в форме взаимной модели. Очевидно, I имеет здесь базовую (по топологии) форму I = F л I , состоящую из набора областей парных пересечений { I j = F i n I } i=i_i.„ n; j=i_i.„ s . С ее помощью для изображений g е I, f е F

f ⁽ x , y ) = Z f i x f-⁽ x , y ) = Z Z ^fF S ij X ij⁽. x , y );

i =1,—, n                       j=1,—, Si=1,—, n структурные представления моделей Mg и Mf могут быть представлены в виде взаимных морфологических мозаичных моделей Mg i=MgI и Mf|I=MfI. В форме взаимного реляционного представления запишем:

GgI = Ш Ij = Ы X’ y X1)}

-   l> j =1,—,

К r>= j, j ,1 )j„S,=1S bfli = {1: j = l;0: j * l}, j = 1,..,S;l = 1,..,S , q^ ={gIJ = gl:j = l;0: j * l}, j = 1, —,S;l = 1, —,S.

G fI =({( I j =X y⁽ x , y ⁾,¹ )} _j =₁, _— , _S ,

^{(r ^IFj = bb_1Fjl , q I^Fjl p)}

'                                                                 ' I ^^X , • • .,и ; I ^^X ,. . ,U .

) ^b IFjl — Z Z ^b Fik ^S ij^Skl } r

[            ⁱ = ¹ ,^, ^nk =1,.., nj =1,.., s . l =1,—, s

Sij = -{1, Fi n Ij ;0 - в противном случае} bIFjl = bIlj е[0,1],| biijj- bIFjl },-, ,.,, c, v                       v j =1,.—, S ; l =1,... S bFik = bFkl е[0,1],{ bFii — bFik } - .         ,

X                      -* i =1,., n ; k =1,.. n , qIFjl =) fIFj = Z fFiSjj : j = l;0: j * l [           i=1,—, n j = 1, —, S; l = 1, —, S.

Оператор P _F диффузной фильтрации изображения g еI по нечеткой модели формы F имеет вид:

gF(х, y) = PFg(X, y) = Z gIFjXIj(x, у), j=1,—,S gIFj = Z в IFjlgn ’ j = 1’ — ’ S ’ l=1,—, S eiFj l = biFji / Z bifj q .

q =1,—, S

Отсюда

IIgI|r = Z g2’ j=1,—, S

r              ^2

IIgF|l = Z gIFj = Z I Z вIFjlgIl I .

j =1,—, S          j =1,—, S \ l =1,—, S           )

Примем те же предположения о плотностях распределении значений яркости g _I1 , ._ , g _IS : ( gy ) = 0, ( gyg _Il ) = { с ² , если j = l ; 0 - в противном случае}, где с -дисперсия распределения p ( g y).

С учетом введенных предположений и обозначений средний квадрат нормы изображения g формы I имеет вид:

(IIgI|I") = с2S .

Средний квадрат нормы отфильтрованного изображения g F :

( Г

I S ^P IFjl g ll I

^ j =1,., S         )

= S I S PlFjl gn    S P IFjtgIt I = j=1,.,S \\l=1,.,S J\t=1,.,s          )/

= S S S pifipiFtkgiigi^ = j=1,., S l=1,..., St=1,..., s

= S S P?Fji°2 = °2 S S PF ■ j=1,., Sl=I,., S                  j=I,., Sl=1,., S

Подставляя соответствующие выражения, получаем:

KM (I, Pg ) = °2 S S PIFjl2/ (°2S) = j=1,., Sl=1,., S

= (1/S) S S P IFjl 2- j=1,., Sl=1,., S

По аналогии с (21) нормированный морфологический показатель степени упрощения (МПСУ) для нечеткого оператора P f = P ( g,_F P ) принимает вид:

K M ( I , O ) ^{( P} (g , F ,P) ) =

= K M ( I , P (g , о , mean ) ) / K M ( I , P g , F ,P) ) =                (32)

=1/ S S P2FV, j=I,., Sl=I,., S или в непрерывной форме

K m ( I , о ) ( P g , f ,p) ) = 1/£ £ P F ( x , У , u , v ) dxdydudv ,(33)

где p F(x,y,u,v) - диффузное ядро оператора P (g,F, p ) , связанное с реляционной моделью b _F(_x,_y,u,v) формулой вероятностной нормировки:

P _F ( x , y , u , v ) = b_F ( x , y , u , v )/Ц_л b_F ( x , y , a , b ) dadb .

Смысл выражения (33) становится наиболее ясен в форме

K M,O , ( P g « ) = 1/| p _F ( x , y , u , v )[₂ .               (34)

Заметим, что, как мы показали выше, в случае четкой мозаичной формы

||P f (x, y , u , v )||2 2 = n , где n - число областей разбиения формы F. Т.е. квадрат нормы ядра диффузного оператора как показатель силы упрощения является аналогом числа областей разбиения базовой формы пытьевского мозаичного проектора.

Связь сложности формы и степени модификации в диффузных мозаичных морфологиях

Выше мы показали, что для четких мозаичных форм справедливо утверждение, связывающее упорядоченность форм по сложности и силу модификации соответствующих проекторов:

F с G о b_F ( x , y , u , v ) >

> ^b G ⁽ x , y , u , v ) ^ K M ( I , O ) ( P F ) >  K M ( I , O ) ( P G ) .

Иными словами, если в форме F некоторые пикселы дополнительно связаны между собой отношением «равны по яркости» по сравнению с формой G , то и соответствующий фильтр P F упрощает сильнее, чем P _G . Отсюда мы имеем для четких форм:

b_F ( x , y , u , v ) >  b_G ( x , y , u , v ) о

^ |^p f ⁽ x , y , u , v )|| ² 2 < ||^P G ⁽ x , y , u , v ⁾|| ² 2 .

Логично было бы предположить, что такое же соотношение имеет место и для нечетких форм. Однако это необходимо проверить.

Рассмотрим задачу в следующем простейшем виде. Пусть имеются две нечеткие формы G fI_F и G _gIG с реляционными моделями сходства пикселов соответственно

^{{ b} I^Fjl ^} j =1, S ; l =1,.., S ’ ^b I^Fjl = ^b I^Fj ^{G [0}’¹]’ ^{ b F ^— b j } j =1,_ S ; l = 1 . ,S

^P IFjl = b IFjl / S ^b IFjq , ^j = 1, . , ^S ; l = 1,..., ^S , q =1,., S

^{ b IGjl } j =1,..., S ; l =1,.., S ’ b IGjl = b G *' I⁰"¹!" ^ ^{b IF}j ^— b j ^} j =1,. s ; l =1,.., S

IGjq , j =1,.., S ; l =1,.., S .

^P IGjl = b IGjl / S ^b q =1,., S

Аналогом гипотезы (34) в такой дискретной модели будет утверждение

{bIFij > bIGj }j=1,.,S.l=1,.,S ^ S S PF < j=1,., Sl=1,., S

< S S P 2Gl ^ S S ( P ? Gjl -P ? Fjl ) > 0. j =1,., S l =1,., S             j =1,., S l =1,., S

Рассмотрим простейший частный случай, когда модели связи пикселов bIF и bIG совпадают всюду, кроме пары пикселов под номерами r и t, причем, естественно, r * t, bIFrt = b1Flr = f > bIGrt = bGr = g .

Очевидно, это несовпадение приведет к несовпадению только r -й и t -й строк нормированных по строкам матриц P _IFj_l и P IGj . Соответственно условие (26) принимает вид:

Г

2 S (PIGjr  P Fjr)>0 О| S P2Gjr > S P 2Fjr ^S I b IGrj / S bIGrq j=1,...,S                                  j=1,.,S           j=1,.,S             j=1,.,S ^         q=1,.,S)

> S I ^b IFrj / S ^b IFrq j =1,., S (         q =1,., S

Г -    ) Г „    У  Г -   ) Г -)

^ I S ^b IGri I / 1 S b IGrq I > I S b IFrj I / 1 S b IFrq I

( j=1,.,S      )  ( q=1,., S       )     (j=1,.,S      )  ( q =1,., S)

Обозначим дополнительно

^Y = ^ ^b№rq = ^ q _' bto rq , Y >  1 q * t

( из условия b_IFrr = 1 ) ,

X = £ b iFrq = E b iGrq , X >  Y >  1 q * t            q * t

(из условия b_IFrr e [0,1] ) ,

( Y + g ² ) /( X + g ) 2 >  ( Y + f 2 )/( X + f ) 2 О

o ( Y + g ² ) ( X + f )² >  ( Y + f ²)( X + g )² О

o( Y + g2)(X2 + 2 Xf + f2 )>

• >    ( Y + f ²) ( X ² + 2 Xg + g ² ) o

О YX ² + 2YXf + Yf ² + g ² X ² + 2 Xg ² f + g ² f ² >

• >    YX ² + 2 YXg + Yg ² + f ² X ² + 2 Xf ² g + f ² g ² О

О ( f - g )(2 YX + Y ( f + g ) -

• - X ²( f + g ) - 2 Xfg ) >  0 о ( f = g )

или

(2 YX + Y ( f + g ) - X ²( f + g ) - 2 Xfg >  0) о ( f = g )

или

( 2 X ( Y - fg ) + ( Y - X ² ) ( f + g ) >  0 ) .            (37)

Заметим, что если условие (37) окажется тождественно истинным, то тем самым мы докажем справедливость (36) не только в частном, но и в общем случае (по индукции), поскольку между любыми двумя реляционными моделями всегда можно выстроить непрерывную цепочку нечетких форм, в которых значения отличаются лишь в одном пикселе. И наоборот, если удастся опровергнуть (37), то и (36) автоматически будет опровергнуто.

Проверим полученное нами условие (37) на соответствие ранее выявленному факту, что для четких форм это условие всегда должно выполняться. Если формы F и G четкие, то ( f = g) или (( f = 1) и ( g = 0)), иб кроме того, X = Y, поскольку bIFrq e {0,1} О bIFrq = b№rq О X = Y ■

Отсюда (37) принимает вид

• 2    XY + Y - X ² >  0 О X ² + X >  0,

что всегда верно, ведь X > 0. Таким образом, мы подтвердили прежний вывод относительно согласованности по сложности четких форм и мозаичных проекторов.

Вернемся к общему случаю диффузных операторов. Пусть заданы некоторые значения X, Y, f . Определим такое критическое значение g *, для которого

• ²    X ( Y - fg * ) + ( Y - X ² )( f + g * ) = 0            ₍₃8)

О g * = ( 2 XY - f ( X ² - Y ) ) / ( 2 Xf + ( X ² - Y ) ) . ( )

Если существует такой набор { X, Y, f }, для которого критическое значение g * e (0, f ), значит, гипотеза (36) неверна. Выберем, например, вариант

• { X = 2 Y , f = 1} ^

^ g* = (2XY - f (X2 - Y)) / (2Xf + (X2 - Y)) =

= ( 2(2 Y ) Y - ( (2 Y )² - Y ) ) / ( 2(2 Y ) + ( (2 Y )² - Y ) ) =

= ( 4Y2 - 4Y2 + Y) / (4Y + 4Y2 - Y) =

= 1/(3 + 4 Y ) <  1 = f .

Поскольку для любого Y> 1: g*e (0, f), мы доказали, что гипотеза (36) неверна, т.е. степень упрощения МПСУ для нечетких операторов P(g,F,в), P(g,G,в) не связана с отношением сложности bF(x,y,u,v) > bG(x,y,u,v), и, соответственно, меры сложности цH (bF ) = ||bF (x, y, u, v)||£ 1,

Ц L 2 ( в F ) = ||P F ( x , У , u , v )|| L ₂

также между собой не согласованы. С точки зрения привычной логики оценки сложности мозаичных четких форм это очень странный результат:

– в четких формах и соответствующих проекторах, если мы усиливаем связь между пикселами в модели, то усиливается и степень сглаживания оператором по такой модели, а если ослабляем, то и сглаживание будет слабее;

– но в нечетких формах и соответствующих диффузных фильтрах это бывает не так: иногда связь между простотой формы и силой сглаживания прямая, а иногда обратная, т.е. порой мы ослабляем связь между пикселами в модели, а сглаживание усиливается.

Еще удивительнее такое отсутствие связи между характеристиками модели и поведением оператора выглядит, если вспомнить, что для четких форм и проекторов ц _L2 ( в F) = n ■ Тогда получается, что в нечетких формах n может как бы расти (снижение средней связанности пикселов – аналог разбиения областей), но фильтр при этом будет упрощать (сглаживать) изображение не слабее, а сильнее.

Эта качественная разница в связи между реляционными и операторными моделями для диффузных и проективных мозаичных линейных фильтров, по-видимому, указывает на то, что для нечетких форм интерпретация только через связи между пикселами уже не является вполне адекватной. Поскольку пикселы имеют теперь не только полную (1) или отсутствующую (0) связь, такая модель с разной силой связи ([0,1]) между пикселами уже указывает не только на степень их сходства, но и на степень их различия. Косвенным свидетельством этого является то, что собственные функции произвольных диффузных операторов не похожи по виду на характеристические функции областей – они имеют положительные и отрицательные рецептивные поля.

Заключение

В данной работе на основе концепции УМ-морфологии рассмотрена задача сравнения статистических оценок свойств различных морфологических фильтров, построенных на основе мозаичных моделей изображений.

В качестве численных статистических оценок введены морфологический коэффициент степени модификации и морфологический коэффициент степени упрощения.

Исследована связь меры сложности, меры простоты и степени модификации в морфологии Пытьева. Показано, что мера ОГО-сложности µ H ( F ) непосредственно связана с мерой простоты K M ² ( F, O ). Эта связь является подтверждением внутреннего единства морфологического анализа Пытьева во всех его формах – атрибутной, реляционной, метрической и операторной. Она также демонстрирует внутреннюю связь между морфологическими инструментами сравнения по сходству / различию и сравнения по сложности. В частности, теперь установлена связь ОГО-метрики не только с мозаичным и реляционным представлениями мозаичных форм, но и с морфологическим проектором Пытьева, что до сих пор было совершенно неочевидно.

На основе среднеквадратичного морфологического коэффициента корреляции введен нормированный морфологический показатель степени упрощения. Для данного показателя подтверждено, что чем проще мозаичная форма, тем сильнее сглаживает соответствующий пытьевский проектор. Иными словами, в рамках четких пытьевских форм, если мы усиливаем связь между пикселами в модели, то усиливается и степень сглаживания оператором по такой модели, а если ослабляем, то и сглаживание будет слабее.

На примере усредняющего и медианного мозаичных фильтров рассмотрена задача сравнения различных мозаичных операторов по средней степени упрощения. Показано, в рамках вероятностной модели формы I c независимыми нормально распределенными яркостями всех пикселов изображения фильтр P (g,F, med ) в среднем упрощает в π /2 ≈ 1,57 раз слабее, чем P ( g,F, mean) . На примере мозаичной медианы в качестве обобщения введено понятие УМ-операторов, упрощающих (неусложняющих) в статистическом смысле. Это более слабое определение, чем строгое требование неусложнения любого возможного изображения. Статистическую УМ-морфологию (морфологию статистических УМ-фильтров) можно считать корректным расширением строгой УМ-морфологии, поскольку все строгие УМ-фильтры, очевидно, являются также и статистическими УМ-фильтрами.

Рассмотрена морфологическая корреляция мозаичной формы и диффузного мозаичного оператора. В качестве показателя силы упрощения оператора в диффузных мозаичных морфологиях предложено использовать квадрат нормы ядра диффузного оператора, являющийся аналогом числа областей разбиения базовой формы пытьевского мозаичного проектора.

Исследована связь сложности формы и степени модификации в диффузных мозаичных морфологиях. Доказано, что гипотеза о наличии такой связи неверна, т.е. степень упрощения МПСУ для нечетких операторов не связана с отношением сложности для соответствующих ядер: связь между простотой формы и силой сглаживания фильтра может быть как прямой, так и обратной. Эта качественная разница в связи между реляционными и операторными моделями для диффузных и проективных мозаичных линейных фильтров, по-видимому, указывает на то, что для нечетких форм необходима разработка более адекватных оценок сложности. Это должно стать предметом дальнейших исследований в данном направлении.

Работа выполнена при поддержке гранта Российского научного фонда № 16-11-00082.