Сравнение свойств гипергеометрических мод и мод Бесселя

Особый интерес в практическом использовании имеют лазерные пучки, обладающие небольшой дифракционной расходимостью, так как сохраняют высокую осевую концентрацию энергии на больших расстояниях. К таким пучкам относятся моды Бесселя [1] и гипергеометрические (ГГ) моды [2-4]. Последние имеют наименьшую расходимость среди известных параксиальных мод лазерного излучения. Распределение интенсивности в поперечном сечении таких пучков похоже на распределение интенсивности для мод Бесселя и представляет собой набор концентрических чередующихся светлых и темных колец. При этом в отличие от бесселевых мод гипергеометрические моды обладают одной особенностью: пространственная частота картины дифракции асимптотически стремиться к бесконечности. Известно так же, что для ограниченных ГГ-пучков, так же как и для Бесселевых, существует некоторое предельное значение расстояния, на котором пучок сохраняет свои модовые свойства.

1. Решение уравнения Шредингера

Параксиальное волновое уравнение в цилиндрических координатах (уравнение типа Шредингера) имеет вид:

2 ik — ■     ■--+          E ( r , ф , z ) = 0,    (1)

(    a z a? rdr ? аф² J

где n > 0 - целое число, y - комплексное число; данные числа в дальнейшем будем называть параметрами ГГ-мод; w – вещественный параметр, задающий масштаб ГГ моды, аналогичен радиусу перетяжки Гауссового пучка (в данной статье будут рассмотрены пучки для которых w =1); Г( x ) – гамма функция и ₁ F ₁( a, b, x ) – вырожденная (или конфлюэнтная) гипергеометрическая функция, которые были описаны ранее в работах [4, 5].

При этом на нулевом расстоянии вдоль оптической оси, при z = 0 выражение (3) имеет вид:

.     1 Г w)

En Y (r, ф) =7-1 - I eXP 2п V r )

x exp( in ф ),

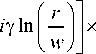
Существует сходное семейство решений дифференциального уравнения (1) в системе координат с неполным разделением переменных:

x = rz cos ф , y = rz sin ф , z = z .

Они являются линейно-независимыми параксиальными модами Бесселя [6]:

E n , r ₀ ( r , ф , z ) = ( - i ) ^{n + 1}

ro k x

2n z

где ( r, ф ) - поперечные полярные координаты, z - координата, направленная вдоль оптической оси, k= 2 n!X - волновое число света с длинной волны X . Решая (1) в цилиндрической системе координат вида:

x

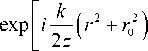
Jn I —0 I exp(inф) V z I

x = r V z cos ф,

■ y = r V z sin ф,

получаем решения в виде ортонормированного базиса, называемые Гипергеометрическими модами [5]:

/ х           2 x n /2

_ ( Л 1 Г 2 Z ) ² Г kr ² )

En_л ^{( r} , ф , ^z ) = —I 7-Т I И-1 ^x

2 п n ! V kw ) I 2 z I

exp i 4 ( n - i y + 1) Г

n + i y + 1 )

-------- x

2     )

Г n - i у + 1

1Л “г-

, 1 ikr ² ) a

, n +1,—— I exp( in ф ), 2 z I

где Jn ( x ) – функция Бесселя n -го порядка, r 0 – вещественное число.

Такой бесселевый пучок дифрагирует (расходится) по мере распространения вдоль оси z и обычно формируется с помощью узкой кольцевой диафрагмы в непрозрачном экране [7].

В данной работе проводится сравнение пучка (6) с пучком, который будет распространяться при формировании во входной плоскости (при z = 0) ограниченного апертурой распределения:

E n , a ( r , ф ) = J n ( a r ) exp( in ф ). (7)

В [6] было показано, что бесконечный непараксиальный бесселевый пучок, имеющий распределение (7) во входной плоскости, после преобразования Френеля остается непараксиальным (не расходящимся), однако как будет вести себя ограниченный пучок (7), формируемый, например, с исполь-

зованием дифракционного оптического элемента, исследовано не было.

Распространение ограниченных апертурой пучков (4) и (7) моделировалось с помощью преобразования Френеля:

E ⁽ x , y , z ) = k. ^X

2n iz да да          c .1л

XJ J exp12^[(x-У2 +(y-n)2Ъх

-да -да       I)

2. Численное моделирование

В данном разделе проводится сравнение четырех типов пучков: аналитических ГГ и бесселевых мод (в соответствии с формулами (3) и (6), и их ограниченных аналогов по расходимости пучков, спектру пространственной частоты картины дифракции, сохранению модовых свойств, устойчивости к экранированию.

ГГ-моды были выбраны с параметрами n = 4, Y = -10, а бесселевы моды с параметрами n = 4, и различными а . Параметр масштабирования а подбирался путем совмещения центральных колец пучков на некотором расстоянии z :

kr

а = —

z

.

Для ограниченного Бесселевого пучка было выбрано а = 32 (значение, полученное при z = 100 мм ).

На рис. 1 приведены рассматриваемые типы пучков с длинной волны X = 633 нм , размером 2х2 мм и дискретизацией 1024 x 1024 отсчетов, на расстоянии z = 100 мм . Из рисунка видно, что искажения, возникающие из-за ограничения апертурой, сказываются на бесселевых пучках сильнее, чем на ГГ-модах.

Большой интерес также вызывает расходимость пучков. Ранее было показано [3], что ГГ-моды расходятся медленнее параксиальных бесселевых пучков (6). Для того чтобы проверить, как соотносятся расходимости ограниченных пучков (4) и (7), были проведены численные эксперименты. Расходимость отслеживалась по увеличению радиуса первого кольца в зависимости от пройденного расстояния z . Полученные зависимости представлены на рис. 2. Расходимость ограниченной ГГ-моды очень близка к своему аналитическому виду и действительно расходится до некоторого расстояния ( z = 250 мм ), т. е. ведет себя как непараксиальный пучок, описанный в [6], однако из-за ограниченности, только на конечном отрезке.

Сравнивая интенсивность ГГ и Бесселевых мод в поперечном сечении (рис. 1), легко заметить умень- шающийся период осцилляций ГГ-моды, в отличие от Бесселевой моды. Более наглядно это видно на рис. 3, где приведены радиальные сечения распределения интенсивности как аналитических, так и ограниченных пучков.

Для более детального исследования этого факта была введена величина, характеризующая пространственную частоту картины дифракции:

N to = —, R

где N – число колец светового пучка, поместившихся в апертуру радиусом R.

Выражение (10) для множества всех значений радиуса пучка, не превышающих радиус апертуры, также можно назвать спектром пространственной частоты картины дифракции:

N to( r) = —, 0 < r < R .

r

Графики, полученные для (11) и представленные на рис. 4 показывают, что кольца Бесселевого пучка имеют постоянную, одинаковую ширину, а у гипергеометрических мод кольца постоянно сужаются, так как увеличивается частота картины дифракции. Это верно как для аналитических пучков, так и для их ограниченных аналогов.

Поскольку амплитуда (4) имеет особенность в нуле (неограниченно возрастает при r = 0), то сформировать такое распределение корректно невозможно, поэтому для моделирования используется также вырезание центральной области. На рис. 5 а показано радиальное распределение интенсивности (4) и отмечены ограничители R 1 и R 2 . Первый вырезает круг в центре, где интенсивность была устремлена в бесконечность. Второй является ограничителем апертурой или диафрагмой. При моделировании распространения (4) с помощью оператора Френеля (8) были получены дифракционные картины для различных ограничителей R 1 и R 2 . Они представлены на рис. 6. Было проведено их сравнение с аналитическим решением (3), график которого изображен на рис. 5 б , по среднеквадратичному отклонению (СКО):

5 =

Z ( I 0 ^{( r} ) ^- I ^{( r} ) ) 2

R 1 <  r <  R 2

I Z 1 0² ( r )

1          R ; <  r <  R 2

.

где I 0 ( r ) – интенсивность эталонного поля, вычисленная в данном случае с помощью (3); I ( r ) – интенсивность поля, полученная с помощью преобразования Френеля.

В табл. 1 приведены параметры R ₁ и R ₂ подобранные таким образом, чтобы СКО было минимальным для распределения интенсивности пучка на заданном расстоянии. Как видно из таблицы 1 с ростом расстояния СКО увеличивается.

Таблица 1. Подбор параметров R1 и R2

z, мм	R 1 , мм	R 2 , мм	5 , %
100	0,05	0,99	5,29
200	0,12	0,96	11,63
400	0,23	1,00	28,91

Из таблицы 1 также видна зависимость:

R ₁ ~ z .                                           (13)

В [2] было показано, что в связи с ограниченностью реально формируемых ГГ-пучков апертурой радиуса R 2 , их модовые свойства сохраняются только до расстояния:

R 2

ctg (y/ R 2 )

> z .

Так же известно [7], что для Бесселевых пучков справедлива аналогичная зависимость:

kR

—- >  z

a

т.е. пропорциональность расстояния «жизни» моды радиусу ограничивающей диафрагмы.

При этом имеется обратная зависимость от «масштаба» ГГ и Бесселевых мод - у и a . У Бесселевых мод, сформированных с помощью узкой кольцевой диафрагмы (6), этот масштаб зависит от пройденного расстояния, как показано в (9). И масштабное согласование пучка (6) с (7) возможно только при фиксированном расстоянии (рис. 7).

Исследования влияния радиуса диафрагмы (рис. 8) показали, что лучше всего оставлять целое число колец, поскольку остатки (обрезанные кольца) вносят сильные помехи в картину дифракции. Особенно хорошо это заметно на рис. 8 б , где минимумы графиков СКО приходятся как раз на нули рассматриваемой функции Бесселя. Так в частности, лучше установить размер диафрагмы R ₂ = 0,95 мм , а не R 2 = 1 мм , т. к. в этом случае умещается максимальное целое количество колец, как показано на рис. 7 а .

В этом состоит одно из специфических отличий бесселевых мод от гипергеометрических.

моды Бесселя

Амплитуда (инвертированная)

Фаза

Амплитуда (инвертированная)

Гипергеометрические моды

Фаза

Рис. 1. Примеры гипергеометрических мод и мод Бесселя на расстоянии z=100 мм

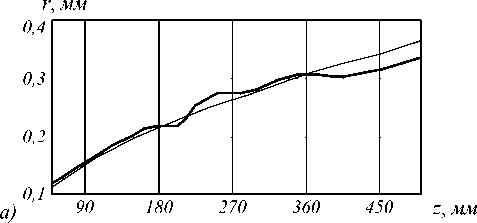
Рис. 2. Расходимость (а) гипергеометрической моды и (б) моды Бесселя на различных расстояниях z: аналитический пучок (тонкая линия), ограниченный апертурой пучок (жирная линия)

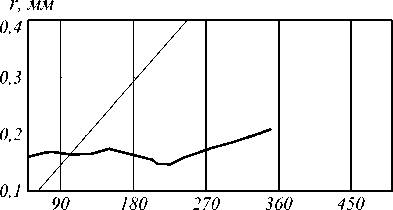
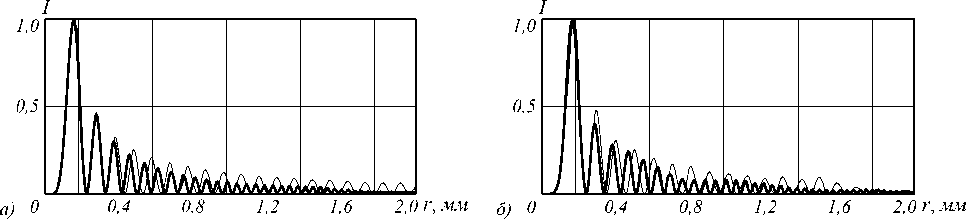
Рис. 3. Распределение интенсивности радиального сечения (а) бесконечного (б) ограниченного апертурой Бесселевого (тонкая линия) и ГГ (жирная линия) пучков

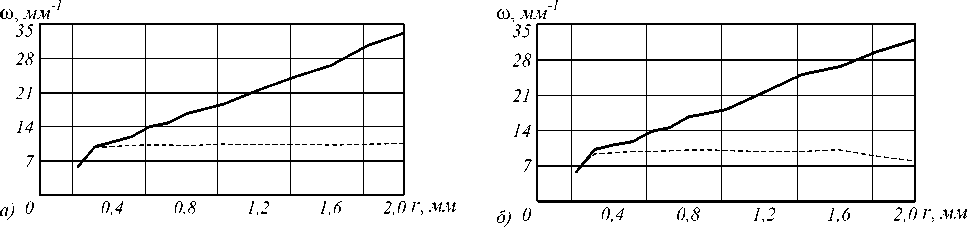
Рис. 4. Спектр пространственной частоты картины дифракции (а) бесконечного (б) ограниченного апертурой пучков:

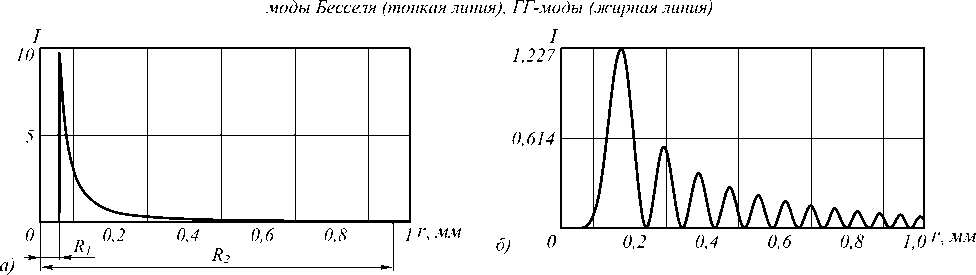
Рис. 5. Радиальное распределение интенсивности гипергеометрической моды (n = 4, γ = -10 ) при (а) z = 0 мм и (б) z = 100 мм (аналитический вид)

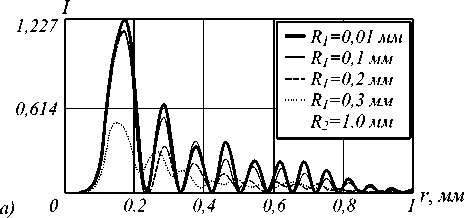
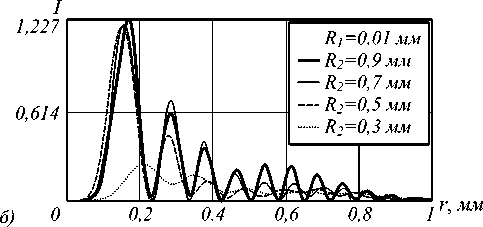
Рис. 6. Радиальное распределение интенсивности гипергеометрической моды рассчитанное с использованием преобразования Френеля при начальном распределении, показанном на рис. 5а, с апертурой, ограниченной радиусами R1 и R2 на расстоянии z = 100 мм: (а) варьируется радиус R1 и (б) варьируется радиус R2

I

0,16

I

0,08

О а)

0.2

0,4

0,6

R2=0.95 мм

0,8

r , мм ^,

б)    О

0,2      0,4      0,6      0,8

r , мм

Рис. 7. Радиальное распределение интенсивности Бесселевой моды для (а) выражения (7) (n=4; α =32) при z = 0 мм и (б) аналитического решения (6) (n=4; α =64) при z = 100 мм

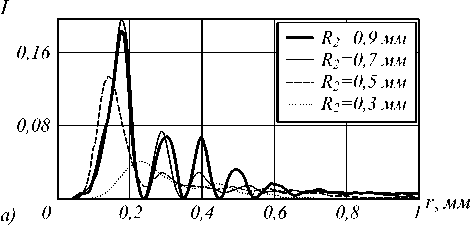
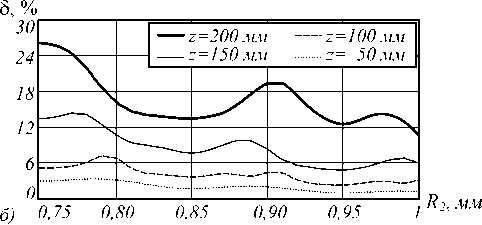
Рис. 8. Радиальное распределение интенсивности Бесселевой моды (n=4; α=32), полученное с помощью интеграла Френеля для апертуры, ограниченной радиусом R2, при z = 100 мм (а).

Зависимость среднеквадратичного отклонения полученного распределения интенсивности на различных расстояниях от исходного (7) в зависимости от радиуса апертуры R2 (б)

Дальнейшее сравнение ограниченных ГГ и Бесселевых мод сводилось к определению максимального расстояния, на котором сохранялись их модовые свойства. С этой точки зрения ГГ-моды показали лучшие результаты. При одинаковых R 2 = 0,95 мм и подобранных масштаба, таких что центральное кольцо было одинакового размера, ограниченная ГГ-мода отклонялась при распространении от своего аналитического вида гораздо медленней, чем бесселевый ограниченный пучок (рис. 9).

На рис. 10 можно сравнить распространение аналитических и ограниченных ГГ. Из рис. 10 б и рис. 11 видно, что ограниченный ГГ пучок разрушается постепенно, разглаживая дифракционные осцилляции по всему радиусу пучка равномерно.

Ограниченный бесселевый пучок разрушается постепенно с периферии от кольца к кольцу (рис. 12). Для установления данного факта при расчете СКО рассматривалась область, ограниченная N -м кольцом (рис. 13 а ).

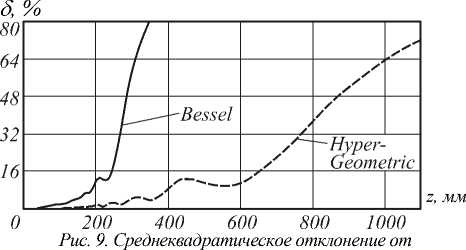
аналитического вида для ограниченной гипергеометрической моды (n=4; γ =-10) (тонкая линия) и моды Бесселя (n=4; α =32) (жирная линия) зависимости от z.

Далее было интересно выяснить, с какой скоростью разрушаются кольца. Для этого был установлен порог визуальной «разрушенности» кольца, которая наступает при достижении значения СКО δ = 20%. График зависимости разрушения колец (по номеру) от пройденного пучком расстояния приведен на рис. 13 б , он имеет линейный характер.

а)

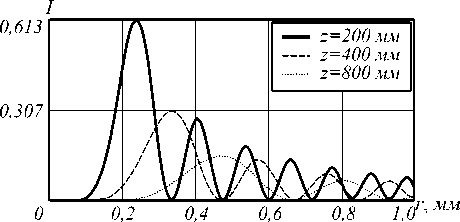
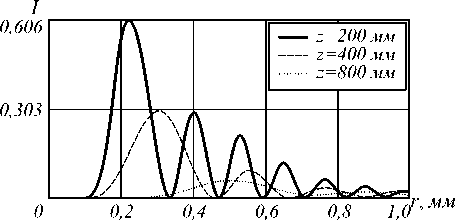
Рис. 10. Радиальное распределение интенсивности гипергеометрической моды (n=4; γ =-10) на различных расстояниях (а) для аналитического решения (3) и (б) при моделировании распространения пучка (7), ограниченной кольцевой апертурой с радиусами R₁=0,01 мм и R₂=1 мм

б)

Заключение

В заключении кратко сформулируем полученные результаты.

• •    Ограниченная ГГ-мода демонстрирует такую же расходимость, как и аналитическая – пропорционально z , однако ограниченный бес-селевый пучок имеет расходимость, среднюю между непараксиальным и параксиальным своим аналитическим решением.

• •    Проведенный анализ спектра частот поперечного распределения интенсивности показал, что, в отличие от Бесселевых, у ГГ-мод ширина колец сужается, линейно увеличивая свою пространственную частоту, с ростом радиуса пучка.

• •    Получены зависимости радиусов апертуры R 1 и

• R2 для ограниченных пучков ГГ-моды и R2 – бесселевой для формирования дифракционной картины на определенных расстояниях z с наименьшей погрешностью. Численно подтверждены зависимости (14), (15).

Рис. 11. Распределение инвертированной интенсивности гипергеометрического пучка на различных расстояниях z для кольцевой апертуры с радиусами R₁ = 0,01 мм R₂ = 1,0 мм .

z	25 мм	87 мм	152 мм	215 мм
N	8	6	4	2
к s л н о о к m S о к О н к К		^^^	^ ^Ё^ ^	о

δ , %

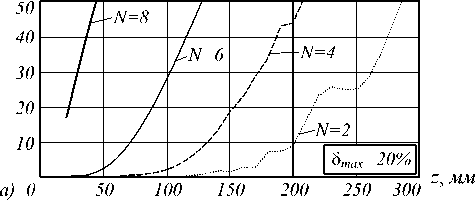
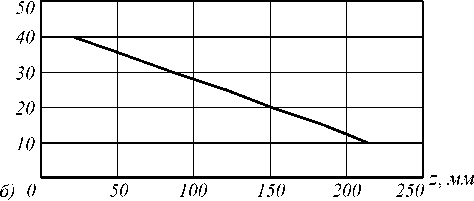
Рис. 13. Среднеквадратическое отклонение ограниченного Бесселевого пучка от идеального в области, ограниченной N-м кольцом на различных расстояниях z(а).

Зависимость количества не разрушенных колец бесселевого пучка N от пройденного им расстояния z(б)

Рис. 12. Распределение инвертированной интенсивности бесселевого пучка (с N уцелевшими кольцами) на различных расстояниях z для круглой апертуры радиуса R2 = 1,0 мм.

N

• •    Установлено, что ограниченная ГГ-мода сохра

няет свои свойства на расстоянии, которое примерно в 3 раза больше, чем расстояние, на котором сохраняет свои свойства ограниченный бес-селевый пучок, имеющий тот же масштаб.

• •    Кольца ограниченных бесселевых мод при распространении разрушаются постепенно от кольца к кольцу, начиная с крайнего, причем зависимость разрушения от расстояния z линейна. Ограниченная ГГ-мода разрушается по всему радиусу равномерно.

Работа выполнена при финансовой поддержке гранта РФФИ 07-07-97600.