Сравнение точных решений контактных задач для трансверсально изотропного полупространства

Введение. Пионером в области исследования трансверсально изотропных тел считается Эллиот [1, 2]. В контактных задачах теории упругости для трансверсально изотропного полупространства традиционно рассматривался случай, когда область контакта параллельна плоскостям изотропии [3, 4]. Случай, когда область контакта или трещины перпендикулярна плоскостям изотропии, назван «нетрадиционным» [5, 6]. В случае «нетрадиционной» ориентации плоскостей изотропии рассматривались задачи для полосовой, клиновидной, эллиптической и заранее неизвестной областей контакта [7–10].

Контактные задачи. Рассмотрим сперва «нетрадиционный» случай контактной задачи о вдавливании эллиптического в плане штампа в трансверсально изотропное полупространство x ≥ 0, граница которого перпендикулярна плоскостям изотропии z = const (на рис. 1 штамп вдавливается сбоку).

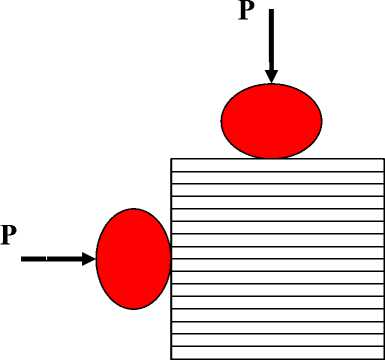
Рис. 1. «Традиционная» и «нетрадиционная» контактные задачи

Пусть основание штампа в области контакта описывается функцией f ( y, z ) =y+     .

2 R 2 R

Штамп вдавливается без перекоса центрально приложенной силой P , испытывая осадку δ . При заданной функции (1) и осадке δ требуется определить область контакта Ω , контактное давление q ( y , z ) в области Ω и силу P . На основании фундаментального решения [5] интегральное уравнение (ИУ) контактной задачи можно записать в форме

∫∫q(y0,z0)K(y-y0,z-z0)dy0dz0 =δ- f(y, z), (y,z)∈Ω,(2)

Ω

• 2 ∞∞

K ( y , z ) = ^{m 2   m 1 γ 3      ξ} ζ ζ exp( - iz ξ - iy η ) d ξ d η ,

4π2AD

D = m ₂ h ₁ ² ζ ₂ - m ₁ h ₂ ² ζ ₁ - 4( m ₂ - m ₁ ) η ² ζ ₁ ζ ₂ ζ ₃ ,

ζ n = Vγ ² n ξ ² +η ²  ( n = 1,2,3),   h l = ( m l + 1) γ 3 ² ξ ² + 2 η ²  ( l = 1,2).

Здесь величины γ n , m l зависят от упругих параметров A ij [5], γ , γ являются корнями уравнения

• γ ⁴ A ₁₁ A ₄₄ - γ ²[ A ₁₁ A ₃₃ - A ₁₃ ( A ₁₃ + 2 A ₄₄ )] + A ₃₃ A ₄₄ = 0,                                     (3)

2 A ₄₄          A ₁₁ γ ₁ ² - A ₄₄          A ₁₁ γ ² ₂ - A ₄₄

γ ₃ =      ,   m ₁ =               , m ₂ =               .

A ₆₆           A ₁₃ + A ₄₄            A ₁₃ + A ₄₄

Для случая (1) точное решение ИУ (2) имеет в вид [5]

Механика

yz

q(y,z)=q0  1-  2 -  2 , P= ba

∫∫ q ( y , z ) dydz = ^{2 π} abq ₀, Ω

(m1 -m2)γ32 2π      ζ1(θ)ζ2(θ) cos2θdθ q0     8A66     ∫ D(θ)[(a/b)2cos2θ +sin2θ]1/2, b 2    a 2         R1

+      = δ,       =

2R  2R      Rd

ⁿ       Z 1 ( 6 ) Z ₂( 9 )cos⁴ 9 d 9

^J D ( 9 )[( a / b )² cos² Q + sin² 9 ]^3/2 ’

ⁿ    Z 1 ( Q ) Z ₂( Q )cos² 9 sin² Q d Q

" ^J D ( 9 )[( a / b )²cos² 9 + sin² Q ]^3/2,

Z n ( 9 ) = Vy П cos² 9 + sin² 9 ( n = 1,2,3),

D ( 9 ) = m i h 2 ² ( 9 ) Z i ( 9 ) - m 2 hy ( 9 ) Z 2 ( 9 ) - 4( m i - m 2 ) sin² 9Z i ( 9 ) Z 2 ( 9 ) Z 3 ( 9 ),

h l ( 9 ) = ( m l + 1) y 2 cos² 9 + 2sin² 9 ( l = 1,2).

При заданных величинах δ , R 1 , R 2 отношение полуосей эллипса контакта a / b определяется из второго соотношения (6). Затем величина a находится из первой формулы (6), величина q 0 ― из (5). Вдавливающая сила рассчитывается по второй формуле (4).

В традиционном (классическом) случае контактной задачи для трансверсально изотропного полупространства (на рис. 1 штамп вдавливается сверху) ИУ контактной задачи имеет вид (формулы (4.1.24), (7.1.16) в [4])

rr         q ⁽ x o , y o )

Q V⁽ x ^- x 0 ^{)2 + (} y - y 0 ⁾²

dx ₀ dy ₀ = 2 n9 [ 5- f ( x , y )], ( x , y ) e Q ,

A 11 A 33   A b

.

⁽ Y 1 +Y 2 ) A_n

Здесь δ ― осадка штампа под действием силы P ; f ( x , y ) ― функция, описывающая форму основания штампа; Ω ― область контакта; q ( x , y ) ― контактное давление в области Ω ; γ 1 , γ 2 ― корни характеристического уравнения (3) (с положительной вещественной частью). Уравнение (7) отличается от ИУ контактной задачи для изотропного полупространства только контактной жесткостью θ . Полагая в формуле (8) ( G ― модуль сдвига, ν ― коэффициент Пуассона)

A 11

л    2 G (1 -v )

= A ³³ =       v ’

A 13 =

2 G v

1 - 2 v ’

Y 1 = Y 2 = 1,

получим известное выражение контактной жесткости для изотропного случая:

9 = -G- .

1 — v

Для случая эллиптического параболоида

2        2

f ( x , y ) = -  + ^  , ^ , >  R ₂,

2 R 1    2 R ₂    ^{1    2}

точное решение ИУ (7) выражается через полные эллиптические интегралы

K ( e ) = Г       ^{d ф}     -, E ( e ) = [ ^ 1 - e ² sin ² _Ф d ф , D ( e ) = K ⁽ e ) - E ⁽ e )

^J V 1 - e ² sin ² ф            ^J                                  e 2

и имеет вид [4, c. 210–212], сравните с формулами (4)–(6),

q ⁽ x , y ) = q 0   ¹

-

x ² a ²

-

y! P = b ² ,

JJ q ⁽ y , z ) dydz = 2 П ^abq 0 ,

Ω

5 = bq ⁰ K ( e ), 2 9

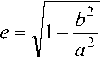
a ² K ( e ) _      R_i _ K ( e ) - E ( e )

2 R D ( e ) = ’ R ₂ = (1 - e ²) D ( e )"

При заданных величинах 5 , R 1 , R 2 величина e (12) и отношение полуосей эллипса контакта а / b определяются из второго соотношения (13). Затем величина a находится из первой формулы (13), величина q 0 ― из первой формулы (12). Вдавливающая сила рассчитывается по второй формуле (11).

Имея решения для двух случаев контактной задачи, изображенных на рис. 1, сравним в этих решениях значения сил, необходимых для вдавливания штампа на одну и ту же величину, а также отношения сил к площади контакта. Допустим, что области контакта находятся в квадратах со стороной h . В «традиционной» контактной задаче введем безразмерные величины (штрихи затем опускаем)

, x     , у   „,   5     ,      h            h          а x ' = —, у ' =    , 5 ' =   , A =      , B =       , a ^=   , h      h      h      2 R i       2 R 2       h

b ' = b ,                              (14) h

q'(x', У') =

q(x, у) 2лв ’

-q^, P' =

2 лв       2 лв h²

и рассмотрим ниже случай кругового штампа: 5= A = B = 1. Тогда на основании формул (11)-(15) безразмерное решение осесимметричной контактной задачи имеет вид

,    .   2^2  Г

q(x, у) = п2

l - 2 x ² - 2 у ², P =  q ( x , у ) dxdy = ЗА.

3п

п

В «нетрадиционной» контактной задаче введем безразмерные величины (штрихи затем опускаем)

у '= у , h

z 5    h    h   ab z ' = — , 5 ' =   , A =      , B ' =       , a ' =   , b ' =   ,                                (17) 7                  7                                                                        7                  7 h       h       2 R-i        2 R. 2        h       h q '( x ', у ') = q^x^^l , q 0' = -q 0-, P ' = - P y.                                    (18) A 66          A 66        A 66 h 2

Тогда на основании формул (1), (4)–(6), (17), (18) безразмерное решение имеет вид

yz

q ⁽ у , z ) = q о ^{1 -} ту ^- т, P = ba

JJ q ⁽ У , z ) ^dУ^dz = у abq о , п

⁽ m l ^- m 2 ) Y ^{2 2}Г      Z i ( y ) Z 2W cos² Ф d Ф

8       ^J D ( ф )[( а / b )²cos² ф + sin² ф ]^1/2,

Ab ² + Ba ² =5 ,   B = - .

A d

Также рассмотрим случай кругового штампа: 5= A = B = 1. Из формул (8), (15), (16), (18) и (19) заключаем, что отношение размерной силы P = P 1 («традиционный» случай) к размерной силе P = P 2 («нетрадиционный» случай) для кругового штампа находится по формуле

P i    272    An A 33 - A ²

---- = -----------•--------------------------.

^р 2    ^{п a} bq 0   ⁽ Y i +Y 2 ) A il A 66

Механика

где a , b и q 0 находятся по формулам (20)-(21) при 5= A = B = 1.

Важную роль играет отношение T = P / S силы P к площади контакта S . Из формул (16), (19) и (22) заключаем, что для кругового штампа отношение T = T 1 для «традиционного» случая связано с отношением T = T ₂ для «нетрадиционного» случая по формуле

T 1   4V2

T 2    ^{п q} 0

A ll A 33    A 13

•-----------------------------------------------------.

⁽ Y i +Y 2 ) A il A 66

при этом a , b и q 0 находятся по формулам (20)-(21) при 5= A = B = 1.

В табл. 1 для ряда материалов приведены результаты расчетов по формулам (20)-(23) при 5= A = B = 1.

В [7] введено понятие жесткости поверхности «нетрадиционного» трансверсально изотропного полупространства вдоль осей координат. Анализ данных табл. 1 показывает, что обычно P 1 > P 2 и T 1 > T ₂, если поверхность материала более жесткая в направлении оси y (исключения: Al 2 O 3 , SiC, бетон, состаренный циклами нагрев-холод). Кроме того, как правило, P i < P 2 и T 1 < T ₂, если поверхность материала более жесткая в направлении оси z. Изменение площади контакта при изменении направления вдавливания для материалов из табл. 1 незначительно и поэтому отличие отношения T 1 / T 2 от отношения вдавливающих сил невелико (см. две последние колонки табл. 1).

Значения характеристик (безразмерные)

Таблица 1

Материал	е= a / b	a	b	q 0	P 1 / P 2	T 1 / T 2
Al 2 O 3	1,00	0,708	0,706	2,46	1,06	1,06
Co	0,958	0,692	0,722	2,85	1,20	1,20
Mg	0,992	0,704	0,710	2,60	1,04	1,04
SiC	1,02	0,715	0,699	2,10	1,00	1,00
Ti	0,934	0,683	0,731	3,01	1,22	1,21
CdS	0,984	0,701	0,713	2,94	1,10	1,10
GaS	1,32	0,796	0,605	1,81	0,255	0,245
GaSe	1,21	0,771	0,637	1,99	0,381	0,374
ZnO	0,988	0,703	0,712	2,86	1,04	1,04
Углеволокно	0,764	0,607	0,795	3,88	5,60	5,41
Графит	2,09	0,902	0,432	1,71	0,0110	0,00856
Сапфир	1,01	0,710	0,704	2,36	0,992	0,992
Древесина	0,971	0,697	0,717	2,96	1,49	1,49
Керамика PZT-4	1,03	0,719	0,696	2,72	0,852	0,852
Композит (60% волокон)	0,852	0,649	0,761	3,23	4,48	4,42
Бедренная кость человека	0,962	0,693	0,721	3,39	1,20	1,20
Сырая бычья бедренная кость	0,950	0,689	0,725	2,99	1,49	1,49
Эпоксидное стекло	0,940	0,685	0,729	2,73	2,04	2,03
Эпоксидный графит	0,842	0,644	0,765	3,26	4,76	4,69
Гнейс влаго-пропитанный (минерал)	1,09	0,737	0,676	2,42	0,749	0,747
Бетон, состарен химически	0,972	0,697	0,717	2,17	1,17	1,17
Бетон, состарен циклами нагрев-холод	0,972	0,697	0,717	2,35	0,953	0,952

Заключение. Сравнение точных решений пространственных контактных задач для трансверсально изотропного полупространства важно для интерпретации результатов численных решений для конического, пирамидального и др. штампов. С практической точки зрения оба точных решения важны, например, при расчете контактной прочности выработок горных пород.