Сравнение турбулентных замыканий в одномерной модели водоема

Активное развитие технологий кластерных вычислений и рост мощностей суперкомпьютеров привели к тому, что разрешение моделей Земной системы будет составлять около 0.25°-0.5° ( 25-50 км). При таком разрешении многие ранее подсеточные объекты на земной поверхности, такие как водоемы, реки, болота и т.д., становятся крупномасштабными структурами и должны описываться явно.

Одной из составляющих деятельного слоя суши являются внутренние водоемы, играющие важную роль в формировании локальных погодных условий и во многом определяющие специфические особенности климата над прилегающей территорией. Прежде всего это обусловлено существенной разницей между температурой поверхности озера и температурой поверхности окружающей его суши. Эта разница наблюдается почти всегда, за исключением случаев, когда и озера, и почва покрыты снегом. Существенно отличие между водными объектами и сушей и в других термо- и аэродинамических характеристиках поверхности, таких как шероховатость и альбедо. Все это приводит к значительной пространственной неоднородности турбулентных и радиационных потоков на поверхности, особенно в регионах, где высока плотность количества озер, например, на Западно-Сибирской низменности. Контраст в потоках энергии на границе земля-вода имеет суточный цикл, приводящий к местной атмосферной циркуляции вдоль берегов крупных озер во время безледного периода. В умеренной климатической зоне наличие крупных водоемов изменяет теплообмен в приземном слое воздуха на сезонном временном масштабе. В течение лета водоемы, прогреваемые коротковолновой солнечной радиацией, накапливают тепло, а в течение осени выделяют это тепло, вследствие больших градиентов температуры и влажности между поверхностью водоема и воздухом. Тепло, выделяющееся с поверхности озер в конце осени и в начале зимы, часто приводит к развитию горизонтальных конвективных ячеек в пограничном слое атмосферы в условиях холодного атмосферного вторжения -классический сценарий, тщательно изученный в районе Великих американских озер (например, [1]). Эти примеры ясно показывают важность реалистичного представления озер в моделях численного прогноза погоды и в моделях Земной системы.

Современный этап развития схем деятельного слоя суши в моделях Земной системы характеризуется усложнением параметризаций гидрологических процессов. Описание многих процессов, связанных с движением и фазовыми переходами воды (перенос и фазовые переходы влаги в почве, процессы формирования и развития снежного покрова, движение и транспирация влаги в растениях), присутствует в этих моделях сравнительно давно. В параметризациях водоемов [2], [3], [4], [5] основной упор делается на термодинамику взаимодействия с атмосферой, а моделирование скорости течения (имеется не во всех параметризациях) служит для адекватного воспроизведения вертикального турбулентного теплообмена внутри водоема. Потоки явного скрытого тепла и импульса служат граничным условием для атмосферных моделей, поэтому от моделей водоемов требуется, в первую очередь, точность расчета этих величин. Однако адекватное воспроизведение вертикального профиля температуры в водоеме также имеет большое значение, поскольку температура является ключевым фактором развития экосистем, которые могут оказывать влияние на атмосферные процессы. Так, в последнее десятилетие заметное внимание уделяется эмиссии метана с внутренних водоемов, в частности, термокарстовых озер [6]. Усиление образования метана при участии соответствующих микроорганизмов может быть обусловлено повышением температуры грунта, вызванным потеплением климата.

Одномерные модели водоема в силу вычислительной простоты хорошо подходят для климатических задач, в которых рассматриваются большие территории, большое количество водоемов и приходится проводить длительные численные эксперименты [2].

В рамках развития климатического моделирования к модели водоема выдвигаются требования к вычислительной эффективности, физической адекватности всех её параметризаций и возможности использования грубых шагов по времени, т.е. порядка 1 часа. Также появляются требования к универсальности данной модели для разных климатических зон.

Требование вычислительной экономичности, приводящее к ограничению шагов по пространству и по времени в модели водоема, вынуждает исследовать чувствительность численного решения и его сходимость в модели при варьировании этих шагов на примере идеализированных течений, демонстрирующих роль отдельных ключевых механизмов теплообмена в водоеме, и на реальных объектах с дальнейшим сравнением с данными измерений.

2.    Методология

В настоящей работе используется одномерная модель озера LAKE 2.0 [7]. В ней трехмерные уравнения для скалярных величин и скорости усредняются по горизонтали для водоема произвольной формы, однако здесь эта форма для простоты будет задана параллелепипедом. В модели вертикальный профиль температуры находится как решение уравнения притока тепла, в отличие, например, от наиболее распространенной двухслойной модели FLake [4]. При этом, в отличие от модели Хостетлера [3] и основанного на модели Хостетлера программного кода CLM-LISSS4 [8], в модели LAKE реализован биогеохимический блок [7,9], который воспроизводит продукцию и эмиссию газов СН4 и СО2 в атмосферу.

В отличие от модели Хостетлера и CLM-LISSS4, турбулентные коэффициенты теплопроводности и вязкости в модели LAKE находятся по формуле Колмогорова [14]:

fc2 ^2

^ = Се ~, ^Т = Се,Т где Се и Се,т - эмпирические констатны (см. табл. 4 в Приложении 1), турбулентная кинетическая энергии (ТКЭ) к и скорость ее диссипации е находятся на основе турбулентного замыкания к — е (см. Приложение 1). Данное турбулентное замыкание широко распространено при решении задач технической и геофизической гидродинамики. В моделях геофизической гидродинамики, в частности, были показаны границы ее применимости и численной устойчивости при включении в дискретную трехмерную систему семи уравнений Рейнольдса ([10], см. также работу [И]).

В настоящей работе в модель LAKE 2.0 была добавлена параметризация теплопроводности Хендерсон-Селлерс [12] (см. Приложение 2) для устойчиво стратифицированных озер совместно со схемой конвективного перемешивания водоема при неустойчивой стратификации [13].

В стандартной к — е модели коэффициент в формуле Колмогорова считается константой. Однако при стратификации, отличной от безразличной, более физически обоснованно считать данный коэффициент функцией стратификации и сдвига скорости; такие функции предложены, например, в работах Капуто и соавт. [15], Гальперина и соавт. [7] (см. табл. 4 в Приложении 1).

Для анализа точности численного решения и скорости его сходимости при различных вариантах замыкания к — е и в параметризации Хендерсон-Селлерс, а также для оценки правильности воспроизведения в модели основных физических механизмов перемешивания авторами работы был проведен ряд численных экспериментов как для идеализированных течений, так и для реальных озер.

Необходимым условием сходимости конечно-разностного решения системы дифференциальных уравнений к точному является стремление к нулю нормы разницы конечноразностных решений с различным пространственно-временным разрешением при стремлении шагов по времени и пространству к нулю.

Конечно-разностная схема модели LAKE 2.0 - схема Кранка-Николсон с центральными разностями по пространству. Она консервативна по всем первым моментам и по энергии среднего течения. Перенос энергии между средним течением и ТКЭ в схеме реализуется аналогично переносу в исходной дифференциальной постановке.

3.    Эксперимент Като—Филлипса для к — е модели

Рассматривается идеализированный сценарий ветрового перемешивания водоема, следующий в своей постановке классическому лабораторному эксперименту [17]. В этом эксперименте перемешанный слой, индуцируемый постоянным касательным напряжением на поверхности, проникает в линейно стратифицированную жидкость. Лабораторные данные роста глубины перемешанного слоя D_m со временем t хорошо аппроксимирует следующая формула [18]:

Dm(t) = 1.05n^ No^1/2t^1/2,                                  (1)

где n* - скорость трения на поверхности, а постоянная No - частота Брента-Вяйсяля начального профиля температуры Т (плотности).

В рамках данного идеализированного эксперимента проведены исследования чувствительности численного решения к пространственному и временному разрешению и сходимости при различных вариантах расчета коэффициента Колмогорова в к — Е замыкании (табл. 2) и возможности воспроизведения заглубления перемешанного слоя как одного из важнейших параметров правильного воспроизведения состояния водоемов.

Эксперимент проводился с использованием модели LAKE, настроенной для данного эксперимента. На нижней и верхней границе был задан нулевой поток тепла. Начальный профиль температуры задавался как линейный:

Т (z) = az + 3

с параметрами a = —3 К/м, 3 = 333 К, где ось z направлена вдоль вектора силы тяжести. Начальная скорость течения полагалась равной нулю и глубина водоема задана 20 м. Параметр Кориолиса принимался равным 0. Следуя работам [19,20], используем следующие значения параметров:

и*_д = 3 • 10^-3 мс^-1     и     No = 5.5 • 10^-2 с^-1.

Для каждого из подвидов турбулентного замыкания к — е проводились две группы численных экспериментов (табл. 1) с варьированием шага по времени АД и с фиксированным количеством уровней по вертикали М , а также с варьируемым количеством уровней по вертикали М^к, но с фиксированным шагом по времени At.

Таблица!

Пространственное и временное разрешение в двух группах численных экспериментов

Аббревиатура группы	Фиксируемый параметр пространственновременного разрешения	Варьируемый параметр пространственно-временного разрешения	Диапазон индексов эксперимента
Гр.1. к	At = 25 с	Мк = 10; 20; 40; 80; 160; 320;640	к = 1..7
Гр.2. к	М = 40	АД = 3600; 1800; 900; 450;225;100;50; 25 с	к = 1..8

Согласно сформулированному необходимому условию сходимости численного решения в каждой группе экспериментов сходимость оценивалась по стремлению к нулю среднеквадратического отклонения cr^k'^k+1 поля температуры Т^к относительно поля Т^к+1 (к -номер эксперимента):

^к,к+1

N М

—1— У У (Тк м • N ^   ( i,j i=i j=i

-

Т ^к+1)2

Тм ) ’

здесь М - количество уровней сетки, N - количество шагов по времени.

3.1.    Результаты эксперимента

Для того чтобы проверить сходимость решения на больших временах в модели необходимо задать такую глубину водоема, чтобы перемешанный слой длительное время развивался, не достигая дна. Поэтому при заданном градиенте температуры ее значение на поверхности становится неправдоподобно высоким для реальных водоемов (60 °C), хотя такую же стратификацию по плотности (частоту Брента-Вяйсяля) можно задать и распределением по вертикали солености.

Среднеквадратическое отклонение между результатами экспериментов Гр.1.3 и Гр.1.4 составляет около 0.26 °C, как видно из рис. 1, что в практическом смысле можно считать удовлетворительной мерой сходимости, т.к. оно близко к погрешности измерений температуры гидрометеорологическими приборами. При этом в эксперименте Гр.1.1 (At = 25 с, Н ¹ = 10) для всех вариантов замыкания к — е имеет место существенная ошибка в глубине перемешанного слоя относительно аналитического решения [18] (рис. 4).

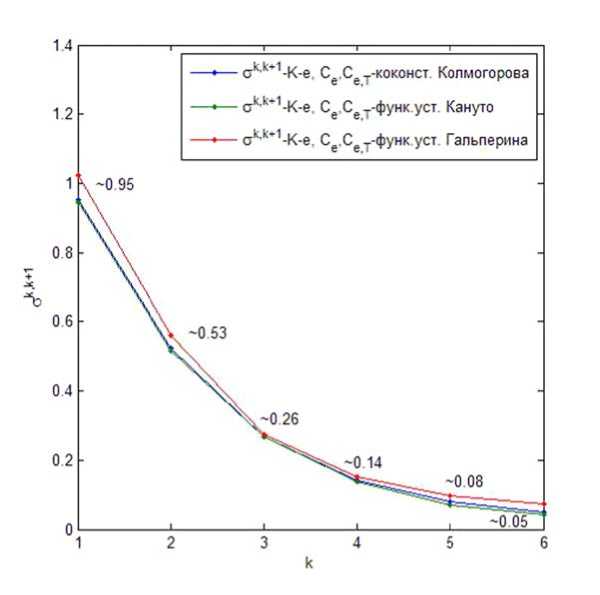
Рис. 1. Средпеквадратическое отклонение для группы экспериментов Гр.І.к, где узел 1 по оси абсцисс соответствует средпеквадратическому отклонению между экспериментами Гр.1.1 и Гр.1.2 и так далее

Как видно из рис. 2 (характерного для всех трех вариантов замыкания к — е), при достаточно высоком вертикальном разрешении глубина перемешанного слоя и распределение температуры близки к аналитическому решению для эволюции глубины перемешанного слоя (1). Только в случае функций устойчивости Гальперина глубина перемешанного слоя меньше аналитической оценки на ~1 м (5%).

Эксперименты Гр.1 показывают, что модель водоема с замыканием к — е, начиная с эксперимента Гр.1.4 ( М = 40, при шаге сетки ^ 6 0.5 м), рассчитывает глубину перемешанного слоя, близкую к аналитическому решению.

В экспериментах Гр.2.1 (At = 3600 с). Гр.2.2 (At = 1800 с) Гр.2.4 (At = 450 с) поведение изотерм характеризует потерю точности решения при таких шагах по времени для неявной схемы решения системы уравнений модели (рис. 3).

к

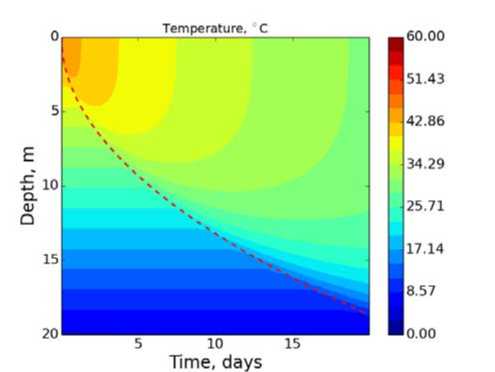
Рис. 2. Поле температуры в эксперименте Гр 1.7, Ді = 25, Н ⁷

= 640, характерное для замыкания

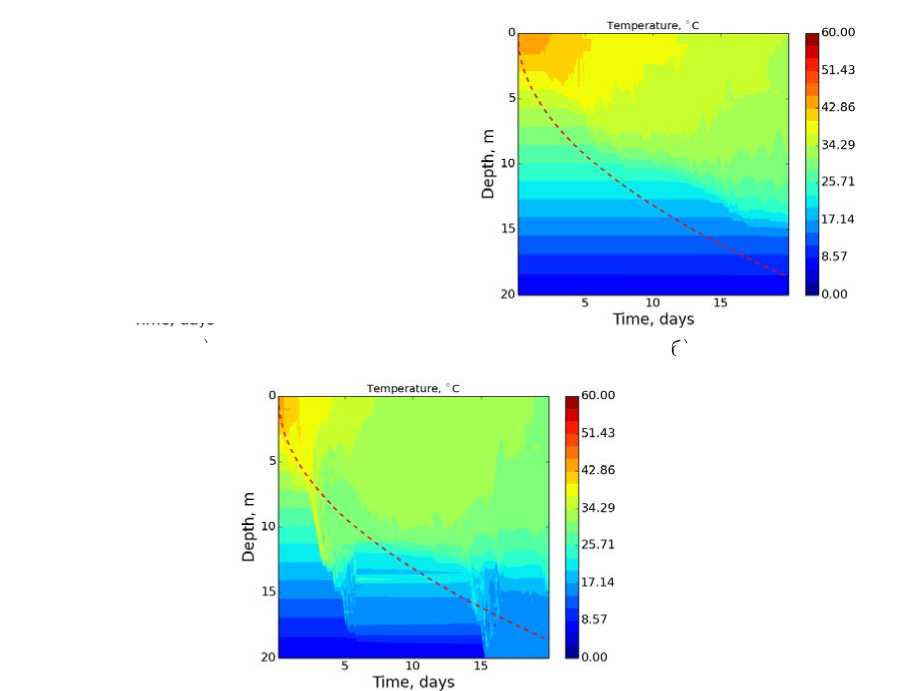
а)

б)

в)

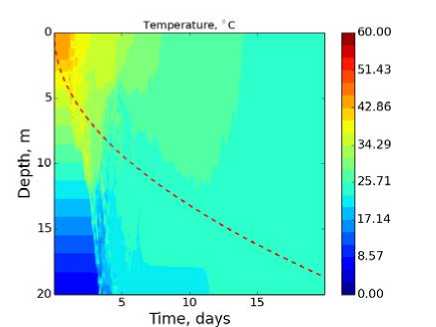
Рис. 3. Поле температуры в экспериментах Като-Филлипса, группы Гр.2.1 с моделью LAKE при использовании к — е замыкания: а) с С; и С;,т как эмпирическим и константами; б) с С; и С;,т как функциями устойчивости Капуто; в) с С; и С;,т как функциями устойчивости Гальперина

е

Для экспериментов Гр.2.5, Гр.2.6, Гр.2.7 Гр.2.8 получается достаточно точное решение для температуры, близкое к решению, изображенному на. рис. 2. При этом из рис. 4. видно, что решение с приемлемой точностью достигается при шаге по времени Ді = 100 с.

Таким образом, эксперименты Гр.2 показали, что в случае устойчивой стратификации при постоянном напряжении ветра модель с замыканием к — е (со всеми вариантами ко- эффициентов Колмогорова) может даватв гладкое решение толвко с шагом по времени At < 450 с, а сходимость достигается при At < 100 с.

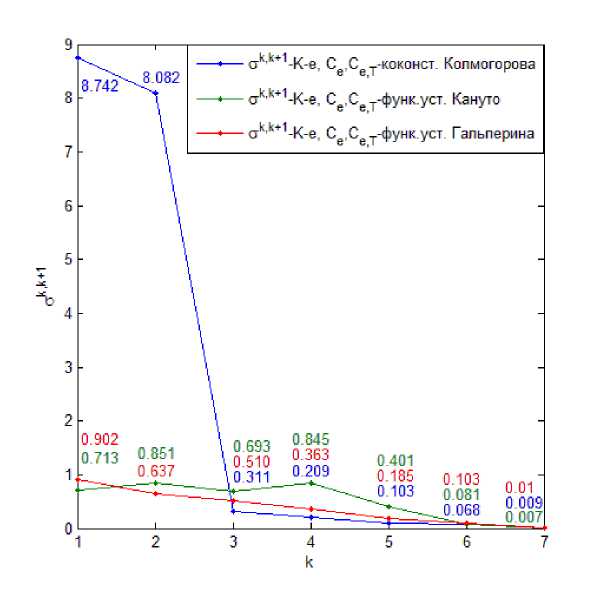
Рис. 4. Средпеквадратическое отклонение для группы экспериментов Гр.2.к, где узел 1 по оси абсцисс соответствует средпеквадратическому отклонению между экспериментами Гр.2.1 и Гр.2.2 и так далее

4.    Эксперимент с реальным атмосферным форсингом для модели LAKE с параметризацией Хендерсон-Селлерс и к — е моделью

Эксперимент для озера Куйваярви (Финляндия; глубина - 12.5 м) проведен с атмосферным форсингом из данных измерений, выполненных университетом Хельсинки с 1.05.2013 по 10.11.2013 [21]. Для модели LAKE с параметризацией Хендерсон-Селлерс проводились две группы численных экспериментов (табл. 2): в первой группе варьировался шаг по времени At и фиксировалось количество уровней по вертикали М' во второй группе изменялось количество уровней по вертикали М^к, а шаг по времени At принимался постоянным.

Т а б л и ц а 2

Шкала пространственного и временного разрешения двух групп численных экспериментов

Аббревиатура группы	Фиксируемый параметр пространственновременного разрешения	Варьируемый параметр пространственно-временного разрешения	Диапазон индексов эксперимента
Гр.1. к	At = 25 с	Мк = 12;24; 48; 96;192	к = 1..5
Гр.2. к	М = 40	At = 3600; 1800; 900; 450;225;100; 50 с	к = 1..7

4.1.    Результаты эксперимента

Результаты эксперимента для Гр.2 с моделью LAKE, включающей параметризацию Хендерсон-Селлерс, показали очень слабую чувствительность конечно-разностной схемы модели LAKE к варьированию шага по времени (рис. 5а). Варьирование шага по пространству в экспериментах Гр.1 показало, что модель в такой конфигурации чувствительна к шагу по времени характерном для эксперимента Ppl.1 ( М = 12). При уменьшении пространственного шага модель вела себя, как и в случае экспериментов для Гр.2 (рис. 56).

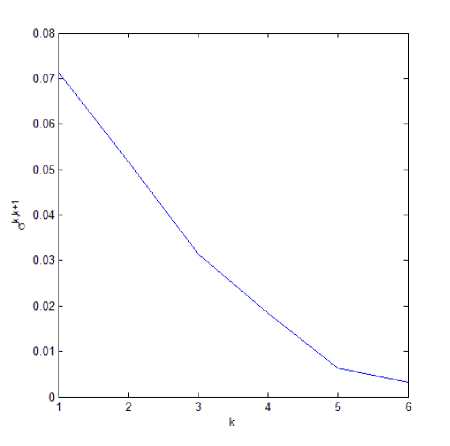
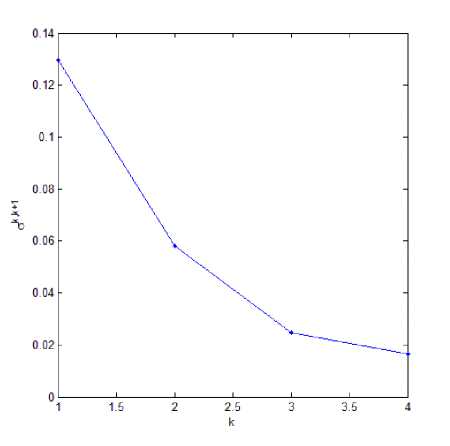
а) б)

Рис. 5. Средпеквадратическое отклонение полей температуры в экспериментах с реальным атмосферным форсингом для группы экспериментов: а) Гр.2.к, где абсциссе 1 соответствует средпеквадратическое отклонение между экспериментами Гр.2.1 и Гр.2.2 и так далее; б) Гр.1.к, где абсциссе 1 соответствует средпеквадратическое отклонение между экспериментами Гр.1.1 и Гр.1.2 и так далее

Эксперименты группы Гр.2. (различные варианты задания Сі,Сқт) для модели LAKE с к — е замыканием показали, что неустойчивость численного решения имеет место при At > 450 с. Для экспериментов Гр.2.4 и Гр.2.5 характерно распределение температуры, показанное на рис. 6.

В экспериментах Гр.2.6 и Гр.2.7 удалось воспроизвести близкое к измеренному поле температуры (рис. 7).

В ходе численных экспериментов измерялось также время счета модели на персональном компьютере t (табл. 3).

Для сравнения с измеренным пространственно-временным распределением температуры использовались данные экспериментов с параметрами At = 25 с, М = 48 для модели с LAKE с к — е замыканием (с различными вариантами С/, Сқт) и At = 3600 с, М = 48 с параметризацией Хендерсон-Селлерс.

Результаты приведенных экспериментов с моделью LAKE с замыканием к — е (при разном задании коэффициентов Колмогорова) с реальным атмосферным форсингом приводят к таким же выводам об условиях сходимости численного решения, что и в экспериментах Като-Филлипса. Приемлемая точность решения достигается при At 6 50 с. Эксперименты с моделью LAKE при использовании параметризации Хендерсон-Селлерс показали, что приемлемая точность решения достигается при значительно более грубых шагах как по пространству, так и по времени.

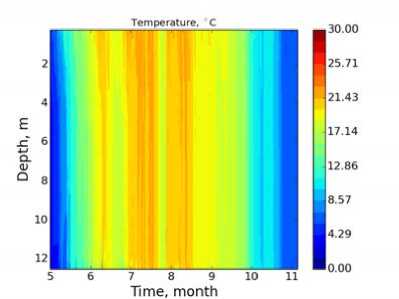
а)                                                      б)

в)

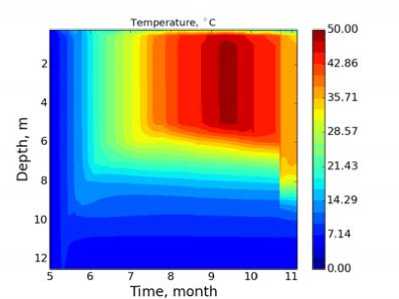
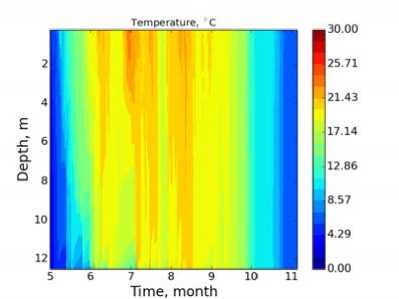
Рис. 6. Поле температуры в экспериментах Гр.2.4 (At = 450 с) и Гр.2.5 (At = 225 с) с реальным атмосферным форсингом для оз. Куйваярви: Коэффициенты формулы Колмогорова Сі и C ( l, Т заданы как: а) эмпирические константы Колмогорова; б) функции устойчивости Капуто; в) функции устойчивости Гальперина

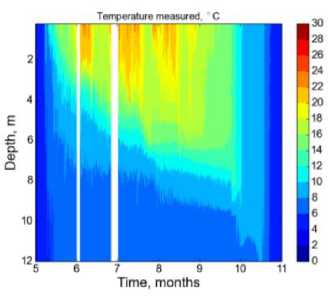
Сравнение с данными измерений (рис. 76) показывает, что модель с параметризацией Хендерсон-Селлерс (рис. 7а) качественно воспроизводит распределение температуры с глубиной, а также динамику перемешанного слоя, незначительно занижая его глубину в среднем на 1 м, кроме октября и ноября, для которых она значительно занижает глубину на 2.5-3 метра. Кроме того, в августе модель не воспроизводит скачок в заглублении перемешанного слоя, связанный, по-видимому, с сильным ветровым напряжением и выхолаживанием поверхности. Тем не менее эти отклонения не сказываются существенно на качестве воспроизведения температуры поверхности водоема.

Т а б л и ц а 3

Время, затраченное вычислительной машиной для расчета экспериментов с реальным атмосферным форсингом для оз. Куйваярви

Параметризация турбулентного обмена	At с	М = 24	М = 48	М = 96
Хендерсон-Селлерс	3600 с	11 с	16 с	18 с
к — е	3600 с
Хендерсон-Селлерс	25 с	192 с	247 с	349 с
к — е	25 с	225 с	313 с	471 с

а)

б)

Time, month

в)

Time, month

г)

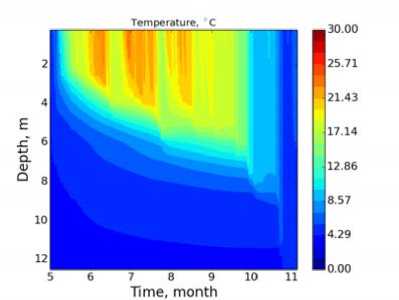
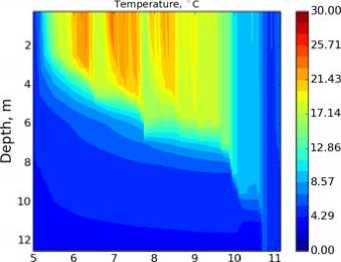
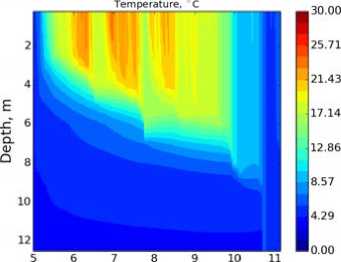
д)

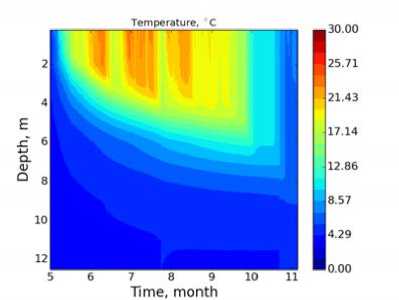
Рис. 7. Распределение температуры по глубине и времени для озера Куйваярви: а) модель LAKE с параметризацией Хендерсон-Селлерс; б) данные измерений; в) LAKE с замыканием к — е эмпирическими константами Колмогорова г) LAKE с замыканием к — е с функциями устойчивости Капуто; д) LAKE с замыканием к — е с функциями устойчивости Гальперина

Модель с замыканием к — е с различными вариантами коэффициентов Колмогорова (рис. 7в, 7г, 7д) достаточно качественно воспроизводит измеренное распределение поля температуры, динамику заглубления перемешанного слоя и скачок температуры в августе. Более точно, нежели для параметризации Хендерсон-Селлерс, воспроизводится глубина перемешанного слоя в осенний период. Стоит также отметить, что модель с замыканием к — е с функциями устойчивости Гальперина, так же как и для эксперимента Като-Филлипса, занижает глубину перемешанного слоя и сглаживает скачок, характерный для августа.

Эти результаты, а также анализ табл. 3 показывают, что в качестве параметризации для расчета коэффициента турбулентной теплопроводности можно использовать параметризацию Хендерсон-Селлерс и при больших шагах по времени Ai = 3600 с, с сокращением времени счета в 20 раз по сравнению с расчетом для At = 25 с. Разные версии замыкания к — Е воспроизводят фактически одинаковую динамику поля температуры и заглубление перемешанного слоя и в рамках экспериментов эмпирические константы Колмогорова дают такой же или лучший резулвтат, чем математически сложные функции устойчивости Гальперина и Кануто.

5.    Заключение

Эксперимент Като-Филипс, а также эксперименты для озера Куйвоярви показали, что модель с замыканием к — е (со всеми вариантами коэффициентов Колмогорова) может давать гладкое решение только с шагом по времени At < 450 с, а сходимость достигается при At < 100 с. При этом результаты сравнения с данными измерений показывают, что модель с параметризацией Хендерсон-Селлерс, так же как с замыканием к — Е, качественно воспроизводит распределение температуры с глубиной, а также динамику перемешанного слоя. При этом сходимость численного решения при использовании замыкания Хендерсон-Селлерс достигается при значительно более грубом временном разрешении, чем для замыкания к — е. Эти результаты показывают, что при больших шагах по времени, At = 3600, в одномерной модели водоема в качестве параметризации коэффициента турбулентной теплопроводности можно использовать параметризацию Хендерсон-Селлерс, что делает модель водоёма лучше приспособленной для применения в рамках моделей Земной системы, а также моделей прогноза погоды накладывающих ограничение на шаг по времени в параметризациях деятельного слоя суши.

6.    Приложение 1

Прогностические уравнения для ТКЭ, к и скорости ее диссипации е имеют вид

= OLd +      + s + в—* =      ++ . (cis+«в - С2Е), dt dz \     Ок у dz             dt dz \     ae ) dz к s = - [(^ У + ( F УЬ = —    («г дТ + «. °? ),

\ dz)    \ dz)          pwo   d dz dz)

к2             к2

- = Ce ""^Т = Се,г — , здесь «г(Т, s) обозначает коэффициент термического расширения, as(T, s) - коэффициент расширения относительно солености s. Постоянные коэффициенты и функции устойчивости приведены в табл. 4.

Граничные условия для ТКЭ и е задаются одинаково для нижней и верхней границ и записаны выражениями, точными в приближении логарифмического пограничного слоя [21]:

-Эк            - Эе           ₃/₄ - к^3/2

°к dz z=0,h     , °е dz z=0,h       e,0 О Kzl ’ где Ce,o = 0.09 - постоянный коэффициент Колмогорова для импульса, zo = 10-2 м -эмпирический параметр, к = 0.38 - константа Кармана.

Уравнения для горизонтальных компонент импульса имеют вид [7]:

$=°z (<^-+^ й)^{+ +;}”-⁰⁵ =°z (<^-+^ Ю^{+ —f}"-

7.    Приложение 2

Уравнения для параметризации коэффициента турбулентной температуропроводности для термически стратифицированного водоема имеют вид [7]:

Т а б л и ц а 4

Коэффициенты стандартной к — е модели

Константы

O k	1
oe	1.111
Oe1	1.44
Oe2	1.92
Oe3	1.14
Константы Колмогорова. [22]
Ce	0.09
C e,T	0.072
Константы Колмогорова, как функции устойчивости Кануто [15] и как функции устойчивости Гальперина. [7]
С е	Функция устойчивости (стратификации и сдвига, скорости) для импульса
C e,T	Функция устойчивости (стратификации и сдвига, скорости) для скаляров

KU qZ     * ~ /           о \ — 1

VT =      е-кг (1 + 37Дг2) 1, ро где

_ —1 + [1 + 40N .2 z ² / (и**²е^-к* ^z )] ²

где Ро - нейтральное значение туріэулентного числа. Прандтля, z. м - глубина. N, с^-1 - ча стота Брента-Вяйсяля, к - константа Кармана, к* считается функцией широты и скорости как обобщение аналитического решения Смита. [23] для всех широт:

к* = 6.6^sin(^)U-L84, где у - широта, U мс-1 - горизонтальная скорость ветра на высоте 10 м, и* мс-1 - скорость трения на. поверхности, которая рассчитывается из предположения, что длина, смешения постоянна, в экмановским слое, по формуле

и* = 1и * (—к* ),

• l(z), м - глубина перемешанного слоя, и * , мс^-1 - скорость на поверхности.

Расчет идеализированных экспериментов, оценка, сходимости и устойчивости выполнены при поддержке гранта. РНФ 17-17-01210 «Исследование процессов взаимодействия атмосферного пограничного слоя умеренных и высоких широт с деятельным слоем суши и водоёмами: разработка, параметризаций для моделей Земной системы». Получение данных измерений, сравнение с численными экспериментами выполнены при поддержке проекта. IX.138.2.1 программы фундаментальных исследований СО РАН.