Сравнение устойчивости вихревых пучков Лагерра-Гаусса к случайным флуктуациям оптической среды

Влияние атмосферы и других случайных сред на распространяемые через них лазерные пучки является объектом научных и инженерных исследований на протяжении более ста лет. Актуальность этих исследований возросла в связи широким применением лазеров в оптических системах, работающих в атмосфере, океане, биологических тканях и т.п.

Одним из основных приложений световых пучков является беспроводная оптика ( Free-Space Optics , FSO), когда оптический канал проходит через случайную среду или вакуум. Практически неограниченный трафик сигнала на оптических частотах является выигрышной особенностью, которая отличает оптический канал от классической линии связи (радиоволны). С появлением высоконаправленного лазерного излучения дополнительное преимущество оптической коммуникации, связанное с безопасностью, стало очевидным [1 –3]. Оптические сигналы также могут быть использованы в лазерных радарах (LIDARs) для дистанционного зондирования материальных объектов или в метеорологии [4].

Тем не менее, эффекты естественных случайных сред [5–9], такие как мерцание ( scintillation ), блуждание лучей ( beam wander ) и рассеивание от частиц, оказываемые на детерминированные (лазерные) световые пучки, оказались настолько серьезными, что это существенно повлияло на технические характеристики оптических коммуникационных систем и ограничило область их применения. Поэтому множество усилий направлено на поиск возможностей преодоления негативного влияния естественных случайных сред.

На сегодняшний день предлагаются несколько способов модификации оптического канала: использование частично когерентных пучков [1, 10– 12], лазерных пучков со специальной пространственной структурой (вихревые, бездифракционные, моды высших порядков) [13–16], векторных пучков с неоднородной поляризацией [17, 18], а также одновременно нескольких пучков с одинаковой или разными частотами [19, 20].

Заметим, что особый интерес для уплотнения каналов передачи информации представляют пучки, несущие орбитальный угловой момент и имеющие бесконечное число возможных квантовых состояний [21]. Уже продемонстрированы значительные успехи в применении такого способа уплотнения каналов как в волоконных системах связи [22], так и в свободном пространстве [23, 24]. Обзор по исследованию и применению вихревых пучков в случайных средах можно найти в работах [25,26].

Устойчивость вихревых пучков к случайному воздействию отмечалась в нескольких экспериментальных работах [13, 27–29]. Заметим, однако, что оптические вихри высоких порядков менее устойчивы к возмущениям оптической среды. В работе [13] было показано, что вихревые пучки высокого порядка сохраняются в турбулентной среде на значительном расстоянии (несколько километров), но затем расщепляются на вихри первого порядка. В этой же работе утверждалось, что вихревой пучок может расщепляться, отклоняться, блуждать вне области детектора, но никогда не исчезает, т.е. сохраняется общий угловой момент поля. В работе [29] было показано, что пучки с более высоким оптическим вихрем больше подвержены влиянию случайных флуктуаций, хотя при дальнейшем распространении (после искажения) в свободном пространстве демонстрируют лучшую способность восстановления. Этот эффект объяснялся фазовой структурой пучка.

В данной работе выполнено сравнительное численное и экспериментальное исследование пучков Лагерра–Гаусса, имеющих одинаковый вихревой топологический заряд, но различную пространственную структуру, а именно количество колец. В каждом кольце вихревая фазовая структура пучка повторяется, т.е. имеет место структурная избыточность. Это должно повысить устойчивость пучка к случайным возмущениям по аналогии с массивами пучков.

Так как важным свойством вихревых пучков является сохранение топологического заряда, то в численных и экспериментальных исследованиях данный па- раметр был выбран критерием устойчивости пучков. На первый план здесь выходит задача одновременного экспериментального детектирования нескольких вихрей с разными топологическими зарядами, присутствующих в пучке. В работе предлагается использовать для этой цели простой и надежный подход, основанный на согласованной корреляционной фильтрации. Реализация этого подхода выполнялась с использованием многоканального фазового ДОЭ, раскладывающего поле по угловым гармоникам [30,31].

1.    Численное моделирование

Распространение лазерного пучка через случайную среду можно моделировать с помощью интегрального выражения, соответствующего расширенному принципу Гюйгенса-Френеля [32,33]:

E ( u , v , z , t ) = - ( ik/2 n z ) exp( ikz ) x

MM x J J Eo(x,y)exp{(ik/2z)[(x-u)2 + (y- v)2]}x (1) -M -M x exp {^ (x, y, u, v, z) - i tot} dx dy, где Eo(x, y) - поле во входной плоскости (при z = 0), E(u, v, z, t) - поле на расстоянии z от входной плоскости, Т(x,y, u, v, z) - случайная часть в операторе распространения, связанная с турбулентностью атмосферы, to - частота колебаний лазерного излучения, t - время.

Выражение (1) соответствует методу Рытова [33], а функция Т ( x , y , u , v , z ) описывает случайные отклонения фазовой функции сферической волны, распространяющейся от исходной плоскости к выходной.

Рассмотрим алгоритм расчета распространения пучка в случайной среде с заданной корреляционной функцией. Для простоты изложения алгоритм приведен в двумерном случае, однако он легко обобщается на большую размерность.

Пусть известна корреляционная функция случайного поля в виде [33]:

R { exp [у ( x i , u _p0 ) ] , exp [у ( x 2 , u 2 , z ) ] ] =

Г 2                23                              (2)

= exp [-(1/Po (z)) ( xi - X2 ) J = ReXp[v] ( xi - x2, z ) , где p0(z) = (0,545C2k2z) - длина когерентности распространения сферической волны через турбулентную атмосферу, Cn2 - структурная постоянная среды. Отметим, что данная корреляционная функция зависит от разности между координатами x1 и x2, а не от каждой из них по отдельности. Более того, она не зависит от координат в выходной плоскости u1 и u2, а зависит лишь от расстояния z до неё.

Будем считать, что средняя интенсивность Гауссова пучка, проходящего через случайную среду, сохраняется, а для этого зададим среднюю амплитуду случайного поля равной единице:

(exp [у ( x , u , z ) ]^ = 1.                                (3)

Для генерации случайного поля U ( x ) воспользуемся методом, описанным в работе [29]:

U ( x ) = h ( x ) *^ ( x ),                                 (4)

где звёздочкой (*) обозначена операция свёртки, h ( x ) - детерминированная функция (импульсная характеристика), £ ( x ) - комплекснозначный белый шум с единичной дисперсией и корреляционной функцией, равной дельта-функции Дирака. Тогда:

U ( x ) = F ^{- 1} [ F [ h ( u ) ] F [ ^ ( u ) ] ] =

= F-1 [ F [ Ru (u)]F [^( u)]], где F [•] - оператор преобразования Фурье, Ru(x) -автокорреляция функции h(x).

Окончательно получаем случайное поле оптической среды:

U ( x , u , z ) = exp [y ( x , u , z ) J - /exp [y ( x , u , z ) ]^. (6)

Входной пучок будем рассматривать в виде мод Лагерра-Г аусса:

GLnm (r, Ф) = exp (-(r2/2о2)) (r/о)1 m x (7) xLm (r2 /о2) exp (imф), где индексы (n, m) определяют число колец и заряд оптического вихря соответственно, о - радиус перетяжки Гауссова пучка, Lm (•) - обобщенные полиномы Лагерра [35].

В табл. 1 показаны результаты моделирования распространения пучков Лагерра-Гаусса с длиной волны 0,532 мкм и радиусом луча 1 мм в случайной среде на расстояние l для различных сочетаний (n, m). Для каждого сочетания (n, m) приводятся распределения амплитуды и фазы в разных строках таблицы. Видны сильные искажения вихревой фазы, существенно зависящие от l, при том, что искажения амплитуды не так существенны и примерно одинаковы для различных l. Хотя в табл. 1 не приводятся данные для сочетаний (n, m), где менялся бы только один параметр, общий характер зависимости от l в различных строках таблицы примерно одинаков и позволяет сделать необходимые выводы. Прежде всего, очевидно, что уже просто попадание пучка в случайную среду без всякого распространения (l=0) уже приводит к искажениям, очень похожим на те, которые происходят и при дальнейшем распространении. Это служит обоснованием для применения при экспериментальном исследовании имитации случайной среды средой с сосредоточенными параметрами (ПЭТ-пленкой). Более того, при l = 0 фазовое распределение выглядит более случайным, чем получается при распространении, хотя амплитудные распределения выглядят одинаково случайными во всех плоскостях. Параметры моделируемого пучка таковы, что 300 мм являются для него ближней зоной (конфокальное расстояние для таких параметров около 6 м). Распространение Гауссова пучка в ближней зоне не должно приводить к существенному изменению радиуса кривизны, но при моделировании мы видим некоторое уменьшение радиуса кривизны для всех пучков на расстоянии 100 мм, которого при отсутствии случай- ной среды быть не должно. В целом же вихревая фаза неплохо сохраняется для всех пучков, что более подробно проанализировано дальнейшим моделированием. В табл. 2–4 приведены усредненные результаты мо-

Табл. 1. Моделирование распространения пучков Лагерра–Гаусса в случайной среде на расстояние l [мм]

делирования разложения пучков с разными ( n, m ), прошедших через случайную среду, по вихрям с порядками p = 1,10.

n = 0,

m = 3

n = 1,

m = 4

Исходное поле

l = 0

l = 100

l = 200

l = 300

n = 2, m = 5

Табл. 2. Коэффициенты разложения искаженного пучка с m = 1 по вихрям разных порядков в зависимости от n

m = 1 n = 0 n = 1 n = 2 n = 3 n = 4 n = 5 p = 0 0,00922 0,02341 0,00979 0,05748 0,03475 0,04716 p = 1 0,9456 0,90811 0,92048 0,86856 0,91958 0,90443 p = 2 0,03915 0,04492 0,04599 0,04092 0,03229 0,03478 p = 3 0,00403 0,01558 0,01353 0,01908 0,00709 0,00929 p = 4 0,00155 0,00677 0,00540 0,00645 0,00234 0,00146 p = 5 0,00032 0,00075 0,00291 0,00389 0,00162 0,00115 p = 6 0,00007 0,00041 0,00132 0,00119 0,00104 0,00061 p = 7 0 0,00006 0,00044 0,00178 0,00076 0,00038 p = 8 0 0,00003 0,00007 0,00050 0,00026 0,00046 p = 9 0 0 0,00003 0,00006 0,00011 0,00013 p = 10 0 0 0 0,00005 0,00008 0,00009 В каждой строке таблиц приведены усредненные результаты вычисления вклада вихря порядка р в зависимости от числа колец n в исходном пучке. В таблицах серым цветом выделены строки, соответствующие вычислению вклада вихря, который присутствовал в исходном пучке. Прежде всего, следует отметить, что общее снижение интенсивности полезного сигнала из-за случайных помех нигде не превышает 22 %, а по большей части составляет 5 – 10 %. Если выбором n оптимизировать это значение, то можно добиться сниже- ния до уровня не более 7 %. Что касается распределе-   личных от передаваемого) порядков, то нигде они не ния этих перекрестных помех по вихрям других (от-   превышают 4 %, если брать оптимальное n.

Табл. 3. Коэффициенты разложения искаженного пучка с m = 2 по вихрям разных порядков в зависимости от n

m =2	n =0	n =1	n =2	n =3	n =4	n =5
p =0	0,00043	0,00209	0,00176	0,00895	0,00415	0,00860
p =1	0,02510	0,02860	0,02171	0,03890	0,03193	0,03095
p =2	0,92355	0,90626	0,90938	0,86155	0,91954	0,90945
p =3	0,03500	0,03426	0,03873	0,05482	0,02921	0,03909
p =4	0,01199	0,01954	0,01364	0,01031	0,00513	0,00548
p =5	0,00322	0,00610	0,00711	0,01596	0,00472	0,00246
p =6	0,00056	0,00267	0,00517	0,00414	0,00234	0,00133
p =7	0,00011	0,00032	0,00202	0,00297	0,00122	0,00072
p =8	0	0,00014	0,00025	0,00140	0,00076	0,00078
p =9	0	0,00001	0,00015	0,00062	0,00060	0,00057
p =10	0	0	0,00003	0,00024	0,00033	0,00030

Табл. 4. Коэффициенты разложения искаженного пучка с m = 5 по вихрям разных порядков в зависимости от n

m =5	n =0	n =1	n =2	n =3	n =4	n =5
p =0	0	0	0	0	0,00001	0,00001
p =1	0,00014	0,00001	0,00004	0,00008	0,00020	0,00008
p =2	0,00169	0,00077	0,00029	0,00152	0,00225	0,00144
p =3	0,00750	0,00556	0,00622	0,00654	0,01974	0,01084
p =4	0,04570	0,02451	0,02737	0,02378	0,05522	0,04201
p =5	0,88500	0,92239	0,91367	0,87160	0,77713	0,90894
p =6	0,02961	0,02572	0,02233	0,03966	0,07045	0,01819
p =7	0,02470	0,00893	0,01246	0,02596	0,03486	0,00711
p =8	0,00262	0,00917	0,01037	0,01125	0,02407	0,00453
p =9	0,00230	0,00165	0,00447	0,01304	0,00762	0,00297
p =10	0,00052	0,00083	0,00167	0,00362	0,00334	0,00114

Теперь про зависимость от n : для вихрей низких (первого и второго) порядков наилучшие результаты дает пучок с n =0, для вихря с m =5 наилучший результат достигается при n = 1. По всей видимости, вышеупомянутая структурная избыточность начинает действовать только когда вихрь более высокого порядка больше подвержен влиянию случайных флуктуаций и требует усреднения по большей площади.

2.    Экспериментальные результаты

Имитация случайной среды в эксперименте осуществлялась с использованием неокрашенной полиэтиленовой (ПЭТ) пленки толщиной 22±2 мкм. Вначале производилась регистрация энергетического спектра излучения гелий-неонового лазера, прошедшего через пленку. В эксперименте использовалась Фурье-преобразующая линза с фокусом 500 мм при диаметре освещающего пучка 11 мм. В дальнейших экспериментах эти параметры не менялись. Одна из реализаций пространственного энергетического спектра излучения гелий-неонового лазера, прошедшего через пленку, приведена на рис. 1. Хорошо видно, что ширина спектра меняется в зависимости от полярного угла, что свидетельствует о неизотропности свойств этой пленки. Анизотропия углового рассеяния вызвана визуально наблюдаемой полосчатой структурой пленки, которая обусловлена протягиванием пленки при ее производстве. Спекл-структура рассеянного лазерного излучения указывает на случайные фазовые искажения, вносимые образцом. Исследование пленки поляризационно-оптическим методом показало отсутствие двулучепреломления (поляризационных искажений).

Рис. 1. Изображение пространственного энергетического спектра излучения гелий-неонового лазера, прошедшего через пленку ПЭТ

Разумеется, такая среда и условия распространения излучения существенно отличаются от случайной среды, которая моделировалась в параграфе 1. Однако несмотря на это, как будет показано далее, основные закономерности, обнаруженные при моделировании, подтверждаются проведенными экспериментами. Кроме того, анизотропия свойственна некоторым природным явлениям (например, дождю, восходящим тепловым потокам воздуха), и в этом плане исследование, безусловно, полезно.

Для исследования устойчивости вихревых лазерных пучков Лагерра–Гаусса к действию случайной среды была собрана оптическая установка (рис. 2). Установка содержала гелий-неоновый лазер с линейно-поляризованным излучением, пространственный фильтр – расширитель пучка, ирисовую диафрагму (ИД), формирователь вихревых пучков Лагерра– Гаусса (ДОЭ), имитатор случайной среды – пленку ПЭТ, анализирующий модан (Модан), Фурье-преобразующую линзу (Л2) и ПЗС-матрицу.

В качестве анализирующего модана использовался многоканальный фазовый фильтр, согласованный с угловыми гармониками различных порядков [30, 31]. Такой элемент позволяет не только оптически детектировать топологический заряд вихревого пучка, но может быть использован для адаптивной компенсации смешения мод в волоконных телекоммуникационных системах [36].

Для формирования вихревых пучков Лагерра– Гаусса в эксперименте использовались соответствующие ДОЭ с несущей частотой [37, 38], работающие в первом порядке дифракции. Поэтому выходная часть оптической установки была установлена под углом к оптической оси и настроена на прием первого порядка дифракции. Пространственная фильтрация и расширение лазерного пучка до диаметра 25 мм осуществлялись объективом 20 × , точечной диафрагмой диаметром 15 мкм и линзой Л1 с фокусным расстоянием 200 мм. Размер пучка, освещающего ДОЭ, ограничивался до 11 мм ирисовой диафрагмой ИД. Исходное расстояние h 1 между формирующим ДОЭ и пленкой ПЭТ состав-

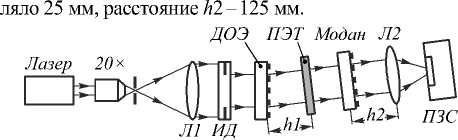
Рис. 2. Схема экспериментальной установки

В первом эксперименте исследовалось распространение искаженных вихревых пучков Лагерра– Гаусса в отсутствие Модана для n =0 и n = 2 (по аналогии с первыми двумя колонками табл. 1). Распределения интенсивности, зарегистрированные до и после прохождения пленки ПЭТ, показаны на рис. 3. Дискретизация вырезанных областей изображения одинакова и составляла 300×300 точек.

Результаты, приведенные на рис. 3, весьма сходны с результатами моделирования для n =0. Но для n =2 вид искаженных пучков несколько отличается от моделиро- вания, что можно объяснить существенными отличиями имитатора искажений в эксперименте от моделирования. Интенсивности искаженных пучков в эксперименте также мало менялись при перемещении пленки ПЭТ между ДОЭ и линзой Л2, как и интенсивности, показанные в табл. 1. Фазовые распределения в эксперименте не исследовались, но такое поведение интенсивности косвенно свидетельствует также о сходном поведении фазы в моделировании и эксперименте.

а)                        б)

Рис. 3. Распределения интенсивности пучков

Лагерра–Гаусса диаметром 11 мм до и после прохождения пленки ПЭТ толщиной 22 мкм: для n = 0

(верхние изображения) и n = 2 (нижние изображения)

Во втором эксперименте исследовалась обнаружительная способность используемой схемы детектирования вихрей. Измеренная интенсивность всех вихрей, кроме +1 порядка оказалась весьма мала и сравнима с интенсивностью шумов. В принципе это соответствует результатам моделирования, где интенсивность паразитных вихрей не превышала 4 %. Поэтому в дальнейшем в табл. 5–7 мы приводим только распределения интенсивности в порядке, соответствующем вихрю +1 порядка.

В табл. 5 приведены результаты исследования влияния расстояния h 1 между ДОЭ и пленкой ПЭТ (рис. 2). Расстояние h 1 изменялось в пределах 25– 225 мм. Используемая пленка ПЭТ имела незначительную толщину, поэтому ее перемещение не сопровождалось сдвигом изображения пучка.

Прежде всего, результаты исследования демонстрируют довольно сильную зависимость обнаружительной способности для вихрей первого порядка от расстояния ДОЭ – пленка ПЭТ. По-видимому, причиной этого является сближение случайной среды и анализирующего модана, в результате чего шумы с высокими пространственными частотами не успевают рассеяться, попадают на Модан и искажают результат. Иными словами, вихрь не успевает восстановиться на столь малом расстоянии. Кроме того, как уже говорилось, свойства пленки ПЭТ неизотропны, и влияние этого хорошо видно, особенно для n =0

(распределение интенсивности становится асимметричным). Однако это не приводит к каким-то существенным трудностям при обнаружении вихрей, и метод в целом показал хорошую устойчивость к изме- нениям свойств среды. Данные табл. 5 также показывают лучшую устойчивость вихревого пучка первого порядка при n =0, что полностью согласуется с результатами численного моделирования (табл. 2, 3).

Табл. 5. Распределения интенсивности в дифракционном порядке для n = 0 в зависимости от расстояния h1

	Без образца	h 1=25 мм	h 1=75 мм	h 1=150 мм	h 1=225 мм
n =0	•
n =2

Табл. 6. Дефокусированные изображения 1-го порядка при n = 2

h 1=25 мм	h 1=75 мм	h 1=125 мм	h 1=175 мм	h 1=225 мм

В определенной мере трудности при n =2 являются проблемой измерений, поскольку корреляционный максимум для n =2 существенно меньше по размеру, чем для n =0 и, соответственно, ближе по размеру к радиусу корреляции шума (рис. 1), что делает его менее устойчивым. Для уменьшения влияния этого фактора предлагается ввести небольшую дефокусировку в Фурье-плоскости при n =2, тем самым увеличив размер максимума и сделав его более заметным на фоне шумов. Соответствующие результаты приведены в табл. 6. Введенная дефокусировка составила около 40 мм. По сравнению с нижней строкой табл. 5 видно улучшение обнаружительной способности вихрей первого порядка. Для экономии места неискаженное изображение не приводится, а дано одно дополнительное искаженное. Корреляционный пик четко виден на всех расстояниях вплоть до 175 мм, в то время как в предыдущей серии он пропадал уже при 150 мм.

Заключение

Теоретически и экспериментально исследовано прохождение вихревых пучков Лагерра–Гаусса через случайную искажающую среду. Установлено численным моделированием и подтверждено экспериментально, что для вихрей низких порядков наилучшие результаты при прохождении через случайную среду дает мода низшего порядка. Теоретически показано, что для вих- рей высоких порядков применение многокольцевого пучка улучшает результат. Имитация случайной искажающей среды осуществлялась в эксперименте с помощью ПЭТ-пленки толщиной 22 мкм. Отличие свойств такого имитатора искажений от заложенных при моделировании не привело к существенному изменению основных результатов, связанных с влиянием порядка вихревых лазерных пучков Лагерра–Гаусса на сохранение топологического заряда вихрей. Это свидетельствует об устойчивости вихрей и измерительной системы к изменениям в искажающей среде. Экспериментально достигнуто некоторое улучшение обнаружительной способности пучков с вихрем первого порядка путем небольшой дефокусировки Фурье-каскада оптического коррелятора.

Работа выполнена при поддержке Министерства образования и науки РФ в рамках инициативного научного проекта по госзаданию 3.5319.2017/БЧ, а также Российского фонда фундаментальных исследований (грант РФФИ 16-47-630546 р_а).