Сравнение возможностей гистограмм и метода ранжированных амплитуд при анализе шумов однофотонных детекторов

Однофотонные детекторы на основе лавинных фотодиодов (ЛФД) активно применяются в локационных системах, квантовой оптике и коммуникациях [1]. Однако работу ЛФД в значительной мере осложняют темновые шумы, часть из которых (постимпульсные отсчёты) трудно устранить на практике [2]. Для характеризации работы ЛФД широко применяется ряд подходов [1], наиболее значимый из которых основан на построении гистограммы, редуцируемой из временных интервалов между отсчётами. При этом, в отличие от гистограммы, исходный набор временных интервалов содержит полную информацию о статистике отсчётов, необходимую для практического использования детектора.

В данной работе проводится сравнение метода гистограмм и метода последовательности ранжированных амплитуд (ПРА) [3] для количественной параметризации временных интервалов между темновыми отсчётами ЛФД. Метод ПРА уже демонстрировал свою эффективность при решении широкого круга задач дискретной статистики [4], возникающих в естественных науках. ПРА содержит в себе всю первоначальную информацию, полученную из исходного набора данных. На практике ПРА используется как промежуточное звено в построении гистограмм, в которых остаётся лишь часть исходной информации. Соответственно, метод, основанный на использовании ПРА, включает в себя всю информацию, которая используется в методе гистограмм. Ниже мы показываем, что метод ПРА позволяет намного быстрее характеризовать режим работы детектора, чем гистограммы, используя меньшую выборку данных.

1.    Метод ПРА

Последовательность временных интервалов между отсчётами детектора {xk} (k = 1, N ) всегда можно распределить (ранжировать) по убыванию замеренных интервалов и получить ПРА вида {sn} (s = 1, N ), где индекс n - порядковый номер уже в ПРА [3]. Очевидно, что по этому определению последовательность ПРА {sn} составлена ровно из тех же элементов, что и исходная последовательность {xk}, поэтому ПРА является неинвазивной (без потери информации) статистической количественной характеристикой выборки данных [4]. ПРА связана с функцией распределения F(xn, N) = F(sn, N) следующим приближённым соотношением (где N - размер выборки) [5,6]:

F ( s n , N ) = ( N + 1 - n ( s n ))/ N . (1)

Отметим также, что любые (даже негладкие и инфинитные) статистические функции (статистические средние по исходной выборке) от заданной выборки { x_k } и ПРА { s_n } строго совпадают. Математически это можно записать как условие

∑ k=! G (Xk ) = Z n=1 G (sn) = G [{sn}]

для любой функции G ( x ), что касается и гистограммы как функции выборки. Таким образом, ПРА является натуральным способом представления данных, который сохраняет всю статистическую информацию о выборке.

Более того, дальнейшие исследования показывают, что если вычесть среднее от исходной выборки, а затем проинтегрировать её ПРА, то получится колоколообразная кривая, которая, как показывают исследования, хорошо подгоняется функцией Jxn=A (xn-x0) a (xN-xn)e+B. Подгоночные параметры функции Jxn могут быть использованы для количественного описания случайных последовательностей без тренда, что с успехом было использовано в работе [7] для описания случайных флуктуаций расширенных временных рядов. Если возникает необходимость более детального описания, то после вычитания среднего значения можно разбить исходную ПРА на две (положительную и отрицательную) ветви и описать количественно каждую ветвь по отдельности с помощью полиномиальной функции с нецелыми показателями. Простейшая из них имеет вид Prn = A0 + A 1 x^' + A2x^2 +.... Эта идея была с успехом применена в работе [8]. Поэтому метод ПРА, как следует из вышеизложенного, является весьма перспективным и гибким статистическим методом, применимым для количественного описания случайных последовательностей самой широкой природы, не имеющих явно выраженного тренда. Причём заметим, что истинная гистограмма исходной последовательности остаётся неизвестной, так как соотношение (1) остаётся приближённым, что подтверждается предыдущими исследованиями [5] и результатами этой работы при сравнении формулы (1) с реальными данными.

Гистограмма по своему определению приближается к плотности вероятности р ( x ) = d f /d x с ростом N , оставаясь инвазивной и не гладкой функцией (гладкость увеличивается с ростом N ), зависящей от способа разбиения данных выборки. Шумы источников света и темновые шумы, соответствующие пуассоновским процессам [1], имеют плотность вероятности р ( x ) для временных интервалов « x » между ближайшими отсчётами, описываемую распределением d f /d x = р ( x ) = % exp (- % x ), где % - средняя частота фиксируемых событий. Для пуассоновских процессов ПРА описывается формулой [6] s n = % ^-1ln ( N/ n ), имеющей один свободный параметр % . Для произвольного случая функция F ( x n , N ) может быть найдена из общего выражения (1).

2.    Сравнительный анализ ПРА и гистограмм

Количественный анализ устойчивости метода к изменению размера выборки можно провести на основе коэффициента детерминации R2 [4] или нормированной меры совпадения. Для Q подвыборок {xq,k} длины N, где q = 1, Q, к = 1, N , {yk} = {Q У Q x,} -^■^е q = 1 q , усреднённая выборка, y = N-1 У N=1 yk - полное среднее, относительный квадратичный (R2-подобный) коэффициент отклонения вида

е ( ^N ) = Q - ¹ У N = 1 У Q . , ( x q , к - У к )²/У N = 1 ( У к - У )² (2)

позволяет сравнить набор ПРА SPA [{xq,k}] длины N с набором гистограмм Hist[{xq,k}] (m = 1, Nh) оптимальной длины [11] Nn(N) = [4(3(N – 1)2 / 4)1/5]div[1] (критерий Манна–Вильда). При этом очевидно, что Hist[{xq,k}] = HistSPA[{xq,k}]] и гистограмма является функцией уже только от ПРА и ПРА полностью включает гистограммы. Этот факт говорит о том, что из гистограмм по определению невозможно получить больше информации, чем из ПРА. И наоборот, ПРА содержит всю информацию о гистограмме. Ниже мы анализируем интервалы между темновыми отсчётами однофотонного детектора. Для эффективности детек- тора ID210 (ID Quantique) 15 % и мёртвого времени 24 µs была экспериментально получена выборка общей длины 105 точек. Из этой выборки формировался набор из Q = 100 подвыборок длины N =20j (j = 1,50). Вычисляя отклонение е из (2) для каждого N, в случае ПРА и гистограмм, соответствующих одинаковым подвыборкам, получим графики, изображённые на рис. 1.

е

0,6

0,5

0,4

0,3

0,2

0,1

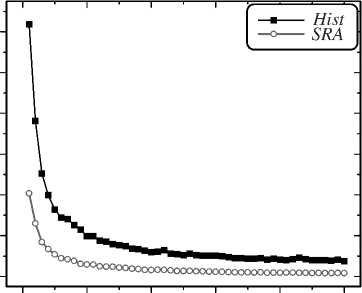
0    200   400   600   800 N

Рис. 1. Зависимость отклонения £ от N для ПРА (SRA -серые кружки) и гистограмм (Hist – чёрные квадратики)

Как видно из рис. 1, величина отклонения ε (N) значительно меньше для метода ПРА, чем для гистограмм для любых значений N: е (103) = 0,0369 для гистограммы и е (103) = 0,0078 для ПРА, то есть отклонение е оказывается в 4,7 раз меньше соответственно. Большое качественное различие наблюдается также и для других способов выбора параметра разбиений Nh(N) в силу того, что гистограмма даже с максимальным параметром разбиений Nh (N) = N/ 10 (см. критерии в [11]) сокращает количество данных в статистическом анализе с N до N/ 10 точек, что обуслав- ливает принципиальную инвазивность метода гистограмм. Существенным недостатком гистограмм, по сравнению с ПРА, является их зависимость от Nh (N) (см. рис. 2).

Hist

Nh=ll Nh=60

Normalized histogramm Hist(z).

^— ^*(x-X/J,/f7)/(x„MY-X„2/77)

N=1000

4-

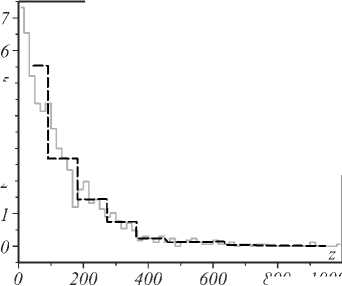
800 1000

Рис. 2. Нормированные гистограммы Hist(z), z = N(x–x min ) / (x max –x min ), для первой подвыборки {x k } из рис. 1 для N_h = 11 (чёрная пунктирная кривая, критерий Стерджесса) и N_h = 60 (серая кривая, критерий Манна – Вильда) (более оптимальное разбиение)

^1

Отметим, что выбор оптимального значения Nh(N) не определяется универсальными критериями и явля- ется отдельной проблемой для каждой конкретной физической задачи [11]. Для выборки с N = 103, соответствующей рис. 2, и теоретической подгоночной кривой ρ(x) = λexp(–λx) для пуассоновских процессов, описанных выше, мы имеем меру отклонения 1– R2 = 0,0125 для оптимальной нормированной на среднее гистограммы (Nh =60, рис. 2) и 1–R2 = 0,0043 для нормированного на среднее ПРА (R2 – коэффициент детерминации [4]).

То есть доля ошибок в задаче описания данных при использовании ПРА оказывается примерно в 3 раза меньше. Другим преимуществом ПРА по сравнению с гистограммами [3, 4] является выигрыш по скорости характеризации статистики отсчётов, что открывает важные перспективы внедрения метода ПРА в программное обеспечение высокочувствительной измерительной техники.

Заключение

Количественное сравнение методов гистограмм и ПРА демонстрирует значительные практические преимущества последнего метода для быстрого статического анализа шумов однофотонных детекторов благодаря возможности использования коротких выборок экспериментальных данных. Показано, что в этом случае метод ПРА содержит в себе всю информацию, которую можно получить с помощью метода гистограмм. В силу неинвазивности метод ПРА также применим в области идентификации различных источников сигналов [4, 10, 11] и шумов [6]. Продемонстрированные преимущества указывают на перспективы использования метода ПРА для высокоточной характеризации шумов однофотонных детекторов, что необходимо для проведения экспериментальных работ в области квантовой оптики, оптических квантовых вычислений и квантовых коммуникаций.

Исследования шумов в области фотоники и квантовых технологий были поддержаны грантом Правительства Российской Федерации, проект № 14.Z50.31.0040, 17 февраля 2017 г. (теоретическая часть). Работа также частично поддержана грантом РФФИ 16-32-60054 мол_а_дк (экспериментальная часть).