Сравнительная оценка адаптивности сетей с помощью перегруженных связей на примере цепочки отображений

Предметом исследования является адаптивность сетей в широком смысле. Под адаптивностью понимают свойство сети сохранять устойчивую динамику при наличии негативных факторов. Например, при обрыве некоторых связей, отключении нескольких узлов, зашумлении канала связи. При этом обычно полагают, что адаптивность не зависит от физической природы узлов сети, является характеристикой сетевой топологии. Поэтому имеет смысл говорить не об адаптивности какой-то конкретной сети, а всех сетей с топологией А. В дальнейшем для краткости вместо «произвольная сеть с топологией А» будем использовать «сеть А» или «топология А».

Предполагается, что топология А допускает матричную формализацию, то есть представима в форме матрицы N х N , где N - число функциональных узлов в сети. При этом имеет значение только наличие или отсутствие связи между парой элементов и направленность связи (симметричная или однонаправленная). Запаздывание, физическая реализация, асинхронность и другие характеристики связей игнорируются.

Также предполагается, что узлы сети равноправны: то есть у сети нет управляющего узла (базовой станции) или управляющий узел вынесен из рассмотрения. Такие сети представляют особый интерес с точки зрения адаптивности, самоорганизации и самоопти-мизации [1–3].

Независимо от теории сетей исследуется другой предмет: ансамбли логистических отображений с перегруженными связями. Определение перегрузки будет дано ниже. Хаотические ансамбли относятся к предметной области нелинейной динамики. Их изучение имеет самостоятельную теоретическую ценность в рамках теории хаоса. Однако, как выяснилось [4], ансамбли с перегруженными связями являются удобным инструментом для оценки адаптивности сетевых топологий.

Хаотический ансамбль размерности N – это динамическая система, составленная из N более простых динамических систем (т.е. элементов), связанных между собой. Как правило, элементы одного ансамбля имеют схожую структуру. Ансамбль допускает простейшую декомпозицию, то есть переход к N независимым динамическим системам. В этом случае элементы называют парциальными системами. Траектории (поведение) парциальной системы называют парциальной динамикой.

Элементами хаотического ансамбля могут быть одномерные или многомерные системы, с непрерывным или дискретным временем. Однако большинство свойств и эффектов коллективной динамики ансамбля не зависит от конкретного вида элементов ансамбля. Например, в [5–10] полученные результаты схожи для кусочно-линейного отображения, логистической параболы и системы Курамото.

Слабая зависимость коллективной динамики от парциальной динамики методологически сближает ансамбли и сети, позволяет использовать их для взаимного моделирования. Кроме того, можно получить достаточно сложную управляемую динамику, соединяя простые и хорошо изученные нелинейные элементы. Например, динамика автономного логистического отображения детально изучена как численно, так и теоретически. Логистическое отображение используется, как правило, для демонстрационных (обучающих, иллюстративных) целей или как инструмент предварительного исследования более сложных систем. Поэтому во всех дальнейших выкладках будет использоваться именно ансамбль логистических отображений.

Полученные практические результаты, возможно, допускают обобщение на ансамбли с произвольными парциальными элементами. Однако цель исследований – изучение не хаотических ансамблей самих по себе, а исследование сетевых структур с помощью хаотических ансамблей. Это значит, что нет смысла усложнять или обобщать хаотический ансамбль, если его максимально простая конфигурация позволяет эффективно моделировать произвольные сети и оценивать их адаптивность.

2.    Модель

Динамика ансамбля полностью определяется тремя объектами: матрицей связей А, вектором парциальных параметров р, вектором начальных условий x0. Эволюция состояния ансамбля на каждой итерации описывается N-мерным преобразованием вида где f – N -мерная логистическая вектор-функция f (Zi)= piZi(1 - Zi).                                     (2)

Заметим, что при декомпозиции (замене А на единичную матрицу) вектор-функция вырождается в систему из N независимых парциальных логистических отображений.

Матрица связей А содержит весовые коэффициенты для нахождения так называемого среднего (или средневзвешенного) поля:

N

Z i = ^^ A ij x j ,                                    (3)

j =1

то есть коэффициент A ij определяет относительное влияние состояния элемента j в текущий момент времени на эволюцию элемента i (в следующий момент времени). Диагональные элементы матрицы называются коэффициентами самовоздействия .

Матрица связей должна удовлетворять двум дополнительным требованиям. Во-первых, это нормировка на единицу:

N

^ A ij = 1 Vi = 1 ^ N,                           (4)

j =1

во-вторых, достаточное условие финитной динамики:

0 ^ A ij <  1 .                                          (5)

Выполнение условия (5) гарантирует, что ни один элемент ансамбля не покинет заданную область. В случае логистических ансамблей значения всех отображений в любой момент времени лежат в единичном интервале.

Введем понятие структурного сопряжения (Кап). Пусть имеется сеть А, содержащая N однотипных узлов, и задано матричное представление топологии А. Пусть имеется ансамбль из N элементов с матрицей связей B. Назовем сеть А и ансамбль B структурно взаимосопряженными, если sign( Aij )=sign( Bij)                                 (6)

и

A ij = A ji < = > B ij = B ji .                             (7)

Фактически структурное сопряжение требует только сохранения структуры связей. Природа узлов сети, асинхронная передача данных и другие сетевые особенности не учитываются. В данной статье, как и в [2], перегрузка в ансамблях используется для моделирования негативного воздействия на сеть. При этом использование хаотических ансамблей позволяет абстрагироваться от конкретной природы негативных факторов.

Покажем на примере простейших сетей с линейной и кольцевой топологией, как оценивать общую адаптивность с помощью перегрузки соответствующих ансамблей.

Модель представляет собой цепочку N логистических отображений. Рассматриваются две топологии: простая цепочка, простое кольцо; два случая связей: однонаправленные и симметричные. Всего четыре топологических класса. Замкнутая цепочка является кольцом порядка 1 (простым кольцом), где каждый элемент связан только с двумя ближайшими соседями. Кольца более высокого порядка и их превращения в сеть малого мира рассмотрены в [2, 11].

Соответствующие матрицы связей имеют вид

.

.

.

A 00 =

a

-

a

.

.

.

A 10 ⁼

V

.

.

.

-

a

a

.

.

.

.

-a

.

.

.

.

.

.

.

.

.

.

.

.

a

.

.

.

.

.

.

.

,

-

a/

a 0

.

.

,

.

.

.

.

.

.

A 11 =

A 21 ⁼

- a/ 2	. . 0 a/ 2	. . 0 . ...	..   . ..   . .. a 1 00	a	0	⎞
a/ 2	1 -a	a/ 2	...     0		0
0 .	a/ 2 .	1 -a .	...     0 ..		0 .
. . 0	. . 0	. . 0	.. .. ... 1 -a		. . a/ 2    ⎟
0	0	0	... a/ 2	1 - a/ 2
⎛ 1 -a	a/ 2	0	...    0	a/ 2 ⎞
a/ 2 .	1 -a .	a/ 2 .	...    0 ..	0 .		.
. . a/ 2	. . 0	. . 0	.. .. ... a/ 2	1	. . a

,

Нижние индексы у матриц введены из соображений классификации сетей по минимальной силе узлов и структуре обратных связей. В дальнейших работах этот вопрос будет раcкрыт более полно. Сейчас отметим только, что первый нижний индекс – это минимальное количество исходящих связей у узлов сети, второй индекс – наличие обратных связей.

3.    Оценка адаптивности с помощью перегрузки

В отличие от классических методов, где для оценки адаптивности вносятся изменения в топологию (удаляют некоторые связи или узлы), в предложенном методе структура связей постоянна. Предлагается моделировать негативные сетевые факторы с помощью чисто количественного преобразования – перегрузки.

Перегрузкой связи называется преобразование L матрицы связей А , которое увеличивает некоторые (как правило, наперед заданные) ненулевые недиагональные элементы А , нарушая условие (5), но сохраняя нормировку (4). Выбор связей, подвергаемых перегрузке, зависит от задач моделирования и особенностей моделируемого объекта. Последний представляет собой сеть с линейной или простейшей кольцевой топологией. Достаточно обрыва хотя бы одной связи (выключения хотя бы одного узла), чтобы сеть потеряла свои топологические свойства. Поэтому целесообразно ввести перегрузку всего одной связи. Введем перегрузку l как преобразование матрицы А :

l : A 21 → A 21+1 + l + 1 , A 22 → A 22 _- 1 - l - 1 . (12)

Как показано в [12], перегрузка приводит к появлению бассейна инфинитной динамики. Если точка принадлежит такому бассейну, то проходящая через нее траектория уходит на бесконечность. С ростом перегрузки бассейн инфинитной динамики разрастается, заполняя весь единичный гиперкуб. В этом случае говорят о полном разрушении динамической системы.

Для оценки адаптивности используются два количественных показателя: критическая перегрузка (необходимая для полного разрушения) и чувствительность ансамбля А к перегрузке. Последняя более информативна, так как связана со структурой связей. Грубо говоря, адаптивная структура лучше «перераспределяет» перегрузку, тем самым замедляя процесс разрушения. Для оценки чувствительности ансамбля используется вероятность финитной динамики. В данной работе оценка вероятности финитной динамики осуществляется с помощью численных экспериментов.

Вероятность финитной динамики w a ( l ) систем с матрицей связей А при перегрузке l оценивается следующим образом. Фиксируется матрица связей А и величина перегрузки l. Вектор начальных условий x 0 выбирается случайно (равномерно) внутри единичного гиперкуба. Значения парциальных параметров в столбце p также выбираются случайно (равномерно) из отрезка 3 С п С 4. Осуществляется достаточно большое число итераций. Эксперимент считается успешным, если в течение всего итегрирования траектория системы ни разу не покинула окрестность нуля заданного радиуса.

Проводится несколько тысяч экспериментов с разными случайными начальными условиями и разными случайными параметрами. Данная модель использует фиксированное (не случайное) расположение связей, поэтому повторная генерация матрицы связей в рамках одной серии экспериментов не требуется в отличие от [2], где связи каждый раз располагаются случайным образом.

Подсчитывается доля успешных экспериментов. Полученный результат и является оценкой вероятности финитной динамики w a ( l ). Нижний индекс означает, что вероятность относится ко всем системам с матрицей связей А и не зависит от конкретного значения параметров и конкретных начальных условий.

4.    Замечание

Чем больше итераций, тем точнее результаты. Для первичной оценки достаточно порядка сотни итераций. Установлено, что оптимальным является число итераций на полтора порядка больше, чем число элементов в ансамбле. Дальнейшее увеличение числа итераций существенно не влияет на результаты. То же касается радиуса окрестности нуля, выход из которой означает инфинитную динамику. Так как уход на бесконечность происходит экспоненциально, то увеличение радиуса отдаляет выход из окрестности всего на несколько итераций. Поэтому нет особого смысла использовать окрестность слишком большого радиуса. С другой стороны, в [2, 12] перегруженное отображение часто заходило в отрицательную область, сохраняя финитную динамику. На этом основании используется окрестность нуля единичного радиуса.

5.    Результаты

Результат каждой серии численных экспериментов представялет собой зависимость w a ( l ) для ансамбля фиксированного размера. На рис. 1 представлены графики w a ( l ) для цепочек с числом узлов от 2 до 15. Для удобства восприятия область значений ограничена от 0.25 до 0.75, вне этой области графики медленно прижимаются к уровню 0 и 1 соответственно. Напомним, что согласно [2] нас интересует только линейный участок графика.

Видно, что графики для коротких цепочек качественно отличаются от цепочек с N >  5. Более точные вычисления, без искусственного ограничения области значений, дают значения N >  8, хотя для восьми узлов незначительным возмущением адаптивности уже можно пренебречь (рис. 2). Для них метод прямой оценки адаптивности неприменим. Возможно, здесь актуален другой метод, основанный на анализе бифуркационных диаграмм [2], но это выходит за рамки настоящей статьи.

Напомним, в матрицах (8–11) связь a может принимать значения из единичного интервала. Изменение этой «фоновой» влияет на характер разрушения коротких цепочек (рис. 3). Если сравнить оба семейства графиков, то видно, что уменьшение фоновой связи при постоянной длине цепочки эквивалентно увеличению длины цепочки при постоянной фоновой связи. Это позволяет предположить, что впоследствии мы сможем рассматривать не отдельно два параметра (фоновую связь и число узлов), а некоторую их комбинацию.

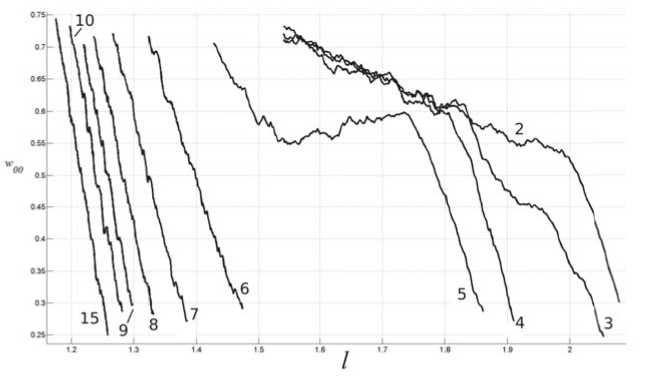
Рис. 1

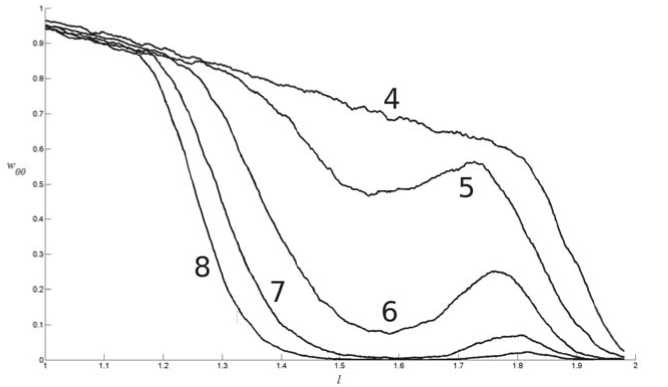
Рис. 2

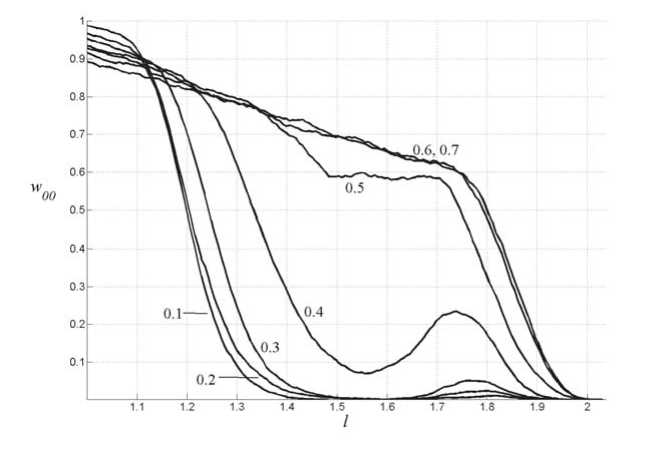
Рис. 3

Однако на данном этапе в этом нет необходимости, так как нас интересуют не абсолютные количественные характеристики, а их отношения между собой. Например, если требуется сравнить адаптивность двух сетей, то достаточно исследовать их графики w _a ( l ) при фиксированном а.

Кроме того, у этого результата есть одна простая интерпретация: чем длиннее цепочка, тем «дальше» (в информационном плане) её концы друг от друга. И вообще среднее расстояние между двумя случайными звеньями увеличивается. Ослабление фоновых связей между звеньями эквивалентно их взаимному отдалению, то есть увеличению «эффективной длины» цепочки.

Далее, на рис. 3 видно, как линейные участки графиков при а = 0 . 1 , 0 . 2 , 0 . 3 практически сливаются. Можно предположить, что при любой фиксированной фоновой связи тот же эффект будет иметь место для достаточно больших цепочек.

Действительно, с увеличением N угловой коэффициент линейных участков действительно стремится к предельному значению (рис. 4). Более того, графики для разных достаточно больших N сливаются вплоть до неразличимости. Начиная с N =15, можно с хорошей точностью считать, что линейные участки совпадают. Этот результат не зависит от фоновой связи. То есть к изменению фоновой связи чувствительны только короткие цепочки. Для длинных цепочек «эффект насыщения» (существование предельной скорости разрушения) сохраняется. Более того, при разных значениях фоновой связи предельная скорость составляет K 0 0=9 ± 0 . 5. Погрешность можно уменьшить путём увеличения экспериментов в серии и числа итераций в каждом эксперименте. Однако на данных такая точность представляется избыточной.

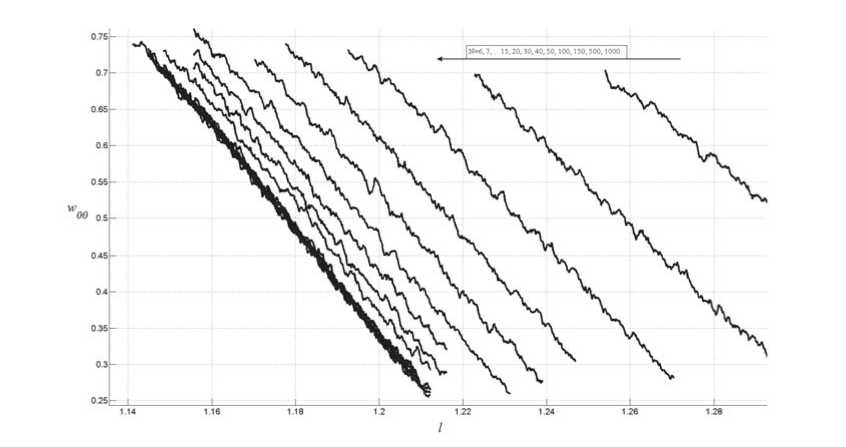
Рис. 4

Также при всех значениях фоновой связи имеет место соотношение

N lim ∼ 2 N 1 .                                   (13)

где N 1 – максимальная длина малой цепочки, то есть самой длинной цепочки с выраженным локальным максимумом, N _lim – минимальная длина большой цепочки, то есть число узлов, когда линейные участки графиков уже неразличимы. Например, для a = 0.4, N li_m = 15, N 1 = 7.

Аналогичным образом исследована цепочка с симметричными ( A 12 ) связями и простые кольца с однонаправленными ( A 10 ) и симметричным ( A 21 ) связями. Для всех этих топологий также существует предельная скорость разрушения. Также при различных значениях фоновой связи имеет место следующее выражение:

K 00 10 11 < K 21 ,

Имеется существенное отличие результатов остальных трёх топологий от однонаправленной цепочки. А именно, уже начиная с трёх узлов, все графики имеют ровно один выраженный линейный участок без возмущений. Кроме того, выход на предельное значение углового коэффициента происходит в три раза быстрее: 5 узлов против 15 у цепочки (рис. 5) при фоновой связи a = 0 . 4. Зависимостей w a ( l ) с локальными максимума не обнаружено. Этот результат требует дополнительного обсуждения.

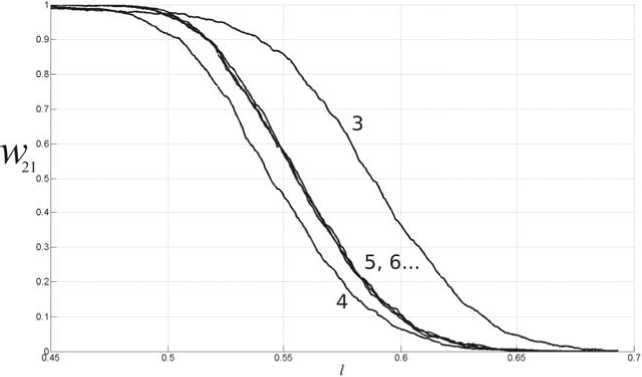
Рис. 5

6.    Анализ результатов. Классы адаптивности и разрывов

Качественное изменение зависимости w a ( l ) с ростом N указывает на наличие скрытых подклассов внутри одного топологического класса. Уместно (в шутку) вспомнить старую философскую дилемму: «сколько песчинок песка образуют кучу?». Длинные цепочки – это такие, у которых график w a ( l ) не имеет локального минимума и у которого только один выраженный линейный участок. То есть цепочки с более чем шестью узлами являются длинными.

Наличие локального минимума можно интерпретировать как преимущество в адаптивности. В самом деле, вопреки возрастанию перегрузки, сеть демонстрирует парадоксальное возрастание «запаса прочности». Таким образом, логично ввести понятие класс адаптивности , принадлежность к которому определяется по качественному виду зависимости w a ( l ), по скорости разрушения и (например) по виду бифуркационных диаграмм [2]. Не исключено, однако, что в класс адаптивности «коротких цепочек» попадёт сеть с более сложной топологией T . В рамках нашей концепции это будет означать следующее: сеть T можно заменить на цепочку из пяти элементов без потери адаптивности.

В этом смысле нет нужды количественно сравнивать адаптивность коротких и длинных цепочек – это принципиально разные (с точки зрения адаптивности) классы. Короткие цепочки являются качественно более адаптивным, чем длинные. Дело не только в вероятности разрыва цепи в произвольном узле.

Мы предлагаем различать разрывы разной степени «фатальности», или топологической необратимости, выделить тот случай разрывов, когда сеть хоть и распадается на несколько сетей, но каждая новая сеть принадлежит к тому же классу адаптивности. Так, короткая цепочка распадается на две сети, но обе новых сети – это снова короткие цепочки. Если предположить, что сети из одного класса взаимозаменяемы, то мы только «выиграли» от такого разрыва, потому что получили дополнительную сеть.

С другой стороны, цепочка из двух элементов распадается всегда в пару одиночных элементов, которые уже нельзя считать цепочками. Поэтому и график w a ( l ) для N = 2 не имеет локального минимума, а, напротив, демонстрирует ещё более быстрый распад динамики. Поэтому пару элементов можно выделить в отдельный класс адаптивности («два элемента – ещё не цепочка») или рассматривать как вырожденный случай коротких цепочек.

Длинная цепочка при произвольном разрыве распадается либо на две коротких, либо на короткую и длинную, либо на две длинных. Однако распад на две короткие возможен только при количестве узлов, меньшем 2 N 1 , поэтому дальнейшее увеличение цепочки уже не влияет на адаптивность, что подтверждается соотношением (13). В самом деле, любой распад цепочки N > N _lim породит хотя бы одну длинную цепочку.

Из этих же соображений несложно проинтерпретировать неравенство (14). Так, разрыв в цепочке ведёт к образованию двух цепочек – топологический класс не меняется (падает только мощность сети). Разрыв в кольце превращает кольцо в цепочку, то есть необратимо меняет топологический класс. Поэтому простое кольцо менее адаптивно, чем простая цепочка.

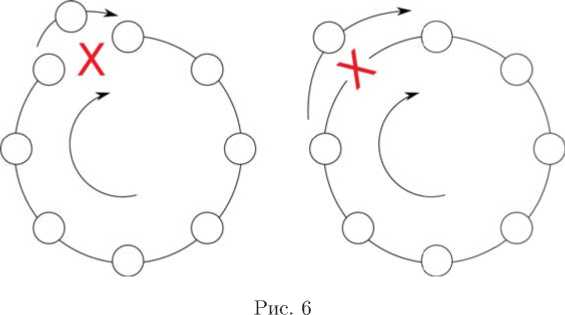
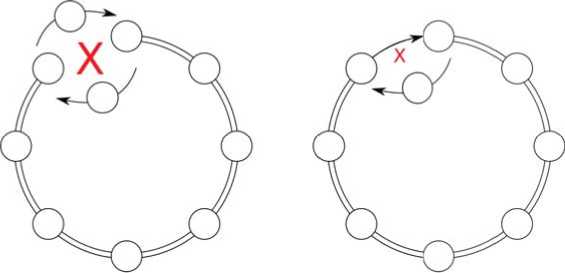
Рис. 7

Однако разрыв в кольце и в цепочке можно устранить, добавив так называемый простой компенсатор. Это узел, имеющий ровно одну входящую и ровно одну исходящую связи. Притом неважно, это разрыв связи или выход из строя узла (рис. 6). В моделях адаптивных активных беспроводных сетей, как правило, предполагается, что мы располагаем большим количеством равноправных узлов, в том числе находящихся в режиме ожидания.

Как нетрудно догадаться, одного компенсатора недостаточно для восстановления топологии при отключении узлов в любой сети с обратными связями. При разрыве симметричной (двойной) связи также требуется два компенсатора. Если разрывается только одно направление симметричной связи, то компенсатор вносит принципиальную асинхронность (задержку) в сеть (рис. 7). То же справедливо для цепочки.

Кроме того, разрыв симметричной связи в кольце превращает кольцо в симметричную цепочку, то есть меняет топологический класс. Разрыв же в симметричной цепочке ведёт к образованию двух симметричных цепочек. Поэтому симметричная цепочка более адаптивна, чем симметричное кольцо. С другой стороны, разрыв только одной связи (из симметричной пары) искажает топологию симметричной цепочки, поэтому симметричная цепочка менее адаптивна, чем простое кольцо. Простое кольцо менее адаптивно, чем простая цепочка (см. выше). Таким образом, соотношение (14) полностью проинтерпретировано.

Может показаться странным: почему наименьшей адаптивностью обладает симметричное кольцо? Ведь разрыв одной связи в симметричном кольце всего лишь замедляет распространение информации в одну сторону (в N раз). В то же время разрыв одной связи в цепочке разделяет её на две части. Напомним, что с самого начала перегрузка какой-либо связи не рассматривалась как вероятность разрыва именно этой связи. Перегрузка моделирует влияние негативных факторов на сеть в целом. Что же касается разрывов, то здесь важна не только целостность сети, но и сохранность топологии.

Наличие обратных связей при наличии сильных негативных факторов только усугубляют распространение ошибок. Если при однонаправленной связи вышел из строя потенциальный получатель сигнала, отправитель сигнала продолжит свою работу. Если подобное случается в симметричной цепочке (или кольце), то отправитель будет ждать отчёта от получателя, тем самым затормозит работу всей сети.

Также в основной функционал активных адаптивных сетей не входит передача данных из одной точки в другую. Ценность этих сетей – именно в распределенном принятии решений и в способности сохранять структуру после отключения ряда узлов, пусть и в меньшем масштабе. В конце концов, сохранение локальной целостности при нарушении целостности глобальной – одно из проявлений адаптивности.

Метод сравнительной адаптивности с помощью перегрузки позволяет избежать этих дополнительных рассуждений.

7.    Вывод

Основным результатом является применимость метода для сетей простейшей топологии. Метод устойчив относительно изменения параметров хаотического ансамбля (набор парциальных параметров, начальные условия, фоновые связи, число узлов). Таким образом, зависимость разрушения динамики от перегрузки является универсальной в рамках одного топологического класса. Далее, для разных топологических классов наблюдается общность в характере разрушения. А именно, на всех (может быть, за исключением конечного числа) графиках w(l) существует линейный участок. Для рассмотренных топологий существует предельное значение углового коэффициента линейного участка. То есть для достаточно больших сетей адаптивность уже не зависит от дальнейшего разрастания сети. Кроме того, сравнение предельных угловых коэффициентов позволяет сравнивать адаптивности разных топологий. В частности, удалось упорядочить рассматриваемые топологии в порядке уменьшения адаптивности: короткая цепочка, длинная цепочка, простое кольцо, цепочка с симметричной связью, кольцо с симметричной связью.

Работа выполнена при поддержке РФФИ в рамках проекта 17-07-00815 А.