Сравнительная оценка качества управления асинхронным электроприводом конденсатного насоса с подчиненными и модальными регуляторами

Sibirskii Gosudarstvennyi Aerokosmicheskii Universitet imeni Akademika M. F. Reshetneva. Vestnik Vol. 17, No. 2, P. 423–430

COMPARATIVE EVALUATION OF QUALITY OF CONTROL OF ASYNCHRONOUS ELECTRIC CONDENSATE PUMPS WITH SUBORDINATE AND MODAL CONTROLLERS

• A. N. Pakhomov, M. F. Korotkov ^* , A. A. Fedorenko

Siberian Federal University

• 79, Svobodny Av., Krasnoyarsk, 660041, Russian Federation

• ^*E-mail: hamsterboo@mail.ru

The subject of the study includes dynamic characteristics of variable frequency induction motor with a modal control.

The topic of research that received the greatest distribution system transmitter frequency with independent voltage inverter with pulse-width modulation is an asynchronous motor.

The purpose of the work is to study the dynamic properties of the actuator with a modal control, as well as recommendations for the practical use of engineered control systems.

In our research work we used the following methods. To solve the given problem the modern theory of electric, the theory of automatic control, the continuous Laplace transform, the method of transfer functions and state space by standard polynomial equations were used. Experimental study of the results obtained theoretically was held by mathematical modeling in time field using personal electronic computer.

As a result, the analysis of the work of the modal systems and slave control of asynchronous electric motor as an example of the condensate pump is given. The estimation of the quality control processes of coordinates by analyzing the results of simulation system in the medium MatLab is given.

The results can be applied in the system of variable frequency drive with more controlled output coordinates, for example, robotic machines and devices, electromechanical systems and other space vehicles.

In the work the comparative analysis of systems and subordinate modal control is given. It was found that the benefits of the use of modal regulators compared to the same regulators built on the principle of subsidiarity control, is that:

• a)    consideration of the frequency control system with induction motormodal regulator has approximately twice the speed compared with those of a subordinate authority;

• b)    the modal regulators have greater noise immunity and are less sensitive to changes in the internal parameters of the motor, compared with controls built on the principle subordinate regulation;

• c)    the stiffness of the mechanical characteristics of the drive system with a closed modal control is significantly higher than in the system with the slave control.

Введение. Теория систем векторного подчиненного управления частотно-регулируемого асинхронного электропривода (АЭП) разработана достаточно полно [1—9]. Однако вопросы синтеза модальных регуляторов рассматриваются, как правило, для электроприводов постоянного тока. В связи со сложившейся тенденцией в различных отраслях промышленности, в том числе ракетно-космической отрасли, повсеместного перехода на АЭП, целесообразно рассмотреть применение модального управления для повышения грубости системы электропривода переменного тока к вариациям параметров. В работе проведен сравнительный анализ систем модального и подчиненного управлений асинхронным электроприводом. В литературе [10] отражены результаты экспериментальных исследований, подтверждающие достоверность результатов математического моделирования [11-13] систем подчиненного управления асинхронным электроприводом. Основываясь на этом, при моделировании системы с модальным регулятором в качестве базовой используется модель частотно-управляемого асинхронного электропривода [8; 9] с подчиненным регулированием переменных, в которой регуляторы подчиненного управления заменены модальным регулятором. Очевидно, что результаты математического моделирования такой системы будут соответствовать результатам физического эксперимента.

В работе проведено исследование переходных процессов в замкнутых системах асинхронного электропривода при подчиненном и модальном управлении. Нагрузку на двигатель формирует конденсатный насос.

Математическое описание объекта управления. На рис. 1 приведена функциональная схема замкнутой системы асинхронного электропривода конденсатного насоса. Она состоит из блока регуляторов (БР), блока компенсаций (БК), прямого и обратного преобразователя координат (ПКП, ПКО), ПЧ, блока вычисления модуля потокосцепления (МП) [14], электродвигателя и насоса. Назначение и реализация блоков БК, ПКП, ПКО приведены в [8; 9; 15].

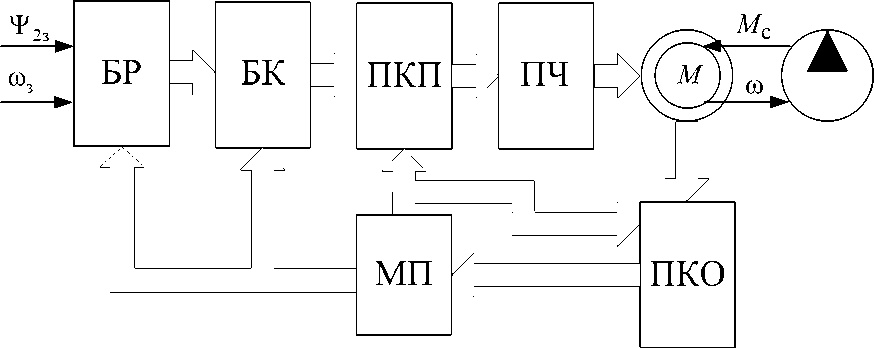
Рис. 1. Структурная схема системы электропривода

Преобразователь частоты с автономным инвертором с широтно-импульсной модуляцией формирует не только частоту, но и амплитуду выходного напряжения, влияние звена постоянного тока на динамические свойства системы при синтезе можно не учитывать. Кроме того, частота модуляции современных преобразователей весьма высока, что позволяет пренебречь также его дискретными свойствами. Изложенное позволяет представить в первом приближении преобразователь частоты безынерционным линейным звеном с коэффициентом передачи k _п.

Математическая модель АД в форме Коши с учетом общепринятых допущений в декартовой системе координат u - v , вращающейся с произвольной скоростью го _k , имеет вид [9; 16]

di1 u = dt	1 Ц» - R T , 1 u	1 .         k 2 + Т э 1 u  T 2 R T 3	^ 2 u + p2 P T 1 го ^ 2 v + го k i 1 v ; R Т э
di1 v = dt	1 -----u\y -R э T 1 v	1 .          k 2 + Т э 1 v T 2 R Т э	^2v- kp - го^2м- гок i „; 2 v    ту rp       2 u      k 1 u 7 R Т э
d ^ 2 u dt	= R 2 k 2 i 1 u	-™X^2 u + (го k T 2	- P п го) ^2 v ;

= R 2 k 2 h v - V ^ 2 v - (го k - P п ГО) ^ 2 u ;

T 2

d го dt

³P п k 2

2 J

i 1 v ^ 2 u

³ P п k 2

2 J

i 1 u * 2 v

J ^M = ’

где u i „ , u i v , i i u , i 1 v , ^ 2 u , ^ 2 v - проекции на оси u и v

декартовой системы координат результирующих

векторов напряжения статора u ₁ , тока статора i ₁,

потокосцепления ротора Т₂ соответственно; го -угловая скорость вращения ротора; го _k - скорость вращения системы координат u - v ; M _; - момент статического сопротивления на валу двигателя; р _п -число пар полюсов; J - момент инерции механической части привода; T _э и R _э - эквивалентные электромагнитная постоянная времени и активное сопротивление цепи статора АД; T ₂ и R ₂ - активное сопротивление и электромагнитная постоянная времени цепи ротора АД; k ₂ - коэффициент

электромагнитной связи ротора АД. Выражения для расчета параметров двигателя можно найти в [8; 9].

Синтез регуляторов производится отдельно для двух каналов управления: канала регулирования потокосцепления ротора АД и канала регулирования скорости АД.

Быстродействующие токовые контуры реализованы во вращающейся синхронно с магнитным полем машины системе координат x - у . Переход от системы координат u - v к системе x - у осуществляется с помощью ПКП и ПКО.

Настройка токовых контуров производится без учета влияния перекрестных связей. Некомпенсируе-мая постоянная времени, определяемая инерционностью и временем чистого запаздывания ПЧ, наличием фильтров в каналах регулирования и дискретностью АИН, принята равной T _u = 3,5 мс.

Настройка каналов регулирования потокосцепления и скорости ротора осуществлена на модульный оптимум и биномиальное разложение соответственно. Согласно [8], при Тл = 3,5 мс время переходного процесса подсистемы стабилизации |т2| при настройке на модульный оптимум равно tпп^2 = 4,14ТЦ = 14,49 мс, (1)

а подсистемы стабилизации скорости при биномиальной настройке:

t ппго = 4,74 Т _ц = 16,59 мс. (2)

Синтез регуляторов. Расчет коэффициентов передаточных функций регуляторов для системы с подчиненным управлением осуществляется по методике, приведенной в [9]. Функциональная схема СУ для системы с подчиненным управлением представлена на рис. 2, где W _Пт( р ) - передаточная функция регулятора потокосцепления; W _С( р ) - передаточная функция регулятора скорости; U y ₁ x - управляющее воздействие на выходе канала управления потокосцеплением; U y ₁ y - управляющее воздействие на выходе канала управления скорости; i x - проекция тока статора на ось x ; i y - проекция тока статора на ось у .

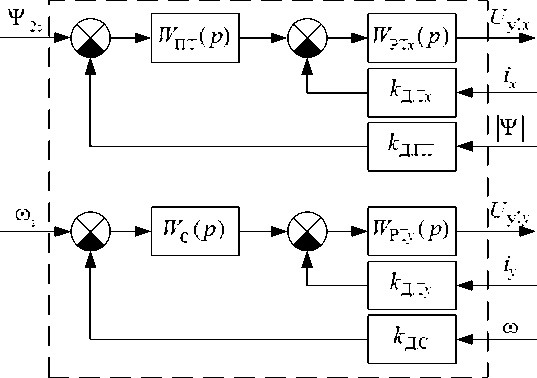
Рис. 2. Функциональная схема СУ системы с подчиненным управлением

Передаточная функция разомкнутого контура тока статора по оси x будет иметь вид

Передаточная функция разомкнутого контура скорости:

W lx ( p ) - W pt x ( p )

k п ^k Д.Т x R э ( t₃ p + 1)

W _m ( p ) - W pc ( p )

^{3 p} п ^k 2 ^г 2 ^k Д.С Jp ( Т _цю p ₊ 1) k ДТу

где W _{pt x}(p ) - передаточная функция регулятора тока; k д.т _x = 1 Ом - коэффициент обратной связи по току i_x .

Так как объект управления представляет собой апериодическое звено, то настройку канала регулирования i_x на модульный оптимум можно обеспечить, используя пропорционально-интегральный (ПИ) регулятор с передаточной функцией:

где Т цш - некомпенсируемая постоянная времени контура регулирования скорости; k д._т y = 1 Ом - коэффициент обратной связи по току i y ; k д._с = 1 В•с/рад -коэффициент обратной связи по скорости.

Для реализации регулятора скорости используется ПИ-регулятор с коэффициентом передачи

W р ( p ) -

Р р ^(тр p + 1) ^ p ’

^k Д.т y^J

3 p п k 2 Г 2 Т k д.с

где Рр - динамический коэффициент регулятора; тр -постоянная времени интегрирующей части регулятора.

Применительно к контуру тока i_x параметры ПИ регулятора имеют вид

P pt x ^-

R э Т э 2 Т _Ц k п k Д.Т x

^{; Т}РТ x ^{- Т}э .

Аналогично выполняется расчет для контура тока по оси у .

Передаточная функция разомкнутого контура потокосцепления:

Определение коэффициентов модального регулятора выполняется методом стандартных уравнений в нормированной форме [8]. Функциональная схема СУ для системы с модальным управлением представлена на рис. 3.

Матрицы динамики и входа разбиты на две пары для синтеза модальных регуляторов по каждому из каналов регулирования [15].

Матрицы канала регулирования потокосцепления

ротора равны

Г 1

—

k 2   )

W г ( p ) - W pпт ( p )

______ ^Т 2 R 2 ^k 2 ^k Д.ПТ ______ Т p + 1)( Т _ц г p + 1) k Д.Т x

A - 1 a ¹¹

^A1 - 1

У a 21

a 12

a 22

T

э

R ₂ k ₂

Т R э Т э

—

T 2

,

где W _РПТ( p ) - передаточная функция регулятора потокосцепления; Т _цР = 2 Т _ц - некомпенсируемая постоянная времени контура потокосцепления ротора; k д. _ПТ = = 1 В/Вб - коэффициент обратной связи по потокосцеплению ротора.

Для реализации ПИ-регулятора потокосцепления используются следующие параметры:

R „ =    k ^Д.^Т x T ² • _{т Т}

Р рпт ~     т. _т ; ^с рпт ^{- Т}2 ,

2 LmkД.ПТ ТцГ где Lm - индуктивность намагничивания.

и матрицы ротора АД:

A2 -

B1 -

b 11

b 21

Г k п

RT

,

канала регулирования скорости вращения

—

—

т

^k 2 p п _Г R э Т э

2 и 0

3p п ^k 2 _Г

У 2 J     ² u ⁰

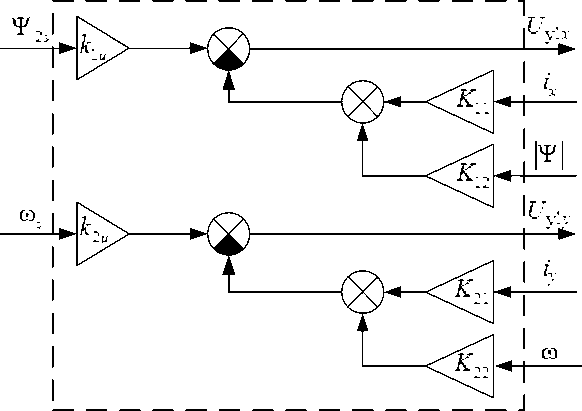
Рис. 3. Функциональная схема СУ системы с модальным управлением

и

B 2 -

Г )

RT

.

Методика расчета коэффициентов модального регулятора ( K ₁₁; K ₁₂) и ( K ₂₁; K 22 ) для обоих каналов регулирования приведена в [17; 18]. Общий вид вектора коэффициентов модального регулятора для обоих каналов регулирования:

a ii ⁺ a 22 ⁺ C о

( K11 L           bii k K12 J    a22 + Ci ' a22 + C0 + a12 ' a21

k              a21 ' bii              j где C0, C1 - коэффициенты типовых нормированных уравнений [8].

Моделирование переходных процессов в среде MATLAB. На рис. 4 изображена структурная схема конденсатного насоса.

Статический момент, создаваемый конденсатным насосом, зависит от частоты вращения ротора машины и в общем виде описывается следующим уравнением:

M _с = M _с о + ( M _сн

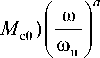
где M _с0 - момент, обусловленный силами трения в механизме; M _:н - статический момент при номинальной скорости ю_н; а - коэффициент пропорциональности (в данном случае а = 2).

Перекачивание жидкости конденсатным насосом представляет собой сложный динамический процесс, включающий гидромеханические процессы в насосе и гидродинамические явления в трубопроводе. При рассмотрении его математического описания используются следующие допущения:

• -    параметры насоса имеют постоянные значения;

• -    режимы теплообмена - установившиеся;

• -    насос перекачивает несжимаемую невязкую жидкость;

• -    течение рабочей жидкости через насос изменяется в соответствии с линейным законом гидродинамики.

При моделировании переходных процессов были выделены два этапа:

• -    первый этап - формирование заданного значения |т₂|;

• -    второй этап - разгон двигателя с воздействием статической нагрузки.

На рис. 5 представлены графики изменения выходных координат системы электропривода с подчиненным управлением: модуля вектора потокосцепления ротора |т₂|, скорости вращения ротора ю и электромагнитного момента M совместно со статическим моментом M _с .

На графиках видно, что при выбранном значении некомпенсируемой постоянной времени T _л = 3,5 мс время переходного процесса подсистемы стабилизации |т₂| равно t _пп^₂ = 42,2 мс, а подсистемы регулирования ю t _ппю = 44,1 мс. Отличие длительности переходных процессов в большую сторону в сравнении с заданными настройками объясняется наличием в каждом канале регулирования вложенного токового контура.

Электромагнитный момент двигателя при разгоне до установившейся скорости превышает статический, что обеспечивает требуемый темп разгона электропривода. Угловая скорость привода достигает всего 69 % от заданной. Повышенное значение статической ошибки регулирования скорости электродвигателя характерна для электропривода с «мягкой» механической характеристикой. В случае насосов, имеющих вентиляторную нагрузку, где момент статический представляет собой квадратичную зависимость от угловой скорости привода, незначительное изменение сопротивления транспортируемой жидкости вызовет значительные изменения скорости и повышенную колебательность переходного процесса замкнутой системы.

На рис. 6 представлены графики переходных процессов в замкнутой системе асинхронного электропривода с модальным управлением . Из графиков видно, что время переходного процесса подсистемы стабилизации |т₂| равно t _пп^₂ = 15,2 мс, а подсистемы регулирования ю t _ппю = 16,7 мс, что достаточно близко к заданным настройкам в выражениях (1) и (2). В установившемся режиме работы угловая скорость привода составляет 87 % от заданной, что значительно выше, чем в случае с подчиненным управлением. В канале стабилизации потокосцепления ротора наблюдается меньшее значение перерегулирования.

Согласно теоретическим исследованиям модальный регулятор позволяет построить грубую систему электропривода. Для исследования обоих систем управления на грубость в модели электропривода было увеличено сопротивление ротора двигателя R ₂ в двадцать раз.

На рис. 7 представлены результаты моделирования. Слева - переходные процессы системы с подчиненным управлением, справа - с модальными регуляторами. Отчетливо видно, что первая система неустойчива, в то время как вторая остается устойчивой и успешно отрабатывает заданные уставки по обоим каналам, изменение сопротивления привело лишь более длительному и колебательному переходному процессу по потокосцеплению.

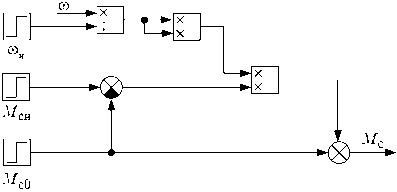
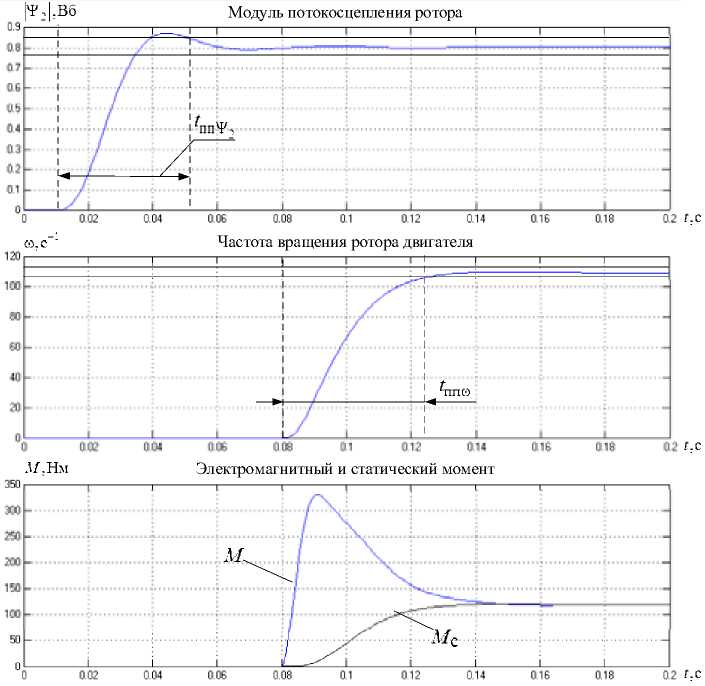
Рис. 5. Графики переходных процессов

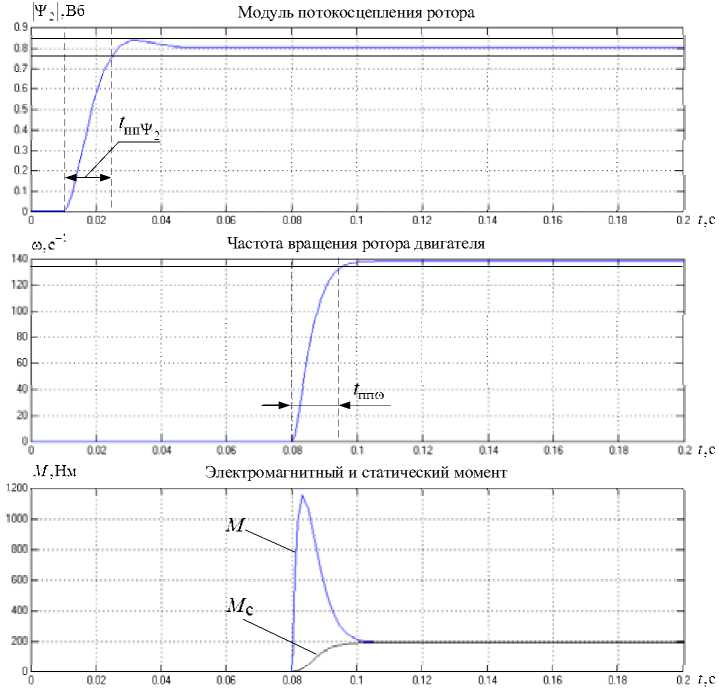
Рис. 6. Графики переходных процессов

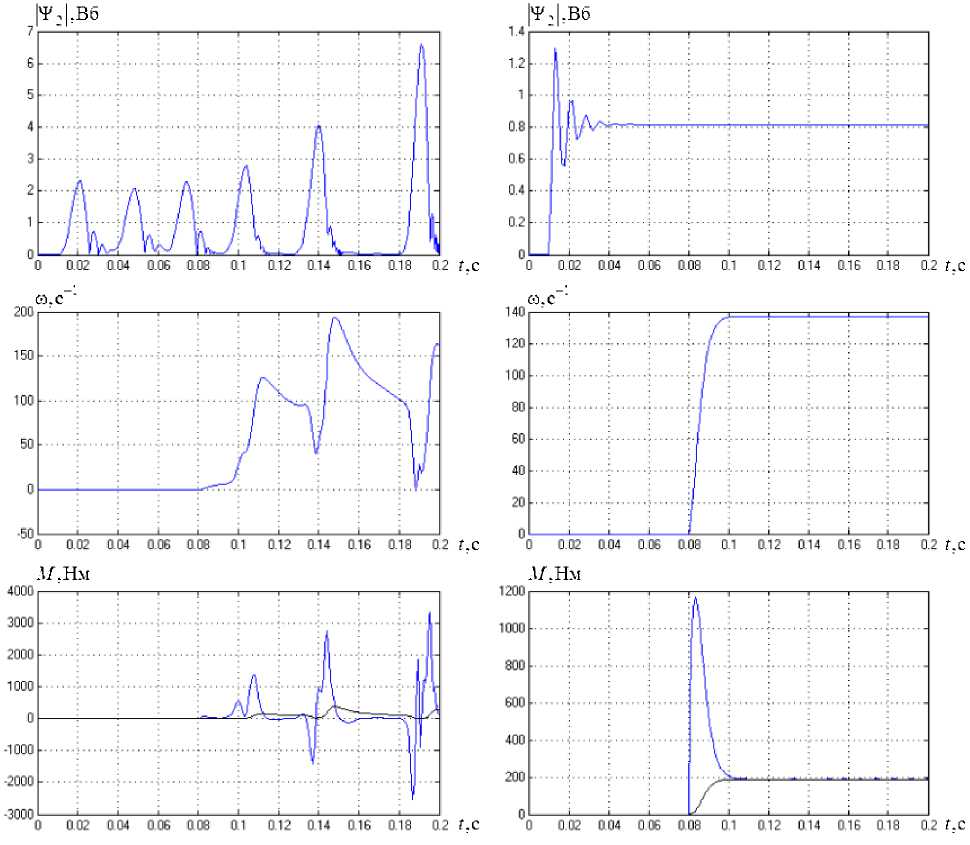
Рис. 7. Графики переходных процессов

Заключение. Сравнивая переходные процессы обоих систем, можно отметить, что в случае с модальным управлением:

• -    обеспечивается более точное соответствие параметров переходных процессов заданным настройкам;

• -    достигается большая жесткость механической характеристики замкнутой системы электропривода.

Имитационное моделирование подтвердило, что модальные регуляторы обладают большей помехоустойчивостью и в меньшей степени зависят от изменения внутренних параметров электродвигателя, чем регуляторы, построенные по принципу подчиненного регулирования.

Последнее имеет большую практическую ценность в промышленности. Использование модальных регуляторов частично снимет необходимость подстройки параметров систем регулирования, что связано со старением оборудования, в результате которого параметры объекта управления претерпевают изменения.

При выходе из строя электродвигателя и отсутствии для замены оригинального запасного в системе электропривода с модальным управлением возможно использование электродвигателя с близкими паспортными данными.