Сравнительная оценка подходов при учёте мощностей
Автор: Грамм Михаил Израильевич
Журнал: Вестник Южно-Уральского государственного университета. Серия: Энергетика @vestnik-susu-power
Рубрика: Краткие сообщения
Статья в выпуске: 37 (296), 2012 года.
Бесплатный доступ
Обсуждаются пределы корректного применения множителей типа комплексных проводимостей и сопротивлений в расчётах мощностей. Показано, что использующий их подход Будеану точен лишь в состояниях, при которых замена ими матрицы системы уравнений состояния корректна. Корректности соответствует совпадение токов с собственными векторами матриц состояния. Более универсален подход Фризе, который в современных условиях цифровой формы измерительной информации прост в реализации.
Электрическая цепь, передаваемая мощность, энергоучёт, собственные векторы, собственные числа
Короткий адрес: https://sciup.org/147158175
IDR: 147158175 | УДК: 62-523.2
Текст краткого сообщения Сравнительная оценка подходов при учёте мощностей
Без ущерба для общности дальнейшего обсуждения рассмотрим простейшую аппроксимацию дифференциального уравнения для RL цепи (рис. 1)
Ldi^ + Ri ( t ) = u ( t ) dt
в форме конечно-разностной схемы расчёта простейшего вида:
■ ( к +1) ■( к -1)
L ( i-------- ----) + Ri ( k ) = u ( к A t ), (2)
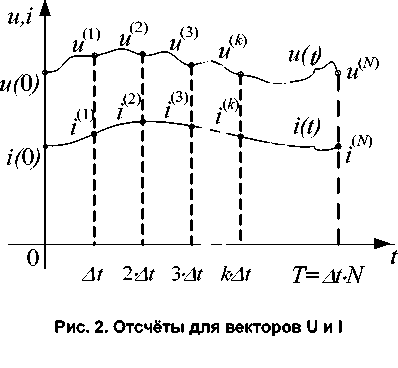
2A t где k=0,1,2,^, N - номера отсчётов массива мгновенных значений (ММЗ) с шагом At< Рис. 1. Двухполюсник RL Введём условие периодичности i(0)=i(N и обозначение b = (L /2)-At: Краткие сообщения ■ i(1) " R b 0 ... -b u (At) -b R b ... 0 i (2) u (2 -At) 0 -b R ... 0 i (3) = u (3 -At) ............... i (k) u (k -At) b 0 0 - b R u (N -At) i (N) Z-I = U. (3) При расчётах по Будеану матрица Z в (3) заменяется комплексным множителем. С его помощью рассчитываются мощности: активная, реактивная, искажения и т. п. [1–6]. С алгебраической точки зрения ясно, что замена Z множителем корректна лишь в случае, когда вектор I является собственным вектором матрицы Z. Собственными векторами циркулянта Z являются синусоиды [1, 7]. В ином подходе – по С. Фризе проблема принадлежности I и U к собственным векторам матрицы Z несущественна. Постулируется физически прозрачный факт - к произвольному моменту t=k-Δt цепью потреблена лишь энергия, определяемая коллинеарной вектору U(k) составляющей Ir(k)тока I(k). Известная [1] процедура проектирования одного вектора на заданный другой даёт эту составляющую: I (k) = (U(k),I(k)) - U(k) = g(k) U(k), (4) r (U(k), U(k)) где g(k) – текущая скалярная проводимость цепи к моменту t = k At. За время t = k At энергия, связанная с коллинеарной компонентой, составит величину Wr(k)= = [Ir(k),U(k)]- At, а её учёт после деления на число отсчётов за весь период отсчёта-наблюдения Tнаб даст величину активной мощности по Фризе: P=[Ir(N),U(N)]/N=(I, U)/N. (5) Величина (5) окажется равной P=UI-cos( фk ) лишь для синусоиды с амплитудой UmK и целым числом K периодов UkK) = UmK-sin(2 пkK/N+фk), укладывающихся в отрезок наблюдения k=0,1, 2,… N (начальная фаза синусоиды тока К-й гармоники считается нулевой). В практическом энергоучёте различие результатов, получаемых в подходах по Будеану и по Фризе, как правило, игнорируется. Объясняется это преобладанием промышленной и более высоких частот в напряжениях и токах сложной формы. Положение может быстро измениться из-за появления множества источников альтернативной энергии и соответствующего усложнения сети длинных линий. В [8] обращено внимание на существование в сложных схемах с запаздываниями процессов, существенно превышающих по длительности рабочие отрезки Tнаб стандартных счётчиков энергии. В результате конфликты между показаниями систем энергоучёта на входе в систему и показаниями на нагрузках с усложнением схем могут стать серьёзной проблемой. Дело не только в том, что для низкочастотной синусоиды условия периодичности могут оказываться не выполненными для конкретного счётчика. В дело вступает физика процессов. Величина энергии, полученная с помощью (5) для произвольного t = k At на входе линии, может оказаться далёкой от величины, действительно необратимо использованной цепью на выходе к моменту t. В линиях колеблется собственный запас энергии, и учитываемая на входе «коллинеарная энергия» к любому моменту t от начала отсчёта, равная сумме интеграла от мощности потерь и энергии, запасённой к моменту t в реактивностях линии и нагрузки за вычетом начального запаса Wq(0) в них. Например, для обсуждаемой RL-цепи непрерывное описание «коллинеарной энергии» достаточно очевидно: Wr (t) = L^ + J Ri (t )2 dt — L2^)2 .(6) Дискретной проводимости g (k) в (4) соответствует плавная функция проводимости: tt g(t) = J u (t) - i(t) - dt / J u (t)2 - dt.(7) Числитель в (7) даёт величину введённой в цепь к моменту t энергии (включая энергию, затраченную на накопления в реактивностях линий и цепей, в обратимых аккумуляторах и т. п., то есть «невозвращённую» на вход в любом виде). Её вычисление возможно с помощью функции g (t): t Wr (t) = g(t) J u(t)2dt. (8) Именно расчёту по (8) и соответствует операция Wr(k) =g(k)-[U(k),U(k)] At. Её целесообразно выполнять и для входа, и для выхода. Отчасти этим и объясняется появление активной мощности, потребляемой линией без потерь. Возникают весьма нетрадиционные проблемы КПД линии без потерь, компенсации реактивной мощности линии и др. [8]. Описанная «коллинеарная энергия» Wr (k), будучи энергией принятой цепью в том или ином виде, принципиально отличается от «неактивной» или «реактивной» энергии Wx (k), не принятой к моменту t = k At. Она пропорциональна ортогональной на отрезке 0–t к функции внешнего воздействия составляющей состояния. Например, именно взаимная ортогональность на отрезке в период делает гармоники Фурье энергетически независимыми. В ортогонализации разницы «параметр состояния - воздействие» состоит также и суть методов типа Ритца, Бубнова–Галёркина и подобных им [1]. В электрофизике на это впервые обратил внимание О. Хевисайд, заметив, что в Грамм М.И. Сравнительная оценка подходов при учёте мощностей теореме Дж.Г. Пойнтинга учёт передаваемой мощности требует расчёта не потока вектора Пойнтинга, а дивергенции этого вектора. Тогда вихревая составляющая вектора Пойнтинга выпадает, поскольку дивергенция ротора тождественно равна нулю. Энергию передаёт только потенциальная составляющая, которая и описывается вектором I r (к). Не углубляясь в теорему Стокса и в расположения составляющих вектора Пойнтинга вокруг фидера передачи энергии, кратко опишем количественную оценку «неактивной энергии». Здесь обнаруживается дополнительное удобство введения по Фризе коллинеарной составляющей тока. Оно состоит в простоте определения другой составляющей - ортогональной Ix (к), которая должна удовлетворять условию ортогональности (U(к), Ix (к)) = 0. Она равна разнице Ix (к ) = I (к) -1r (к). Составляющая Ix (к) на отрезке времени 0 - к At даст условную величину «неактивной энергии» Wx (к) = |Ix (к)|- |и (к)|-At, которая при k=N для синусоиды с целым числом К периодов в Tнаб в точности равна величине традиционной реактивной мощности Q (T) = = Wx (Тнаб)/N At, позволяющей проверить величину и часто вычисляемой реактивной проводимости b(T). Ортогональность векторов Ix (к) и U (к) обеспечивает выполнение «правила треугольника» для векторов Ix(к), Ir (к) и I (к). Оно верно и для комплекта Wr (к) = (Ir (к), U(к))-At, Wx (к ) = [| Ix (к )|- |U (к )| J -At и условной «полной энергии» W(к) = |I(к)|-|U(к)|-At при любой форме i (t) и u (t) и для любого момента t. Также возникает возможность непрерывного отслеживаНИя угла ф(к)= arctg [|Ix (к)|/IIr (к)|] между накопленными к моменту к At векторами U (к) и I (к). Возникает алгоритм непрерывного мониторинга качества поставляемой и потребляемой энергий. В варианте подхода с использованием коллинеарной составляющей нет места «мощностям искажения» и т.п. искусственным прибавкам. Применяемые в нём расчётные формулы и вытекающие из них алгоритмы учёта не зависят от форм u (t) и i (t), а также их точность не зависит от величины периода отсчётов Tнаб. Алгоритмы весьма просто могут быть реализованы стандартными процедурами блоков линейной алгебры.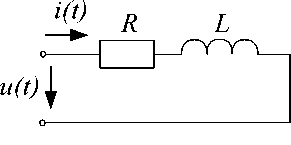
Список литературы Сравнительная оценка подходов при учёте мощностей
- Грамм, М.И. Матрично-спектральные методы расчётов в электротехнике и принцип минимума потерь/М.И. Грамм, Ю.Н. Немов, Ф.Н. Шакирзянов. -М.: Изд. Дом МЭИ, 2006.
- ГОСТ Р 52425-2005. Аппаратура для измерения электрической энергии переменного тока. Частные требования. Часть 23. Статические счетчики реактивной энергии.
- Hirofumi, Akagis. Instantaneous power theory and applications to power conditioning/Akagi Hirofumi, Edson Hirokazu Watanabe, Mauricio Aredes. -N.Y., Tokyo.: John Wiley and Sons, 2007.
- Fryze, S. Wirk-, Blind-und Scheinleistug in elektrischen Stromkreisen mit nichtsinusformigem Verlauf von Strom und Spannung/S. Fryze. -Elektrotechnische Zeitschrift, 1932. -Heft 25.
- Budeanu, C.I. Puisslanses reactiv’es et fictives/C.I. Budeanu. Inst. Romain de I’Energie. -Bucharest, Rumania, 1927.
- Розанов, Ю.К. О мощностях в цепях переменного и постоянного токов/Ю.К. Розанов//Электричество. -2009. -№ 4.
- Грамм М.И. О прикладных следствиях одной математической традиции//Вестник ЮУрГУ. «Энергетика». -2001. -Вып. 1. -№ 4.
- Волновые явления в неоднородных структурах/В.К. Римский, В.П. Берзан, В.И. Пацюк и др. -Кишинев, 2009. -Т. 5.


