Сравнительная оценка результатов численного моделирования гидродинамических процессов в системе "ванна с расплавом - МГД-перемешиватель"

В процессе приготовления многокомпонентных сплавов важной технологической операцией является перемешивание расплава с целью выравнивания химического состава и температуры во всем объеме ванны миксера. Для этих целей применяют магнитогидродинамические (МГД) перемешиватели. По принципу действия МГД-перемешиватели представляют собой линейную индукционную машину (ЛИМ). Но по сравнению с ними имеется большой немагнитный зазор между индуктором и металлическим расплавом, достигающий величины τ/π и более [1]. Основным достоинством электромагнитного перемешивания является отсутствие контакта с высокотемпературным и агрессивным расплавом и возможность автоматизировать операцию перемешивания. МГД-перемешиватели могут размещаться по отношению к металлу под днищем ванны (поворотные миксера) или сбоку (стационарные миксера). Использование МГД-перемешивателей жидких металлов в печах и миксерах при производстве металлических сплавов постоянно растёт. В настоящее время почти все печи-миксеры в плавильно-литейном производстве алюминиевых сплавов оснащаются МГД-перемешивателями.

Проектирование МГД-перемешивателя основано на выполнении сопряженных электромагнитных и гидродинамических процессов, а именно на определении энергетических и геометрических параметров индуктора, а также его расположении относительно расплава. Математическое моделирование таких систем выполняется аналитическими и численными методами и представлено в работах [2–4]. Как правило, моделирование гидродинамической стороны этих задач выполняется численными методами в связи с турбулентным характером процессов. В свою очередь, моделирование турбулентности с учетом реальных возможностей вычислительной техники основано на использовании полуэмпирических моделей, среди которых модели типа RANS, основанные на осреднении турбулентности, и модели типа LES, основанные на явном моделировании турбулентных пульсаций крупных вихрей. Наиболее известны и широко применяемы RANS-модели k-ε, k-ω, SST.

Модель турбулентности k-ε является двухпараметрической, в которой решаются два дополнительных уравнения для расчета кинетической энергии турбулентности k и скорости диссипации кинетической энергии ε. Для расчета скорости у стенки используют пристеночные функции. Данная модель турбулентности получила широкое применение в решении практических инженерных задач. Она хорошо подходит для решения задач внешнего обтекания тел.

Модель k-ω похожа на k-ε, в которой решается уравнение удельной скорости диссипации кинетической энергии ω. Также эта модель может быть использована совместно с пристеночными функциями. Хорошо подходит для решения задач, где требуется моделирование внутренних течений, отрывных и струйных течений.

Модель SST является разновидностью k-ω, которая совмещает две модели турбулентности – k-ω и k-ε. Для расчета течений в пристеночных областях используют модель k-ω, а на удалении от стенки – модель k-ε. Данную модель применяют для широкого класса течений, так как сочетание моделей делает её более точной и надежной [5].

Метод моделирования LES использует систему «фильтрующих» уравнений. Эти уравнения исключают из явного расчета подсеточные вихри, которые по размеру меньше, чем ячейки расчетной сетки. Эту модель обычно применяют в задачах с простыми геометрическими областями из-за высокого требования к вычислительным ресурсам [6].

Таким образом, для сравнительной оценки качества моделирования гидродинамических процессов в алюминиевом расплаве в ванне печи-миксера актуально выполнить численные расчеты с различными моделями турбулентности и провести их анализ. Как известно, те или иные модели турбулентности чувствительны к плотности расчетной сетки, особенно в слое пристеночного течения, характеризуемого безразмерным параметром Y+. В связи с этим сравнительные расчеты актуально выполнить при различном размере расчетных элементов сетки.

Для численного расчета гидродинамических процессов широкое применение получил метод конечных объемов (МКО). На его основе создано множество программных комплексов, среди которых наиболее популярны StarCD, OpenFOAM, Fluent и CFX.

Математическая модель

Эскиз системы «ванна с расплавом - МГД-перемешиватель» представлен на рис. 1 и состоит из ванны с расплавом 1 и МГД-перемешивателя 2. Гидродинамический расчет выполняется в области расплава 1 с заданием требуемых граничных и начальных условий. Влияние электромагнитного поля учитывается введением в уравнения движения соответствующего источникового члена, полученного аналитическим или численным методом при выполнении электромагнитного расчета.

Предварительная оценка характера гидродинамических процессов, протекающих в жидком металле, выполняется через критерий подобия течения вязкой жидкости. Число Рейнольдса характеризует отношение инерционных сил к вязким и позволяет оценить турбулентность течения:

Re = Р"v'Dr , (1) µ где ρ – плотность, ν – характерная скорость, DГ – гидравлический диаметр, μ – динамическая вязкость.

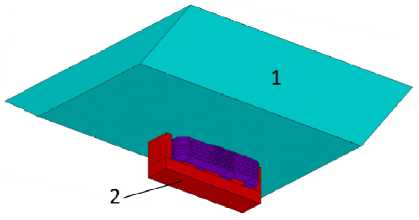
Рис. 1. Эскиз системы

Fig. 1. System sketch

Система уравнений, описывающая гидродинамические процессы, состоит из уравнений сохранения массы (2) и движения (3):

∂ρ+∇(ρ⋅v)=s ∂t

∂ρ ⋅ v+ V( p-v • v) = -Vp— Vt + p-g + sr,                            (3)

∂t где sp, sv - источниковые члены уравнений сохранения массы и движения; p - давление; т - тензор вязких напряжений.

В данной системе для оценочных расчетов можно считать, что температурное поле в расплаве однородно и естественные конвективные течения отсутствуют, а сам расплав несжимаем. Таким образом, ρ(x, y,z,t)=CONST=ρ 0 , следовательно, ∂ρ/∂t= 0, а членом уравнения ρ·g можно пренебречь. В качестве источниковых членов уравнений движения при решении задач магнитной гидродинамики служит сила Лоренца f эм . С учетом вышесказанного система уравнений (2–3) принимает вид

Vv=0,                                                                 (4)

^{∂ ρ} 0 ^{⋅ v} +∇ ( ρ 0 ⋅ v ⋅ v ) =-∇ p +∇ τ + f ЭМ .                                 (5)

∂ t

Для данной задачи число Рейнольдса составляет 540 5 - 20 ^ 10 5 , что говорит о сильно турбулентном течении. Соответственно, очевидна необходимость использования моделей турбулентностей. Модели турбулентности основаны на решении дополнительных уравнений для нахождения рейнольдсовой составляющей тензора вязких напряжений уравнения движения (5). Вид дополнительных уравнений определяется выбранной моделью турбулентности и представлен в [7].

Анализ результатов

В задаче рассмотрены три сетки с различными размерами элементов (рис. 2). Общее количество элементов расчетной сетки для трех случаев составило: 82500 (а) – детализированная, 14000 (б) – базовая и 3230 (в) – грубая. Шаг по времени для соблюдения чистоты численного эксперимента принят одинаковым во всех случаях и определен из условия Куранта для минимального размера элементов. На границах расчетной области задано условие стенки с прилипанием. Время расчета задачи составило по методу RANS в среднем: для детализированной сетки 240 мин, для базовой сетки 38 мин и для грубой сетки 18 мин; по методу LES время составило: 420, 62 и 22 мин, соответственно.

С помощью представленной выше математической модели была выполнена группа расчетов с использованием моделей турбулентности k-ε, k-ω, SST и LES. Полученные в результате расчетов поля скоростей в конечный момент времени для всех случаев изображены на рис. 3. Для LES-модели показана осредненная составляющая поля скоростей.

По полученным результатам видно, что во всех случаях возникает два контура. В k-ε и LES структура течений не изменяется при переходе на более детализированную сетку. В моделях k-ю и SST заметна чувствительность результирующего поля скоростей к разме- – 141 –

а)                            б)                           в)

Рис. 2. Средний размер элементов сетки в области расплава: 5 см (а); 10 см (б); 15 см (в)

Fig. 2. Average size of mesh elements in the melt area: 5 cm (a); 10 cm (б); 15 cm (в)

детализированная            средняя                 грубая

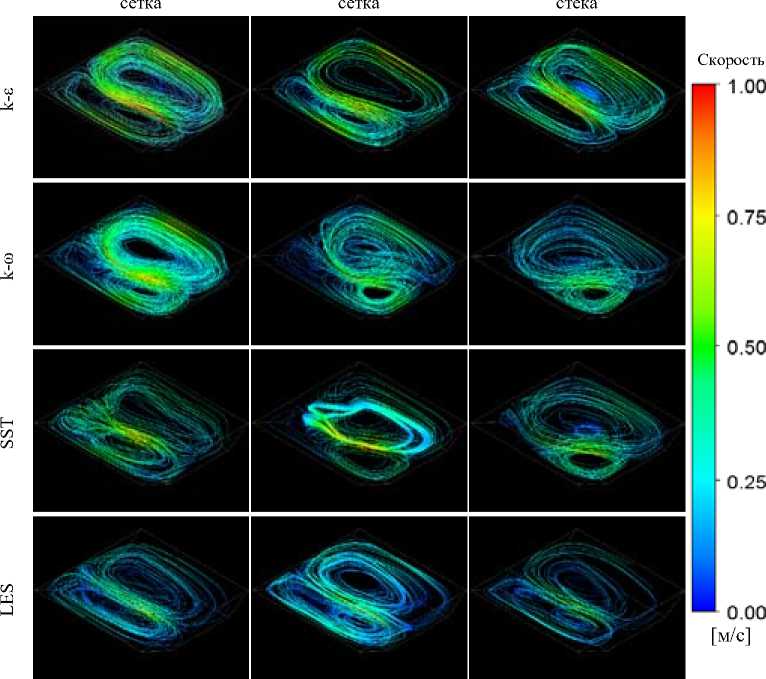
Рис. 3. Траектории течений

Fig. 3. Flow trajectories ру расчетной сетки, при загрубении сетки меняется размер и положение формирующихся вихрей.

Для оценки качества расчетов рационально изучить распределение и величину параметра Y+, который зависит от размера элементов в пристеночной области и скорости в них. На рис. 4 – 142 –

а)

б)

в)

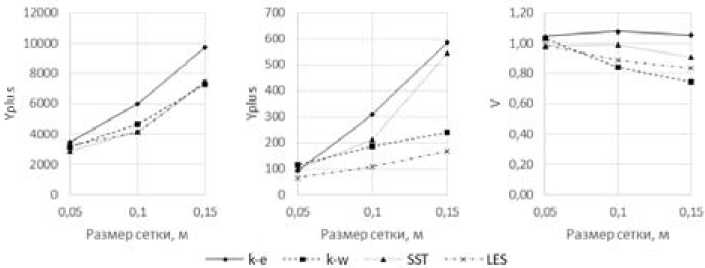
Рис. 4. Графики зависимости максимальной Y+ (а), минимальной Y+ (б) и максимальной скорости (в) от размера сетки

Fig. 4. Graphs of maximum Y + (a), minimum Y + (б) and maximum speed (в) from the grid size

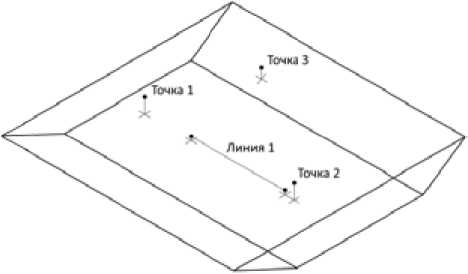
Рис. 5. Линии и точки для исследования величин скоростей

Fig. 5. Lines and points for the study of speed values представлены полученные для данных задач максимальные по объему скорости и соответствующие значения параметра Y+.

Так как течение в рассматриваемой области относится к высокорейнольдсовым, значения Y+ (рис. 4 а,б ) получились большими. В большинстве случаев CFD решений пристеночные функции работают непредсказуемо при Y+<30, таким образом, в нашем случае Y+ является приемлемым [8]. Как видно на рис. 4 в , максимальная скорость для модели турбулентности k-ε не меняется при изменении размера сетки, а для других моделей уточняется и стремится к одному значению скорости.

Для анализа полученных результатов моделирования течений в расплаве при разных моделях турбулентности и различной детализации сетки были построены графики скоростей на определенных участках внутри расплава относительно МГД-перемешивателя (рис. 5).

На рис. 6 представлены графики зависимости средней скорости на линии 1 от времени, характеризующие режим работы индуктора.

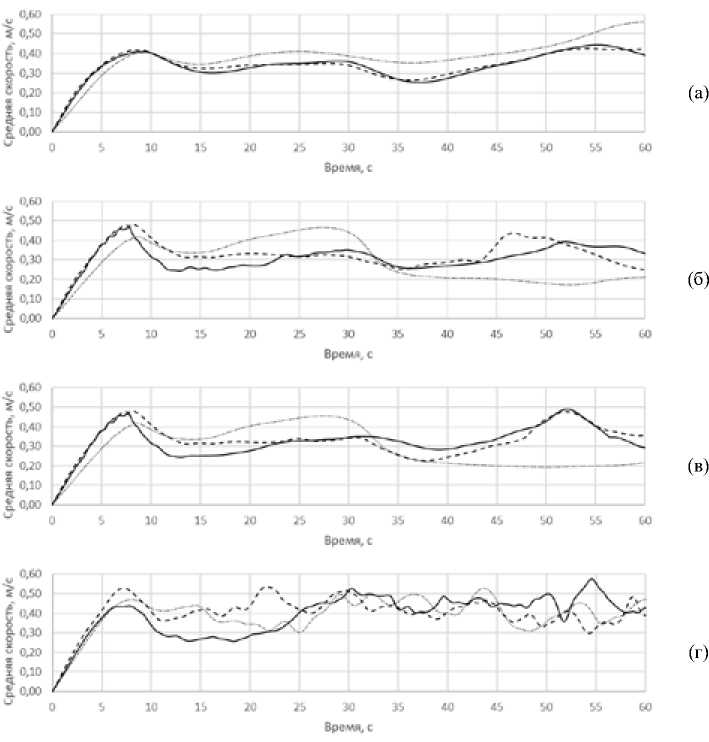
Детализированная ----Базовая --------Грубая сетка

Рис. 6. Графики средней скорости на линии 1 от времени: а – k-ε; б – k-ω; в – SST; г – LES

Fig. 6. Graphs of the average speed versus time on line 1: a – k-ε; б – k-ω; в – SST; г – LES

Как видно из графиков, динамика течений во всех случаях схожа и находится в определенном диапазоне значений скорости. Первые 7-8 с соответствуют ламинарному участку ускорения потока от нулевого значения. В интервале 10-25 с течение замыкается и переходит в турбулентное. Для LES-модели показаны графики с учетом внутрисеточных пульсаций.

Для количественной оценки чувствительности расчета детализации расчетной сетки всех моделей турбулентности была найдена средняя скорость в трех характерных точках течения (рис. 4) и её максимальное отклонение (разброс) при загрублении сетки. Полученные результаты сведены в табл. 1.

Из-за низкочастотных колебаний гидродинамических потоков во времени такая оценка оказалось достаточно грубой, однако позволила оценить чувствительность расчетов к сетке и провести количественное сравнение всех моделей. Так, в среднем чувствительность составила: 11 % для k-ε, 14 % для k-ω, 15 % для SST и 8 % для LES. Отклонение величины скорости по – 144 –

Таблица 1. Средняя скорость в трех характерных точках течения

Table 1. Average velocity in three characteristic points of the flow

Модели турбулентности Точка 1, v [м/с] (разброс [%]) Точка 2, v [м/с] (разброс [%]) Точка 3, v [м/с] (разброс [%]) k-ε 0,334 (16,2) 0,357 (9,4) 0,441 (6,3) k-ω 0,280 (10,7) 0,351 (9,0) 0,335 (21,0) SST 0,278 (19,4) 0,369 (11,3) 0,359 (14,2) LES 0,333 (13,6) 0,336 (2,2) 0,355 (7,2) абсолютному значению в зависимости от типа моделей турбулентности в различных точках равно от 0,03 до 0,1 м/с, что относительно некоторого среднего значения составляет от 10 до 30 %.

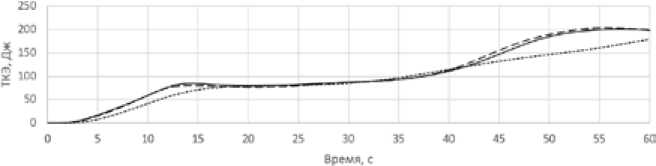
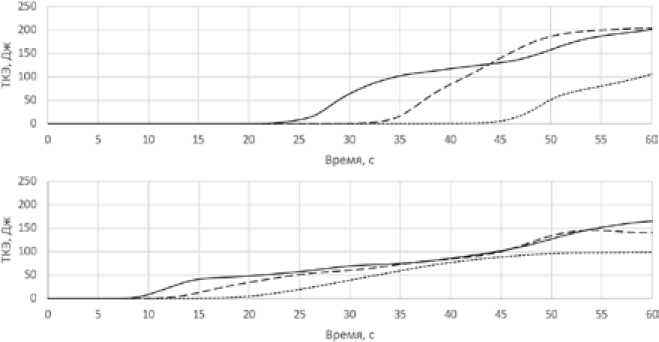
Так как RANS-модели основаны на расчете распределения осредненной скорости с определением зависимых вспомогательных турбулентных характеристик, необходимо оценить поведение дополнительных параметров модели. Одним из таких общих параметров для всех моделей является турбулентная кинетическая энергия. От корректности определения данной величины зависят турбулентные составляющие эффективной вязкости и, при решении сопряженной задачи термодинамики, эффективной теплопроводности. Динамика интегрального по объему значения турбулентной кинетической энергии (ТКЭ) представлена на рис. 7.

Характер изменения ТКЭ для всех RANS-моделей получился различным. Однако для моделей k-ω наблюдается максимальная задержка её возникновения и, вместе с тем, значительная чувствительность к детализации сетки.

Заключение

В данной статье представлена сравнительная оценка результатов численного моделирования гидродинамических процессов в МГД-системе при различных моделях турбулентности и детализациях сетки. Проведено взаимное сравнение результатов по основным гидродинамическим характеристикам, а именно осредненной и мгновенной скорости, турбулентной кинетической энергии, а также проведена оценка вспомогательного параметра Y+.

Установлено, что при увеличении размера элементов расчетной сетки средняя скорость в объеме расплава имеет тенденцию к снижению, что вызвано загрублением аппроксимации пограничного слоя, характеризуемой параметром Y+. Однако модель k-ε оказалось наименее чувствительна к размеру сетки и дает наиболее стабильные результаты как по характеру поля скоростей, так и по его величине. ТКЭ также для k-e не зависит от сетки. Модель LES по основным осредненным параметрам дает достаточно близкие к k-e результаты, однако более требовательна к вычислительным ресурсам. Основным достоинством LES является возможность изучения пульсирующей составляющей поля скоростей. Наименее стабильные результаты по- – 145 –

(а)

(б)

(в)

Детализированная ---- Базовая ........— Грубаясетка

Рис. 7. Турбулентная кинетическая энергия (ТКЭ) моделей турбулентности от времени: а – k-ε; б – k-ω; в – SST

Fig. 7. Turbulent kinetic energy (TKE) turbulence models from time: a – k-ε; б – k-ω; в – SST казала модель k-ω и, соответственно, SST-модель, являющаяся совмещением k-ε и k-ω. При детализации сетки до размера элементов до 0,05 м результаты для всех моделей турбулентности становятся идентичными.

Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований, Правительства Красноярского края, Красноярского краевого фонда поддержки научной и научно-технической деятельности в рамках научного проекта №16-48-242018 р_офи_м.