Сравнительная оценка способов питания СДПМ в режиме вентильного двигателя

Синхронные двигатели с постоянными магнитами (СДПМ), работающие в режиме вентильного двигателя (ВД), нашли в последнее время широкое применение в различных отраслях техники [1–5]. Для реализации векторного управлении такими двигателями при питании их от источника трёхфазного синусоидального напряжения наибольшее распространение получил принцип формирования вектора потока статора путём управления токами по ортогональным осям d и q во вращающейся системе координат, связанной с намагниченным ротором [6–9]. За счёт изменения каждой из составляющих результирующего вектора тока ( i d и i q ) удаётся регулировать угол между полями ротора и статора и амплитуду вектора поля статора. Такой подход при расчёте токов требует два преобразования координат – от неподвижной трёхфазной системы к вращающейся двухфазной и после формирования заданных значений токов i_d и i_q , наоборот, – от двухфазной к трёхфазной системе. Как правило, такое преобразование осуществляется стандартными программами и требует дополнительных вычислительных ресурсов и чаще всего импортных стандартных преобразователей [10–12]. Кроме того, эффективность метода существенно снижается при наличии несинусоидальности токов или потокосцеплений.

Между тем, при наличии датчика углового положения ротора двигателя относительно осей статорной обмотки, взяв за начало отсчёта магнитную ось одной из фаз, мы можем непосредственно измерять угол между полями ротора и статора. На практике лучше пользоваться углом между ЭДС вращения и первой гармоникой напряжения двигателя, который связан с углом между векторами полей ротора и статора. Регулируя этот угол путём сдвига по фазе трёхфазного напряжения или тока относительно фазной ЭДС, мы можем изменять вид рабочих характеристик привода [13, 14]. При этом упрощается схема управления, сокращается количество вычислительных процедур и исключаются ошибки, обусловленные неси-нусоидальностью токов и потокосцеплений. Такой метод называют методом фазового векторного управления (ФВУ).

В некоторых приводах весьма эффективным оказывается применение двигателей с дискретной коммутацией фазных обмоток. Эти двигатели называют бесконтактными двигателями постоянного тока (БДПТ) [15, 16]. С точки зрения технической реализации электропривод с дискретной коммутацией фазных обмоток оказывается значительно проще электропривода с позиционной модуляцией фазных напряжений по синусоидальному закону. Это объясняется тем, что управление коммутацией фаз может быть реализовано по простым алгоритмам на простейших микроконтроллерах, а частота ШИМ фазных напряжений при управлении двигателем может быть существенно снижена, так как нет необходимости формирования их по синусоидальному закону. Особенно это важно в электроприводах, где требуется высокая частота напряжения питания электродвигателя. Очевидно, что в таком приводе невозможно реализовать векторное управление с регулированием токов по осям d и q, так как токи и напряжения в них существенно несинусоидальны, но вполне возможна реализация ФВУ.

Постановка задачи исследования

Прежде чем рассматривать вопросы ФВУ, необходимо уточнить, какие из способов дискретной коммутации наиболее эффективны, и оценить, как они соотносятся по виду механических характеристик и энергетических показателей, а также пульсациям электромагнитного момента между собой и со случаем синусоидального напряжения питания. Это позволит обоснованно выбрать тот или иной способ питания СДПМ и способ векторного управления. В настоящей статье предпринята попытка осуществить такую оценку.

Математическое описание статических характеристик электродвигателей

Для математического описания статических характеристик СДПМ с неявно выраженными полюсами при синусоидальном питании воспользуемся известными из классической теории таких машин уравнениями для токов по осям d и q [17]:

_   Um(—rsin6+toZcos6)— nlEm d =         (^1)2+72        ;                      ( )

U m (7COS0+^lsin0)—rE m

‘ q =          ( _M l) 2 +r²          .                         ⁽²⁾

Здесь r – активное сопротивление фазной обмотки; l – индуктивность фазной обмотки с учётом взаи- моиндуктивности с другими фазами; Um, Em – амплитуда напряжения и ЭДС соответственно; m = 1, 2, 3 – номер фазы; θ – угол сдвига между векторами напряжения и ЭДС, ω – скорость вра- щения ротора в электрических координатах.

Электромагнитная мощность двигателя определяется выражением

P ₃=³ " E _m I _q .                                 (3)

Электромагнитный момент определим из со- отношения

М_э=^_- v I_o ,                        (4)

э и 2 Yrn q’ где vm — коэффициент связи между амплитудой фазной ЭДС и частотой вращения ротора.

Потребляемую активную мощность опреде- лим из соотношения

Р _а = U _d I _d + U _q I _q =

=--U. sin9I +-U cos9L . 2 z/t                   2 zzt          q

Подставим токи и после преобразований по- лучим

_D _ 3 U_m(E_m(raisin0—rcos0)+rU_m) а = 2        (й)²^²         .

Под электромагнитным КПД принято пони- мать отношение электромагнитной мощности к потребляемой активной, поэтому его будем счи- тать по выражению

П э = ^ (6)

Для того чтобы сравнивать различные способы питания двигателей, хотелось бы иметь такие же относительно простые выражения для расчёта перечисленных выше величин и для случая дискретной коммутации. Существует несколько способов дискретной коммутации трёхфазной обмотки (СДПМ). Мы рассмотрим наиболее распространённые из них [18].

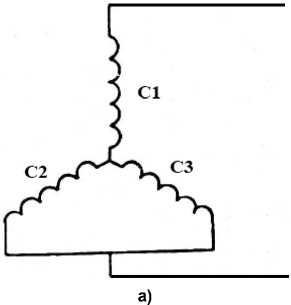
180-градусная шеститактная коммутация, при которой на каждом межкоммутационном интервале (МКИ) к источнику питания через полупроводниковый коммутатор оказываются подключёнными три фазы, как показано на схеме замещения (рис. 1а).

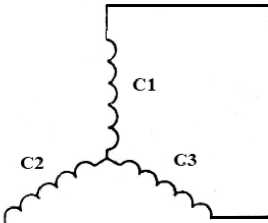
120-градусная шеститактная коммутация, когда на каждом МКИ к источнику питания оказываются подключёнными две фазы (рис. 1b).

150-градусная двенадцатитактная коммутация, представляющая собой сочетание первых двух, когда обмотка двигателя, чередуясь, подключается к источнику постоянного тока по схеме рис. 1а и 1b.

Если пренебречь индуктивностью рассеяния статорной обмотки, то можно получить относи- тельно простые выражения для описания механической (МХ) и энергетической характеристик (ЭХ) [19, 20]. В относительных единицах при нулевом значении угла коммутации (θ = 0) они имеют вид:

– для 180-градусной коммутации

_ y(k i —y) .

^П “ (1—k i V) ;

_Ц^{_ (}k i ^- v);

– для 120-градусной коммутации

_ v(k i —k₂v)

^П “ (1—k i V) ^;

Ц _ (k i - ^ 2 V).

Также по уравнениям (3)–(6) можно

(6а)

(7а)

(6б)

(7б) предста-

вить в относительных единицах электромагнитный КПД и электромагнитный момент для случая си- нусоидального питания двигателя:

П = v;                                      (6в)

ц _ 1 - v.                                (7в)

В уравнениях обозначено v и ц соответственно относительная скорость и относительный электромагнитный момент двигателей при нулевой индуктивности и нулевом угле коммутации, а коэффициенты определяются по выражениям k₁ = 3/п, k₂ = 2 (1 + З^ ³). В качестве базовых величин примем мощность и момент в пусковом режиме ( Р п , М п ), а также скорость, при которой амплитуда ЭДС вращения равна амплитуде напряжения при синусоидальном питании, или ЭДС эквивалентной обмотки (см. рис. 1) равняется напряжению на шинах постоянного тока. В частности, учитывая, что амплитуда выходного напряжения трёхфазного мостового инвертора в лучшем

b)

Рис. 1. Схема подключения фаз СДПМ к источнику постоянного тока: а – при 180-градусной коммутации; b – при 120-градусной коммутации Fig. 1. Wiring diagrams of phases of PMSM to a DC source: a – at 180-degree commutation; b – at 120-degree commutation

Un случае равна иа = ^=, а также принимая во внимание схемы рис. 1, получим:

– для 180-градусной коммутации

Un 3              2 Un мб = V-^ш; Юб = -• —;

2Г 23

– для 120-градусной коммутации мб = U • V3y ; Юб = -тип-;(Б)

б 2г уш’ б Тз^ш

– для синусоидального напряжения

Мб = Т3ип • V3y ; юб = — б 2г      Тш’ б   Тз^ш

– для 150-градусной коммутации аналитические соотношения для зависимостей μ = f ( ν ) и η_э = f ( ν ) выводить не будем, полагая, что они будут находиться между характеристиками 120- и 180-градусной коммутации, что будет показано ниже в результате численных расчётов.

В некоторых случаях к электроприводу предъявляются требования по допустимым пульсациям момента в процессе вращения ротора. Оценивать такие пульсации будем по угловой моментной характеристике двигателя. Сразу можно отметить, что при синусоидальном питании в идеальном случае линейности магнитной системы такие пульсации отсутствуют. Что касается дискретной коммутации, то здесь в течение МКИ момент будет меняться в связи с дискретным характером электромагнитных процессов. При нулевой индуктивности пульсации момента достаточно просто получить аналитически. В частности, согласно [19, 20], для 180-градусной коммутации наличие короткозамкнутого контура даёт дополнительное изменение момента. В результате имеем

Ц = cos (ф - п ) - ^V • cos² (ф - б )-

-^T3sin²(V- ^ )v².                         (8а)

Для 120-градусной коммутации при нулевой индуктивности и при θ = 0 мгновенное относительное значение момента на МКИ можно записать соотношением ц = cos (ф - п) - v • cos2 (ф - п),         (8б)

где φ = ω t – текущее значение угла поворота ротора на МКИ, изменяющееся в интервале от 0 до π/3.

При 150-градусной коммутации характер изменения момента по аналогичным выражениям необходимо оценивать на интервале δ = π/6 для обеих схем рис. 1.

К сожалению, аналогичные наглядные выражения для мощностей и моментов ВД при ненулевой индуктивности могут быть представлены только при синусоидальном питании. Для расчёта мгновенных фазных токов и мощностей в установившемся режиме для дискретной коммутации придётся решать дифференциальные уравнения электромагнитных коммутационных процессов, как это показано, например, в [18], и по ним определять средние интегральные на МКИ значения токов и мощностей.

Для выполнения сравнительного анализа способов питания статора вентильного двигателя с учётом индуктивности статорной обмотки в программе Simulink была составлена вычислительная модель. Основу модели составил идеальный источник угловой скорости с программируемым номиналом. На его валу укреплено устройство коммутации (многоканальный барабан переключений). В зависимости от угла поворота в соответствии с предустановленной программой, а это – 120-, 150- или 180-градусная коммутация, барабан формирует управление для транзисторов стоек силового трехфазного моста, осуществляя синтез напряжений, питающих статор двигателя. Двигатель и идеальный источник угловой скорости имеют общий вал. Какой бы момент ни создавал вентильный двигатель – во всех режимах вал крутит идеальный источник угловой скорости, характеризующийся бесконечной мощностью и нулевым внутренним сопротивлением. Например, для снятия естественной механической характеристики вентильного двигателя скорость увеличивается линейно от нуля до номинальной.

Поставленные вычислительные эксперименты проводились при угле коммутации, равном нулю. Магнитная составляющая тока, I d , была положительной. Токи пусковые. Статор глубоко насыщен. Поэтому цепь влияния магнитной составляющей тока на момент, в библиотечной, линейной, модели СДПМ программы Simulink была отключена (во всех режимах ψ _m был принят равным константе).

Для удобства представим скорость и момент также в относительных единицах, приняв за базовые значения каждого способа питания уже принятые базовые величины, а расчёт проведём для различных значений относительной индуктивности ^ = ^^ б . Это позволит нам независимо от параметров двигателей оценить влияние индуктивности на их характеристики при различных способах коммутации. Для определённости, в качестве объекта исследований был взят моментный двигатель МД-500 со следующими параметрами:

• –    напряжение постоянного тока U _п = 24 В;

• –    активное сопротивление фазной обмотки R = 1 Ом;

• –    индуктивность фазной обмотки L = 0,5 мГн;

• –    максимальное потокосцепление поля ротора Ф_т = 0,04 Вб;

• – число пар полюсов р = 5.

Численный эксперимент проводился при нулевой, номинальной и завышенной в десять раз индуктивности статорной обмотки.

Расчёт характеристик и моделирование электромагнитных процессов в приводе

Случай нулевой индуктивности рассеяния статорной обмотки нереален, тем не менее он позволяет дать наглядную сравнительную оценку для различных способов питания с точки зрения элек- трических потерь, вида механических характеристик и пульсаций момента. По представленным выше уравнениям рассчитаны МХ и ЭХ (рис. 2 и 3).

Пульсации момента лучше также представить в относительном виде

δ= ^μн с ,                                             (9)

μ где примем μн и μс соответственно момент в начале и в середине МКИ, определяемые по уравнениям (8).

Результаты расчета представлены на рис. 4 и 5.

Анализ кривых, представленных на рис. 2 и 3, позволяет заключить, что при нулевой индуктивности:

– МХ линейны для всех способов питания ВД;

– с точки зрения энергетических показателей в широком диапазоне изменения скоростей враще-

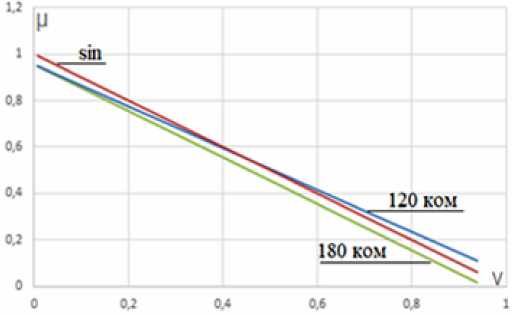
Рис. 2. Механическая характеристика при L = 0

Fig. 2. Mechanical characteristic at L = 0

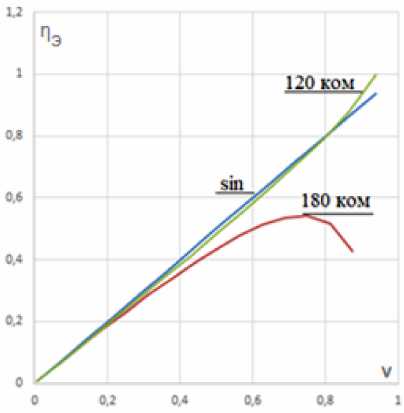
Рис. 3. Энергетическая характеристика при L = 0

Fig. 3. Energy characteristic at L = 0

c)

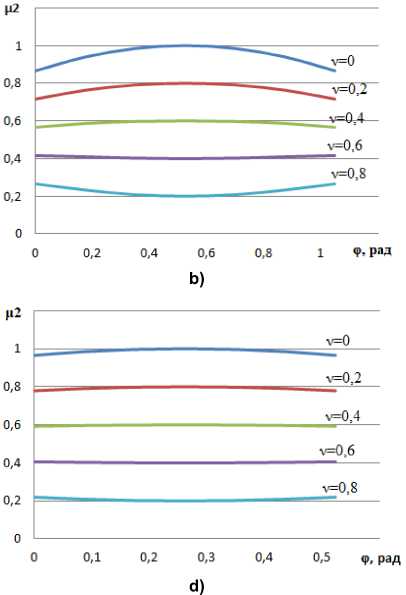
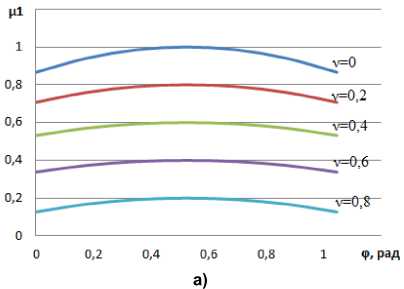
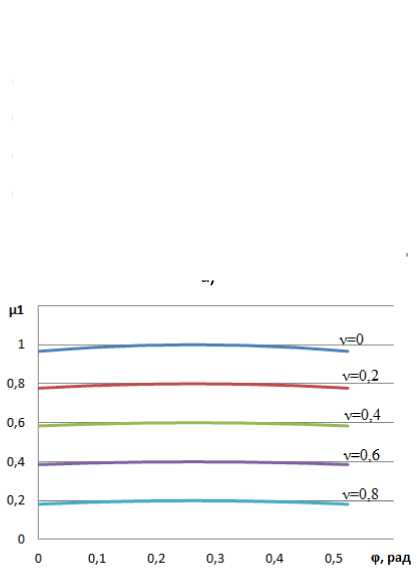
Рис. 4. Кривая изменения момента в течение МКИ: а – 6-тактная 180-градусная коммутация; b – 6-тактная 120-градусная коммутация; c – 12-тактный интервал, соответствующий рис. 1а; d – 12-тактный интервал, соответствующий рис. 1b

Fig. 4. Torque change curve during MKI: a – 6-stroke 180-degree switching; b – 6-stroke 120-degree switching; c – 12-clock interval corresponding to Fig. 1a; d – 12-clock interval corresponding to Fig. 1b

c)

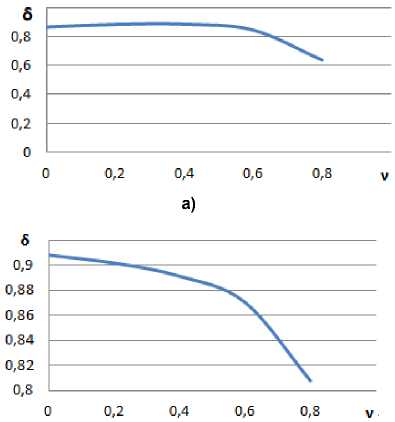
Рис. 5. Кривая пульсаций момента: а – 6-тактная 180-градусная коммутация; b – 6-тактная 120-градусная коммутация; c – 12-тактный интервал, соответствующий рис. 1а; d – 12-тактный интервал, соответствующий рис. 1b Fig. 5. Torque ripple curve: a – 6-stroke 180-degree commutation; b – 6-stroke 120-degree commutation;

c – 12 clock interval corresponding to Fig. 1a; d – 12 clock interval corresponding to Fig. 1b

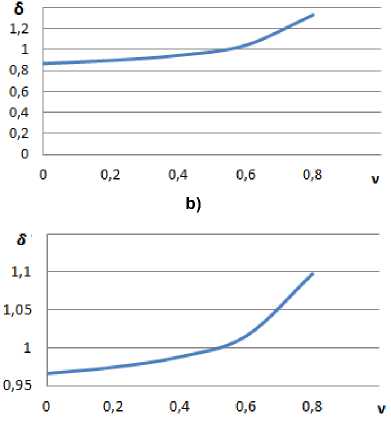
d)

ния привода наиболее предпочтительна дискретная 120- градусная коммутация;

– с точки зрения пульсаций момента несомненное преимущество имеет синусоидальное питание, а из дискретных способов предпочтительна 150-градусная коммутация.

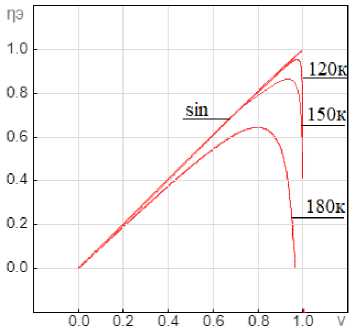
Результаты исследования привода на модели с учётом индуктивности обмотки представлены в виде кривых μ = f (ω), η э = f (ω) для каждого способа коммутации и различных значениях относительной индуктивности (рис. 6, 7).

Анализ этих кривых позволяет заключить, что с ростом относительной индуктивности внешний вид МХ и ЭХ становится качественно одинаковым при всех способах питания двигателя. Однако лучшую линейность и большее значение электромагнитного КПД по сравнению со всеми способами питания даёт 120-градуcная коммутация.

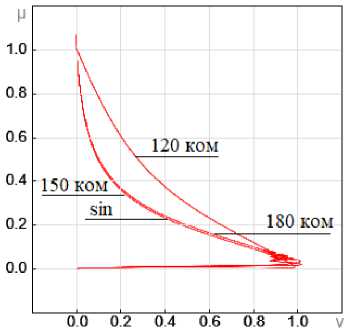
Что касается пульсаций момента, то нас интересует количественное отличие их при различных способах коммутации, разных относительных индуктивностях и разных скоростях вращения. Поэтому картинка пульсаций момента по результатам моделирования представлена в виде годографа момента в процессе разгона двигателя от нулевой скорости до ν = 0,3 (рис. 8, 9).

Анализ годографов позволяет заключить:

– как и ожидалось, минимальные пульсации момента получим при 150-градусной коммутации;

– наибольшие пульсации момента имеем при 180-градусной коммутации;

– с ростом относительной индуктивности пульсации увеличиваются;

а)

Рис. 6. Энергетическая характеристика при ξ = 0,5 (а) и ξ = 5 (b)

Fig. 6. Energy characteristic at ξ = 0.5 (а) and ξ = 5 (b)

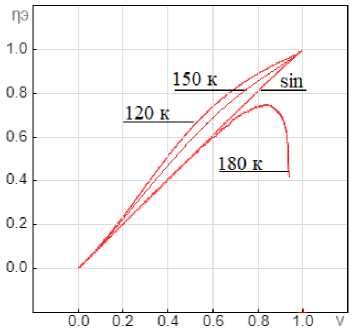
b)

а)

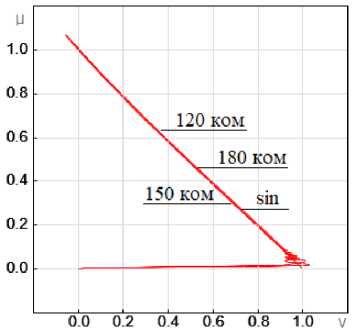
Рис. 7. Механическая характеристика при ξ = 0,5 (а) и ξ = 5 (b)

Fig. 7. Mechanical characteristic at ξ = 0.5 (а) and ξ = 5 (b)

b)

а)

b)

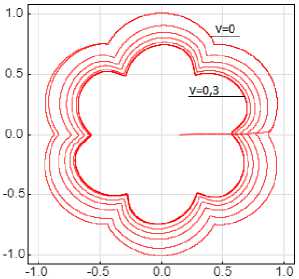
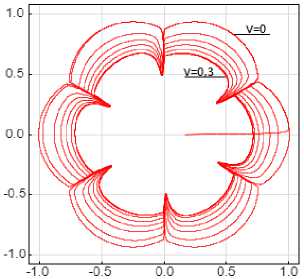
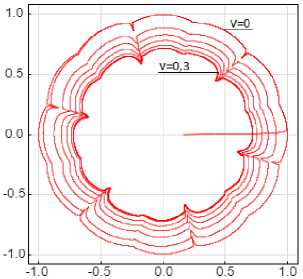
Рис. 8. Годографы момента при ξ = 0,5: а – 180-градусная коммутация; b – 120-градусная коммутация; c – 150-градусная коммутация

Fig. 8. Hodographs of the moment at ξ = 0.5: a – 180-degree switching;

b – 120-degree switching; c – 150-degree switching

c)

а)                                                 b)                                                 c)

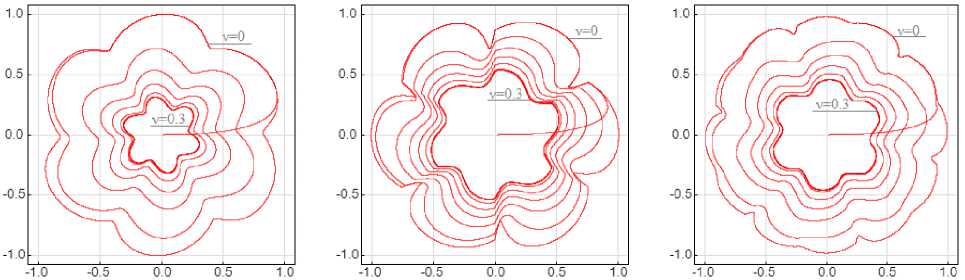
Рис. 9. Годографы момента при ξ = 5: а – 180-градусная коммутация; b – 120-градусная коммутация; c – 150-градусная коммутация Fig. 9. Hodographs of the moment at ξ = 5: a – 180-degree switching; b – 120-degree switching; c – 150-degree switching

– пульсации увеличиваются также и с ростом скорости;

– количественно и качественно пульсации момента при нулевой индуктивности примерно совпадают с пульсациями при ненулевой индуктивно- сти, особенно это проявляется при небольших относительных скоростях вращения (до ν ≈ 0,5), когда они приближаются к нулю;

– при увеличении относительной индуктивности становится существенным влияние вызванных коммутационными процессами дополнительных пульсаций тока, следовательно, и момента (см. рис. 8 и 9).

Практическая часть

Результаты проведённого анализа позволяют решать практические задачи выбора способа питания СДПМ в режиме вентильного двигателя в зависимости от основных технических требований. В частности:

– если определяющим является требование обеспечения максимального значения электромагнитного КПД, лучше использовать дискретную 120-градусную коммутацию;

– в случае жёстких требований по пульсациям момента необходимо использовать синусоидальное питание;

– если мы хотим получить низкие пульсации и использовать более простую схему с дискретной коммутацией, рекомендуется применять 150-градусную двенадцатитактную коммутацию;

– ожидаемые пульсации момента в приводе во всём диапазоне скоростей и для всех способов коммутации приближённо можно просто определить по кривым рис. 5.

– результаты исследований можно уверенно распространить на приводы с мощностями до десятков кВт;

– в двигателях в сотни кВт активное сопротивление обмотки оказывается пренебрежительно мало, поэтому дискретная коммутация приводит к значительным выбросам энергии через обратные вентили инвертора и оказывается неэффективной.

Заключение

Сравнительная оценка различных способов питания СДПМ в режиме вентильного двигателя позволяет сделать вывод о том, что в целом ряде общепромышленных механизмов и машин, где нет жёстких ограничений по пульсациям момента – насосы, вентиляторы, транспортёры и др., – с успехом может быть использована простая и более экономичная по энергопотреблению по сравнению с синусоидальным питанием дискретная 120-градусная коммутация. В том случае, если имеются ограничения по пульсациям момента на уровне не более 5 % можно использовать 150-градусную дискретную коммутацию, при более жёстких требованиях лучше использовать синусоидальное питание.