Сравнительное исследование спектральных свойств асферических линз

Использование асферических рефракционных линз позволяет получить изображающие системы с высоким качеством изображения, т.к. введение асферической линзы в объектив позволяет минимизировать большинство геометрических аберраций. К сожалению, процесс изготовления асферических рефракционных линз высокого качества весьма трудоёмок, вследствие этого асферическую рефракционную оптику нельзя использовать в массовых дешёвых устройствах. С другой стороны, изготовление дифракционных аналогов асферических линз по трудоёмкости ничем не отличается от изготовления дифракционных аналогов сферических линз. Однако использование только дифракционных линз для изображающей оптики затруднено из-за высокой хроматической аберрации [1 – 7]. Поэтому в настоящее время дифракционные линзы применяются либо в системах, где используется одна длина волны [8, 9], либо только для компенсации хроматической аберрации рефракционных изображающих систем [10– 13]. В некоторых случаях с помощью дифракционной линзы компенсируют не только хроматические аберрации, но и часть геометрических аберраций рефракционной изображающей системы [11]. Для этого необходимо использовать существенно асферические линзы.

В настоящей работе рассматривается расчёт дифракционного аксикона с переменным периодом (ак-слинзы), при этом зависимость периода от радиуса такова, что этот аксикон работает аналогично идеальной линзе, которая в геометрооптическом приближении собирает все лучи в одну точку.

1. Расчёт фазовой функции дифракционного аксикона с изменяющимся периодом (акслинзы)

Рассмотрим расчёт дифракционного аксикона с изменяющимся периодом, так, чтобы он формировал фокус в одной точке аналогично идеальной линзе в рефракционном варианте (рис. 1).

Для расчётов будем рассматривать аксикон как радиальную дифракционную решётку с непрерывно

меняющимся периодом. Из условия схождения лучей в одну точку имеем условие:

r - f tg β= 0∼ tg β= r / f .

Здесь f – фокусное расстояние. Для дифракционной решётки с периодом D имеется соотношение, определяющее направления на максимумы амплитуды:

D sin β = M λ ∼ tg β = M λ / ^D ² - M ² λ ² . (2)

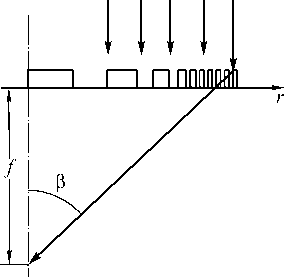
Рис. 1. Схема прохождения лучей света через аксикон с изменяющимся периодом

Здесь M – номер максимума (порядка дифракции), λ – длина волны падающего излучения. Приравнивая два выражения для тангенса угла, после преобразований получим выражение для текущего периода:

₃ 7 r ² + f ²

D ( r ) = M λ          .                          (3)

r

Зная период, находим фазовую функцию элемента:

ψ ( r ) = - k     r =

D ( r )

k

⋅

M

r ²

7 r ² + f ²

где k = 2 π/λ .

Оценим хроматизм элемента (4). Для этого осветим элемент, изготовленный для длины волны λ₀ , длиной волны λ . Определим новое положение фокуса L .

L = f ( λ ) = r / tg β ( λ );

tg P ( X ) = M X / V D ²( X ₀ ) - M ²X ² =

= Xr / VX0 f2 + r2(%0 -X2).

Получим фокус

L = 7 X0 f2+r 2(%0-X2)

A f  ^V (2 f + R 7 f ).

X ₀

Минимум выражения в скобках при заданном радиусе будет при f = R /72 ~ в = 54,74 ° .

То есть фокус не просто смещается, но и перестаёт быть точкой, так как правая часть равенства зависит от r . При этом даже при наличии чистого смещения есть несимметрия положения новых фокусов относительно исходного при симметрии длин волн: X = X ₀ ±AX .

Перепишем выражение для «фокуса» в виде

L ( r )    » J¹ + ■ ( 1 -X ²/ X 0 ) .                    (6)

^X v ^f

Мы видим, что наличие корня ещё больше усиливает смещение. При X > X ₀ L ( R ) <  L (0), а при X < X ₀ - L ( R ) >  L (0); здесь R - радиус элемента. Длина фокального отрезка A L = | L ( R ) - L (0)|.

Если можно приблизить корень двумя слагаемыми ряда Тейлора, то получим:

L ( r ) ^ [1 + f ( 1 -X 2 / X 0 ) 1 ;

2 L f               J                   (7)al ” f1 -X2/X0|.

И в таком приближении имеется нелинейность, поэтому середина фокального отрезка не соответствует среднему радиусу элемента.

Возьмём в качестве меры хроматизма расстояние A f между центрами фокальных отрезков для X 1 = X ₀ - AX и X ₂ = X ₀ + AX . Общее выражение выписывать не будем, ограничимся случаем применимости приближения (7). Тогда центр первого отрезка будет в точке

X0 f X1

1 + f (2 AX / X0 -(AX)2/ X0)

а второго – в точке

X0 f X2

1 - f (2AX / X0 +(AX)2/ X0)

(8а)

(8б)

Расстояние между этими центрами равно

X f X f

0 V          0 V I

"X  XT

+Rf X(2AX-(AX)2 /X0) + X-(2AX + (AX)2 /X0)

Если дополнительно предположить, что разброс длин волн небольшой, то получаем достаточно простое выражение

2. Результаты моделирования

В данном разделе численно исследуются свойства трёх фокусирующих элементов:

– сферической (идеальной рефракционной) линзы:

T sph ( r ) = exp ( - ik^r 2 + f 2 ) ,                      (10а)

– параболической линзы:

Tpar(r) = exP (-ik(r72f)),                      (10б)

– акслинзы:

Taxl (r) = exp (-ik(r 7 Vr 2 + f 2 )) .

(10в)

Заметим, что акслинза, как и сферическая линза, при малом фокусе будет стремиться к высокоапертурному аксикону:

^T ax ^{( r} )    _f ^ 0 >  exp (^{- ikr} ) .

Известно, что параболическая линза (10б) получается из (10а) в параксиальном случае при учёте двух слагаемых в разложении Тейлора. Если же учесть три слагаемых (что соответствует уже не совсем параксиальному случаю), то вместо (10а) можно записать:

T sph _ p (r) = exP

- ik

r

r

-

2 f

8 f ³

Можно рассматривать выражение (12) как параболическую функцию пропускания со сферической аберрацией. Если же разложить функцию пропускания акслинзы (10в), удерживая только два слагаемых, то получим:

T axl _ p (r) = exP

Из (13) видно, что в параксиальном случае имеется несоответствие фокусов акслинзы с остальными элементами, поэтому далее будем для акслинзы использовать несколько иную функцию пропускания (с удвоенным фокусом):

^T axl 2⁽ r ) = exP

- ,k

V

V r2 +(2 f )2

В этом случае вместо (13) получим:

^T axl 2_ p ⁽ r ) = exP

( r ²      r ⁴

ik

V 2 f 16 f³

что фактически соответствует идеальной (рефракционной) линзе, но с уменьшенной сферической аберрацией.

Для наглядного сравнения линз (10а) и (14) можно записать следующее равенство:

I r2 2 = Vr2 +(2f )2 - . (2f) 2 V r2 +(2 f)                  V r2 +(2 f)

Таким образом, акслинза (14) представляет собой идеальную линзу с удвоенным фокусом, комбинированную с некоторым дополнительным элементом. Тем не менее, в параксиальном случае все три элемента работают практически одинаково. На рис. 2 показаны результаты хроматической дисперсии при использовании любой бинарной линзы (10а)–(10в) радиусом 5 мм с фокусным расстоянием f = 300 мм для изображения осевой точки, удалённой от линзы на расстояние 50000 мм при длинах волн излучения 1 0 = 0,55 мкм, 1 1 = 0,45 мкм, X 2 = 0,65 мкм.

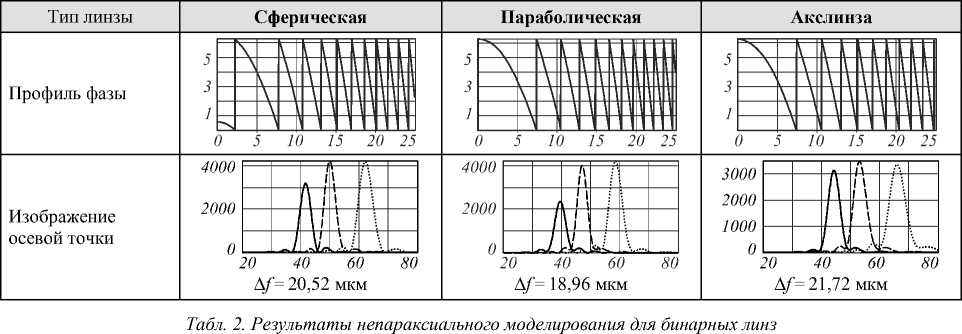
В табл. 1 приведены результаты моделирования для многоуровневых линз радиусом 25 мкм с фокусом 50 мкм. В табл. 2 показаны аналогичные результаты для бинарных линз.

• 3 . Эксперимент

Фазовая функция аксикона с изменяющимся периодом была рассчитана для фокусного расстояния 160 мм на длину волны 550 нм для апертуры диаметром 8 мм. Такая линзы была изготовлена методом прямой лазерной записи по фоторезисту на станции лазерной записи. На рис. 3 представлен вид рельефа в центральной области линзы (рис. 3а) и краевой об-

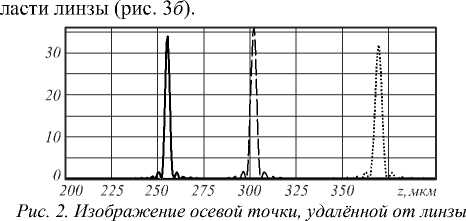
на расстояние 50000 мм, при длинах волн излучения

Л ₀=0,55 мкм (зелёный цвет), Л 1 0,45 мкм (синий цвет), Л 2 =0,65 мкм (красный цвет)

Табл. 1. Результаты непараксиального моделирования для многоуровневых линз

Тип линзы

Сферическая

Параболическая

Акслинза

Профиль фазы

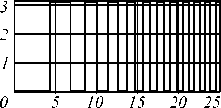
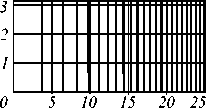
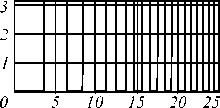
Изображение осевой точки

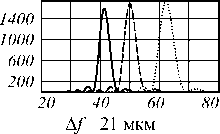
Как видно из рис. 3, получившийся микрорельеф хорошего качества, без сбоев и неоднородностей.

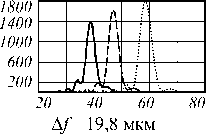
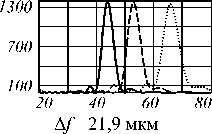
Для изготовленной линзы была экспериментально построена функция рассеяния точки (ФРТ). Для этого пучок твердотельного лазера проецировался на матовый экран, расположенный на расстоянии 4 м от линзы, а затем с помощью изготовленной акслинзы строилось изображение этого пятна. Размер пятна, сфокусированного на экран, составил около 0,3 мм, т.е. его можно считать на таком удалении от линзы точечным источником света. В качестве линзы для сравнения использовалась дифракционная параболическая линза с фокусным расстоянием 160 мм. Для регистрации изображений была использована матрица с разрешением 1600×1200 с размером пиксела 5,65 мкм. На рис. 4 приведены изображения пятна, полученные с помощью дифракционной параболической линзы (рис. 4а, в) и акслинзы (рис. 4б, г). На рис. 4а, б приведены пятна рассеяния при оптимальном значении яркости для определения ширины ФРТ. На рис. 4в, г яр- кость светового пятна была увеличена, чтобы за счёт расширения его изображения (камера регистрирует те участки светового пятна, которые ранее не регистрировались из-за недостаточной чувствительности матрицы) можно было точнее определить соотношение размеров для ФРТ параболической дифракционной линзы и аксилинзы [15].

Ширина ФРТ по полуспаду интенсивности на рис. 4а – 23 мкм, на рис. 4б – 17 мкм. К сожалению, размер пятна всего 3-4 пиксела, и для более точного измерения надо использовать рис. 4в, г. Результаты измерений по рис. 4в, г дают более точное значение соотношения ширин ФРТ – ширина ФРТ для параболической линзы в 1,26 больше, чем у акслинзы. Т.е. в случае монохроматического источника света акслин-за работает лучше дифракционной параболической. Но, кроме геометрических аберраций, нужно также исследовать хроматические аберрации.

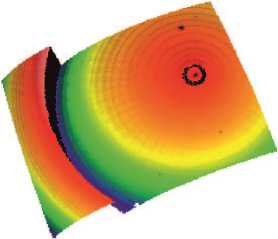
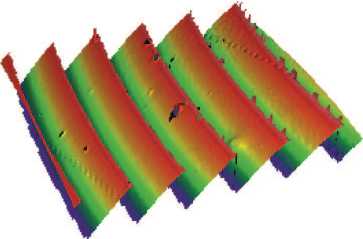
Рис. 3. Вид центрального (а) и краевого (б) участков микрорельефа дифракционной линзы

б)

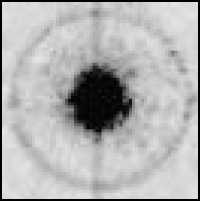
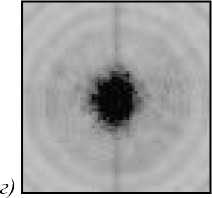
Рис. 4. Изображение точечного источника, построенное параболической линзой (а) и акслинзой (б) при оптимальном уровне яркости; изображение точечного источника, построенное параболической линзой (в) и акслинзой (г) при повышенном уровне яркости (негативные изображения)

Для этого акслинза была установлена в оптическую схему, представленную на рис. 5, в которой был проведён эксперимент по формированию изображения этим элементом. При этом расстояние от монитора до линзы составило 1,5 м.

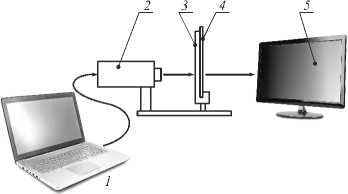
Рис. 5. Оптическая схема, позволяющая строить изображения с помощью дифракционных линз:

• 1    – компьютер, 2 – CCD-камера, 3 – диафрагма,

• 4    – дифракционная линза, 5 – монитор

Для исследования хроматических аберраций было использовано изображение файловой таблицы, которое непосредственно выводилось на монитор компьютера (рис. 6 а ). Для сравнения такое же изображение было сформировано с помощью дифракционной параболической линзы с такими же параметрами (рис. 6 б ).

Поскольку основное изображение файловой таблицы почти монохромно, то обе дифракционные структуры довольно качественно строят изображения. Но на изображении присутствует вертикальная линия белого цвета, которая содержит все RGB-компоненты, и поэтому вдоль неё на изображении мы видим довольно широкую цветную полосу. Очевидно, что по ширине этой полосы можно оценить вели- чину поперечной хроматической аберрации каждой из дифракционных структур. Так, для рис. 6а ширина этой линии – 400 мкм, а для рис. 6б – 260 мкм. Т.е. дифракционный аксикон с переменным периодом даёт хроматическую аберрацию в полтора раза больше, чем параболическая линза. Эта аберрация, как видно из рис. 6, полностью нивелирует эффект от уменьшения геометрических аберраций. И на той, и на другой картинке видны межпиксельные промежутки размером 0,2 мм. Но при съёмке в монохроматическом режиме, когда светофильтрами отсекается область спектра от 470 нм до 520 нм, влияние хроматической аберрации уменьшается (рис. 7).

Как видно из рис. 7, по разрешающей способности акслинза сравнялась с линзой параболической, но контраст изображения, полученного с её помощью, всё же ниже, чем контраст изображения, полученного параболической линзой.

Заключение

Проведён расчёт дифракционной асферической линзы, которая обеспечивает фокусировку в одну точку. Экспериментально показано, что такая линза действительно для монохроматического источника позволяет получить существенно более узкую ФРТ.

Однако по результатам проведённых теоретических расчётов и натурного эксперимента можно сделать вывод, что наличие повышенно хроматической аберрации у идеальной дифракционной линзы полностью нивелирует эффект от компенсации части гео- метрических аберраций. Следовательно, повышать для немонохроматического света с использованием разрешение изображающих дифракционных систем одного дифракционного элемента невозможно.

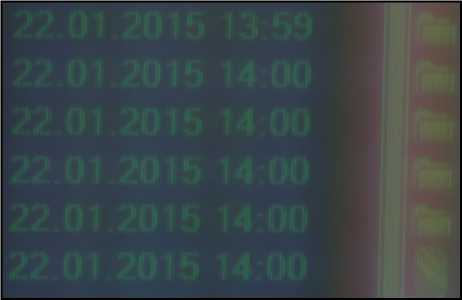
Рис. 6. Изображение рабочего окна программы Windows Comander, снятое с экрана монитора дифракционной идеальной линзой (а) и дифракционной параболической линзой (б) с фокусными расстояниями 160 мм с расстояния 1,5 м

б)

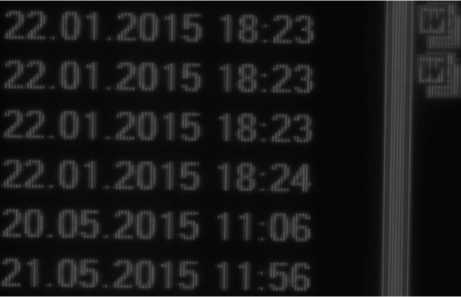
Рис. 7. Изображение рабочего окна программы Windows Comander, снятое с экрана монитора дифракционной идеальной линзой (а) и дифракционной параболической линзой (б) с фокусными расстояниями 160 мм с расстояния 1,5 м при съёмке

в монохроматическом режиме

Работа выполнена при финансовой поддержке Российского научного фонда (грант 14-31-00014).