Сравнительное моделирование амплитудной и фазовой зонных пластинок

Френелевская зонная пластинка (ЗП) известна в оптике много лет (смотри избранные статьи по ЗП [1]). Однако строгий анализ фазовых и амплитудных ЗП с короткими фокусными расстояниями, формирующих субволновые фокусные пятна в видимой и инфракрасной области спектра, стал проводиться относительно недавно. В [2] с помощью численного моделирования показано, что серебряная ЗП толщиной h=300 нм с фокусным расстоянием f=0,5 мкм (длина волны λ =633 нм) формирует субволновое фокусное пятно c диаметром по полуспаду интенсивности (Full Width of Half Maximum) FWHM=0,39λ. В аналогичной статье [3] на основе численного расчёта сравнивали рабочие характеристики ЗП из серебра, золота, алюминия и вольфрама. Показано, что максимальную интенсивность в фокусе имеет серебряная ЗП (дифракционная эффективность составляет 40 %), а минимальный диаметр пятна наблюдается у ЗП из вольфрама (FWHM=0,52λ). В [4] численно показано, что многослойная ЗП из 5 слоёв кварца и серебра толщиной по 30 нм увеличивает интенсивность фокуса в 10 раз по сравнению с ЗП из одного слоя. Увеличение интенсивности фокуса объясняется вкладом плазмонных мод. Остальные параметры ЗП в [4] такие же, как в [2, 3]. В [5 – 7] разрабатываются приближённые теории амплитудных и фазовых ЗП, предсказания которых сравниваются со строгим численным моделированием. В [8] теоретически исследуется эффект затенения в фазовой ЗП. Показано, что для ЗП с коротким фокусом (NA>0,7) из-за эффекта затенения интенсивность в фокусе уменьшается в 2 раза. Заметим, что дифракционная эффективность фазовой ЗП с фокусом, равным длине волны f= λ, равна 46 % [3].

В предыдущих работах авторов [9 – 13] численно и экспериментально исследовалась бинарная ЗП диаметром 14 мкм, с фокусным расстоянием f= λ =532 нм, которая фокусировала линейно-поляризованный и радиально-поляризованный лазерный свет в субволновое фокусное пятно. Минимальный размер фокусного пятна, достигнутый экспериментально, был равен (0,35×0,38)λ [13].

В данной работе с помощью FDTD-метода (Finite Difference Time Domain method) исследуются бинарные амплитудные зонные пластинки Френеля из серебра с толщиной 20 нм и хрома с толщиной 30 нм. В предыдущих работах такие ультратонкие ЗП не исследовались. Показано, что учёт дисперсии материала (кварца, серебра и хрома) в рамках модели Селмейера и Друде–Лоренца приводит к изменению параметров фокусного пятна не больше, чем на 6 %. Размеры фокусных пятен для фазовой и амплитудной ЗП почти одинаковые (все пятна имеют субволновый размер от 0,41 до 0,47 от длины волны), отличие только в меньшей (в 3 раза) максимальной интенсивности в фокусе. Важно отметить, что фазовую ЗП изготовить труднее, чем амплитудную, из-за разницы в аспектном отношении (в 30 раз больше). У фокусного пятна ЗП из хрома обнаружено почти полное отсутствие первых боковых лепестков, что увеличивает отношение сиг-нал/шум в микроскопии. Также обнаружены вблизи колец ЗП из серебра локальные максимумы, интенсивность которых сравнима с интенсивностью в фокусе и которые объясняются возбуждением поверхностных плазмон-поляритонов.

Амплитудная зонная пластинка

Рассмотрим фазовую ЗП, выполненную из кварцев ого стекла и обладающую восемью зонами (рис. 1).

SiO2

пппп__П п пЪ

SiO2

-ra -r6 -r4   -r,                 r2 1'4 r6 rs

Рис. 1. Фазовая ЗП

Радиус зон легко рассчитать по стандартной формуле:

Г т = V m X f + m ^214 ,                        (1)

где r_m - радиус m -й зоны, мкм; X - длина волны, нм; f – фокусное расстояние.

Высота рельефа рассчитывается по формуле:

h = %/ 2 ( n - 1 ) ,                                     (2)

где n – коэффициент преломления материала.

Построим пластинку с восемью зонами для фокусировки излучения с длиной волны 2 = 532 нм со следующими характеристиками: f =532 нм, h =532 нм, m = 8 (для расчёта h использовался коэффициент преломления n = 1,5). В табл. 1 приведены радиусы зон, рассчитанные по формуле (1).

Табл. 1. Радиусы зон

m	1	2	3	4
r m , нм	595	921	1219	1505
m	5	6	7	8
r m , нм	1784	2060	2334	2606

Данную ЗП будем считать эталоном для сравнения. Проведём моделирование процесса фокусировки линейно-поляризованного света (направление поляризации вдоль оси y ) с длиной волны 532 нм через описанную выше ЗП. Моделирование проводилось с помощью коммерческого пакета FullWAVE, реализующего FDTD-метод, с учётом и без учёта частотной дисперсии ( n = 1,5 ). Зависимость диэлектрической проницаемости от частоты для кварцевого стекла описывалась с помощью модели Селмейера (табл. 2) [14]:

^е ( л ) ^е । £

m

^Ае m % ²

^ ^- ^ m ^- i ^П m

где λ – длина волны; ε ∞ (x,z) – диэлектрическая проницаемость на высоких частотах; Δε m (x,z) – величина резонанса; λ m (x,z) – резонансная длина волны; η m (x,z) – коэффициент демпфирования.

Табл. 2. Параметры модели Селмейера для кварцевого стекла

m	Δε m, мкм	λ m, мкм	η m, мкм
1	0,69616630	0,068404300	0
2	0,40794260	0,11624140	0
3	0,89747940	9,8961610	0
ε ∞ = 1

Учёт дисперсии материала производится потому, что моделирование дифракции монохроматической волны FDTD-методом фактически состоит в моделировании дифракции импульса с прямоугольной огибающей с длиной в несколько десятков длин волн. Для центральной длины волны 532 нм это соответствует импульсу длительностью в несколько десятков фемтосекунд. В ходе анализа результатов здесь и далее проводилось усреднение рассчитанной интенсивности поля по 20 периодам излучения.

Для моделирования использовались следующие параметры сетки: h x = λ/30 нм, h y = λ/30 нм, h z = λ/30 нм, h _T = 10 - шаги дискретизации по пространству и времени. Данные шаги обеспечивают сходимость численного метода, а дальнейшее уменьшение шага не приводит к существенным изменениям (СКО менее 0,001 %). Результаты моделирования представлены на рис. 2 и в табл. 5.

На рис. 2 приведено распределение интенсивности в фокусе вдоль направлений, перпендикулярных направлению распространения света. Разная ширина фокусного пятна по разным декартовым осям (рис. 2 а и рис. 2 б ) объясняется линейной поляризацией фокусируемого пучка. Этот эффект хорошо известен и объяснён теоретически, например, в [15]. В направлении поляризации (ось y ) в формирование фокуса вносят вклад и поперечная, и продольная составляющие напряжённости электрического поля, а в поперечном направлении (ось x ) вклад вносит только поперечная составляющая напряжённости электрического поля.

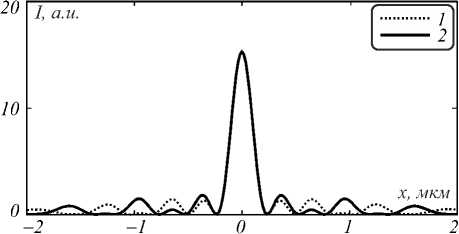
б)

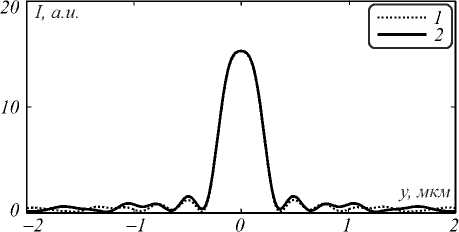
Рис. 2. Распределение интенсивности в фокусе для фазовой ЗП вдоль x (a) и y (б) для случаев без учёта (линия 1) и с учётом (линия 2) частотной дисперсии

Из рис. 2 видно, что распределение интенсивности в фокусе, полученное с помощью моделирования FDTD-методами с учётом и без учёта дисперсии, практически совпадают. СКО составило 7,5 % (такая цифра обусловлена расхождениями в лепестках).

Амплитудная зонная пластинка из серебра

Рассмотрим амплитудную ЗП, полученную путём структурирования плёнки металла, напылённой на кварцевую подложку (рис. 3).

Проведём моделирование процесса фокусировки линейно-поляризованного света с длиной волны 532 нм через амплитудную ЗП с помощью коммерческого пакета FullWAVE с учётом и без учёта частотной дисперсии. Для учёта зависимости диэлектрической проницаемости металлов воспользуемся моделью Друде–Лоренца [16]:

to2

е (x, z, to) = е (x, z) + ——-—^ + -2 г tov-to2

+ z m

Am tom -to2 - 2ito8m +tom

где ω – частота; ω p – плазменная частота; ν – частота столкновений, A m – амплитуда резонанса, δ m – коэффициент демпфирования, ω m – резонансная частота.

: :           8Ю^               :

"Г8 -Г6 -V4 -Г'              Г2 Гб Гб Г8

Рис. 3. Амплитудная ЗП

Изначально было промоделировано распространение света через ЗП с рельефом из серебра ( n = 2,66+4,16 i ) и высотой рельефа 20 нанометров. Параметры модели Друде для серебра: ω _p = 41,94605, ν = 0,243097. Параметры модели Лоренца для серебра приведены в табл. 3.

Табл. 3. Параметры модели Лоренца для серебра

m	A m , Гц	δ m , , Гц	ω m , Гц
1	7,924697	19,68071	4,132646
2	0,501327	2,289161	22,6941
3	0,013329	0,329194	41,45307
4	0,826552	4,639097	46,001
5	1,113336	12,25	102,759

Для моделирования использовались следующие параметры сетки: h_x = λ/30 нм, h_y = λ/30 нм, h z = λ/30 нм, h τ = 10 – шаги дискретизации по пространству и времени.

На рис. 4. приведено распределение интенсивности в фокусе вдоль направлений, перпендикулярных направлению распространения света.

Из рис. 4 видно, что распределение интенсивности в фокусе, полученное с помощью моделирования FDTD-методами с учётом и без учёта дисперсии, практически совпадают. СКО составило 1,75 %.

Амплитудная зонная пластинка из хрома

Теперь рассмотрим ЗП c рельефом из хрома (n = 0,143 + 3,05 i ) и высотой рельефа 30 нм. Проведём моделирование процесса фокусировки линейно-поляризованного света с длиной волны 532 нм через амплитудную ЗП с помощью коммерческого пакета FullWAVE с учётом и без учёта частотной дисперсии. Для учёта зависимости диэлектрической проницаемости металлов воспользуемся моделью Друде–Лоренца (4). Параметры модели Друде для хрома: ω _p = 22,31521, ν = 0,238032. Параметры модели Лоренца для хрома приведены в табл. 4.

Табл. 4. Параметры модели Лоренца для хрома

m	A m , Гц	δ m , , Гц	ω m , Гц
1	1191,853	16,07984	0,612807
2	58,79069	6,609194	2,750032
3	34,21399	13,55265	9,977106
1	1,238159	6,761129	44,44113

Для моделирования использовались следующие параметры сетки: h x = λ/30 нм, h y = λ/30 нм, h z = λ/30 нм, h _τ = 10 – шаги дискретизации по пространству и времени.

На рис. 5 приведено распределение интенсивности в фокусе вдоль направлений, перпендикулярных направлению распространения света.

Из рис. 5 видно, что распределение интенсивности в фокусе, полученное с помощью моделирования FDTD-методами с учётом и без учёта дисперсии, практически совпадают. СКО составило 4,5 % (такая цифра обусловлена расхождениями в центре фокусного пятна). Видно также (рис. 5 а ), что рядом с фокусным пятном вдоль оси x почти отсутствуют первые боковые лепестки. При сканировании таким фокусным пятном вдоль оси x , например, в конфокальном микроскопе, увеличивается отношение сиг-нал/шум при обнаружении микро- и нанообъектов.

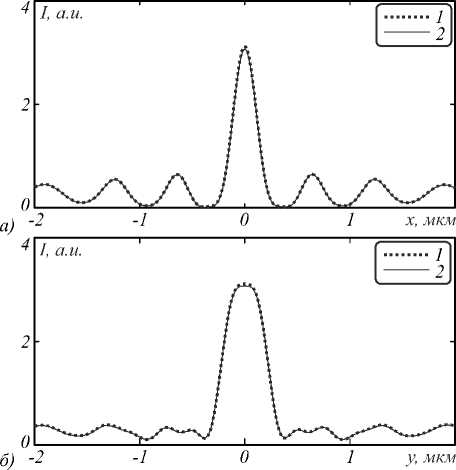
Рис. 4. Распределение интенсивности в фокусе для фазовой ЗП вдоль x (a) и y (б) для случаев без учёта (линия 1) и с учётом (линия 2) частотной дисперсии

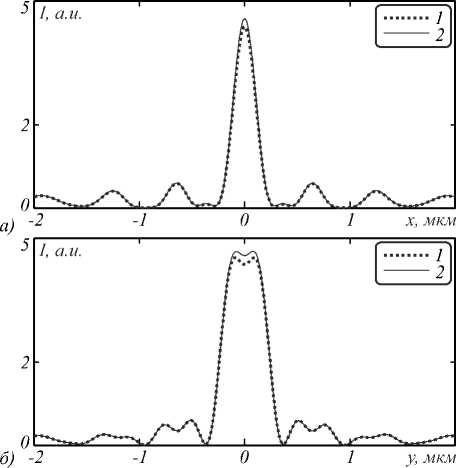
Рис. 5. Распределение интенсивности в фокусе для фазовой ЗП вдоль x (a) и y (б) для случаев без учёта (линия 1) и с учётом (линия 2) частотной дисперсии

В табл. 5-6 приведены характеристики фокусных пятен, формируемых моделируемыми ЗП. Во второй колонке таблицы указан «реальный фокус», соответствующий максимуму интенсивности на оптической оси. Можно видеть, что расстояние до максимума интенсивности на оптической оси отличается от геометрического фокусного расстояния f =532 нм.

Табл. 5. Результаты моделирования без учёта дисперсии

Мат-л	f , нм	FWHM , λ x,	FWHM y , λ	Imax , a.u.
SiO 2	500	0,41 λ	0,79 λ	15,22
Ag	700	0,47 λ	0,84 λ	3,11
Cr	600	0,46 λ	0,87 λ	4,39

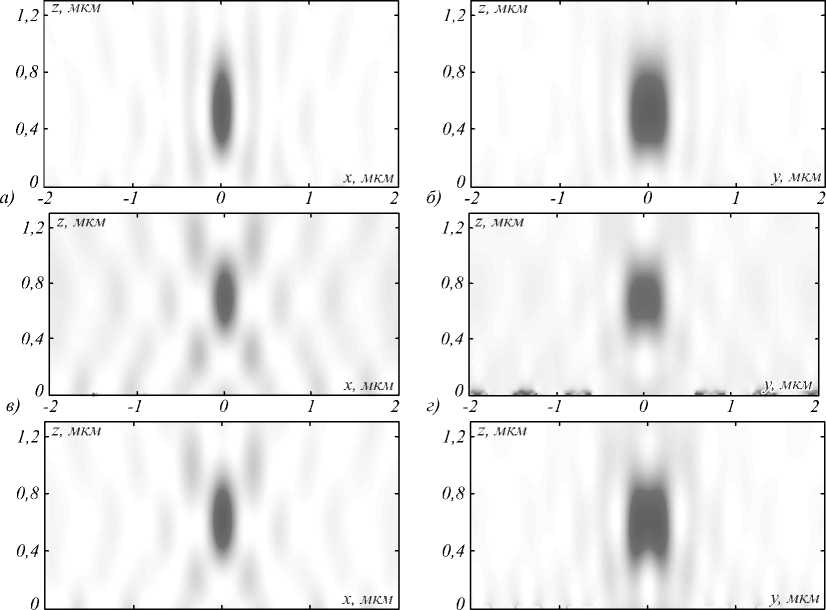
На рис. 6 представлены картины дифракции линейно-поляризованного лазерного излучения на всех вышепредставленных ЗП, полученные с учётом частотной дисперсии.

Табл. 6. Результаты моделирования с учётом дисперсии

Мат-л	f , нм	FWHM , λ x,	FWHM y , λ	Imax , a.u.
SiO 2	500	0,41 λ	0,80 λ	15,35
Ag	700	0,48 λ	0,85 λ	3,07
Cr	600	0,45 λ	0,87 λ	4,58

Из рис. 3–5 и табл. 5–6 видно, что фазовая ЗП и амплитудная ЗП из хрома формируют достаточно похожие по геометрическим размерам фокусные пятна. При этом интенсивность в фокусе для амплитудной ЗП падает всего в 3,4 раза. Точно изготовить амплитудную ЗП проще, чем фазовую ЗП. В следующей статье мы планируем детально сравнить экспериментальные результаты по субволновой фокусировке лазерного излучения, полученные с помощью изготовленных ЗП из хрома и серебра с указанными выше характеристиками, с приведёнными здесь расчётными данными.

д) -2

е)   -2

-1

О

-1

О и из хрома (д) и (е) ЗП

Рис. 6. Распределение интенсивности в плоскостях ZX и ZY для фазовой (а) и (б), амплитудых из серебра (в) и (г)

На рис. 6 г видны локальные максимумы интенсивности вблизи участков плёнки серебра вдоль оси Y (рис. 6 г ). Вдоль оси X подобные локальные максимумы практически отсутствуют (рис. 6 в ). На рис. 7 показано распределение интенсивности вблизи ЗП из серебра вдоль оси Y. Наличие таких субволновых локальных максимумов интенсивности объясняется возбуждением плазмонных мод в ультратонких полосках серебра. Этот эффект для ультратонких полосок серебра (наноантенны) известен [17], но у ЗП он ранее не упоминался. Видно, что величина интенсивности этих поверхностных плазмон-поляритонов такая же (3,6 условных единиц), как интенсивность в фокусе (3,2 условных единиц).

Заключение

В работе с помощью FDTD-метода проведено сравнительное моделирование острой фокусировки лазерного света с помощью бинарных фазовой и амплитудных ЗП, состоящих из колец металла высотой 20 –30 нм, находящихся на прозрачной подложке из кварца. Показано, что учёт дисперсии материала (кварца, серебра и хрома) приводит к изменению параметров фокусного пятна не больше, чем на 6 % (рис. 3–5). Размеры фокусных пятен для фазовой и амплитудной ЗП почти одинаковые, отличие только в меньшей (в 3 раза) максимальной интенсивности в фокусе (табл. 5, 6). При этом фазовую ЗП изготовить труднее, чем амплитудную, из-за разницы в аспектном отношении (в 30 раз больше). У фокусного пятна ЗП из хрома обнаружено почти полное отсутствие первых боковых лепестков (рис. 5а), что увеличивает отношение сиг-нал/шум в микроскопии. Также обнаружены вблизи колец ЗП из серебра локальные субволновые максимумы, интенсивность которых сравнима с интенсивностью в фокусе и которые объясняются возбуждением плазмонных мод в ультратонких полосках серебра (рис. 7).

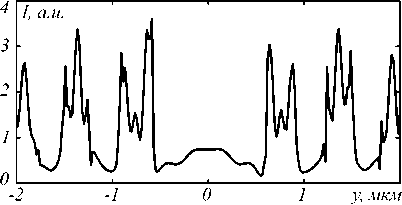
Рис. 7. Распределение интенсивности вблизи ЗП из серебра вдоль оси Y

Работа выполнена при поддержке Министерства образования и науки РФ, гранта Президента РФ поддержки ведущих научных школ (НШ-3970.2014.9) и молодого кандидата наук (МК.-4816.2014.2), а также грантов РФФИ (14-07-31092, 14-07-97039, 14-2907133, 14-07-31218, 15-07-01174).