Сравнительное моделирование двумя методами острой фокусировки зонной пластинкой

В последние годы возрос интерес к уменьшению размеров фокального пятна или к острой фокусировке света. Преодоление дифракционного предела актуально в литографии [1], оптической микроманипуляции и оптических системах памяти [2]. Под преодолением дифракционного предела в данной работе подразумевается получение фокального пятна с шириной по полуспаду интенсивности меньшей FWHM = 0,51λ/NA, где λ – длина волны света, NA – числовая апертура, FWHM=full width at half maximum.

Преодолеть дифракционный предел можно двумя способами: 1) увеличением боковых лепестков в картине дифракции (например, с помощью использования кольцевой диафрагмы можно сформировать пучок Бесселя, для которого дифракционный предел в 1,4 раза меньше FWHM = 0,36λ /NA) и 2) при фокусировке вблизи поверхности раздела сред, где присутствуют поверхностные затухающие волны, конструктивная интерференция которых может уменьшить диаметр фокусного пятна ниже предела. В данной работе рассматривается фокусировка радиально-поляризованного света на расстоянии от поверхности больше длины волны, и поэтому преодоление дифракционного предела возможно только первым способом. При острой фокусировке радиально-поляризованного света основной вклад в формирование фокуса даёт продольная компонента вектора напряжённости электрического поля, которая пропорциональна функции Бесселя нулевого порядка J ₀ ( k NA r ).

Ранее было замечено, что использование радиально-поляризованного света позволяет получить фокальное пятно с размерами меньшими, чем при фокусировке линейно-поляризованного света [3], а в [4] показано, что при фокусировке света объективом с числовой апертурой большей NA=0,8 радиально-поляризованный свет даёт пятно меньшее, чем свет с круговой поляризацией.

В качестве фокусирующего элемента в данной работе будет использоваться зонная пластинка (ЗП). В

[5] с помощью ЗП было получено фокальное пятно с диаметром 0,42λ, а в статье [6] показано, что добавление к ЗП фазовой пластинки, состоящей из трёх кольцевых зон, позволяет уменьшить размер пятна до 0,37λ. В вышеназванных работах при моделировании фокусировки используются формулы Ричардса-Вольфа (РВ) [7], модифицированные для радиально-поляризованного света [8]. Необходимо отметить, что векторная теория Дебая [9], на которой основаны РВ-формулы, справедлива только при фокусных расстояниях много больших длины волны. На расстояниях же, сопоставимых с длиной волны, следует использовать, например, метод FDTD (= finite difference time domain), представляющий собой численное решение уравнений Максвелла [10] и в настоящее время получивший широкое распространение благодаря своей универсальности. Применительно к острой фокусировке света зонными пластинками данный метод используется, в частности, для расчёта фокусировки света с помощью плазмонных линз. Так, в [11] теоретически с помощью FDTD и экспериментально с помощью ближнепольной оптической микроскопии демонстрируется преодоление дифракционного предела плазмонной линзой (диаметр пятна по полуспаду интенсивности теоретически FWHM=0,41λ, экспериментально 0,48λ). В [12] с помощью FDTD метода для плазмонной линзы получено фокальное пятно шириной 0,33λ, а в работе [13] численно показана возможность фокусировки в ближнем поле с помощью простой фазовой ЗП (диаметр пятна при этом равен 0,52λ). В [14] анализируются фокусирующие свойства амплитудной ЗП.

Целью данной работы является сравнение результатов моделирования фокусировки радиально-поляризованной моды R-TEM01 ЗП с помощью двух различных методов: R-FDTD и по РВ-формулам. Тем самым делается попытка нахождения границ применимости РВ-формул. Необходимо отметить, что ранее уже делались попытки сравнения этих двух методов – в [15] было показано согласование значений диаметра фокального пятна, полученного при фоку- сировке ЗП Бессель-Гауссова пучка, однако вопрос о границах применимости РВ-формул детально не рассматривался. В данной работе показано, что оба метода демонстрируют возможность преодоления ЗП с радиусом R =20λ дифракционного предела при освещении её модой R-TEM01 с радиусом ω = 10λ. При расчёте методом FDTD преодоление дифракционного предела наблюдается для числовой апертуры большей NA=0,97 (f = 4,7λ, где f – фокусное расстояние ЗП), а по РВ-формулам – большей NA=0,96 (f = 5,4λ). Относительная погрешность результатов вычисления диаметра фокального пятна этими двумя методами при этом не превышает 6%.

Формулы Ричардса-Вольфа для радиально-поляризованного света

Нами моделировалось прохождение радиально-поляризованной моды R-TEM 01 [16] с длиной волны λ = 0,532 мкм через стеклянную бинарную ЗП с показателем преломления n = 1,5, радиусом R =20λ и высотой рельефа h = λ/2( n -1) = 0,532 мкм. Радиусы ЗП вычислялись по известной формуле (рис. 1):

r m ²= m λ f + m ²λ²/4, (1) где f – фокусное расстояние зонной пластинки, m – целое число.

к Z, МКМ

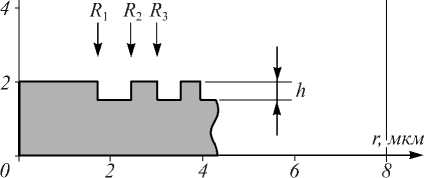
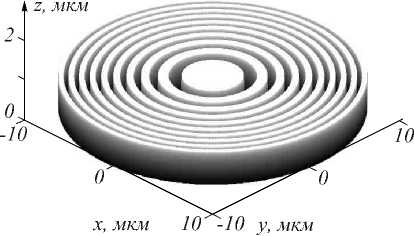
Рис. 1. Профиль (а) и объёмное изображение (б) зонной пластинки с фокусным расстоянием f = 15λ

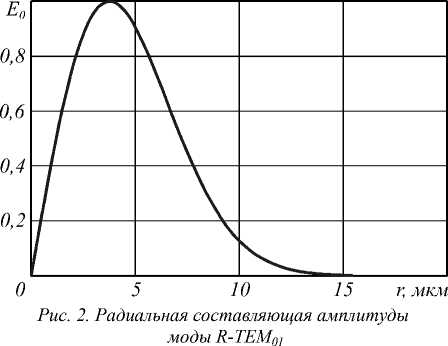
Радиальная составляющая амплитуды моды

R-TEM01 имеет вид (рис. 2):

f r2 1

E_r = Ar exp ^I ,                              (2)

I » I

где r – радиальная координата, ω = 10λ – радиус Гауссова пучка, A – нормировочный множитель, как видно из рис. 2, он подбирался так, чтобы максимум амплитуды был равен единице.

Формулы Ричардса-Вольфа для радиально-поляризованного света в области фокуса имеют вид [7]:

θ

Er ( r , z ) = A ^max T ( θ ) B ( θ )sin(2 θ ) l 0 ( θ ) × 0

× J ₁( kr sin θ )exp{ ikz cos θ }d θ ,

E ( r , z ) = 2 iA ^θmax T ( θ ) B ( θ )sin²( θ ) l ( θ ) × z ₀

× J ₀( kr sin θ ) exp{ ikz cos θ }d θ ,

где l ₀(θ) – начальное распределение электрической составляющей поля в координатах выходного зрачка, J p ( x ) – функция Бесселя порядка p , T (θ) – функция аподизации зрачка (для ЗП T (θ) = cos^-3/2θ [5]), B (θ) – функция комплексного пропускания ЗП, A – константа, θ max = arcsin (NA) – максимальный угол, определяемый числовой апертурой зонной пластинки (для зонной пластинки числовая апертура NA = sin (arctg ( R / f ))).

Для того чтобы получить начальное распределение в координатах выходного зрачка, необходимо воспользоваться соотношением:

l 0 ( ρ ) = l 0 ( fg ( θ )),

где l 0 (ρ) – начальное распределение поля в цилиндрической системе координат, g (θ) – функция проекции луча, для ЗП она имеет вид g (θ) =tg(θ) [17]. Таким образом, мода R-TEM₀₁ в координатах выходного зрачка для ЗП примет вид:

l ₀( θ ) = A 'tg θ exp

e0tg26 1

tg26 I

max

где β₀ = R /ω – параметр моды.

Функция пропускания фазовой зонной пластинки имеет вид B (θ) = exp{ i φ(θ)}, где φ(θ) = φ FZP – φ apl . φ FZP (θ) – фазовая функция зонной пластинки, φ FZP (θ) = π m для θ m < θ < θ m +1 , где m – номер зоны. φ apl (θ)= kf / cosθ – kf . [6]

При моделировании методом FDTD использовалась модификация метода, предназначенная для расчёта прохождения радиально-поляризованного света через объекты, обладающие радиальной симметрией. Вид конечно-разностных формул, используемых в расчётах, приведён в [18].

Результаты моделирования

Моделировалась фокусировка моды R-TEM 01 зонной пластинкой с разными фокусными расстояниями (λ ≤ f ≤ 15λ). На рис. 3 а показана зависимость изменения диаметра фокального пятна по полуспаду интенсивности от фокусного расстояния ЗП для двух методов – FDTD (кривая 1) и по РВ-формулам (кривая 2). На рис. 3 б аналогично показана зависимость изменения продольной ширины фокального пятна (глубины резкости фокуса) по полуспаду интенсивности от фокусного расстояния.

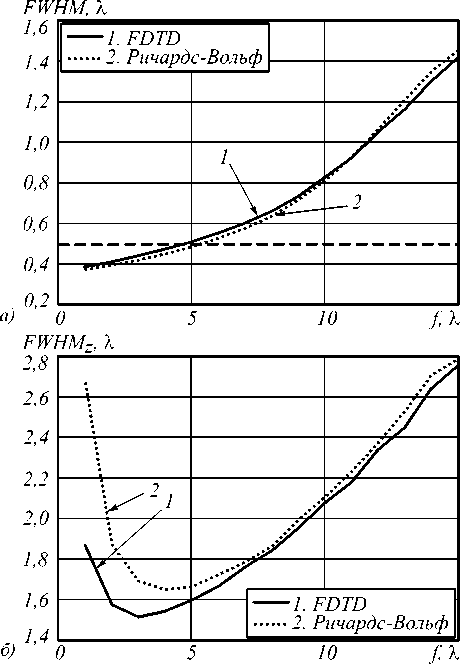
Рис. 3. Зависимость изменения диаметра фокального пятна FWHM (а) и продольной ширины фокального пятна FWHMz по полуспаду интенсивности (б) от фокусного расстояния зонной пластинки с радиусом R = 20λ при освещении её радиально-поляризованной модой R-TEM01 с ω = 10λ. Моделирование с помощью метода FDTD (кривая 1) и по РВ-формулам (кривая 2). Пунктирной кривой на рис. 3а отмечен дифракционный предел

Параметры моделирования FDTD-методом: дискретность разбиения по пространству λ/50, дискретность разбиения по времени λ/100 c , где с – скорость света в вакууме, на границах области помещались поглощающие слои Беренгера толщиной λ.

Относительное отклонение δ диаметра фокусного пятна, вычисленного FDTD-методом и по РВ-формулам, не превышало 6% (рис. 4, кривая 1), а относительное отклонение глубины фокуса FWHMz возрастало при уменьшении фокусного расстояния до 30% при f = λ (рис. 4, кривая 2). При фокусном расстоянии большем f ≥ 4λ (NA ≤ 0,98) обе ошибки не превышают 6%. Таким образом, можно утверждать, что РВ-формулы могут найти применение при моделировании острой фокусировки света, если фокус ЗП находится на расстоянии от поверхности большем, чем 4λ.

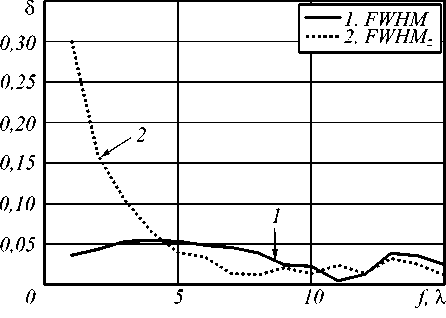
Рис. 4. Зависимость относительной ошибки вычисления диаметра фокального пятна (кривая 1) и продольной ширины фокального пятна (кривая 2) от фокусного расстояния зонной пластинки

Как видно из рис. 3 а , оба метода показывают преодоление дифракционного предела. При расчёте методом R-FDTD преодоление дифракционного предела наблюдается для фокусного расстояния f = 4,7λ (NA = 0,97), а по РВ-формулам – при f = 5,4λ (NA = 0,96). Минимальные значения диаметров фокальных пятен составили FWHM = 0,37λ при расчёте по РВ-формулам и FWHM = 0,39λ при расчёте методом FDTD (согласуется с [15]) для числовой апертуры NA = 0,999 ( f = λ). На рис. 5 приведено распределение интенсивности в фокальной плоскости для зонной пластинки с фокусным расстоянием f = λ. Преодоление дифракционного предела происходит за счёт увеличения энергии боковых лепестков и уменьшения эффективности фокусировки из-за аберрации ЗП с высокой числовой апертурой. Из рис. 3 б видно, что глубина фокусировки, рассчитанная FDTD-методом (кривая 1), всегда меньше, чем рассчитанная РВ-формулами (кривая 2). Это объясняется тем, что ЗП своей поверхностью ограничивает световой пучок в продольном направлении. Это хорошо видно из рис. 5 б .

Из рис. 3 б видно также, что наблюдается минимальное значение продольной ширины фокуса – при моделировании методом FDTD оно составило FWHM z = 1,51λ для фокусного расстояния f = 3λ (NA = 0,99), при расчёте по РВ-формулам FWHM_z = 1,65λ для фокусного расстояния f = 4λ (NA = 0,98).

Эффективность фокусировки можно оценить, м как n = W1/W0, где W0 = J\Er |2 r dr - энергия входного 0

пучка, E_r – радиальная составляющая амплитуды r ₀

моды R-TEM qi (рис. 2), W 1 = J I_FDTDr d r - энергия в 0

фокусе, IFDTD – распределение интенсивности в фо- кусе (рис. 5а), r0 = 0,4λ – точка первого минимума функции IFDTD. При фокусировке моды с радиусом ω = 10λ зонной пластинкой с фокусным расстоянием f = λ и радиусом R = 20λ эффективность фокусировки составила η = 5%.

Интенсивность, отн.ед.

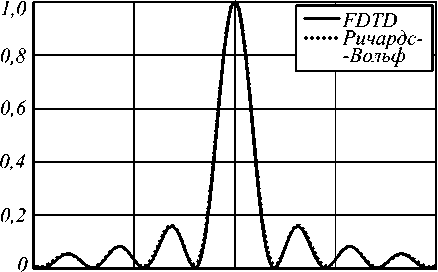
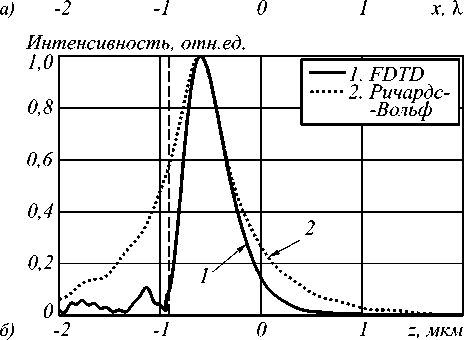
Рис. 5. Распределение интенсивности в фокальной плоскости вдоль оси x (а) и вдоль оси симметрии ЗП с радиусом R = 20λ и фокусным расстоянием f = λ (б) при освещении её радиально-поляризованной модой R-TEM01 с ω = 10λ. Моделирование с помощью метода FDTD (кривая 1) и по РВ-формулам (кривая 2). Пунктирной вертикальной прямой на рис. 5б отмечен край ЗП

Полученные нами результаты находятся в согласии с результатами работы [15], где с помощью РВ-формул и методом FDTD было получено пятно с диаметром FWHM=0,39λ при освещении зонной пластинки радиально-поляризованным Бессель-Га-уссовым пучком. В статье [5] также с помощью РВ-формул при фокусировке ЗП с числовой апертурой NA=0,98 было получено фокальное пятно с шириной FWHM=0,42λ. В нашем случае для числовой апертуры NA=0,98 (она достигается, когда радиус ЗП R =20λ и фокусное расстояние f =4λ) вычисление по РВ-формулам даёт аналогичный результат, если радиус моды равен ω = 15λ. Моделирование методом FDTD для таких параметров зонной пластинки и входного пучка показало, что диаметр пятна равен FWHM=0,44λ. Таким образом, относительная погрешность вычисления FWHM равна 4,55%. Если же радиус моды уменьшить до ω = 10λ, то моделирование методом FDTD показывает увеличение диаметра пятна до FWHM=0,47λ.

Для проверки зависимости влияния радиуса зонной пластинки на результаты фокусировки было проведено моделирование только методом FDTD для радиусов зонной пластинки R = 15λ и R =25λ при неизменных параметрах освещающего пучка. На рис. 6

показаны результаты.

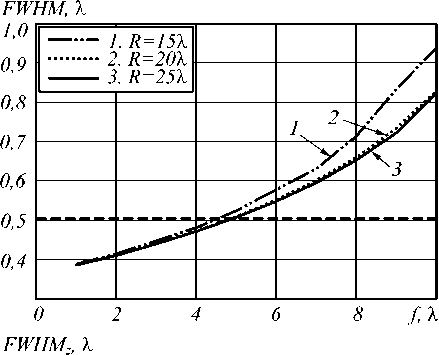
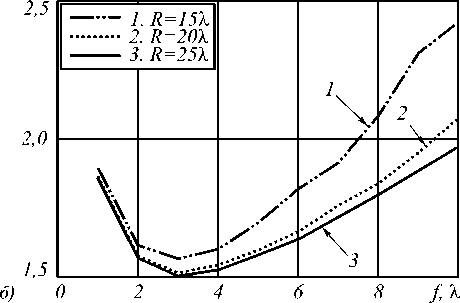
Рис. 6. Зависимость диаметра фокального пятна по полуспаду интенсивности (а) и продольной ширины фокального пятна по полуспаду интенсивности (б) от фокусного расстояния ЗП с радиусом R = 15λ (кривая 1), R = 20λ (кривая 2) и R = 25λ (кривая 3) при освещении её радиально-поляризованной модой R-TEM 01 с ω = 10λ

Как видно из рис. 6, увеличение радиуса зонной пластинки при неизменных параметрах освещающего пучка приводит к уменьшению диаметра фокального пятна. Однако при R > 20λ диаметр фокального пятна почти не изменяется (кривые 2 и 3 на рис. 6 а ). Это означает, что значение радиуса ЗП R = 20λ и радиуса пучка ω = 10λ выбраны оптимальным образом. На рис. 7 показаны результаты зависимости влияния ширины освещающего пучка на величину диаметра фокального пятна по полуспаду интенсивности (рис. 7 а ) и продольной ширины фокального пятна по полуспаду интенсивности (рис. 7 б ).

Как видно из рис. 7, увеличение радиуса освещающего пучка ω приводит к уменьшению диаметра пятна. Хотя происходит это нелинейным образом. Так, увеличение ω в 1,5 раза (кривые 2 и 3 на рис. 7а) приводит к уменьшению диаметра фокального пятна на 20…25% при f > 6λ и почти не меняет диаметр фо- кального пятна при f < 2λ. А глубина фокуса при f > 6λ почти не меняется (кривые 2 и 3 на рис. 7б).

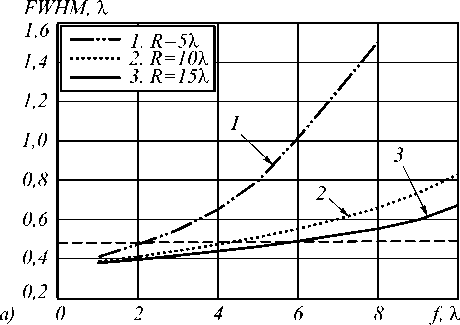
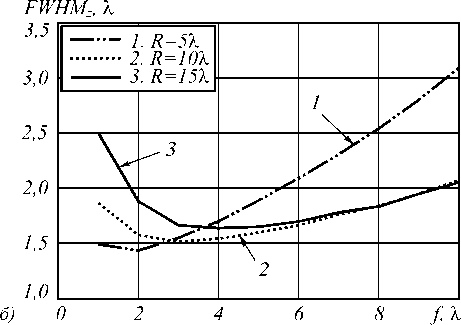
Рис. 7. Зависимость диаметра фокального пятна по полуспаду интенсивности (а) и продольной ширины фокального пятна по полуспаду интенсивности (б) от фокусного расстояния ЗП с радиусом R = 20λ при освещении её радиально-поляризованной модой R-TEM01 с ω = 5λ (кривая 1), ω = 10λ (кривая 2) и ω = 15λ (кривая 3)

Фазовые ЗП, подобные используемым в моделировании, могут быть изготовлены, например, с использованием плазмо-химического травления на кварце. На рис. 8 приведена зависимость ширины последней ступеньки ЗП с радиусом 20λ от фокусного расстояния. Минимальная ширина последней ступеньки при моделировании соответствовала ЗП с фокусным расстоянием f = λ и была равна 266 нм. Это значение доступно для современной электронной литографии.

Заключение

В данной работе были получены следующие результаты:

– Значения диаметров фокальных пятен, получаемых при прохождении радиально-поляризованной моды R-TEM₀₁ с радиусом ω = 10λ и длиной волны λ = 0,532 мкм через стеклянную ( n = 1,5) фазовую ЗП с радиусом 20λ, глубиной рельефа h = 0,532 мкм и фокусным расстоянием λ≤ f ≤ 15 λ , согласуются друг с другом при моделировании методом R-FDTD и с помощью РВ-формул. При этом относительная погрешность значений диаметра фокусного пятна не превышает 6%.

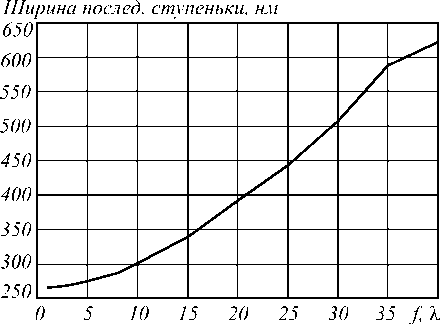
Рис. 8. Зависимость ширины последней ступеньки зонной пластинки с радиусом R = 20λ от фокусного расстояния f

– Установлены границы применения приближённого метода Ричардса-Вольфа: при фокусном расстоянии большем f ≥ 4λ (NA ≤ 0,98) относительные ошибки поперечного и продольного размеров фокусного пятна, рассчитанные FDTD-методом и по РВ-формулам, не превышают 6%.

– Оба метода (FDTD-метод и РВ-формулы) показывают преодоление дифракционного предела ЗП с радиусом R =20λ при освещении её радиально-поляризованной модой R-TEM₀₁ с радиусом ω = 10λ. При расчёте методом R-FDTD преодоление дифракционного предела (FWHM=0,51λ) наблюдается для числовой апертуры NA=0,97 ( f = 4,7λ), а по РВ-фор-мулам – при NA=0,96 ( f = 5,4λ).

– Минимальные значения полученных диаметров фокальных пятен составили FWHM=0,37λ (РВ-фор-мулы) и FWHM = 0,39λ (FDTD-метод) для фокусного расстояния f = λ.

– Оба метода показывают наличие минимального значения продольной ширины фокального пятна по полуспаду интенсивности. При этом продольная ширина фокального пятна по полуспаду интенсивности равна FWHM z = 1,51λ при моделировании методом R-FDTD и FWHM z = 1,65λ по РВ-формулам.

Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» (госконтракт № 14.740.11.0016), грантов Президента РФ поддержки ведущих научных школ (НШ-7414.2010.9) и молодого кандидата наук (МК-64571.2010.2).