Сравнительный анализ алгоритмов электронной компенсации дисперсии оптических сигналов
Автор: Бурдин Антон Владимирович, Григоров Игорь Вячеславович, Цвейбельман Евгения Львовна
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии телекоммуникаций
Статья в выпуске: 3 т.10, 2012 года.
Бесплатный доступ
Рассматриваются линейные и нелинейные алгоритмы электронной компенсации дисперсии сигналов в волоконно-оптических линиях передачи. При этом исследуются алгоритмы инверсной фильтрации с ограничением полосы частот и ограничением усиления, а также различных вариантов нелинейной фазовой фильтрации. Приводятся результаты моделирования и сравнительного анализа этих алгоритмов путем оценки эффективности компенсации дисперсии по критерию Релея.
Электронная компенсация дисперсии, нелинейный фазовый фильтр, инверсный фильтр, критерий релея, выигрыш по разрешению
Короткий адрес: https://sciup.org/140191564
IDR: 140191564 | УДК: 621.396.4
Текст научной статьи Сравнительный анализ алгоритмов электронной компенсации дисперсии оптических сигналов
В современных волоконно-оптических линиях передачи (ВОЛП) одним из основных факторов, ограничивающих скорость передачи, является дисперсия. Для уменьшения дисперсионных искажений сигналов применяются различные методы, в том числе и алгоритмы электронной компенсации дисперсии. Рассмотрим вкратце простейший метод – инверсную фильтрацию [1]. Представим процесс компенсации дисперсии сигнала JOY прошедшего канал связи, как процесс восстановления сигнала, прошедшего некоторую линейной систему с импульсной характеристикой g^f) , которую можно условно назвать порождающим фильтром [2] – см. рис.1.
Рис. 1. Схема процесса восстановления сигнала
Сигнал на его выходе определяется сверткой
/(0^g(0®5(0. (1)
Пусть входной сигнал имеет бесконечно малую длительность, то есть
0 = 3(0.
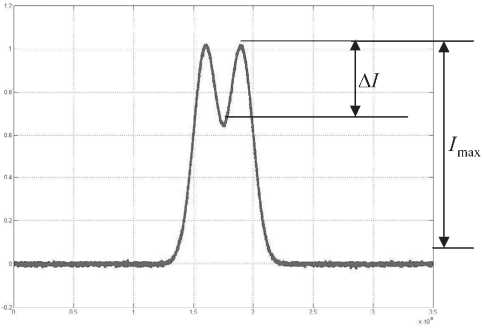
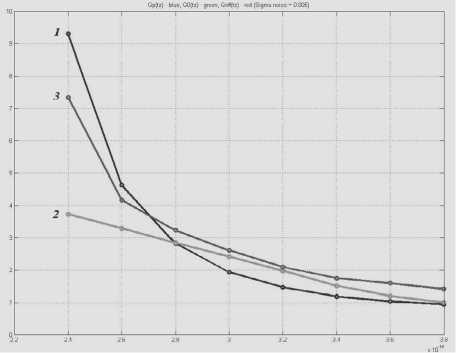
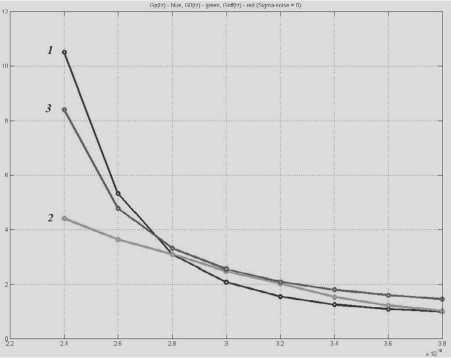
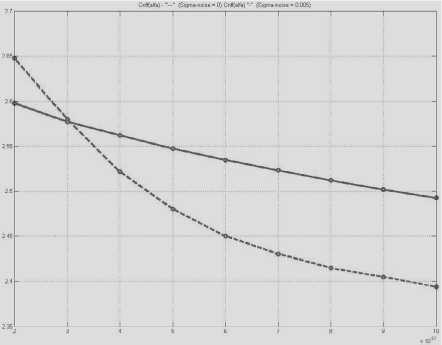
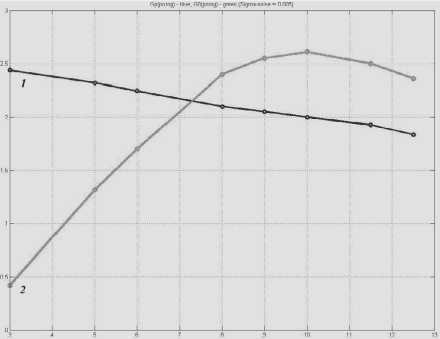
Для идеальной компенсации дисперсии сигнала / (0 необходимо, чтобы на выходе восстанавливающего фильтра с импульсной характеристикой Sb (0 сигнал совпадал с (2), то есть gBMwm=3 Применяя к обеим частям равенства (3) преобразование Фурье, получим К^Квкi®) = 1, где K\ito) и К B\\cY - передаточные функции порождающего и восстанавливающего фильтров. Следовательно, для идеальной компенсации дисперсии требуется восстанавливающий фильтр с передаточной функцией KB^ico) = i/ K(1(o) Фильтр с передаточной функцией (5) называется инверсным фильтром, а соответствующий процесс обработки, сигнала – инверсной фильтрацией. Главным недостатком инверсного фильтра является бесконечный рост коэффициента передачи на частотах нулей канала, что приводит к бесконечному усилению помехи. Поэтому рост функции (5) необходимо ограничивать. Для этого применяются различные фильтры, простейшими из которых являются инверсные фильтры с ограничением усиления и полосы частот [1]. Нелинейный алгоритм электронной компенсации дисперсии с применением нелинейных фазовых фильтров В [3] для решения задачи компенсации дисперсии предлагалось использовать нелинейный алгоритм обработки, построенный на основе модели в виде обобщенного нелинейного уравнения Шредингера i--= X^)^, (6) где Мч») - нелинейный дифференциальный оператор вида: М^)=Е(4)'^ ^т-я^)’ (7) r=2 ОТ аa – дисперсионные параметры порядка r. Данный алгоритм реализуется с помощью так называемых нелинейных фазовых фильтров (НФФ). Простейший НФФ содержит два фазовых звена – нелинейное и линейное. При этом нелинейное звено развивает внутри входного импульса внутриимпульсную частотную модуляцию, а линейное сжимает полученный импульс во времени аналогично сжатию частотно-моду-лированного сигнала в согласованном фильтре. Первое звено имеет характеристику преобразования мгновенных значений по комплексной огибающей: /f(v) = exp{i/(4')}. (8) здесь /(^) – нелинейная функция, определяющая закон изменения частоты внутри импульса, а второе звено имеет комплексный коэффициент передачи ' R G(i R =Пдад r=2 где Gr (i а Ат/ – параметр, характеризующий пространственную «длину» фильтра. В [4] показано, что для наилучшего временного сжатия импульсов необходимо, чтобы нелинейное звено развивало внутри импульса линейную частотную модуляцию. Для этого требуется, чтобы нелинейная функция Г^) входящая в (8), имела вид: /(Z)=-^>, (11) где 1^ = 2"\П (12) – функция, обратная функции Z(T), описывающей форму импульса. Например, для супергауссовского импульса Z(r) = (7 exp где 9 – показатель супергауссовости, оптимальная функция имеет вид 1 /(zh^L^ln^Y. (14) В частности, при q -1 импульс (13) переходит в гауссовский Z(0 = t/exp -^-y а нелинейность (14) – в логарифмическую: /(Z)=tiru2ln И Результаты моделирования алгоритмов компенсации дисперсии Рассмотренные выше алгоритмы обработки сигналов – инверсный фильтр с ограничением усиления и полосы частот и нелинейный фазовый фильтр с оптимальной нелинейностью (11) и квадратичной фазой, то есть при r = 2 в (10), были реализованы программно с использованием математического пакета «Matlab». На вход всех трех фильтров подавались одиночные импульсы гауссовской формы с различными параметрами, а также последовательности из нескольких таких импульсов. Количественно степень сжатия импульса можно оценить коэффициентом сжатия импульса на уровне его среднеквадратической полуширины. Как показано в [4], коэффициент сжатия импульса можно найти: К^=^ = ^ J|Z(r)|^_ где U и ^ – амплитуды импульсов на входе и выходе НФФ, g0 – постоянный коэффициент: 5o = 1 л •(18) л/4д"1«А т/ Для гауссовского импульса этот коэффициент имеет значение kc ^2aM] ' Очевидно, что степень сжатия импульса постоянной длительности определяется параметрами a и ^П . Для гауссовского импульса коэффициент (19) имеет значение около 5,5 и может быть существенно увеличен путем уменьшения aи Aq . Степень сжатия импульсов в инверсном фильтре с ограничением усиления и инверсном фильтре с ограничением полосы существенно ниже. Наибольший интерес представляет исследование степени разрешения импульсных сигналов, следующих друг за другом. Для количественной оценки эффективности компенсации дисперсии и разрешения сигналов при моделировании использовался критерий Релея [5]. Согласно этому критерию импульсы одина- ковой амплитуды считаются различимыми, если глубина «провала» между ними м составляет не менее 50% от их амплитуды I – см. рис. 2. Рис. 2. Оценка степени различимости импульсов по критерию Релея Рис. 4. Зависимости выигрышей по разрешению от задержки между импульсами при наличии шума для трех алгоритмов фильтрации: 1 – ИФ с ограничением усиления; 2 – ИФ с ограничением полосы частот; 3 – НФФ Рис. 3. Зависимости выигрышей по разрешению от задержки между импульсами при отсутствии шума для алгоритмов: 1 – ИФ с ограничением усиления; 2 – ИФ с ограничением полосы частот; 3 – НФФ Рис. 5. Зависимости выигрышей по разрешению НФФ от параметра a при наличии (штриховая линия) и отсутствии шума (сплошная линия) Оценим степень разрешения импульсных сигналов параметром: / ’ (20) Эффективность работы того или иного фильтра в задаче повышения степени разрешения можно оценить выигрышем по разрешению: R0M Rm где RmИ ^out – степени разрешения сигналов, соответственно, на входе и выходе фильтра. Графики зависимостей выигрышей по разрешению (21) от параметров сигналов и фильтров приведены на рис. 3-6. Выводы Из полученных результатов можно сделать следующие выводы. 1. Из всех рассмотренных алгоритмов НФФ в наименьшей степени искажает одиночные сигналы гауссовской формы и наиболее эффективно сжимает их во времени. 2. Наибольший выигрыш по разрешению для малых значений задержки между импульсами обеспечивает инверсный фильтр с ограничением полосы. 3. Если задержка между импульсами превышает значение 1,5 T , где T – среднеквадратическая полуширина входного импульса, то выигрыш по разрешению НФФ превышает выигрыш инверсных фильтров. Рис. 6. Зависимости выигрышей по разрешению инверсных фильтров от порога ограничения при наличии шума: 1 – ИФ с ограничением усиления; 2 – ИФ с ограничением полосы частот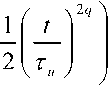
Список литературы Сравнительный анализ алгоритмов электронной компенсации дисперсии оптических сигналов
- Кловский Д.Д. Теория электрической связи. М.: Радиотехника, 2009. -647 с.
- Grigorov I.V. Nonlinear processing of signals on the basis of model in the form of generalized nonlinear Schrodinger equation. Proceedings of SPIE vol. 7374, 2009. -Р. 7374OH-01 -7374OH-08.
- Grigorov I.V. Research compressing of properties nonlinear phase filters. Proceedings of SPIE vol. 6605, 2006. -Р. 660505-01 -660505-08.
- Горячкин О.В. Лекции по статистической теории систем радиотехники и связи. М.: Радиотехника, 2008. -192 с.
- Василенко Г.И. Теория восстановления сигналов. М.: Сов. радио, 1979. -272 с.


