Сравнительный анализ диагонально-неявных методов Рунге – Кутты на одномерных модельных уравнениях газовой динамики

Одно из современных направлений развития вычислительной аэродинамики — вихре-разрешагощие методы расчёта турбулентных течений, такие, как метод крупных вихрей (LES — Large Eddy Simulation) и метод отсоединённых вихрей (DES — Detached Eddy Simulation) [1]. За счёт прямого разрешения крупномасштабной части движений газа эти методы позволяют более надёжно, чем подход Рейнольдса (RANS — Reynolds Averaged Navier-Stokes), описывать важные с инженерной точки зрения процессы, связанные с турбулентностью, и воспроизводить нестационарные явления, сопровождающие течение. Однако это достигается большой вычислительной ценой: вихреразрешающий расчёт требует использования трёхмерных сеток с характерными размерами ячеек, попадающими в инерционный интервал турбулентности, а интегрирование по времени должно вестить с таким шагом, чтобы эволюция всех представляющих интерес масштабов была воспроизведена корректно. В таких условиях предпочтение отдаётся численным методам, обладающим возможно меньшими диссипативными ошибками: по пространству — центрально-разностным схемам (или близким к ним по свойствам), а по времени — методам Рунге - Кутты достаточно высокого порядка аппроксимации [2].

Ситуация дополнительно осложняется в случае гибридного RANS/LES-расчёта. Для задач, решаемых гибридными методами, типичны сетки с сильными сгущениями к твердым поверхностям. Явные методы интегрирования по времени становятся неэффективными из-за слишком жёсткого ограничения на временной шаг, диктуемого наименьшими ячейками. Если не рассматривать такие экзотические подходы к решению этой проблемы, как метод дробного шага по времени [3], единственным выходом на сегодня остается применение неявных схем. Эти схемы неизбежно сглаживают нестационарные процессы вблизи стенок, где число Куранта¹ много больше единицы, но если диссипативные свойства схемы достаточно хороши, то, выбрав шаг по времени, пригодный для описания области развитой турбулентности, с такой схемой можно провести успешный вихреразрешающий расчёт. Исходя из сказанного, представляет интерес изучение неявных методов интегрирования по времени порядков аппроксимации выше первого, в частности, диагонально-неявных методов Рунге - Кутты (DIRK — Diagonally Implicit Runge - Kutta) [4], как возможных кандидатов для использования в гибридных RANS/LES-расчётах.

В настоящей статье исследуются свойства диагонально-неявных методов Рунге - Кутты при решении одномерных модельных уравнений. Рассматриваются методы DIRK высокого порядка точности с различными свойствами устойчивости. Показывается ограниченность использования уравнения переноса для сравнения методов. В серии расчётов по уравнению Бюргерса сравнивается уровень диссипативных ошибок, осцилляций решения, наблюдаемые порядки точности и особенности решений по различным методам класса DIRK.

'Число Куранта CFL = ст/h, где с — скорость переноса, h — шаг сетки. Это число показывает, па сколько ячеек сетки будет перенесено возмущение за шаг по времени.

Статья организована следующим образом. В разделе 2 описаны исследуемые методы. В разделе 3 рассматривается уравнение переноса, приводится сравнение методов по нему и обсуждаются его недостатки для анализа. В разделе 4 представлены результаты сравнения методов по уравнению Бюргерса. За ним следует заключительный раздел 5.

2.    Формулировка методов Рунге — Кутты2.1.    Общая формулировка методов Рунге — Кутты

Рассмотрим дифференциальное уравнение вида d«- d? = f (t,u),     u(0) = u0, u :[0,T] ^ Rm, f : [0,T] x Rm ^ Rm.

Зададим равномерную сетку {t_n}^₌₀ = {0, т, 2т,..., Nt = T}.

Рассмотрим один из способов построения методов Рунге - Кутты [4]. Пусть известно решение на n-м временном слое t_n и нужно найти u(t_n + т ). Для этого проинтегрируем уравнение (1) от t_n до t_n + т:

u(t_n + т )= u(t_n) + [ f (t,u(t)) dt.

^ n

Применим квадратурную формулу для вычисления интеграла в правой части. Пусть коэффициенты Ci определяют узлы этой квадратуры, g — их число, a bi — её веса, тогда

я

u(t_n + т ) = u(t_n) + T^bi f (tn + Ci т, u(t_n + Ci т )) + e,                  (2)

i =1

где e — ошибка квадратурной формулы. Аналогично, интегрируя (1) от t_n до t_n + c_iт, для решения в промежуточной точке u(t_n + Ciт ) можно получить

я

u(tn + CiT ) = u(tn) + T ^ ^aij f (tn + Cj T, u(tn + CjT )) + E,                (3)

7 =1

где dij — свои весовые коэффициенты.

Вводя обозначения tn +1 = tn + T,u_n = u(tn),u_ri+ 1 = u(tn + т), fi = f (tn + CiT,u(tn + CiT )) и подставляя (3) в (2), получим общий вид методов Рунге - Кутты:

я un +1 = un + T^bi fi, i =1

я fi = f(tn + Ci T,un + T^ciij fj), i = 1 ...g.

j =i

Здесь i — это номер стадии (или шага) Рунге - Кутты, a g — их число.

Коэффициенты методов Рунге - Кутты удобно представлять в виде таблицы Бутчера:

C1 *	c 11   • •              .	•    С 1 я *
* cя	• Ся 1   •	• сяя
	Ь 1     •	•     ья

Всего нужно определить g2 + 2g коэффициентов. Обычно ставится задача подобрать такие коэффициенты, чтобы достичь максимальной точности метода при выполнении некоторых условий (например, достижение определённых свойств устойчивости). Существует большое число семейств методов Рунге - Кутты. Их классификацию и способы нахождения соответствующих коэффициентов можно найти в книгах Бутчера [5] и Хайрера [6]. В настоящей работе исследуется один из классов этих методов — диагонально-неявные методы Рунге - Кутты (DIRK). В качестве эталонного будет использоваться один из более распространённых явных методов Рунге - Кутты.

2.2.    Формулировка явных методов Рунге — Кутты

В таблице Бутчера для явных методов диагональ и значения над ней заполнены нулями. В общем случае она имеет следующий вид:

С2

• •                 ••

«аа а                 а•

• ^Cq ^aq1   • • • ^aqq-1

• ^b1    • • • ^bqq-1 bq

2.3.    Формулировка диагонально-неявных методов Рунге Кутты

Таким образом, на каждой стадии методов Рунге - Кутты значение функции f в промежуточных точках явным образом выражается через уже известные значения:

г-1

fi = f (tn + CiT, U_n + T ^ Oij fj) , 1=1

благодаря чему вычисления идут быстро. Однако эти методы являются лишь условно устойчивыми, из-за чего при решении жёстких задач приходится сильно ограничивать шаг по времени [6].

В таблице Бутчера диагонально-неявных методов на главной диагонали присутствует хотя бы один ненулевой элемент:

• C 1 ац

• •                      •                  •

• •                 •                  •

• ^C q ^Oq1   ••• ^oqq

• ^b 1     • • • ^bq

2.4.    Исследуемые методы

На каждом временном шаге возникает система из q в общем случае нелинейных уравнений следующего вида:

i fi = f(tn + сгт,Un + т^ац fj},     i = 1 ...q.

j=1

Видно, что на каждой стадии неизвестное значение fi выражается через уже известные значения и самого себя. Таким образом, система может быть решена последовательным решением q нелинейных уравнений.

Эти методы принято обозначать как DIRK( q, р), где q — число стадий метода, ар — его порядок точности. В русскоязычных статьях можно встретить аббревиатуру ДНРК, однако в настоящей статье будет использоваться англоязычное сокращение, как более распространённое.

В качестве эталонного будет рассматриваться классический метод Рунге - Кутты 4 порядка точности. Это — явный 4-стадийный метод, формулировку которого можно найти в [7]. Методы, которые будут встречаться в данной статье, и некоторые их свойства устойчивости приведены в табл. 1.

Таблица!

Методы интегрирования по времени, которые встретятся в данной работе

Метод	Кол-во стадий (ф	Порядок точности (р)	Устойчивость
DIRK(1, 1)	1	1	А и L
DIRK(1, 2)	1	2	А
DIRK(2, 2)	2	2	А и L
DIRK(3, 4)	3	4	А
RK4	4	4	Условно уст.

Определения А- и L-устойчивости даны, например, в [6]. Под DIRK(1, 1) понимается обратный метод Эйлера — простейшая неявная схема, не требующая дополнительных пояснений. Таблицы Бутчера методов DIRK(2, 2) и DIRK(3, 4) можно найти в [4]. Таблица Бутчера метода DIRK(1, 2) приведена ниже:

1/2

1/2 1

3.    Одномерное уравнение переноса

Одномерное уравнение переноса можно расценивать как простейшую тестовую задачу для численных методов. Как будет видно в следующих разделах, в настоящей работе эта задача оказалась неудачной для анализа методов Рунге - Кутты на диссипативность. Причины этого будут объяснены ниже. Тем не менее в процессе решения этой задачи были сформированы основные идеи способов обработки результатов, что делает полезным представление работы, выполненной в рамках уравнения переноса.

3.1.    Постановка задачи

Рассмотрим линейное уравнение переноса с начальным условием в виде «сглаженной ступеньки» и(х, 0) = (1 + tanh(Hx))/2 и согласованными с ней однородными граничными условиями:

ди ди

+ с — =0, —от < ж < +от, t > 0, dt дх

u(—OT,t) = 0, u(+OT,t) = 1, где с = 1 — скорость переноса.

Для численного решения возьмем границы xl и хд, удалённые на конечное расстояние от начала координат, но достаточно большое для того, чтобы можно было пренебречь их влиянием на численное решение. Пробные запуски показали, что для всех исследуемых методов приемлемой является постановка с границами xl = —256, хд = 512 и интегрированием до момента времени Т = 64. Этот промежуток времени соответствует переносу исследуемых волн на несколько десятков их длин по расчётной области. Обозначим шаг равномерной сетки за h, а шаг по времени т. В расчётах для этой задачи: h = 0.05, шаги по времени соответствуют числам Куранта от 1/8 до 128.

Назовём характерной длиной волны Д расстояние между точками х(и = 0.05) и х(и = 0.95). Начальную длину волны До можно выразить через параметр начального условия Н следующим образом: До = 2/Н • tanh^-1 (0.9). Таким образом, изменяя Н, можно менять До. Будем исследовать волны с начальной длиной от 4 до 48 ячеек сетки. Пример некоторых начальных волн разной длины приведён на рис. 1.

1.2

0.8

0.6

0.4

0.2

А0=4Л

А0=16Л

--------- А0=48Л

-10     -8      -6      -4      -2      0      2      4       6       8      10

Рис. 1. Пример начальных волн различной длины. Единице по оси х соответствует 20 ячеек

Представляет интерес, как интегрирование по времени влияет на длину волны (которая в точном решении сохраняет постоянное значение). Чтобы исключить из сравнения влияние аппроксимации по пространству, решения в конечный момент времени будут сравниваться не с точным, а с эталонным решением, полученным явным методом при очень малом шаге по времени (CFL = 1/8). Аппроксимация по пространству будет одинакова для всех методов. Часто в LES-расчётах конвективные потоки аппроксимируют центральными разностями. Как показала практика, минимальный необходимый порядок точности, при котором эталонный метод в конечный момент времени всё ещё даёт различимый результат для начальных длин волн 4h и более², является шестым. Таким образом,

/ ди\ = Uj +з

\ дх) j

— 9uj +2 + 45uj +i — 45uj— i + 9Uj — 2 — Uj — 3

+ O(h6).

60h

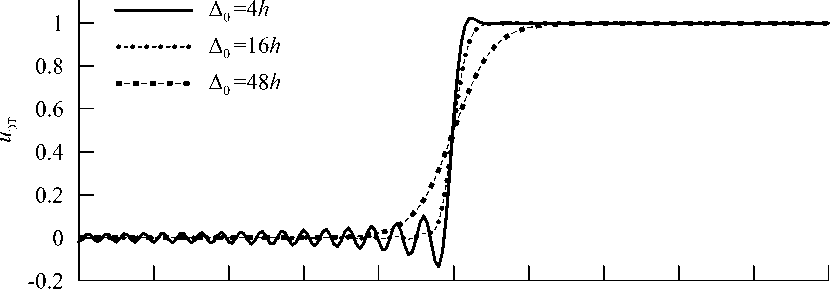
Пример эталонных решений приведён на рис. 2. Видно, что при достаточно малых начальных длинах волн уже на этих решениях присутствуют осцилляции. Повышать диссипа- тивность схемы нельзя, иначе станет невозможным различать решения, соответствующие малым До. Это первый недостаток поставленной задачи для анализа методов в представ ляющих интерес численных постановках.

На рисунке 3 приведены примеры решений, полученных исследуемыми методами. Неявный метод Эйлера сильно «размывает» решение, остальные методы дают решения с осцилляциями. Из-за этих осцилляций становится невозможным определять характерную длину волны по расстоянию между точками х(и = 0.05) и х(и = 0.95). Поэтому будем измерять наклон волны в её центре (и = 0.5) и переводить его в характерный размер волны по следующей формуле:

Д = tanh 1 (0.9)

/ ди \

\^дх "=J

- 1

что соответствует длине исходной во лны с аналогичным углом наклона.

²Имеется в виду следующее. Существует такое число N, что волны начальной длины меньше N «размываются» за время счёта эталонным решением до N ячеек. Таким образом, становится невозможным различать эти решения в конечный момент времени. Чем выше порядок точности пространственной аппроксимации, тем меньше N.

1.2

54     56     58     60     62     64     66     68     70     72     74

Рис. 2. Некоторые эталонные решения в конечный момент времени

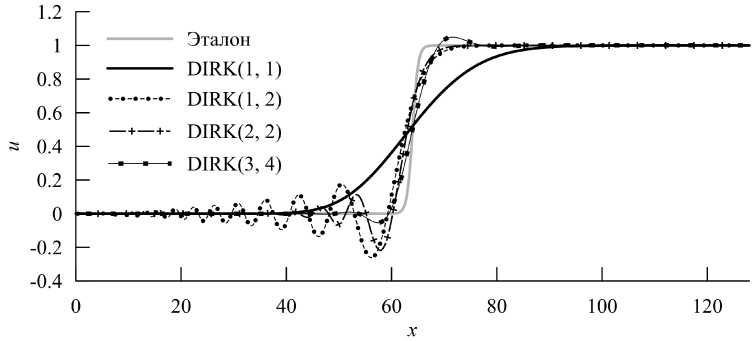
Рис. 3. Решения при CFL = 16, Д0 = 48h

3.2.    Результаты

На рисунке 4 приведены графики сходимости по временному шагу при До = 32h. В легенде после названия метода написан его наблюдаемый порядок точности р, посчитанный по следующей формуле:

_ ln[E(CFLi)/Е(CFL2)] ^р = ln [CFL1 /CFL₂]    ’

где Е (CFL) = ||^ — п_эт||, a CFL1,2 — два наименьших числа Куранта. Все методы, кроме обратного метода Эйлера, выходят на свой теоретический порядок точности.

На рисунке 5 изображены графики эволюции ширины волны со временем для метода DIRK(3, 4) при различных числах Куранта. Видно, что ширина неограниченно растёт, хоть скорость роста её и уменьшается с уменьшением числа Куранта. Это — второй существенный недостаток поставленной задачи: нет возможности однозначно определить, на какую величину выбранные методу «размывают» начальную волну. Она зависит от времени счета, по крайней мере, в случае однородных граничных условий.

Таким образом, в ходе работы с уравнением переноса выявились недостатки этой задачи, которые не позволяют в достаточной мере проанализировать выбранные методы. Во-первых, это — наличие сильных осцилляций даже в эталонном решении, а во-вторых, это — неограниченный рост длины волны со временем. Для частичного решения этих проблем была поставлена другая задача. Её постановка, решение и полученные результаты описаны в следующем разделе.

-1

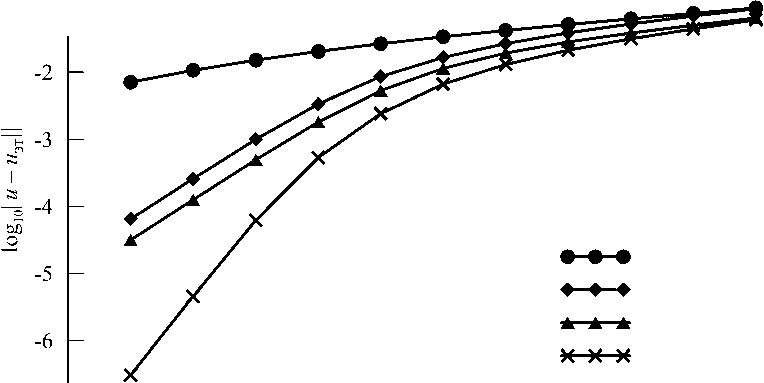
DIRK(1, 1), 0.59 DIRK(1,2), 2.00

DIRK(2, 2), 2.00

DIRK(3, 4), 3.90

-2

-7 L

-4

2 log2(CFL)

Рис. 4. Графики сходимости при △ □ = 32h. В легенде после названия метода указан его порядок точности, посчитанный по двум наименьшим CFL

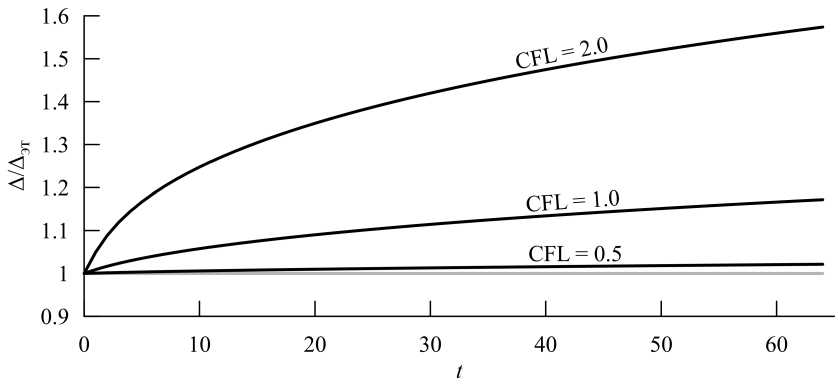
Рис. 5. График эволюции ширины волны со временем для метода DIRK(3, 4). Светлая линия — уровень △ = Дэт

4.    Одномерное уравнение Бюргерса4.1.    Постановка задачи

Запишем уравнение Бюргерса в дивергентной форме:

ди   д / и²

дt   дх 2

-

ди дх

=0,    ^ < х < +^,  t > 0,

u(—^,t) = u_L = 1, u(+^,t) = Ur = 0,

1              ^х

Лх ⁰⁾ = 2 ^{1 - t h}\4;; г

Здесь у — положительное число, которое называется коэффициентом вязкости. Это уравнение можно представлять как одномерное упрощение уравнения Навье - Стокса: оно описывает некоторые его математические свойства. В отличие от уравнения переноса, уравнение

Бюргерса является нелинейным и в нём присутствует механизм «поджатия» волнв!. Под механизмом «поджатия» понимается тот факт, что если обнулить коэффициент вязкости, то, какой бы ни была начальная длина волны, с течением времени область неоднородности будет сжиматься, и через определённый промежуток времени точным решением (6) станет разрыв. Таким образом, при наличии вязкости присутствуют два противоборствующих механизма: один из них, «вязкий», размывает волну, а другой, «конвективный», сжимает. Благодаря этому есть надежда при численном решении уравнения Бюргерса получать решения с длиной волны, которая с течением времени остается ограниченной.

В численной постановке, как и в уравнении переноса, удалим конечные границы xl и xr так, чтобы их влиянием на решение можно было пренебречь. Пробные расчёты показали, что для этого достаточно взять xl = -40 и xr = 600. Пространственную часть будем аппроксимировать центральными разностями второго порядка точности. Этого оказалось достаточно, чтобы в эталонном решении различать волны с разной начальной длиной. Таким образом, в обозначениях метода конечных объёмов d / u2 \ dx 2 /

^Uj +1 / 2 =

U2+1/2

j

Uj + Uj +1

-

2h

u2 ,

--^ + O(h²),

Uj- 1 + Uj ,    ^Uj- 1 / 2 = -----2-----,

d / du \ dx ^dx

Uj- 1

= u—— j

-

■            + O(h2),

где шаг сетки h = 1.

Начальное условие в (6) соответствует стационарному пределу точного решения уравнения Бюргерса при начальном условии-ступеньке. То есть в точном решении фронт волны, не меняясь, будет двигаться вправо с постоянной скоростью, равной 1/2. Пробные расчёты со всеми исследуемыми методами показали, что схожей замечательной особенностью обладают и численные решения. После некоторого переходного периода фронт волны начинает двигаться без изменения своей формы с постоянной скоростью, с высокой точностью равной теоретической. Когда такое установление наступило, решение считается полученным, а дальнейший счёт не имеет смысла. Отметим, что длительность переходного периода (время установления) определяется конкретным методом и начальной длиной волны и никак не влияет на представленные ниже результаты.

Так же, как и в предыдущей главе, введём характерный размер волны Ао, тогда для нового начального условия:

А_о = 8u • tanh^-1(0.9).

Отметим, что, изменяя щ можно менять начальную длину волны в (6). В конечный момент времени будем измерять ширину волны по наклону в центре. Это избавит от проблем, связанных с разнообразностью колебаний решения у разных методов. Однако теперь будем формулу (4) нормировать на амплитуду волны:

А = tanh 1(0.9) (Umax - Umin)

()

где Umax и Umin — максимальное и минимальное значение численного решения соответственно. Это позволит несколько сбалансировать увеличение угла наклона в центре, связанное с появлением колебаний. Поскольку, к сожалению, осцилляции в некоторых численных решениях всё ещё остаются, введём параметр, по которому будет сравниваться степень их проявления. В качестве такого параметра возьмём a = U max — U min.

Будем исследовать длины волн от 2 до 32 ячеек сетки и шаги по времени от 1/4 до 32. При данных параметрах задачи шаг по времени численно равен числу Куранта, посчитанному по начальным данным. В дальнейшем будем синонимично относиться к шагу по времени (At) и числу Куранта (CFL).

Как уже было сказано, все численные решения будут сравниваться с эталонным, полученным классическим методом Рунге - Кутты 4 порядка точности. Предварительные расчёты показали, что достаточно малым шагом по времени является At = 1/16. Примеры некоторых эталонных решений приведены на рис. 6. Видно, что проблема осцилляций эталонного решения при малых длинах волн до конца не решена, из-за чего при обработке результатов могут появиться артефакты, однако существенно ослабленные по сравнению с уравнением переноса.

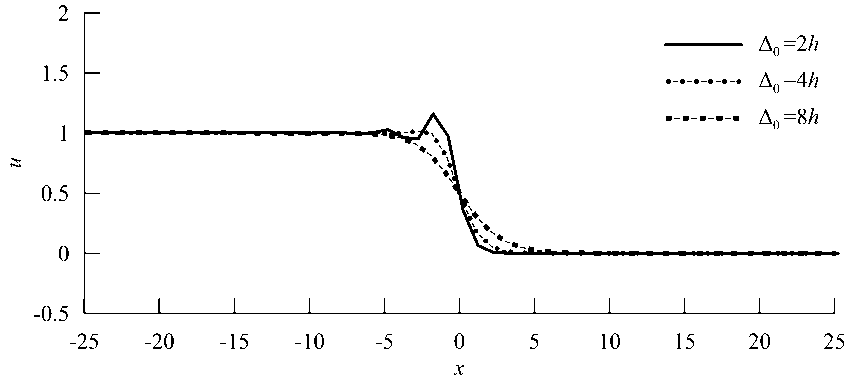
Рис. 6. Некоторые эталонные решения л_эт в конечный момент времени. Единице по оси х соответствует 1 ячейка

Будем называть численное решение приемлемым, если оно «размывает» начальную волну не более чем на 10% по сравнению с эталонным методом и амплитуда его колебаний не более чем на 10% превосходит теоретическое максимальное значение функции, то есть если А/Аэт < 1.1 и а < 1.1.

4.2.    Результаты

На рисунке 7 приведены графики сходимости по временному шагу при Ao = 16h. В легенде после названия метода приведён его порядок точности, посчитанный по формуле (5). Все методы практически достигают своего теоретического порядка точности.

Далее обратим внимание на рис. 8-10. Тут приведены решения в конечный момент времени для различных чисел Куранта при начальной длине волны Ao = 8h. Для удобства сравнения центры волн всех решений помещены в начало координат. Проанализируем полученные результаты. Если число Куранта в два раза меньше, чем начальная длина волны в ячейках сетки (рис. 8), то есть CFL = Ao/ (2h) то решение переносится всеми методами практически одинаково. Выделяющийся результат даёт только обратный метод Эйлера, который сильно «размывает» волну. Никакие из методов не дают заметных осцилляций. Такие решения являются полностью удовлетворительными. Если увеличить число Куранта в два раза (рис. 9), то все методы высокого порядка точности начинают осциллировать, однако решения в большинстве своём остаются приемлемыми. Наименьшие осцилляции даёт метод DIRK(2, 2). Интересно, что, несмотря на больший порядок точности, DIRK(3, 4) порождает колебания большей амплитуды. Вспоминая о свойствах устойчивости исследуемых методов, можно сделать следующее наблюдение: L-устойчивые методы выглядят более предпочтительными для качественного описания переноса волны при больших шагах по времени. Однако это в любом случае не является достаточным условием, так как, например, обратный метод Эйлера также является L-устойчивым, но он слишком сильно диссипирует. Решения при дальнейшем увеличении числа Куранта показаны на рис. 10. Видно, что никакие из этих решений не являются приемлемыми. Обратный метод Эйлера слишком сильно размыл волну, остальные методы породили сильные осцилляции.

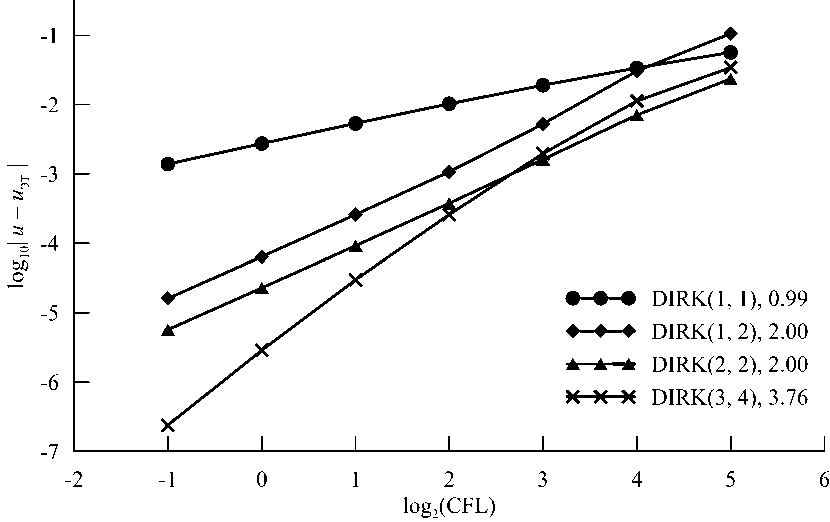
Рис. 7. Графики сходимости при А0 = 16Д. В легенде после названия метода указан его порядок точности, посчитанный по двум наименьшим CFL

1.5

0.5

------- DIRK(1, 1)

---------- DIRK(1,2)

-+-+- DIRK(2,2)

--------- DIRK(3,4)

Эталон

_50    -40    -30    -20    -10     0      10     20     30     40     50

Рис. 8. Примеры решений уравнения Бюргерса в конечный момент времени при А0 = 8Д и CFL = 4

Перейдём теперь к основным результатам. Рассмотрим рис. 11. По оси абсцисс отложен логарифм числа Куранта по основанию 2, а по оси ординат — логарифм по основанию 2 начальной длины волны в ячейках сетки. На самой координатной плоскости изображены изолинии, соответствующие размытию волны ровно на 10% по сравнению с эталоном, то есть изображено сечение графика функции А/АЭT(CFL, А0/Д) плоскостью А/Аэт = 1.1. Эти графики стоит интерпретировать следующим образом: волна заданной начальной длины удовлетворительно переносится тем или иным методом при всех числах Куранта, лежащих левее соответствующей линии. Все линии, параллельные светлой с подписью CFL ^ Ао/Д, соответствуют некоторой линейной зависимости числа Куранта от начальной длины волны. Таким образом, можно сделать следующий вывод: волна переносится удовлетворительно, если CFL < const • Ао/Д, причём константа для обратного метода Эйлера на порядок меньше, чем для остальных исследуемых методов, что говорит о его чрезмерной диссипа- тивности. Отклонение от линейного участка при малых начальных длинах волн обусловлено проявлением ошибок пространственной аппроксимации. Аналогичные графики для степени осцилляций методов приведены на рис. 12. Выводы аналогичны: волны, большие определённой длины, удовлетворительно переносятся при CFL < const • Ao/h. При переносе наименьших волн решения осциллируют неприемлемо сильно, однако эти осцилляции уже связаны с пространственной аппроксимацией. Особенное поведение обратного метода Эйлера можно объяснить тем, что совместно с аппроксимацией по пространству центральными разностями второго порядка точности он осциллирует только лишь при малых длинах волн, когда пространственные ошибки выходят на первый план.

Отметим, что изложенные выше результаты были получены и для других методов: DIRK(2, 3), DIRK(3, 3) и DIRK(4, 3), описание которых можно найти в [4]. Метод DIRK(2, 3) является лишь A-устойчивым и ведёт себя аналогично методу DIRK(3, 4). Другие два метода обладают L-устойчивостью, однако более высокий порядок точности по сравнению с методом DIRK(2, 2) не дал заметного выигрыша.

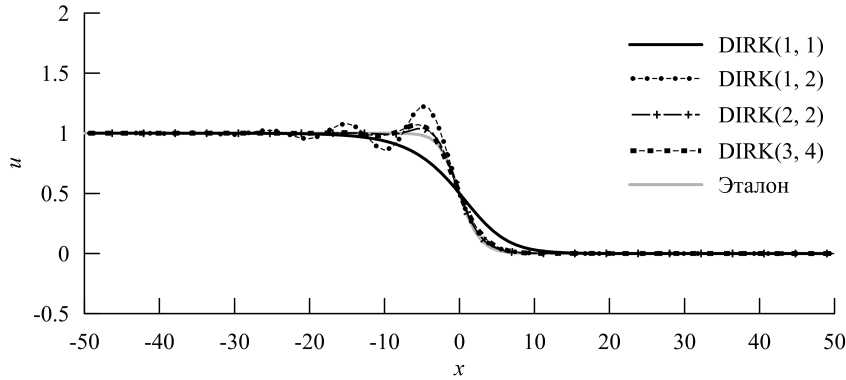
Рис. 9. Примеры решений уравнения Бюргерса в конечный момент времени при A0 = 8h и CFL = 8

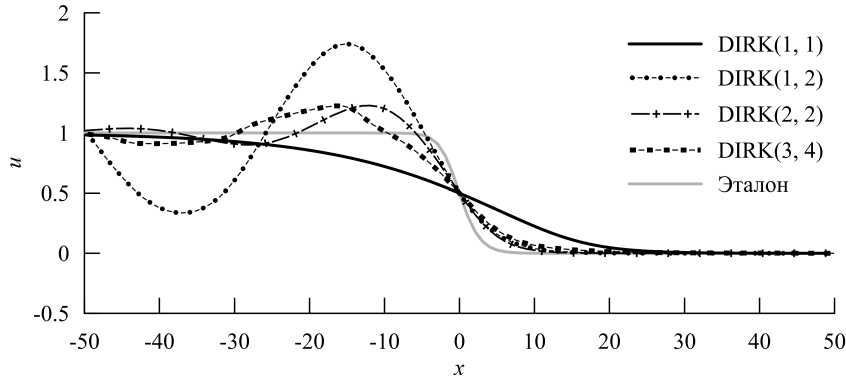
Рис. 10. Примеры решений уравнения Бюргерса в конечный момент времени при Ao = 8h и

CFL = 32

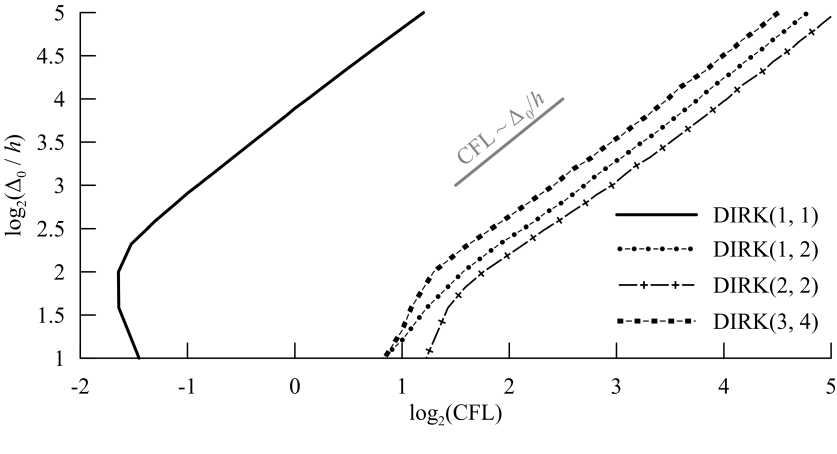
Рис. 11. Изолинии, соответствующие Д/Дэт = 1.1

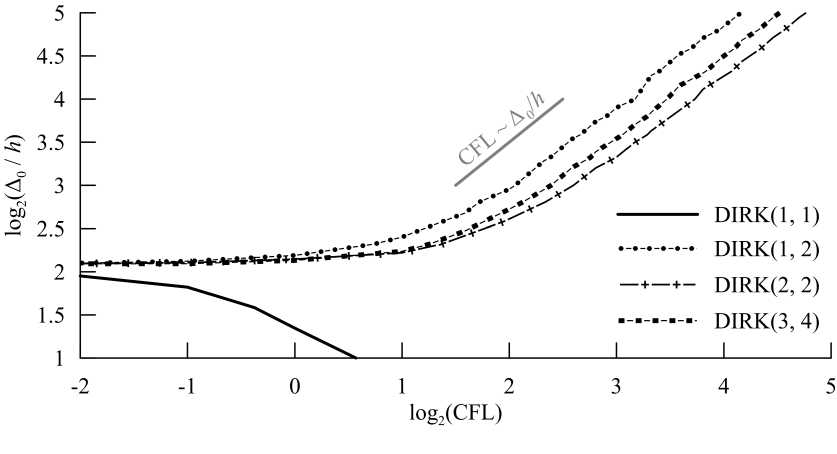
Рис. 12. Изолинии, соответствующие a = 1.1

5.    Заключение

Были исследованы свойства диагонально-неявных методов Рунге - Кутты с использованием одномерных модельных уравнений. Показаны недостатки использования уравнения переноса для сравнения выбранных методов. Эти недостатки были почти полностью устранены переходом к уравнению Бюргерса. Сравнение методов на основе этого уравнения дало следующие результаты. Методы семейства DIRK удовлетворительно, то есть с приемлемым уровнем диссипации и осцилляций, переносят волны длиной До на сетке с шагом h при числах Куранта CFL < const • До/h. Таким образом, если не нужно детально описывать структуру всевозможных волн, а достаточно лишь приемлемым образом описать перенос длинноволновых составляющих решения, то это можно сделать с помощью исследуемых методов при числе Куранта CFL » 1. В гибридных RANS/LES-расчётах турбулентных течений жидкости и газа возникает подобная ситуация [1]. В вихреразрешающих областях течения, где используется подсеточная модель (LES-области), нужно хорошо описывать структуру возмущений, поэтому там число Куранта должно быть меньше или порядка единицы. В пристеночной области пограничного слоя, где действует RANS-модель, сетку нужно сгущать, а значит, условие устойчивости явной схемы будет нарушено. По отношению к RANS-области возмущения из LES-области являются длинноволновыми. Однако в RANS-области детальное описание структуры этих возмущений необязательно. Достаточно лишь описать их перенос без излишней диссипации. Таким образом, использование в гибридных RANS/LES-методах неявных схем (по крайней мере, исследуемых в данной работе) является оправданным. Кроме того, показано, что обратный метод Эйлера, широко используемый для решения стационарных задач, оказывается чрезмерно диссипативным, чтобы быть пригодным для нестационарных расчётов.