Сравнительный анализ генераторов случайных чисел по критерию "Хи-квадрат"
Автор: Шабунин Д.О., Спирин Д.В.
Журнал: Форум молодых ученых @forum-nauka
Статья в выпуске: 11-2 (27), 2018 года.
Бесплатный доступ
Работа посвящена сравнительному анализу генераторов случайных чисел программ: PascalABC.NET, Microsoft Office Excel 2016 и Delphi XE Version 15.0.3953.35171 по критерию «хи-квадрат». Результаты анализа свидетельствуют о пригодности каждого из рассмотренных генераторов случайных чисел, т.е. о соответствии критерию «хи-квадрат».
Генератор случайных чисел, критерий "хи-квадрат", анализ, случайные числа, псевдослучайные числа
Короткий адрес: https://sciup.org/140280443
IDR: 140280443
Текст научной статьи Сравнительный анализ генераторов случайных чисел по критерию "Хи-квадрат"
Случайные числа имеют широкий спектр применения - от моделирования до криптографии [3,6]. Задолго до изобретения компьютеров для решения ряда задач, основанных на случайных числах, ученым приходилось использовать «подручные средства»: вытаскивание шаров из шляпы, карт из колоды или бросание игральных костей. В наше время для решения подобных задач принято выделять три способа получения случайных чисел: таблица случайных чисел, генератор случайных чисел и метод псевдослучайных чисел. Более подробно остановимся на псевдослучайных числах [6].
Числа, которые получаются по какой-либо формуле или имитирующие значения случайной величины X, называются псевдослучайными числами [6]. Под словом «имитирующие», подразумевается, что эти числа удовлетворяют тестам так, словно и были значениями этой случайной величины.
Считается, что первый алгоритм для получения псевдослучайных чисел был разработан Дж. Нейманом. Он называется методом середины квадратов [5].
Затем в 1949 году Д. Г. Лемер предложил линейный конгруэнтный метод [2]. Суть заключается в вычислении последовательности случайных чисел Хп с помощью рекуррентной формулы:
Хп+1 = (а * Хп + с) mod. т. (1)
Еще одним широко распространенным алгоритмом генерации псевдослучайных чисел является алгоритм BBS или генератор с квадратичным остатком. Свое название он получил от фамилий авторов: L. Blum, M. Blum, M. Shub [4].
Заключается он в следующем. Выбираются два простых числа p и q такие, что при делении каждого числа на 4, в результате получается остаток 3. Затем вычисляем целое число Блюма M=p*q. Далее выбирается взаимно простое c M число x и вычисляется стартовое число генератора %0 = %2 mod М. Таким образом, для вычисления i-го элемента используется формула xt = xi-i2 mod М. (2)
В современных компьютерах используется генератор случайных чисел, но что же это такое? Генератор случайных чисел - это программа, дающая на своем выходе последовательность чисел, которая может успешно пройти статистические или вероятностные тесты на случайность [1].
Если говорить о случайных числах, то они должны иметь равномерный закон распределения, это касается и генераторов случайных чисел, иначе их использование может привести к неверным результатам. За одно обращение такой генератор возвращает одно случайное число в установленных границах. Если воспользоваться таким генератором достаточное число раз n , то в идеальном случае в каждую из k категорий попадет одинаковое число и( случайных чисел [6].
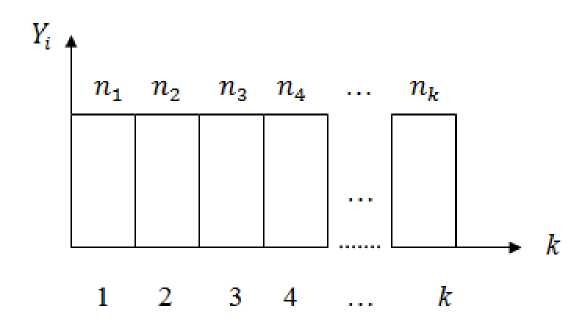
Рис 1.Распределение случайных чисел по категориям k
В нашей работе мы задаемся вопросом: удовлетворяют ли привычные для нас генераторы псевдослучайных чисел требуемому условию? Для решения данного вопроса мы протестируем генератор псевдослучайных чисел в PascalABC.NET, Microsoft Office Excel 2016 и Delphi XE Version 15.0.3953.35171, используя критерий «хи-квадрат» (/2 — критерий).
Этапы анализа
I Подготовительный этап
Пусть у нас есть k категорий, в которые может попасть случайное число. Вычисляется вероятность p i попадания случайного числа в одну из категорий k. Выполняется достаточно большое количество n наблюдений. Находим ожидаемое число np i попаданий случайного числа в одну из категорий k за n итераций [1,3].
|
Категории, k |
0 |
1 |
2 |
3 |
… |
k |
|
Вероятность, pt |
1 /k |
1 /k |
1 /k |
1 /k |
… |
1 /k |
|
Ожидаемое число попаданий, np i |
n/k |
n/k |
n/k |
n/k |
… |
n/k |
Табл. 1.
II Основной этап
Подсчитываем количество попаданий Y^ случайных чисел в каждую из k категорий.
|
Категории, k |
0 |
1 |
2 |
3 |
… |
k |
|
Наблюдаемое число попаданий, Y i |
Y o |
Y i |
Y 2 |
Y 3 |
… |
Yk |
Табл. 2.
Далее перейдем к непосредственному расчету / 2 по формуле
k
х2=Е
I = 1
(Y i - npf>2
npi
III Этап интерпретации результата
После того как произвели все расчеты, сравниваем/2 с числами из таблицы 3 [3] при v= к -1, где v - количество степеней свободы. Если / 2
меньше 1%-й точки или больше 99%-й точки, отбрасываем эти числа как недостаточно случайные. Если χ2 лежит между 1%-й и 5%-й точками или между 95%-й и 99%-й точками, то эти числа «подозрительны»; если χ2лежит между 5%-й и 10%-й точками или 90% и 95% точками, числа можно считать «почти подозрительными». Если χ2 лежит между 5%-й и 95%-й точками то эти числа «пригодные» для использования. Проверка по χ2-критерию часто производится три раза и более с разными данными. Если, по крайней мере, два из трех результатов оказываются подозрительными, то числа рассматриваются как недостаточно случайными [1,3].
|
p=1% |
p=5% |
p=25% |
p=50% |
p=75% |
p=95% |
p=99% |
|
|
ν=1 |
0.00016 |
0.00393 |
0.1015 |
0.4549 |
1.323 |
3.841 |
6.635 |
|
ν=2 |
0.02010 |
0.1026 |
0.5754 |
1.386 |
2.773 |
5.991 |
9.210 |
|
ν=3 |
0.1148 |
0.3518 |
1.213 |
2.366 |
4.108 |
7.815 |
11.34 |
|
ν=4 |
0.2971 |
0.7107 |
1.923 |
3.357 |
5.385 |
9.488 |
13.28 |
|
… |
|||||||
|
ν=9 |
2.088 |
3.325 |
5.899 |
8.343 |
11.39 |
16.92 |
21.67 |
|
ν=50 |
29.71 |
34.76 |
42.94 |
49.33 |
56.33 |
67.50 |
76.15 |
|
ν>30 |
v +^2vX p + 2 xZ p - 2 +O(1/Vv) |
||||||
|
Х р |
-2.33 |
-1.64 |
-0.674 |
0.00 |
0.674 |
1.64 |
233 |
Табл. 3. Некоторые процентные точки χ 2 -РАСПРЕДЕЛЕНИЯ
Производим генерацию случайного числа n=1000 раз и, опираясь на первый и второй этапы, заполняем таблицу полученными данными.
|
Категории, k |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Вероятность, |
0,1 |
0,1 |
0,1 |
0,1 |
0,1 |
0,1 |
0,1 |
0,1 |
0,1 |
0,1 |
|
P i |
||||||||||
|
Ожидаемое число попаданий, n P i |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
|
Наблюдаемое число попаданий, Y i |
94 |
101 |
100 |
95 |
115 |
103 |
86 |
104 |
108 |
94 |
Табл. 4.
Для наглядности распределения поместим полученные значения Y^ в гистограмму.
Количество выпаданий случайного числа от 0 до 9
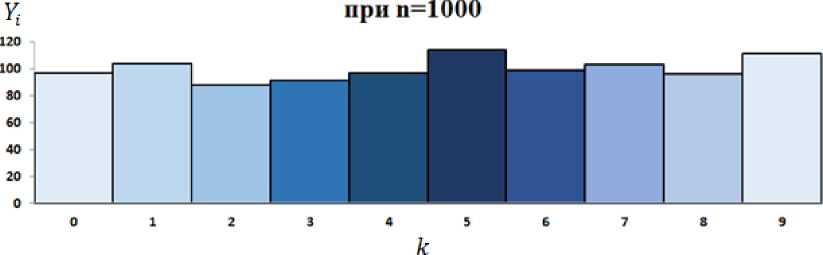
Рис. 2.Распределение случайных чисел по категориям k при n=1000 в
Теперь, когда все данные полученные, найдем значение χ2.
к
^2=Z i=i
(Y i - nP i )2 = (Y 0 - пР о )2 (V.^ + _ + (Y 9 - ПР 9 )2
HP i
пр о
пр1
пр9
= (94 - 100)2 (Y1 - 100)2 (Y9 - 100)2 =
100 100 ^ 100 ■ ■
Полученное нами значение χ 2 =6,08 сравниваем с данными таблицы
1 при ν = 9. Несложно заметить, что экспериментальное значение лежит между 25%-й и 50%-й точками, что говорит о «пригодности» полученных случайных чисел.
Остальные опыты проводятся аналогично.
В ходе исследования были получены следующие результаты
|
Среда |
n |
k |
Результат ( x 2 ) |
|||
|
1 опыт |
2 опыт |
3 опыт |
СРЕДНЕЕ |
|||
|
PascalABC.NET |
1000 |
10 |
3,92 |
6,08 |
9,58 |
8,47 |
|
5000 |
10 |
10,4 |
4,65 |
3,92 |
6,32 |
|
|
10000 |
10 |
13,4 |
7,36 |
7,71 |
9,49 |
|
|
Microsoft Office Excel 2016 |
1000 |
10 |
3,92 |
5,04 |
10,9 |
6,62 |
|
5000 |
10 |
11,3 |
7 |
6,07 |
8,124 |
|
|
10000 |
10 |
5,45 |
14,3 |
11 |
10,25 |
|
|
Delphi XE Version 15.0.3953.35171 |
1000 |
10 |
4,74 |
6,8 |
7,08 |
6,21 |
|
5000 |
10 |
9,62 |
7,22 |
7,28 |
8,04 |
|
|
10000 |
10 |
8,75 |
8,72 |
4,48 |
7,32 |
|
Табл. 5.
Вывод
В ходе работы были проверены три генератора псевдослучайных чисел в трех средах: PascalABC.NET, Microsoft Office Excel 2016 и Delphi XE Version 15.0.3953.35171 при помощи критерия «хи-квадрат» (χ2 – критерий). Сравнительный анализ показал, что каждый из генераторов псевдослучайных чисел дает пользователю последовательность случайных чисел, пригодную для использования, удовлетворяющую χ2 –критерию. В дальнейшем планируется увеличить количество опытов, а также расширить круг программ, которые будут проверены.
Список литературы Сравнительный анализ генераторов случайных чисел по критерию "Хи-квадрат"
- Бакнелл, Д. Фундаментальные алгоритмы и структуры данных в Delphi - М.: ДиаСофтЮП, 2003. - 557 с.
- Баркалов, К.А. Образовательный комплекс «Параллельные численные методы» - Н. Новгород: ННГУ им. Н.И. Лобачевского, 2011. - 27 с.
- Кнут, Д. Искусство программирования. Том 2. Получисленные алгоритмы - М.: Вильямс, 2007. - 788 с.
- Краснов, М. В.методические указания «Математические методы защиты информации». Ч. 3 - Ярославль: ЯрГУ, 2013. - 48 с.
- Муравьев, Г.Л. Имитация случайных объектов - Брест: БрГТУ, 2011. - 33 с.
- Соболь, И. М. Метод Монте-Карло - М.: Наука, 1968. - 64 с.


