Сравнительный анализ методик оценки количественных характеристик шероховатости наноразмерных структур

Постоянное развитие технологий изготовления КМОП интегральных микросхем выражается в масштабировании всех линейных размеров транзисторов[1].Вто же время статистический разброс значений критических размеров структур не масштабируется [2]. Такая тенденция ведет к постепенному усилению влияния негативных эффектов, связанных с статистическим разбросом, и, начиная с некоторого размерного порога, такие эффекты более недопустимо игнорировать. Теоретически и экспериментально установлено, что такой границей следует считать технологическую норму «90 нм»,

«Московский физико-технический институт (государственный университет)», 2018

ниже которой упомянутые размерные эффекты приводят к существенной деградации характеристик приборов и ухудшению их воспроизводимости по кристаллу [3]. В частности, неровноств краев затвора МОПТ ведет к разбросу порогового напряжения транзисторов [4, 5], что вступает в противоречие с требованиями на постоянное снижение уровня порогового напряжения и неизбежно будет являтвся одним из главных ограничителей масштабирования кремниевой технологии микроэлектроники.

Для того, чтобы контролировать неровность краёв топологических элементов интегральных микросхем, в первую очередь необходимо адекватно давать количественную оценку величины неровности. На данный момент известно несколько способов количественной оценки показателей шероховатости наноразмерных структур. Помимо традиционного способа вычисления среднеквадратичного отклонения используются методы, учитывающие пространственную периодичность отклонений краевых точек топологического элемента. Между тем, флуктуационная картина распределения периода неровности края линии на расстояниях, превышающих размер исследуемых кадров, может сильно искажать результаты измерений. Однако в литературе отсутствуют сведения экспериментального характера о справедливости оценки пространственной периодичности, определяемой такими методиками, и как следствие - всех остальных параметров моделей.

Данная работа не ставит перед собой цели подвергнуть сомнению принципиальную применимость упомянутых методов, но предпринимается попытка анализа достоверности результатов, полученных наиболее распространёнными способами определения количественных характеристик шероховатости наноразмерных структур.

2.    Параметры шероховатости и методики их оценки

Безусловно, морфология всей боковой поверхности топологических элементов определяет спектр электрофизических параметров будущих устройств. Однако применительно к технологии производства интегральных схем появление структурированных объектов в топологических слоях есть результат процессов плазма-химического травления. А в таком случае геометрия маски полностью переносится вглубь нижележащего слоя/подложки в направлении травления материала [6]. Это означает, что картина неровности края в любом плоскопараллельном срезе структур будет идентичной и, следовательно, для анализа шероховатости боковой поверхности структур достаточно лишь рассмотрения распределения отклонения боковых точек края топологического элемента в любой плоскости.

Количественным показателем отклонений краевых точек топологического элемента традиционно служат величина неровности края (LER) и неравномерности ширины (LWR) линии, определяемые по аналогии с правилом трёх сигм:

п

LERk = 3

Е (^жгк — $к )2 г=1

п

где к = 1, 2 — правый или левый края линии.

Для всей линии неровность края вычисляется по формуле:

LER =

ILER1 + LER2²

V------2------

Однако применяются и другие параметры, учитывающие, в отличие от LER и LWR, пространственное распределение отклонений краевых точек элементов. К наиболее популярным методикам оценки количественных характеристик шероховатости следует отнести анализ спектральной плотности мощности и исследование функции корреляции.

2.1.    Анализ корреляционной функции

Данный метод исследования шероховатости структур основывается на исследовании корреляции отклонений точек от прямой, аппроксимирующей край. Соотношения данных отклонений численно описываются высотно-высотной корреляционной функцией G (r), заданной на расстояниях r = md, где d — период краевых точек:

.. N—т

G(md) =

£ (Ф+т - й)², N — m ^^

i=1

где di = Xi — ж — поперечные отклонения краевых точек линии.

Данная функция связана с нормализованной автокорреляционной функцией

......              _ВД = 1 — GM.                   .

2сг2

где r = md — расстояния, кратные периоду краевых точек, с — среднеквадратичное отклонение точек от линейной регрессии края.

Начиная с некоторого расстояния (т.н. длина корреляции) между точками края корреляция их отклонения исчезает, т.е. автокорреляционная функция R(r) стремится к нулю, а значит, функция G(r) устанавливается на некотором постоянном уровне. Из соотношения (2) следует связь установившегося уровня вычисляемой функции G(r) и среднеквадратичного отклонения и, равного, по определению (1), 1/3 величины LER.

2.2.    Анализ спектральной плотности мощности

Периодичность структур оценивается также с помощью диаграммы спектральной плотности мощности (PSD), отображающей амплитуды компонент преобразования Фурье отклонений точек края исходной линии. Данный способ нахождения величины LER состоит в анализе горизонтальной части диаграммы спектральной плотности мощности в зоне низких пространственных частот. Связь с и, пропорциональной, по формуле (1), величине LER, следует из теоремы Парсеваля:

с2 = 2^ j р(k)dk, где Р(k) = ^ J у(х)е ik'xdx — преобразование Фурье линии края.

3.    Объект и методика исследования

Объектом исследования выступает плотная периодическая решётка Si плавников, являющаяся базовой структурой на пути формирования FinFET. Изображение структур в поперечном сечении представлено на рис. 1. Снимки структур в виде сверху, подлежащие количественному анализу, были получены на растровом электронном микроскопе (РЭМ) Hitachi CG4000, имеющего разрешение 1,8 нм. Номинальная ширина плавников составляет 30 нм, а период — 200 нм. Количественные характеристики шероховатости структур рассчитывались с помощью методик, предложенных в [7]: по определению, по уровню насыщения функции корреляции отклонений от линейной аппроксимации координаты края линии и по уровню графика спектральной плотности мощности в зоне низких пространственных частот.

В основе анализа достоверности результатов измерений лежит справедливое предположение об однородности воздействий технологических процессов формирования исследуемых структур в малой выделенной области кристалла (или пластины). В таком случае сильное изменение количественных показателей шероховатости (например, LER) на различных кадрах обозначенной области кристалла будет свидетельствовать о неточности результатов статистического анализа.

Для оценки стабильности определения величины LER, измеряющейся по одной и той же методике на серии кадров, используется безразмерный коэффициент вариации. Он характеризует относительный разброс полученной серии измерений величины:

^"ТЕД

k )

(LER') ’

I Е (^LE«_I-(^LE«))²

где k^LER) = \ л 2ER = V -------N------- дисперсия величины LER.

Рис. 1. РЭМ-изображепие исследуемой решётки Si плавников в поперечном сечении

В силу того, что исходные величины LER являются масштабно независимыми, рассматриваемый индикатор стабильности также является масштабно независимым, что позволяет использовать его как единую характеристику качества результата отдельного метода.

4.    Результаты исследования и обсуждение

В режиме пакетной обработки изображений проанализированы 22 кадра экспериментальных структур в окрестности 100 мкм центральной области пластины. На каждом изображении выделялись линии поперечных максимумов для двух краёв каждой из линий, попавших на кадр (рис. 2). Фактически это соответствует максимумам интенсивностей электронной эмиссии поверхности, которые затем интерпретировались как структуры, подобные искомым краям. Примеры обработки одиночных кадров методами анализа корреляционной функции и спектральной плотности мощности представлены на рис. 3 и 4.

Важно отметить, что в ряде случаев оценка выбранных величин методом анализа спектральной плотности мощности представляется затруднительной в силу невозможности однозначного выявления линейного участка в зоне высоких пространственных частот. Кроме того, к недостаткам данного метода следует отнести и тот факт, что теорема Парсеваля, позволяющая получить значение количественного параметра, связанного с шероховатостью, включает интеграл приведённой функции спектральной плотности мощности (5). Его значение явным образом зависит от дискретизации преобразования Фурье, а значит, от разрешения использовавшихся кадров. Таким образом, при разных условиях получения кадров на одних и тех же объектах будут получаться различные значения LER.

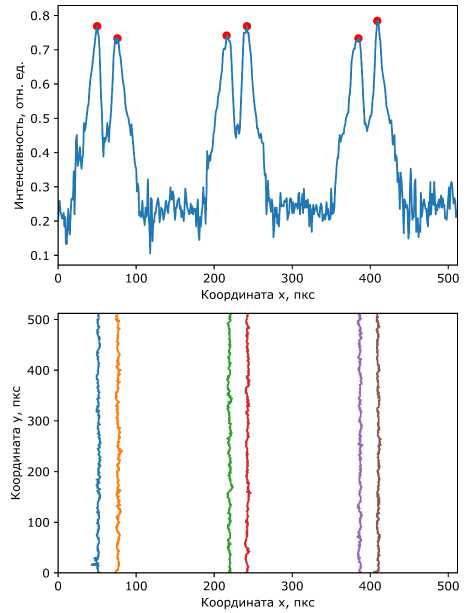
Рис. 2. Детектирование линий с изображения решётки плавников

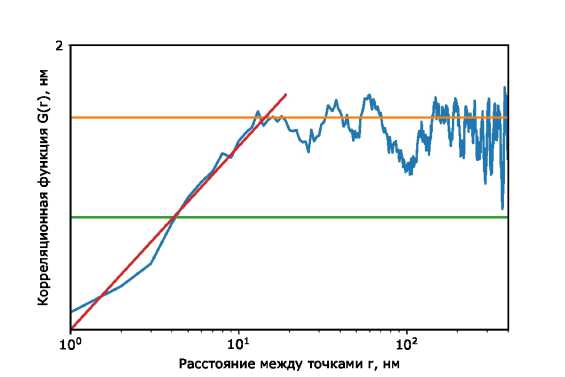
Рис. 3. Результат обработки одного кадра методом анализа корреляционной функции: Д2 ст = 1, 69 им, длина корреляции £ = 4 им, LER = 3, 59 нм

Основные результаты исследования представлены в табл. 1.

Сравнивая абсолютные значения LER, полученные тремя способами, выявлено, что результат измерения существенно зависит от использованной методики. Итоги вычислений величины неровности края по функции спектральной плотности мощности выбиваются из ряда данных других методов, а значит, в приведённой реализации, особенности которой упомянуты выше, данный метод не применим, по крайней мере, при исследовании базовых структур ҒіпҒЕТ-технологии.

Анализ полученных результатов подтверждает предположения, высказанные в [9], о том, что исследование частотного распределения спектра шероховатости целесообразно проводить для определения причин, вносящих вклад в величину шероховатости. Однако коэффициент вариации величины LER, оценённой с использованием данных методов, оказывается больше в 1,3-1,5 раза в сравнении с расчётом по формуле (1). Наилучший показатель вариации выявлен для методики определения величины неровности края по среднеквадратичному отклонению и составляет 0,047.

Таким образом, результаты показывают, что наилучшая стабильность результата достигается при определении величины линейной шероховатости по определению, т.е. по формуле (1).

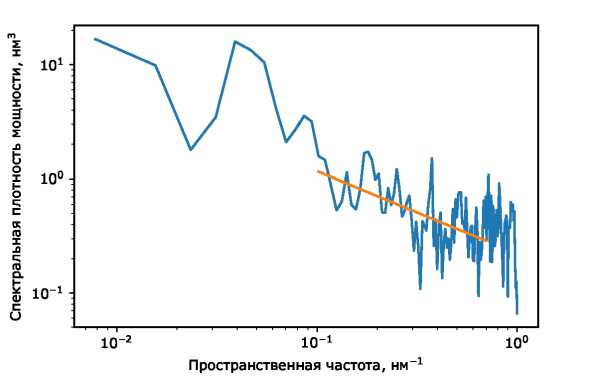
Рис. 4. Результат обработки одного кадра методом анализа спектральной плотности мощности: длина корреляции £ = 1,43 нм, LER = 1, 55 нм

Таблица!

Результаты измерений неровности края (LER) и её воспроизводимости в малой окрестности кристалла

Метод	формула по определению	корреляционная функция	PSD
^LER^ нм	4,193	4,431	1,655
Дисперсия LER, нм2	0,039	0,169	0,020
Коэффициент вариации	0,047	0,092	0,085

5.    Заключение

В работе проведен сравнительный анализ наиболее популярных методик оценки количественных характеристик шероховатости наноразмерных структур с точки зрения воспроизводимости результатов измерений. Воспроизводимость результатов определения LER оценивается с помощью коэффициента вариации значений в соответствии с предложенной в данной работе методикой. Обнаружено, что наилучшая стабильность достигается при определении величины неровности края по среднеквадратичному отклонению. В связи с чем именно данный метод рекомендуется использовать в целях производственного контроля шероховатости топологии приборных кристаллов.