Сравнительный анализ методик расчёта центробежных насосов в приложении к малоразмерным конструкциям авиакосмического назначения

Малоразмерные центробежные насосы (МЦН) с диаметром рабочего колеса (РК) D 2 ≤50 10^-3 широко применяются в авиационных и космических системах подачи топлива, балансировки центра тяжести, впрыска воды в воздушные каналы двигателя, охлаждения локатора, терморегулирования, дозаправки в воздухе. В состав энергетического комплекса одного самолёта или орбитальной станции могут входить десятки МЦН. Проектирование МЦН базируется на тех же, что и для полноразмерных центробежных насосов (ЦН) методических подходах. Однако набор функциональных зависимостей и рекомендуемый диапазон значений в практике проектирования ЦН очень ш и рок. При этом расчет коэффициента напора Н , гидравлического кпд η г , гидравлического параметра k z η г многовариантен, что обусловливает необходимость проведения сравнительного анализа методик расчета и оценки их пригодности к проектированию МЦН.

Эффективность рабочего процесса в центробежном насосе кроме коэффициента полезного де йс твия оценивается и коэффициентом напора Н = k z q , (1 - q_р), где п г - гидравлический кпд, а k z - коэффициент, учитывающий влияние конечного числа лопаток РК на напор, q p - расходный параметр.

Гидравлический кпд ЦН η г оценивает суммарные гидравлические потери L г = L под + L рк + L отв , состоящие из потерь в подводе L под , рабочем колесе L рк , отводе L отв и определяется по формуле: п г =1 — L_r/H_T, где Н_т - теоретический напор насоса.

Оценка гидравлических потерь в центробежном насосе производится путём анализа связи

между L г и геометрией рабочего колеса. Выбор значимого геометрического параметра РК, абсолютн о го или относительного (например, D 1пр или D₁ ) при этом зависит от класса ЦН, области его применения и сложившихся подходов в оценке гидравлического совершенства проточной части.

Распространенными формулами вычисления значений η г полноразмерных центробежных насосов являются:

- общепромышленные [1, 2]:

П г = 1 —

0.42

( lgD_bp - 0.172 ) 2

- погружные [2]:

П г = 1 —

0.55

V

_& ^lgR?

V

• 10 3

V

Л 2

+ 0.408

V ■

;

- насосы ЖРД [3]:

П _г = 0.82 - 10(D - 0.65)² при 0,55-0,65 < D 1 <

0.8;                                       (3)

П = 0.83 - 50(D , - 0.7) 3 при D 1 >  0.7;   (4)

- высокооборотные [4]:

П г =

0.88 - 0.91 • D 1

1^

Поле значений функции η г пр =f(D 1пр ), характерных для общепромышленных насосов при n=6000 об/мин, изображено на рис. 1. Здесь приведенное значение гидравлического кпд η г равно отношению η г из формул (1), (2) к средневзвешенному значению η г для общепромышленных насосов [5].

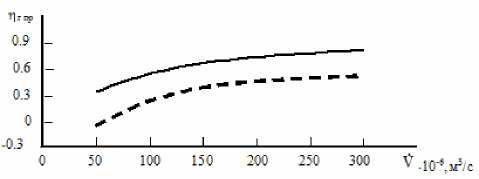
Рис. 1. Оценка гидравлического КПД МЦН с использованием методик для полноразмерных насосов: сплошная линия – центробежные и осевые насосы; пунктирная – погружные центробежные насосы для скважин

Попытка применения формул расчёта η г , предназначенных для других классов ЦН, к режимам работы МЦН приводит к следующим результатам.

В зависимости от объёмного расхода рабочего тела:

П г =-0,05-0,95 при V =50 - 10 -6 м 3 /с,

П г =-0,42-0,95 при V =300 - 10 " ⁶ м³/с.

В зависимости от относительного диаметра _{D 1} : η г =0,51-0,85 при D 1 =0,55

η г =-0,23-0,78 при D 1 =0,8.

Полученные результаты указывают на существенное различие величин η г , при этом по адаптированным к МЦН авиакосмического назначения методикам [7, 9] необходимо задавать величину η г =0,8-0,85 или вычислять по формуле:

= 1 -

Л'"    (igDinp — 0.172)2 , где

D1np = 4.25 -3 V -103, мм n             .(6)

На основе накопленной статистики авторы [7, 9] для МЦН космических аппаратов предложили формулу расчёта гидравлического кпд как функцию коэффициента быстроходности η г =0,38 n s ^0,21. Эта зависимость, представленная на рис. 2 показывает, что в зоне n_s=20-40, в которой энергетически более эффективными являются вихревые и дисковые насосы, кпд МЦН должно достигать значения η г =0,71-0,82. Это не соответствуют представлениям о гидродинамике тихоходных лопаточных машин, устанавливающих для центробежных насосов нижнее значение n s =40, обеспечивающее приемлемый уровень кпд.

С учётом известных значений составляющих полного кпд: расходного η р , дискового η д и механического η м значение η г при n s =70 у МЦН не превысит уровня η г =0,85, в то время, как по данным рис. 2 гидравлический кпд МЦН должен составлять не менее η г =0,95.

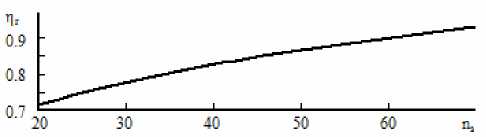
Рис. 2. Зависимость коэффициента η г от n s

Большой разброс данных по различным методикам [4, 7, 8, 9, 11] отмечается и при оценке k z Расчётные формулы определения коэффициента k z по-разному учитывают влияние конечного числа лопаток на величину теоретического напора для насосов:

- ЖРД kz

0.66 - 10(D 1 - 0.7)²

0.8³ - ⁵0(D 1 - 0.7) 3 _Пр_И D > 0.07;

- высокооборотных

0.7 - 0.73 - D 1

0.88 - 0.91 - D 1 . ^;

- космических аппаратов

, 1.1 + 1.2 - sin В

1 + ^2л z - (1 - D 1² )

к . = 0.832 <”, _Где P 2_л в _рад._{; (W})

одноярусная решётка РК k = 1.1 + 1.2 - Sin р2л z z - (1 - D12)

, двухъярусная решётка РК k =      1.1 + 1.2 - Sin в2л

. . дл - (1 - D 2 ) + Z k - (1 - D 2 )

- авиационных z - (1 - D12)     _

• 1.2 - (1 + sin р _2л) + z - (1 - D 1 ²)

Графики на рис. 3, построенные по указанным зависимостям, отличаются как количеством переменных, так и характером изменения k z . Аналогичная картина наблюдается и при оценке коэффициента напора Н:

• - для насосов ЖРД

0.7 - 0.73 - D 1 н =                  - ( 1 - q₽ ) 0.88 - 0.91 - D 1 ^P/

;

- для МЦН космических аппаратов:

Н = (0.65...0.7) - ( 1 - q р )

,

Н = 0.72 - 0.22 - 10 — 3 - n s

Графическая зависимость по формуле (15) изображена на рис. 4. По одним данным на режимах работы МЦН диапазон измене ни я коэффициента нап о ра составляет Н =0,63-0,7, а по другим Н =0,5-0,63, пр и чём характер монотонности изменения Н для МЦН соответствует показателям высокооборотных насосов.

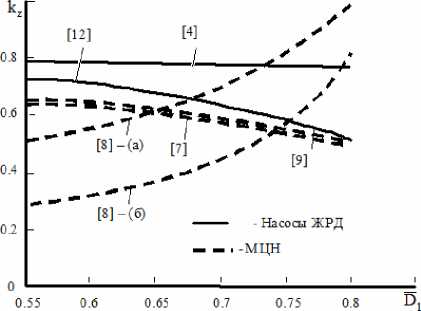
Рис. 3. Оценка коэффициента k _z : а – одноярусная решётка РК; б – двухъярусная решётка РК

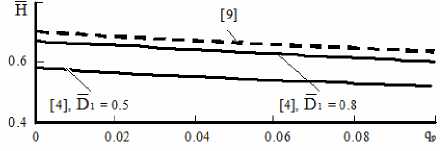
Рис. 4. з ависимость коэффициента напора Н от расходного параметра q р : пунктир – малоразмерные центробежные насосы, сплошная линия – высокооборотные центробежные насосы

Выводы: так как расчётные формулы в насосостроении часто базируются на систематизации эмпирических данных, относящихся к узкому диапазону режимных и геометрических параметров, расширение области их применения возможно на основе введения поправочных коэффициентов, получаемых путём обобщения опытных данных. В практике проектирования МЦН наиболее эффективно применять многофакторные математические модели энергетических параметров, полученные на основе статистической обработки экспериментальных данных с целью получения эмпирических коэффициентов, уточняющих универсальные функциональные зависимости.