Сравнительный анализ методов адаптации параметров регулятора системы управления робота-манипулятора

Цель данной статьи – выбор эффективной системы управления манипулятором, основанной на адаптивном ПИД-регуляторе. Робот-манипулятор есть нелинейная динамическая система, и для его управления часто используют методы, основанные на линеаризации обратной связи [1]. Для эффективного управления необходимо знать точные динамические характеристики манипулятора, такие как, например, тензоры инерции звеньев при переменной нагрузке и коэффициенты трения в сочленениях. В реальной практике определение значений этих характеристик крайне трудозатратный процесс. Их влияние соответствует дрейфу параметров объекта управления. Один из подходов адаптивного управления подобными системами является ПИД-регулятор с настройкой параметров в реальном масштабе времени. Настройка регулятора может производиться нейронной сетью [2, 3] , нечеткой логикой [4], нейро-нечеткой сетью [5].

В данной статье разработана процедура адаптации параметров регулятора на основе симплексного инвариантного метода [6], приведены результаты моделирования и сравнение с другими системами управления манипуляторами, основанными на ПИД-регуляторе.

Методы ада пт-ации

В общем случае динамика n -звенного манипулятора описывается нелинейным уравнением

T (t ) = M ( q ( t )) • q ( t ) + V ( q ( t ), q ( t )) + G ( q ( t )) + F ( q ( t )),             (1)

⁾ где T (t ) - вектор) nx 1 моментов в сочленениях, Нм, q ( t ) - вектор nx1 угл овых ко ординат в сочленениях, рад; M ( q ( t )) - матрица nxn инерций звеньев манипулятора; V ( q ( t ), q ( t )) - вектор nx 1 кориолисовых и центробежных сил; G ( q ( t )) - вектор nxl гравитационных сил; F ( q ( t )) - вектор n× 1 сил трения в сочленениях.

Параметры уравнения (1) зависят от многих неконтролируемых возмущений, например тензоры инерции звеньев при переменной нагрузке и коэффициенты трения в сочленениях, а следовательно, изменяются во времени с различной интенсивностью. В этой связи разработаны различные подходы адаптации параметров системы управления манипулятором [2-5].

Рассмотрим непрерывную сис тем у управлен ия на о снове классического ПИД-регулятора (рис. 1).

ПИД-регулятор реал изует упра вление

t

т ⁽ t ) = ( К , 0 . Л К p ( t )) ■ е ( t ) + ( К i 0 +л ^к i ( t ) )J е ( t ) d . К d , + ЛК , ( t ) )-d>. (2)

где K _р0 , К _i0 , K _d0 - векторы nx 1 про порциональных, интегральных и дифференциальных ко -^эффи^{циентов} регул^{ятора соответственно;} А К ⁽ t ) _р , ^АК ,. t ), А ^К d^{( t} ) ^- векторы nx 1 ^приращ™ ^коэффициентов регулятора; e (t ) = ( q _d ( t ) - q ( t )) - вектор nx 1 ошибки слежения, рад; q _d ( t ) - вектор nx l за данных значений угловых координат, рад; q ( t ) - век тор nx1 текущих значений углов ых координа^т, рад; q ⁽ t ) ^- измеренный ве ктор n^x 1 значений скоростей, рад /с.

Адапт ац ия параме тров р егул ятора ре али з уе тся в со отве тс твии с кри терием (ц еле во й -Л функцией)

Q ( t ) = ¹ е ² ( t ) ^ min ,                                               ⁽³⁾

2           ЛК( t )еК где К = {Л К (t): Л- К (t) е E 3, Л К т1п < Л К (t) < Л К max}.

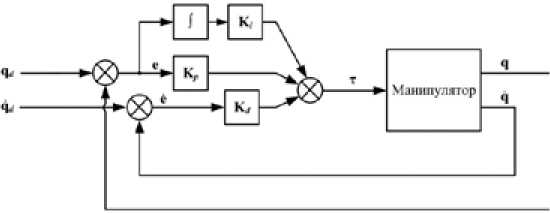
Р ис. 1. Структурная с хема не прерывной систем ы управлен ия манипулято^ром на основе класс ичес кого ПИД-регулятора без адаптации (ПИД)

Первая схема адаптации предусматривает коррекцию векторов приращений коэффициен тов регулятора относительно векторов базовых значений коэффициентов Kp0, K/0, Kd0 (рис. 2).

При настройке регулятора нейронной сетью ПИД-регулятор представляет собой однослойную нейронную сеть (рис. 3).

В качестве адаптера испо льзуется а лгоритм об ^ ратного распростр анения о ши бки на основе градиен тного м етод а [3].

Настройка п араметров р егулятора п рои сходит по в ыражению d Qj Kpj (t) = Kpj о + npj ' J о dKpj

' , d Q

Кц(t) = Кцо + n -J   Ldt, о dKij

K4j(. t) = Kdjo + ndj‘j,

0 d d j = 1, n -номер сочленения,

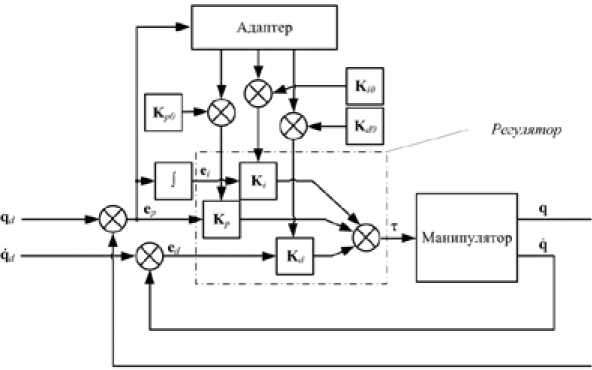
Р ис. 2 . Структурна я схема ад апти вной систем ы управлен и я с настройкой п а ^ ра_^метров ПИД-ре г улятор а нейронной сетью (ПИД-НС)

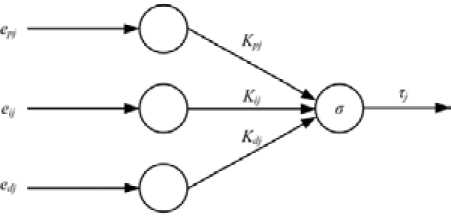
Р ис. 3. Структ^ура нейронно й сет и ПИД-регулятора где npj, nj, Пdj — векторы их1 скоростей обучения пропорциональной, интегральной и дифференциальной с оставляю щих для j-го с очленения соот ве тственно.

Данный алгоритм является нелинейным и способен обучаться во время работы. Рассмотрим в озм ожн ость испол ьз овани я в качест ве адаптера метод п оис ковой о п тимиз аци и. Целев ая функция (3) зависит от времени, и закон её изменения априори неизвестен. Большинство методов оптимизации неэффективны в условиях дрейфа целевой функции, а при определенных скоростях дрейфа и неустойчивы. Если в качестве контролируемого возмущения использовать время проведения эксперимента в текущей точке, то можно применить симплексный инвариантный метод (СИМ) [6].

Процесс поиска СИМ реализуется в дискретные моменты времени t k = к • T ₀ , где Т ₀ - интервал дискретизации; к - шаг поиска (дискретное время). На интервале Т ₀ происходит вычисление целевой функции и принятие решения о направлении поиска в пространстве приращений A K .

Обобщенно алгоритм метода:

• 1)    на к -м шаге поиска вытчисляется целевая функция Q ( к ) и фиксируется время её вычисления z ( к ). Предполагается, что время измерения невязки e ( к ) и функции Q ( к ) совпадают;

• 2)    аппроксимируем на ^к -м шаге ^целевую функцию Q ^{( к} ) выражением

Q (к ) = a T х,(5)

рассчи тываетс^я текущ а^я оценк а д рейфа ц елевой ф ункции рекурр ен тным м етодом н аименьш их ква дратов;

a(k) = a(k -1) +     тСk -1), X( k)     [Q(k) - aT (k -1) • x(k)],(6)

1 + x' (k)• C(k-1)• x(k)LJ где x(к) = (AKp (к) A Ki (к) AKd (к) Az (к))T - составной век тор воздействий; a( к) = (a 1( к) а 2(к) а 3(к)) T -составной вектор оценок целевой функции на к-м шаге поиска; ai(к) - оценки зависимости целевой функции от приращений параметров регулятора на к-м шаге поиска; b(к) - текущая оцепка дрейфа целевой функции; C(к-1)- ковариационная матрица оценок.

В области экстремума целевой функции оценки a 1 ( к ), а ₂ ( к ), а ₃ ( к ) близки к нулю. Это является при зна ком дости жения о бласти э кстремум а;

• 3)    вычитание влияния дрейфа на значение целевой функции в вершинах текущего симплекса

Q j ( k ) = Q * — b (к ) '^А Z j ,j = 1,..., m + 1, J * s ;                                      ⁽⁷⁾

• 4)    принятие решения о направлени!и поиска, а именно отражение худшей точки (вершин ы, имеющей макс и мальное значение Q j ( k ));

• 5)    переход к пункту 1.

Эффективность алгоритма зависит от длины ребра симплекса (приращения K p , K i , K d ), скорости дрейфа, уровня помех, а 'также от процедур адаптации парамет ров и стратегии поиска.

Вторая схема адаптации предполагает непосредственное воздействие на формируемое управление вектором 1моментов T ( t ) в сочленениях. Структурная схема такой адаптивной САУ с исп ользов анием нейр онной сети п рив едена на р ис. 4 [ 7].

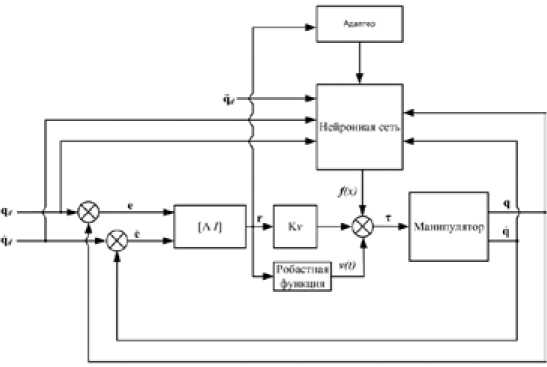
Р ис . 4. Схем а адаптивной С ^ АУ с ко рректировкой векто ра момент ов τ нейронн ой сетью (АдСА ^ У-НС)

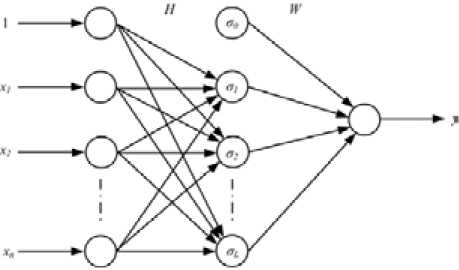
Рис. 5. Струк тура нейронн ой сет и

Структура нейронной с ети и зображена на рис. 5.

Управление рассчитывается по формуле:

e ( t ) = q ( t ) _d - q ( t ),

^{r (} t ) ^{e ( t} ) ^{+ Л е (} t )                                                                  ⁽⁸⁾

τ(t) = f (x(t)) + Kv⋅ r(t) - v(t), где q(t) - вектор nxl, рад; e(t) - вектор ошибки nxl, рад; Л - по ложительно определенная квадратная матрица параметр о, а» n; К,- Диагонал мая матри ца параметров внешнего конту ра; v(,) -функция, обеспечивающая робастность; x - входной вектор, состоящий из (qd, qdT, qdT, eT, eT)T размер)ностью nx x 1, nx = 5 • n, f (x) - описывается уравнением f (x) = W ■ o(H ■ x),                                                             (9)

где W - 1матрица весовых коэффициентов выходного слоя; H - матрица весовых коэффициен-тов скрыт ого слоя; <г ( . ) - активационная функция нейронов скрыто го слоя.

Весовы е коэффи циенты изменяют ся по следу ющим пр ав илам:

W = F ⋅ σ ⋅ r ^T

H=G⋅ x ⋅ (σ'TW⋅r) T где F и G - положительно определенные диагональные матрицы коэффициентов; о' - произво-д н ая от акт и в ац ионн ой ф^у н к ци и. П^ од ро б ное оп и са ни е алг о рит ма да^н о в [7].

,-..,,„

Дл я р еали зац ии подобной ада^пт ивн ой СА _^ У на б азе СИ М пред лагает ся стр _^ уктурная схема, приведенная на рис. 6. Компенсирующее воздействие Ат i ( к ) формируется симплексным инвари-антным методом по вектору ошибок e . В данной схеме ПИД-регулятор является классическим и описывается уравнением (2). При такой схеме возможно реализовать СИМ в n -мерном про-странс тв е и ли n СИМ в о^{^}д ном ерном пр о с тра нстве. В к ачес тве цел ево й ф ункц ии в постановке зад ач и адаптаци и (^3) испо льзуе тся ф _^ у нк ция

Q ( t )     = ¹    e ² ( t )

сим 2          , об еспечивающа^я постоянс т во градиен та в п ро цессе поиска.

Ис с ледовани е методо в адаптации

Проведем сравнительный анализ приведенных схем адаптации на двухстепенном манипуляторе (рис. 7), динамика которого подробно описана в работе [3], с параметрами: a 1 = 1, м; а ₂ = 1, м; m 1 = 2, кг; m ₂ = 0.5, кг; m 1 = 3.75, кг; B = 0.3, где a j - длина j -го звена, ш _у- - масса j -го звена, m, - масса груза в последнем звене, B - коэффициент трения в сочленениях.

Заданна^ я траектория описывается гар моническими во здействиями:

q d 1 = 20sin(o>t ), q d ₂ = 15sin(t yt ), co = 0.2тт,

dq d 1         dq d 2

q d 1 "            ’ q d 2 "

dt          dt

В качестве контролируемого возмущения прим ем время z ( к ) = к , к = 0... N , N = 1000. Время дис кр етизац ии T ^{^} 0 = 0.0 2 с , время моде ли рова н и я T =20 с.

Эф фектив ность мето^да адаптации оце нивается для каждог о сочленен ия функцией

N

J, = м Е V ^е ^( k ), j = 1’-’ n ’"                                             (13)

j N»1 j

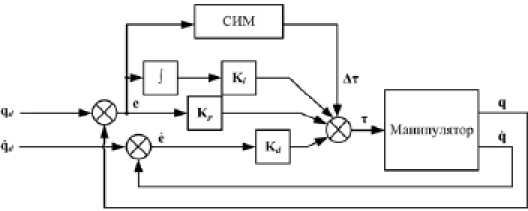
Рис. 6. Схема адаптивной САУ с корректировкой вектора моментов τ с использование СИМ (АдСАУ-СИМ)

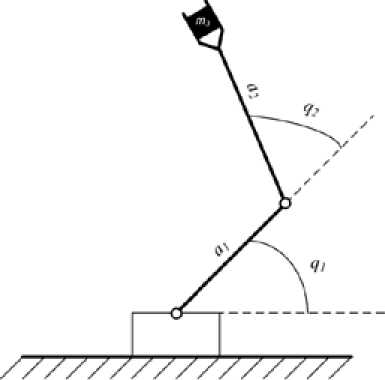
Р ис. 7 . К инематиче ская схе ма двухзвенного манипулятора

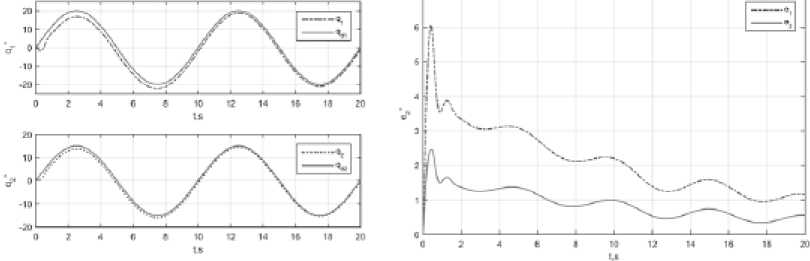
а ^ )                                                         б)

Ри с. 8 . Качество слежения П ИД: а – з ад анные и ре аль ные углы с очлен ений; б – ошиб ки с лежения в сочленениях

Для большей наглядности при вычислении показателя управления значение ошибки пере-водитс^ я из радиан в градусы, поэтому качество (13) представлено на рисунках и в таблицах в градусах.

Обычный ПИД-регулятор без адаптации ( ПИД) (см. рис. 1). Значения коэффициентов регулятора (2) равны K p ₀ = (1000 1000) T , K , ₀ = (100 100) T , K d ₀ = (75 75) T , A K p = A K , = AK , = (0 0). Результат ы раб оты П ИД-р егу^лятора для д вух звеньев показаны на рис. 8.

На ри с. 8 види м, что ошибка слежения первого сочленения всегда больше ошибки второго сочленения.

Эффективность адаптации J = ( J । J ₂ ) T = (2.1635 0.9102) T , град.

ПИД-регулятор с настройкой параметров нейронной сетью ( ПИД-НС ) (см. рис. 2). Нейронная сеть (см . рис. 3) в ыполняет фу нкцию регул ято ра . Активац ионная фу нкци я выходного нейрона

CT( x) =

2(1 - e ^a )

+ e ^а ) .

Функцию адаптера выпо.шяют выражения (4) с целевой функцией (3). Начальные значения коэффициентов регулятора K p ₀ = (1000 1000) T , K i = (100 100) T , K d = (75 75) T , векторы скоростей обучения равны n p = (600 800) T , П = (500 600) T , П d = (800 800) T .

Резул ьтаты р аботы алгоритма п редставлены на рис. 9.

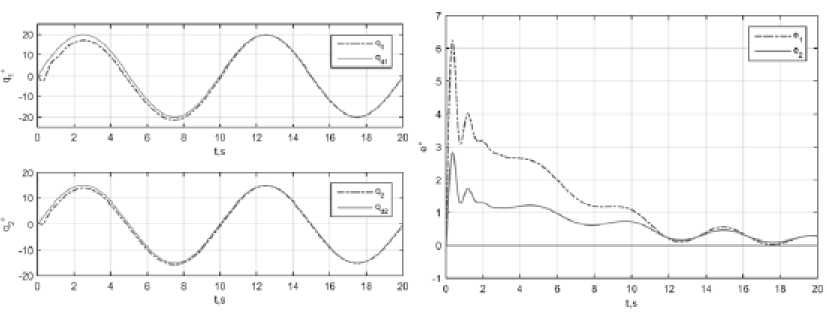
На рис. 9 видим, что ошибка слежения ПИД-НС в целом идентична ошибке ПИД-р егулятора, но спадает в о бла сть ма лых значений в два раза быстрее.

Эффективность адаптации J = ( J । J ₂ ) T = (1.4089 0.7173) T , град.

Адаптивная САУ с корректировкой вектора моментов т нейронной сетью ( АдСАУ-НС ) (см. рис. 4). Для моделирования использовали следующие значения параметров: количество слоев нейронной сети L = 2, количество нейронов во входном, скрытом и выходном слоях равны соответственно 1 1 =10, 1 2 =10, 1 3 =2, K v = 75 • 1 _{2 х 2} , А = 13.3 • 1 _{2 х 2} , 1 _{2 х 2} — единичная матрица размером 2 х 2, W - нулевая матрица размерностью 10 х 11, H - нулевая матрица размером 10 х 11.

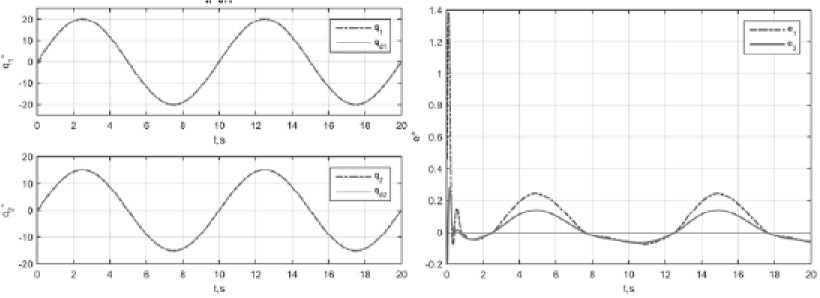
Результат исследования АдСАУ-НС представлен на рис. 10. Регулятор в пределах 1 с обеспечивает подстройку дополнительного воздействия Δ τ и удерживает ошибку слежения в области нуля. ПИД-регулятор с нейронной сетью имеет высокие показатели адаптации J = ( J , J 2 ) T = (0.11 0.07) T , град.

ПИД-регулятор с корректировкой вектора моментов дискретной нейронной сетью ( АдСАУ-ДНС ) . Система управления имеет такую же структуру, как АдСАУ-НС, за исключением нейронной сети, которая является дискретной. При моделировании использовалась однослойная нейронная сеть с l =25, А = 13.3 • 1 _{2 х 2} и временем дискретизации T 0 . Результаты работы АдСАУ-ДНС приведены на рис. 11.

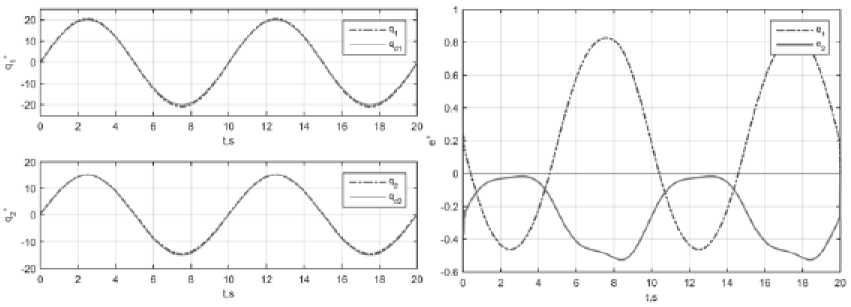
Эффективность адаптации J = ( J । J ₂ ) ^T = (0.44 0.25) ^T , град.

ПИД-регулятор с адаптацией симплексным инвариантным методом ( ПИД-СИМ ) (см. рис. 2). Регулятор – классический ПИД-регулятор (2). В качестве адаптера используется СИМ. Для каждого звена ведется независимый процесс адаптации по критерию (11). Поиск

а)

б)

Рис . 9. Качество с лежения ПИ Д-НС: а – з ад ан ные и реал ьн ые углы со _^ членен ий; б – ошибки с ле жения в сочленениях

а)

б)

Рис. 10. К ачество уп равления АдС^АУ-НС: а – зад ан н ые и реальн ые углы сочле нений ; б – ошибки сл еж е ния в сочленениях

а)

б)

Ри с. 11 . Качество управления А дСАУ-ДНС: а – з ад ан ные и реал ьн ые углы со^членен ий; б – ошибки слежения в сочленениях ведется в пространстве приращений (AKp, AKi, AKd). Начальны!е условия идентичны регулятору с настройкой нейронной сетью: базовые значения коэффициентов регуляторов равн ы Kp0 = (1000 1000)T, Ki0 = (100 100)T, Kd0 = (75 75)T. Стартовая точка симплекса находится в начале системы! координат пр) остранства поиск а. Начальная длина ребра симплекса равна L0 = (42 42) для пер в ого и вто р о^го зв еньев со ответственно и рассчиты вается исхо^дя из количест ва ша^гов поиска, пространственных ограничений пространства поиска (10) и условия, что начальная точка поиска лежит в центре этого пространства [8]. Конечная длина ребра симплекса выбиралась из минимально до пустимой о шибки поиска и равна LN = (0 .1 0.1) для обоих сочленений. Для оценки скорости дрейфа экстремума функции (11) используется рекуррентный алгоритм (6). Результаты работы приведены на рис. 12.

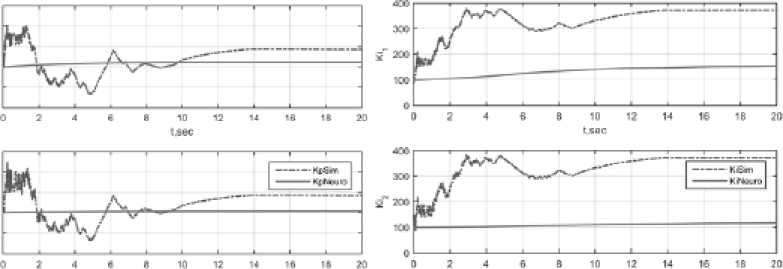
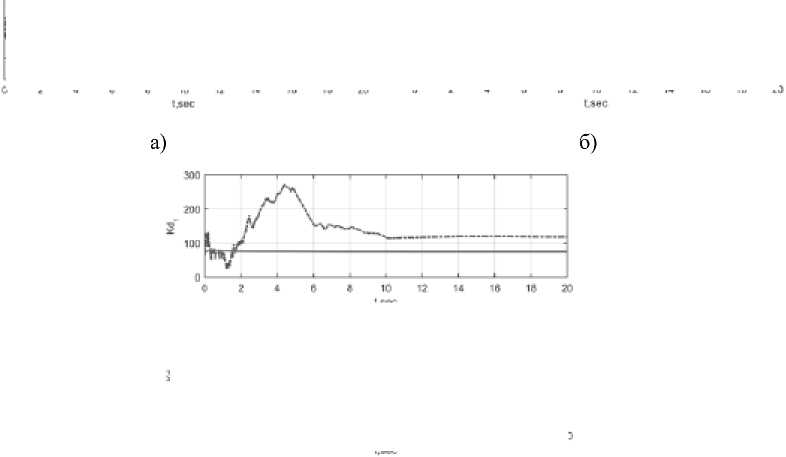
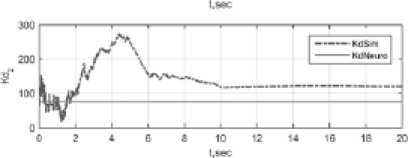
Дин ами ка измене ни я параметров при настройке ПИ Д- НС и ПИ Д-СИМ показана на рис. 13.

а)

б)

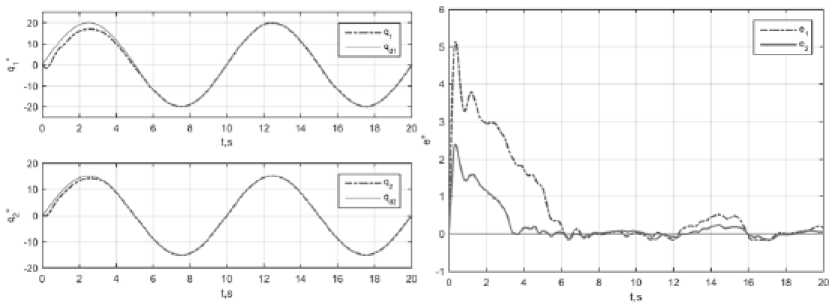
Рис. 12. Качество управления ПИД-СИМ: а – заданные и реальные углы сочленений; б – ошибки слежения в сочленениях

WOO

“

100(1

Й5Й

ООО

в)

Рис . 13. Динамика па ^{^} раметров при настр ойке нейрон ной сетью (не прерыв ная линия) и сим плексным инвариантным методом (пунк тирная лин ия): а – проп орционал ьн ый; б – интегральный; в – дифференциальный

Эффективность адаптации J = ( J । J 2 ) T = (0.750 8 0.3375) T , град. ПИД-СИМ показывает более высокую скорость достижения экстремума целевой функции по сравнению с аналогичным регулятором, использующим нейронную сеть. Это является следствием более активного изменения параметров во время настройки. Как видим на рис. 12 и рис. 13, при большой ошибке слежения происходит настройка, при которой параметры ПИД-СИМ изменяются в большем, чем у ПИД-НС, диапазоне значений. Чем больше значение ошибки слежения, тем больше значение параметров, что позволяет ПИД-СИМ быстрее устранить эту ошибку. Когда ошибка слежения близка к нулю, параметры ПИД-СИМ уменьшаются и в последующем либо не меняются, либо меняются незначительно.

Адаптивная САУ с корректировкой вектора моментов т с использование СИМ ( АдСАУ-СИМ )

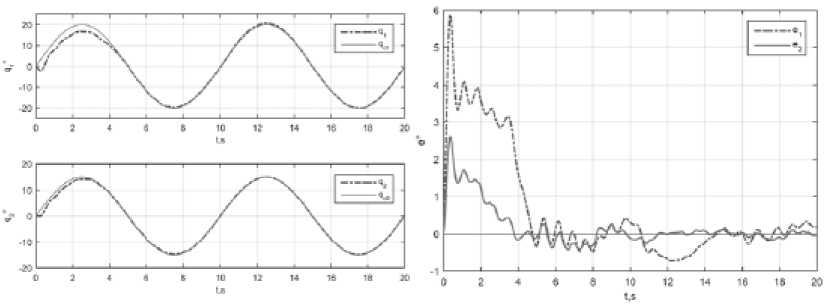
Параметры ПИД-регулятора равны базовым значения ПИД-НС, стартовая точка симплекса находится в начале координат поиска. Для оценки возмущения используется рекуррентный алгоритм (6). Для большей гибкости поиска для каждого звена применен одномерный симплекс. Начальная и конечная длины ребра симплекса вычисляется по тому же принципу, как для ПИД-СИМ, и равны L0 = (0.1 0.6), LN = (0.1 0.1). Результаты моделирования представлены на рис. 14.

Качество управления J = ( J । J ₂ ) T = (0.968 0233) T , град. АдСАУ-СИМ показывает схожую с ПИД-СИМ динамику ошибки при меньшем размере пространства поиска.

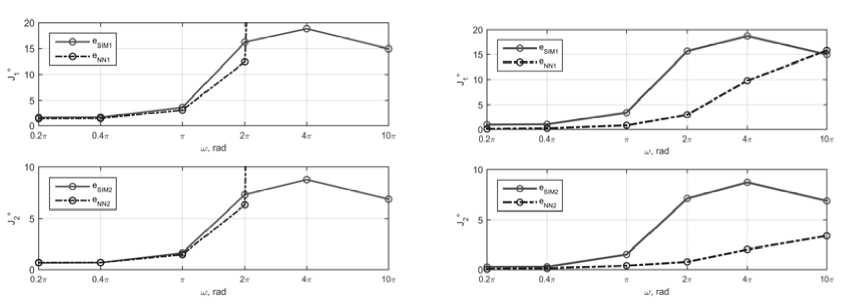
Определим частоту задающего воздействия, при которой обеспечивается устойчивость адаптации. Работоспособность регуляторов проверена при следующих значениях угловой скорости ω = {0.2, 0.4, 1, 2, 4, 10} в оздействия (12). Резу^льтат ы модел ирования пред ставлены на рис. 15.

Как видим на рис. 15 а на низких частотах входного сигнала ПИД-СИМ и ПИД-НС показывают со поставиму ю ошибку, н о с возраста нием ча стоты система с ад аптацией ней рон ной се тью теряет устой чиво сть, а регуля то^{^}р с адап тацией СИМ при схожих условиях сохраняет

а)                                                         б)

Рис. 14. Качество у правления Ад САУ-СИМ: а – з ад ан ные и реал ьн ые углы со члене ний; б – ошиб ки слежения в сочленениях

а)

б)

Ри с. 15. Среднекв адратичная ошибка упр авлени я в зависимости от час тоты задающег о воздействия для настройки ПИД-регулятора (а), для вычисления дополнительного воздействия Δτ (б)

а)

б)

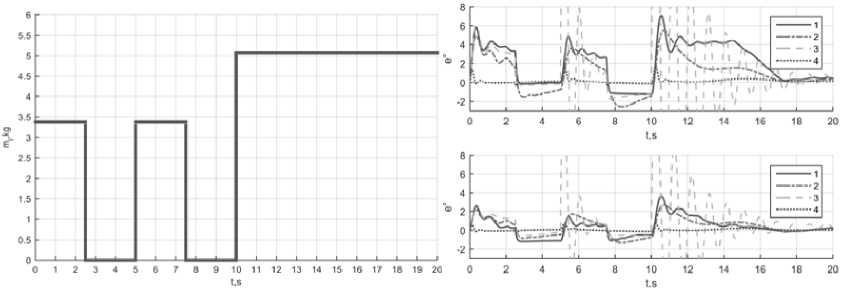
Рис. 16. Упр авление с переменной м ассой: a – гра фик измене ния м ассы; б – ошибка сле дования по траектории манипулятора с изменяющимися параметрами: 1 – АдСАУ-СИМ; 2 – П ИД-СИМ; 3 – ПИД-НС; 4 - АдСАУ-НС

устойчивость адаптации. Рис. 15 б показывает, что нейронная сеть обеспечивает более высокую точность управления на вы соких част отах, чем СИМ .

Проведены испытания алгоритмов в условиях изменений параметров манипулятора, а и менно масс ы груза m l , приложен н ой к коне^{^} чному зве ну манипу^{^}лятора. Парам е тр изменяется по следую щему зако ну:

3,38 кг , при t <  2.5;5 <  t <  7.5

m l = ^ 0 кг , при 2,5 <  t <  5;7.5 <  t <  10

5.07 кг , при 10 <  t <  20

Графики ошибок сложения ^при,е^доиы и, рис. 16 6 . Из ^розультато, моделирования следует, что АдСАУ-НС меньше всего подвержен влиянию изменения массы в схвате. ПИД-СИМ – 520 –

Показатели эффективности методов адаптации

№ Регулятор J1, град J2, град 1 АдСАУ-НС 0.11 0.07 2 АдСАУ-ДНС 0.44 0.25 3 ПИД-СИМ 0.7508 0.3375 4 АдСАУ-СИМ 0.968 0.233 5 ПИД-НС 1.4089 0.7173 6 ПИД 2.1635 0.9102 и АдСАУ-СИМ имеют схожие графики ошибки, несмотря на разные схемы управления, и заметно меньшую эффективность, чем у АдСАУ-НС. Алгоритм ПИД-НС склонен к большому перерегулированию и созданию колебаний.

Результаты работы рассматриваемых алгоритмов с постоянной массой нагрузки сведены в таблицу для удобства сравнения в порядке убывания.

При сравнении можно выделить АдСАУ-НС для настройки схемы с дополнительным воздействием и ПИД-СИМ для настройки параметров регуляторов, так как они показали наибольшую эффективность среди алгоритмов адаптации на рассмотренных схемах управления.

Заключение

Для проведения сравнительного анализа методов адаптации параметров регулятора системы управления робота-манипулятора:

• •    разработано программное обеспечение известных методов адаптации в среде MATLAB;

• •    разработано алгоритмическое и программное обеспечение метода адаптации на базе симплексного инвариантного метода;

• •    выделены зоны эффективного применения исследованных методов адаптации как первый шаг в формировании интеллектуальной системы управления роботом-манипулятором.

Проведенные исследование показали, что настройка параметров при помощи симплексного инвариантного метода приводит к управлению, которое обеспечивает ошибку на уровне адаптивных регуляторов на основе нейронных сетей. Установлены приоритеты использования алгоритмов при различных схемах управления.

Предлагаемые регуляторы, как и нейронные сети, не требуют знания динамических характеристик робота, и благодаря настройке в реальном времени система не теряет устойчивость даже при быстрых изменениях параметров манипулятора. Характерная черта рассмотренных адаптивных регуляторов – отсутствие необходимости в предварительном сборе данных и настройке параметров до начала работы. Преимуществом регуляторов, основанных на СИМ, является простота операций вычисления, что упрощает их задачу реализации во встроенных системах.