Сравнительный анализ методов аппроксимации функций в задачах обработки изображений

Задача восстановления зависимостей по эмпирическим данным в общей постановке выглядит следующим образом. Есть набор данных Х , каждый элемент которого характеризуется вектором признаков (параметров) ^ = ( x 1 , x 2 ,...x_N ), множество ответов Y и множество отображений (функций) U из X в Y. Существует отображение y * : X ^ Y , (не обязательно принадлежащее U ), значения которого априорно известны только на конечном наборе элементов y ( n ) = y * ( ^ ( n )), n = 1.. N (обучающей выборке). Требуется по априорной информации построить функцию y = f *(У, f * е U , наилучшим образом приближающую восстанавливаемую зависимость не только на элементах обучающей выборке, но и на всем множестве объектов X .

Мы будем рассматривать задачу восстановления регрессии, без ограничения общности подразумевая X = R K , Y = R используя среднеквадратичный критерий близости как функционал качества:

• ^е 2 = Е ⁽ У ⁽ n ) ^- f *® n ^{))) 2                      (1)}

n

Конкретный вид класса U алгоритмов (функций регрессии) во многом определяется исследователем на основе специфики задачи. Наиболее распространенными вариантами является восстановление в классе линейных по параметрам функций [1,3,5] (и как частный случай линейной и полиномиальной аппроксимации), нейронные сети [2,4], древовидная аппроксимация [3,5] и др. Целью данной работы является их экспериментальное сравнение в применении к задачам фильтрации изображений.

Линейные по параметрам аппроксимирующие функции

Будем искать аппроксимацию в классе линейных по параметрам функций:

M

• ^y = E a i ^f i ^{( Х} 1 , ^Х 2 ,... ^X K )’                         ⁽²⁾

i = 0

Оптимальная система коэффициентов A = { a_k } K = 0 , минимизирующая критерий (1), находится по методу наименьших квадратов за один проход по обучающей выборке:

BA=C ,                                   (3)

где

• f N - 1                    1 M ^{- 1}

в =1 E fk №)) fl (^(n)) ^

I ⁿ = ⁰ k , l = 0

f N-1

^B m , i = ^B i , m =1 E ^fi (^(ⁿ⁾⁾ r     , ^B M , M = ^N ,

In=0

f n-1                  1 M-1

C =1 E ^fk K⁽ⁿ⁾⁾ ■ y ⁽ n ) f     , C m = E ^{y ( n} ).

I n=0                    J k=0

Таким образом, можно выписать аналитические выражения для A = { a k } k = 0 и ошибки аппроксимации ε²:

A = { a k } k = 0 = B - 1 C, е ² = j N ( y - C T B - 1 C ) ,

N - 1

где Y =E У 2(n).

n = 0

Нейронная сеть

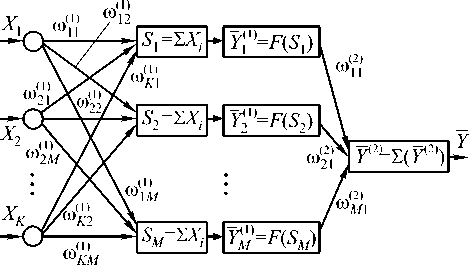
Используем нейронную сеть с K входами, одним скрытым слоем ( M нейронов в скрытом слое) и одним выходом (Рис.1):

Для подстройки весов - коэффициентов синоптических связей w_i ⁽ _j ^{k )} , где k - индекс номера слоя, i и j – индексы нейронов слоя k и ( k +1), использовался известный алгоритм обратного распространения ошибки (back propagation) [2,4],который в случае двухслойной нейронной сети выглядит следующим образом:

wj) (n) = wj) (n 1) ПдЛ, k) (n),k = I,2, fwi)

( n ) = [ y ⁽²⁾ ( n ) - Y ( n ^C n ), d w - )

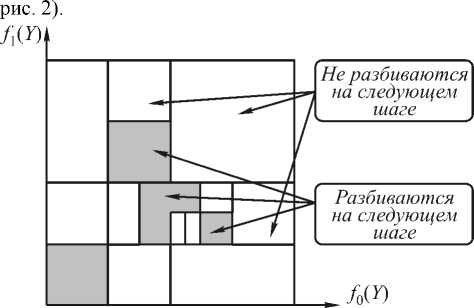
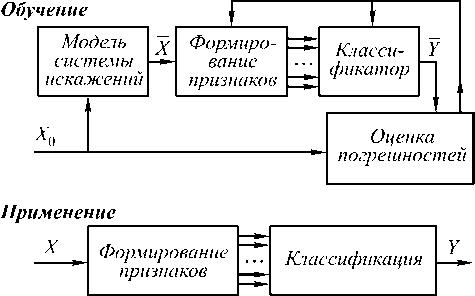
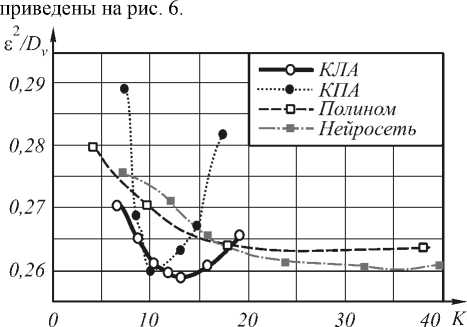
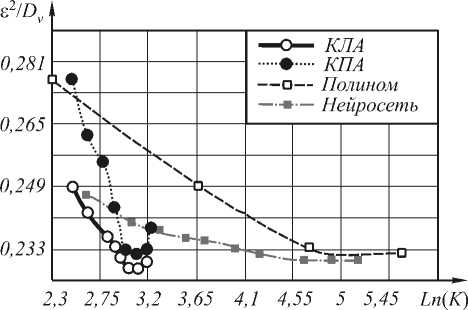
(n) = [Y<2) (n) - Y(n)]w<2) (n)Xt (n)F (Yj (1> (n)) dwj где n — коэффициент скорости обучения, 0

Вход

Скрытый слой

Выход

Рис. 1. Схема нейронной сети

В качестве активационной функции были исследованы следующие функции:

Функция Ферми:           y = f⁽⁵) = i ₊e_₅

Гиперболический тангенс: y = f⁽⁵) = th⁽⁵)

Рациональная функция:

У = f⁽⁵) = ¹

^{1 +}1⁵1

Линейная функция:           y = f (5) = 5

Критерий остановки итерационного процесса настройки весов - либо уменьшение ошибки до некоторого, наперед заданного, порога, либо отсутствие изменения ошибки в течении длительного времени.

Иерархическая аппроксимация

В процессе построения функции аппроксимации область определения, представляющая собой K-мерный гиперкуб, последовательно разбивается по осям и порождает в памяти ЭВМ древовидную структуру [5] (см. "двумерную" иллюстрацию на

Рис. 2. Схема разбиения признакового пространства

Каждый последовательный шаг разбиения включает следующие этапы:

• 1.    оценка перспективности деления вершин на основе ошибки аппроксимации в них;

• 2.    деление (образование новых терминальных вершин);

• 3.    проход по обучающей выборке и накопление статистик для новых вершин по элементам выборки, попавшим в них;

• 4.    построение функции аппроксимации и вычисление ошибки в новых вершинах.

В работе использовались два вида функции аппроксимации в терминальных вершинах дерева.

• 1)    Аппроксимация постоянным значением:

Оптимальный коэффициент аппроксимации:

• 1    I-1

a =— Y (j), ‘тт                 ,

Ij j=0

где Y(j) - подмножество точек выборки из набора Y попавших в j-ую терминальную вершину, Ij - их количество.

• 2)    Линейная аппроксимация.

Воспользовавшись выражением (2) для f (x1,X2,—X_K) = x, получим линейную аппроксимацию. Оптимальные коэффициенты a_i в каждой вершине найдем по МНК, решив систему (3) в каждой из терминальных вершин получившегося дерева.

Применение методов восстановления регрессии для задач фильтрации изображений

Рассмотрим использование аппроксимации функции решения на примере задачи фильтрации изображений от шума в случае, если априорная информация (желаемый результат обработки) задается в виде согласованной пары изображений, интерпретируемых как "входное" X и "выходное" Y. Требуется восстановить изображение Y по X, однако на практике в результате обработки удается получить результат Y - аппроксимацию Y. По паре изображений Yu X, используемых в качестве обучающей выборки, строится восстанавливающая процедура, состоящая из формирования по X набора изображений - признаков ^ = (X 1, X2,...XK) и построения функции аппроксимации Y = f (X 1,X2,...xN).

Тогда задача фильтрации (получение оператора преобразования f*) - сводится к задаче восстановления регрессии, если рассматривать в качестве обучающей выборки отсчеты заданной пары изображений. При этом сначала по искаженному изображению формируется K-мерный вектор признаков-изображений £(n 1, n₂) = {xk (n 1, n₂)}K=1, а затем, на его основе, вычисляется оценка отсчетов результирующего изображения (см. рис. 3).

При построении f* по обучающей выборке минимизируется сумма квадратов разностей между отсчетами идеального и полученного изображений.

Рис. 3. Общая схема преобразования данных.

Экспериментальные исследования

В качестве исходного материала использовались две последовательности согласованных пар "идеальных" и зашумленных изображений с разными реализациями шума (отношение "сигнал/шум" Dx/Dv=5). Тесты проводились на двух изображениях, размером 512×512 отсчетов. Первое изображение – «Портрет» представлено на рис. 4. Второе изображение – «Космический снимок» представлено на рис. 5.

Рис. 4. Изображение «Портрет»

В первом эксперименте сравним описанные выше способы аппроксимации на небольшом количестве признаков – 2 признака. В качестве признаков используем зашумленное изображение и зашумленное изображение, сглаженное Гауссовским фильтром.

Во втором эксперименте увеличим количество признаков до пяти. Добавим производную Гауссовского размытия, медианное сглаживание и зашумленное изображение с подчеркнутыми границами.

При этом для сравнения были взяты методы с одинаковой сложностью решающего правила при применении методов. В качестве сложности применения взят критерий количества операций на отчет.

Для нейронной сети количество операций на отчет равно K=(M+2)N+1 операций/отчет, где M – число признаков, N – количество нейронов в скры- том слое. Для иерархической аппроксимации количество операций на отчет равно К=H+L опера-ций/отчет, где H – средняя глубина дерева, L – количество операций в терминальной вершине (одна операция для КПА и 2M операций для КЛА).

Рис.5. Изображение «Космический снимок»

Для полиномиальной аппроксимации можно вычислить сложность по следующей формуле:

N-1 N    N

• K = 2ZZ... Z1,

i1 =0 i 2 =0 iM-1 =0

где M – количество признаков, N – степень полинома;

В качестве критерия качества фильтрации использовался коэффициент понижения шума –

• 8 ² / Dv .

Результаты эксперимента 1 на изображении

«Портрет» приведены на рис. 5. Результаты эксперимента 2 на изображении «Космический снимок»

ис. 6. Сравнение различных типов аппроксимации на 2-х признаках.

Таким образом, иерархическая аппроксимация показывает лучшие результаты, нежели остальные методы. Нейронная сеть стабилизируется на сложности около 40-50 операций на отчет (15 нейронов)

в случае 2 признаков и на сложности 150-200 (20-25 нейронов) операций на отчет в случае 5 признаков.

Рис. 7. Сравнение различных типов аппроксимации на 5-ти признаках.

Кроме того, построение иерархической функции аппроксимации происходит значительно быстрее, чем обучение нейронной сети и построение полинома. В среднем построение дерева сложности 25-30 операций на отчет соответствует 3-10 итерациям обучения, подобной по сложности, нейронной сети (по проведенным экспериментам для нормальной работы нейронной сети необходимо несколько тысяч итераций обучения), а так же соответствует по сложности построению полинома 3 порядка.

Заключение

Во всех проведенных экспериментах иерархическая аппроксимация функции решения продемонстрировала свои преимущества по сравнению с обще- известными алгоритмами. И кусочно-линейная и кусочно-постоянная аппроксимация обладают лучшим качеством аппроксимации, чем нейронная сеть или полином при равной сложности применения. Кроме того, способ иерархической аппроксимации демонстрирует более высокую скорость построения функции аппроксимации, чем нейронная сеть или полином.

Работа выполнена при поддержке Министерства образования РФ, Администрации Самарской области и Американского фонда гражданских исследований и развития (CRDF Project SA-014-02) в рамках российско-американской программы "Фундаментальные исследования и высшее образование" (BRHE); а также при поддержке Российского фонда фундаментальных исследований (РФФИ), проекты №№ 03-01-00736, 05-01-96501.