Сравнительный анализ методов оценки эффективности обучения

Процесс создания современной авиационной техники, а также ее дальнейшая безопасная эксплуатация требует повышенного внимания к компетенциям специалистов, задействованных работах на различных этапах жизненного цикла изделий. В ряде работ [1, 2], в которых освещены вопросы повышения уровня компетенций работников авиационной промышленности, наибольшее внимание уделено техническим и методическим аспектам обучения. С другой стороны вопросы связанные с контролем знаний не менее важны.

Традиционными методами контроля степени освоения обучающимися преподаваемого курса являются промежуточные зачеты с оценками «зачет»/«незачет» и экзамены с оценками чаще всего в пятибалльной системе: 5 – отлично; 4 – хорошо; 3 – удовлетворительной; 2,1 – плохо и очень плохо.

Однако более детальный анализ эффективности обучения показывает, что на результаты тестирования и контроля оказывает большое количество факторов [3,4]: здесь и степень освоения обучающимися предшествующих курсов, связанных с преподаваемой дисциплиной и их

индивидуальные особенности (способность к аналитическому мышлению, внимательность и сосредоточенность, навыки работы с литературой и пр.). Большое значение имеет профессионализм преподавателя, его умение производить декомпозицию сложной проблемы на более простые составные части, контакт с аудиторией и пр. Поэтому простейшего анализа результатов проведения зачетов и экзаменов недостаточно – необходим более детальный анализ отдельно уровня сложности преподаваемой дисциплины и согласованным с ним уровнем подготовленности обучающихся. При этом наиболее часто используется математический аппарат дисперсионного анализа, как минимум – двухфакторного.

• 1.    ОСНОВНЫЕ ПОЛОЖЕНИЯ ДВУХФАКТОРНОГО ДИСПЕРСИОННОГО АНАЛИЗА

В табл. 1 приведено расположение данных в двухфакторном плане проведения эксперимента [5-7].

Здесь введены обозначения:

bn1

• У к. = ££ y jk , y . = ЬПУ..., i = 1,2, - , a ;

an1

y j = T^ y jk , y j . =    y . j . , j = и,-, b ;

i = 1 k = 1

n 1

• У у. =Z yjk , yj. =-Уу., i = 1,2,-, a , k=1

j = 1,2, - , b ;

abn1

y ... = EEE y «k , ^y .. =      y .. , ^k = ^{1,2, - , n} .

и 7=1 k =1           ^abn

Таблица 1. Расположение данных в двухфакторном плане

		Фактор В
		1	2		b
Фактор А	1	y lll • • • y lln	y l2l • y l2 n		y l b l • y l bn
	2	y 2ll • y 2l n	y 22l • y 22 n		y 2 b l • y 2 bn
	a	У а ll • У а l n	У а 2l • У а 2 n		У аЬ l • y abn

Общая сумма квадратов разлагается на сле-

дующие слагаемые:

abn           a           b

ЕЕЁ( у» - yJ = bn Z( y...-y.J2+an E( y>- yJ+ i=1 j=1 k =1                              i=1                             j=1

ab            abn

+nLZ(У,.-у..-У..-+yJ +SEE(y,k-j • i =1 j =1                                           i=1 j=1 k=1

или в новых обозначениях:

.V2 = X2     2     2      2

общ.     A + B + AB + ошибк., т.е. происходит разбиение на суммы квадратов, обусловленное «строками» или факторами А, «столбцами» или факторами B, взаимодействием между факторами А и B, ошибкой.

Число степеней свободы, соответствующих каждой сумме квадратов, составляет:

Фактор	Число степеней свободы
A	a — l
B	b — l
AB	( a — 1 )( b — l )
Ошибка	ab ( n — l )
Сумма	abn — l

Из анализа числа степеней свободы видно, что для различения между эффектом взаимодействия и ошибкой n >  2.

Наблюдения в двухфакторном дисперсионном анализе описываются линейной статистической моделью yjk = H + 6i + Pj + (6p)j + ^yk; i = 1,2,—, a ;

j = 1,2, - , b ; k = 1,2, - , n              (2)

H - математическое ожидание эффекта;

6 i - эффект i -го уровня фактора А;

, j. - эффект j -го уровня фактора В;

C,_yk - случайная ошибка.

Различают два вида модели (2): модель постоянных эффектов и модель случайных эффектов. При использовании модели постоянных эффектов результаты дисперсионного анализа применимы только к рассматриваемым уровням факторов; при использовании модели случайных эффектов результаты распространяются на всю область изменения факторов. Возможны также смешанные модели, когда уровни одного фактора выбираются случайным образом, а уровни другого – фиксированы. Различия в моделях имеет значение при расчете мощности критериев дисперсионного анализа, оценки компонент дисперсии; решающие правила о значимости или не значимости влияния каждого из факторов и их взаимодействий одинаковы для всех моделей. До сих пор не делалось никаких допущений о законах распределения вероятностей применимых в модели (2).

В классическом дисперсионном анализе применимы следующие допущения [6]:

• -    в модели постоянных эффектов ab

Z е,= О ; а= О, т.е. для фиксированных /=i                 j=i факторов эффекты определяются как отклонения от математического ожидания ц;

• -    в модели случайных эффектов принимаются нормальные законы распределения вероятностей 6 ~ N (О;а ²); В~ N (О;а ²);

  /                     у               j                     ^р

( ⁶P ) , ~ N ( 0;^ , ) ;

• -    в обеих моделях ошибка считается нормально распределенной случайной величиной

• 2.    ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ ЭФФЕКТИВНОСТИ ОБУЧЕНИЯ

s j ~ N ( ^О;° 0 ) .             (3)

Однако, общий принцип проведения дисперсионного анализа на основе разложения общей суммы квадратов на компоненты не требует указанных выше ограничений.

В ДИСКРЕТНОЙ БИНАРНОЙ ШКАЛЕ

При оценивании результатов контроля обучающихся (тестировании в бинарной шкале) случайные величины y_ijk могут принимать только два значения: 1 – при правильном ответе на контрольный вопрос и 0 – при неправильном.

Статистики двухфакторного дисперсионного анализа могут быть построены на основе статистики x2 Пирсона, применяемой в основном как критерий согласия между эмпирическими и теоретическими распределениями [5].

Пусть m_C – число наблюдаемых событий, а p_C – гипотетические вероятности мультиномиального распределения

P ( ^m _x , _ ,mclP i , _ , P c , n ) ~

Тогдаx² =

L (mk - nPk )2

k = 1      nP k

- х2-распределение

с ( C –1) числом степеней свободы.

Оценками вероятностей p_k являются оценки вида p_k = m_k/n .

Нулевая гипотеза принимается при X ² >  XL ( ^C - 1 ) , где xL ( ^{C -} 1 ) ^- квантиль Х²-распределения уровня значимости а и ( C -1) числом степеней свободы.

При измерениях результатов ответов обучающихся в номинальной шкале табл. 1 примет вид, представленный в табл. 2.

Здесь в каждой ячейке содержится одно из-

условии равномерного их распределения между строками и столбцами.

Для построения статистики дисперсионного анализа при измерениях в номинальной шкале необходимо разделить суммы S_a ² и S_b ² на ожидаемое число событий

2            V2

xL ( c -1) zA = Say ;z^ = Syr • ma   mb

Числа ma и mb могут получаться дробными, поэтому более удобная для практического использования вероятностная интерпретация:

p, =

m

b

= m ; p • j =

a

мерение 0 или 1 ( n = 1 ) ;

Тогда X A =

b У, Pi ^- p .

mm

-=- = m ; p .. =     .

a j ab

A2

V i = 1

– с числом сте-

m i . - число правиль-

p

ных ответов i -ого обучающегося на все во-

просы; m . j - число правильных ответов всех обучающихся на j вопрос.

Как было отмечено выше при n = 1 выделить эффект взаимодействия не удается, и двухфакторный эксперимент сводится к двум однофакторным, т.е. вычисляются суммы

пеней свободы ( a - 1 ) , и z ² =

– с числом степеней свободы

a E P

- P ..

P.

a                               b ₂

S a = b L ( У ^ ^- У )² , S b = a L ( y j ^- y n )

.

i = 1

В рассматриваемом случае

у = 1

s ² = ь у m - a                         •

a

- L m• a ,=1

a

= - У m b LI *

^^^^^^^в

a

- L m• a ,=1

,

S b ² = a Ъ

1 ^b

m,— У m j                        • b i=1

■ j

где L m i • = L m . j = m • ab

1 A

=-L m

^^^^^^e

1b m ьL •

• j

,

Таким образом m i . , m, j представляют собой экспериментальные числа событий соответственно в i -ой строке (для i -ого обучающегося) и в j -ом столбце (для j -го вопроса), а числа ma и mb ожидаемые числа событий при

Пример 1

В табл. 3 приведены результаты статистического моделирования при a = 10 ; b = 10; вероятность успешного ответа всех обучающихся на все вопросы 0,5. Общее число положительных ответов меньше 50, что определяется статистической погрешность. Общее число положительных ответов распределяется между вопросами и обучающимися в соответствии с равномерно распределенными случайными числами x_y <  0,5 принимается y jj = 0 , при х_у >  0,5 принимается у _у = 1 . Ожидаемый ответ после проведения дисперсионного анализа: сложность вопросов и подготовленность обучающихся не влияет на результаты контроля.

a

Ю£ ( т_ь - 3,9 )

X a =    ⁱ = ¹ ₃₉ ------* ^? ,923 <  X» ( 9 ) = 14,7 ,

Таблица 2. Результаты тестирования обучающихся в двухфакторном плане в номинальной шкале

		Вопросы
		1	2	- j"	b	m v
5 3 3 2 о	1					mV.
	2					m 2 •
	: i
	a					ma.
	m • j	m1	m . 2		m b	E mi • = E m • j = m ab

Таблица 3. Результаты статистического моделирования задачи двухфакторного эксперимента

Вопросы 1 2 3 4 5 6 7 8 9 10 mi. 1 0 0 1 0 0 1 1 0 0 1 4 2 0 0 1 1 0 0 0 0 0 1 3 3 0 1 0 0 0 0 0 0 0 0 1 4 1 0 0 1 0 0 1 1 0 0 4 5 0 1 1 0 1 0 1 0 0 1 5 6 1 1 0 1 0 0 1 0 0 0 4 7 0 0 0 1 0 0 1 0 0 0 2 8 1 1 0 1 1 1 1 1 0 1 8 9 1 0 0 0 1 1 0 0 1 0 4 10 1 0 0 1 0 0 1 0 1 0 4 mj 5 4 3 6 3 3 7 2 2 4 39 b-.                  \2

Ю£ ( т, - 3,9 )

Z b = ^=^-----* 6,385 <  / 0,9 ( 9 ) = 14,7 .

• 3,    9

Таким образом, полученный результата анализа совпадает с ожидаемым, т.е. экспериментальные данные согласуются с их ожидаемыми значениями и ни один из факторов не оказывает влияния на результаты контроля обучающихся.

Однако даже в данном примере видно, что значение / В дальше отстоит от процентной точки х^, чем значение / л , т.е. данные столбцов (фактор сложности вопроса) более согласован с ожидаемыми значениями, чем данные строк (фактор подготовленности обучающихся).

В общем случае обработки экспериментальных данных возможны решения о значительности влияния как сложности вопросов, так и подготовленности обучающихся. При этом традиционно возможны лишь два решения: наличие или отсутствие такого взаимодействия.

При оценке эффективности обучения нас интересует не только наличие влияния исследуемого фактора, но и степень этого влияния.

Для оценки степени влияния может быть предложен подход, описанный в [8].

X2 - критерий согласия относится к группе критериев значимости, построенных на следующих общих принципах:

• -    выбирается некоторая статистика (функция от экспериментальных данных);

• -    на основе теоретических исследований принимается нулевая гипотеза о теоретическом законе распределения вероятностей данной статистики;

• -    определяются области малых вероятностей (критические области), в которых согласно принципу практической невозможности осуществления маловероятного события не должно попасть экспериментальное значение статистики;

• -    если значение статистике не попадается в область малых вероятностей, определяемой выбранным уровнем значимости, то такое событие не противоречит принятой нулевой гипотезе и последняя может быть принята;

• -    выбор условия значимости в практических приложениях достаточно произволен и составляет а = 0,05 ^ 0,1 .

• 3.    ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ ЭФФЕКТИВНОСТИ ОБУЧЕНИЯ

Предлагаемый подход состоит в следующем. Используемые статистики (в т.ч. и х2 -критерий) достаточно часто имеют бесконечные шлейфы (X2 имеет бесконечный правый шлейф).

В результате всегда можно подобрать такое значение а, назовем его критическим а _кр , для которого нулевая гипотеза принимается. При этом малым значениям а _кр соответствует большая область принятия нулевой гипотезы и наоборот. Широкая область принятия нулевой гипотезы соответствует большому допустимому рассогласованию между экспериментальными и теоретическими данными, что сказывается на достоверности принимаемого решения. Таким образом, величина а _кр может быть принята как оценка адекватности теоретической модели экспериментальным данным.

В рассматриваемом выше примере с точностью до табличных значений процентных точек х²-распределения для фактора А а _кр= 0,5; для фактора В а _кр= 0,7. Таким образом фактор А более сильно влияет на результат тестирования обучающихся, чем фактор В.

В НЕПРЕРЫВНОЙ ШКАЛЕ

В случае, если ответы обучающихся на вопросы оцениваются в баллах т.е. имеется более полная информация, чем в бинарном случае, для оценки эффективности обучаемых используется традиционный двухфакторный диспер- сионный анализ, методика проведения которого широко известна и опубликована в ряде фундаментальных работ [5-7].

Поэтому в данном разделе остановимся лишь на нарушении исходных предпосылок при проведении этого анализа.

В начале обучения степень подготовленности обучающихся принимается обычно нормально-распределенной, при небольшом количестве как слабо подготовленных, так и сильно подготовленных слушателей. При этом программы обучения подготовленная для среднего обучающегося будет слишком сложной для первых и слишком простой для вторых. По мере обучения число хорошо подготовленных слушателей смещается вправо, т.е. происходит переход от нормального распределения к асимметричному распределению с положительным показателем асимметрии.

Далее при контроле стандартного курса обучения вопросы обычно подбираются одинаковой сложности. Для оценки сложности, при этому отсутствуют какие либо рекомендации по составлению числа вопросов уменьшенной, средней и повышенной сложности. В перечисленных условиях ограничения (3) в виде нормальности распределений явно нарушается.

Ниже прилагается универсальный подход двухфакторного эксперимента, не связанный с какими-либо предположениями о законах распределения исследуемых факторов и погрешности измерений, основанный на использовании эмпирических вероятностях результатов контроля обучающихся.

Для большей наглядности изложим предлагаемый подход на данных примера 1.

Пример 2.

Пусть оценивание знаний обучающихся производится в 10-ти балльной шкале и гипотетические результаты (в баллах) будут:

• -    по столбцу: т . = { 4,3,1,4,5,4,2,8,4,4 } ;

• -    по строке: m . j = { 5,4,36,3,3,7,2,2,4 } .

Приравняем значения баллов приближенные эмпирические вероятности, полученные из условия равномерного распределения:

• -    по столбцу: 4/10; 3/10; 1/10; 4/10; 5/10; 4/10; 2/10; 8/10; 4/10; 4/10;

• -    по строке: 5/10; 4/10; 3/10; 6/10; 3/10; 3/10; 7/10; 2/10; 2/10; 4/10.

В результате приходим к предыдущему плану двухфакторного дисперсионного анализа в бинарной шкале.

Более строго по данным столбца и строки можно построить эмпирические функции распределения.

Для этого располагаем данные в вариационный ряд:

• -    по столбцу: 1; 2; 3; 4; 4; 4; 4; 4; 5; 8;

• -    по строке: 2; 2; 3; 3; 3; 4; 4; 5; 6; 7.

Каждому i -ому значению столбца или j -ому значению строки будет соответствовать i несмещенная оценка вероятности pi =---- и n +1

p - = ^j , где n - объем выборки, в данном ^j n + 1

примере n = 10.

Одинаковым значениям приписывается средняя вероятность. Возвращаясь к первоначальному расположению данных, получим:

• -    по столбцу: 6/11; 3/11; 1/11; 6/11; 9/11; 6/11; 2/11; 10/11; 6/11; 6/11;

• -    по строке: 8/11; 6,5/11; 4/11; 9/11; 4/11; 4/11; 10/11; 1,5/11; 1,5/11; 6,5/11;

• 4.    ЛОГИСТИЧЕСКАЯ МОДЕЛЬ ГЕОРГА РАША

Проводя далее расчеты по методике двухфакторного плана в бинарной шкале, получим:

/ ■ 11,98 <  14,7 ,

/ В - 13,36 <  14,7 .

Таким образом, гипотеза по незначимости влияния уровня сложности и уровня подготовленности обучающихся принимается, однако с меньшим критическим уровнем значимости, чем в предыдущем примере, что свидетельствует о большой чувствительности данного подхода к возможным погрешностям.

Однако более эффективной является логистическая модель Г. Раша.

Бельгийский математик Г. Раш предложил в качестве модели оценки эффективности и сбалансированности обучения логистическую модель [9]

p ( е - р ) = ^ехр «* ^{- 11} »

• 1    + ехр {(е - р)}’

  
  

где в - уровень сложности контрольного задания, 0 - уровень подготовленности слушателей.

При организации активного эксперимента возможна оценка степени подготовленности группы обучающихся при фиксированной степени сложности и наоборот при фиксированном составе группы. При этом компоненты модели Раша могут быть заменены эмпирической оценкой вероятности по частоте р = mJ a , е = m/b . Формирование этих оценок было ранее описано в докладе в разделе 2.

Покажем, что эта модель является универсальной и может быть использована для анализа результатов тестирования как в бинарном случае, так и при оценивании в баллах.

В [8] для эмпирической функции распределения предложено следующее нормализующее преобразование:

p u = in------.                (5)

^{1 -} Р

Обозначив случайную величину u = 9-в из (5) получим:

rp- = ехр {(9 - р)};

1 - p

p = (1 - p) ехр{(9 - р)};

_ ехр{(9 - р)}

Р 1 + ехр {(9 - р)} ’ т.е. модель Раша.

В процессе подготовки операторов к работе со сложной техникой к обучающимся предъявляются чрезвычайно высокие требования к качеству освоения преподаваемого материала. При этом одноразового обучения зачастую недостаточно и возникает вопрос о планировании всего процесса подготовки, а в частности в определении оптимального объема циклов обучения.

Данная задача может быть решена с использованием хорошо известных моделей роста надежности. Задача оценки динамики эффективности обучения по постановке близка к задаче оценки динамики надежности изделия в зависимости от числа циклов испытаний, после каждого из которых производится доработка изделия с целью устранения выявленных в процессе испытаний дефектов, повышая его надежность. Действительно, контроль знаний обучающихся может рассматриваться как их испытание, а выявленные неосвоенные фрагменты курса как дефекты обучения, требующего их повторного освоения и доработки.

При использовании моделей роста надежности остановим свой было на логистической модели роста, что является логичным и естест-нывенным с учетом логистической природы модели Раша. Логистическая модель роста надеж- ности имеет вид:

R(n) = -

R 0

R 0 + ( 1 - R 0 ) exp ( -Q п ) .

При числе циклов п = 0 , R = R ₀ ; при п ^ го , R ^ 1 .

Нетрудно видеть, что модель (6) является частным случаем модели (4), когда R ₀ = 0,5 , п = 1 , Q = 9-0 и рассматриваются только положительные значения Q, приводящие к росту надежности R . Кроме этого в модели (6), параметр Q = const , а в модели (4) 0= 9-0 - случайная величина, косвенное измерение которой осуществляется на основе оценки вероятности P по частоте.

Модель (6) может быть записана в эквивалентном дискретном рекуррентном виде

R =      Ri-1 exP {Q} i Ri-1 exp {Q} + (1 - R-1)’ откуда после несложных преобразований получим in Ri- = in Ri-1 + Q, qi и окончательно переходя к обозначениям модели (4), получим уравнение прогнозирования на 1 шаг:

In p_ = In pi-L + (9^ - pz i),(7)

q.q где (9i-1 — Pi-1) - оценки, полученные путем обработки информации на предыдущих циклах вплоть до (i -1) включительно.

Заметим, что здесь используется простейшая линейная модель зависимости показателя роста Q i от числа циклов:

Ц=( о - р) п.

В качестве оценок случайной величины ( 9 i _{- 1} - P i _{- 1} ) рационально использовать среднеарифметическую оценку

Q

i - 1

-4 z in j.

n - 1 j = 1 Q j

Уравнение (7) может быть расширено для прогнозирования на более, чем один шаг вперед, например:

In p" = In p-L + ( 9, - 1 - P , - , ) ■ 2

q i + 1         q i - 1

и т.д.

Далее модель Раша может быть использована для анализа влияния факторов сложности контрольных заданий и подготовленности обучающихся как в дискретной, так и в непрерывной шкалах, в зависимости от вида получаемой информации.

Пример 3.

Пусть заданное значение Рза3анное= 0,99, т.е. 0 99

in---- = 4 595 . Далее, пусть, значение in — ,

0,01    ’ полученное после проведения первого ознакомительного контроля знаний составляет:

Inp- = In9^ = 9’495 = 9 -р,, т.к. в (7) q1     9’4

in p ⁰ = in ⁰⁵ = 0 .

q0

Тогда после второго цикла обучения ожидается достижение значения in — = 0,405 • 2 , Q 2

p = 2,25 , откуда P = 0,692 .

q 2

При таком темпе роста надежности для достижения Р_{заданное}= 0,99 потребуется 4,595 - 0,405 = 0,405 • n циклов обучения, откуда n « 10 .

Пример 4. Пусть подготовленность группы обучающихся выше и составляет р 1 = 0,8 . Тог- ln ⁰⁸ = ^1,386 и Для Достижения ^Р заЗанное = ^0,99 да 0,2

потребуется уже n ~ 3 циклов обучения.

Пусть далее, при проведении тестирования на 2-ом цикле получено 90 правильных ответов,

-   90

т.е. P =----= 0,9 .

Нижняя доверительная граница при у = 0,9 составит:

0,9-04

Р_н = 0,9 - 1,28. Р---- ,- « 0,862 ,

^H              100

откуда

0₂ - р₂ = In⁰⁸⁶² - In⁰⁷⁵ = 1,832 - 1,099 = 0,733 .

• ^{2   2}      0,138     0,25

Средний темп роста составит при этом

При практическом использовании предло-

женного подхода возникает вопрос о достоверности принимаемых решений. Вероятность в модели (4) является монотонно возрастающей функцией величины 9—р. Таким образом, нижняя доверительная граница оценки этой вероятности по частоте соответствует нижней доверительной границе косвенного измерения 9—р. В результате приходим к простой практической методике учета погрешностей при замене истинного значения вероятности P его оценкой

1,099 - 0,733

= 0,916 и прогнозируемых чис

ло циклов для достижения PH = 0,999999 бу-13,8 -1,832 _ дет пс =             ” 13, т.е. уже погрешности в 0,916

А

P

M

= —, показанной ниже на конкретном примере.

оценок P уже существенно влияют на количество циклов обучения.

Для сокращения необходимого числа циклов обучения необходимо повысить его эффективность.

Пример 5. Пусть в результате ознакомительного тестирования 10 обучающихся по 10 кон-

трольным вопросам ( N = n • к = 10 40 = 100) по-

Пример 6. Пусть при остальных условиях примера 5 число правильных ответов после 2-ого цикла обучения повысилось до 95. Тогда P = 0,95 , нижняя доверительная граница составит

лучено 80 правильных ответов, т.е. P =

-8» = 0,8.

100      .

P h = 0,95 - 1,28

Используя нормальную аппроксимацию би-

1 0,95 • 0,05

~ 0,922 ,

номиального распределения, получим нижнюю

90% доверительную границу при у = 0,9:

А

P H = P - u l - /

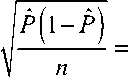
откуда

0 922    0 75

0₂ - р₂ = In⁰⁹--In⁰⁷⁵ = 2,47 - 1,099 = 1,371 .

²          0,078    0,25

Средний темп роста будет

1,099 - 1,371 = _{1 23}5

2,

0,8 - 1,28

1 0,8 • 0,2

» 0,75 ,

и потребуется п _в =

13,8 - 2,47

1,235

- 9,

т.е. повыше-

где u _x__Y - квантиль стандартного нормального распределения.

Далее расчет проводится аналогично при, 0,75 n п , меру 3, т.е. In о 25 = ^ - Р1 = 1,099, и верхнее

ние эффективности обучение на 5% приводит к снижению объема обучения более чем на 30%.

Таким образом, разработанная методика позволяет планировать и управлять многоэтапным процессом обучения, что обеспечивает его эффективность.

значение числа циклов п_в

13,8 - 1,832 0,916

При этом прогнозируемое значение после

2-ого цикла обучения составит ln— = 1,099 • 2 , q ₂

откуда р ₂ = 0,9 .

ЗАКЛЮЧЕНИЕ

В отличие от традиционных моделей двухфакторного дисперсионного анализа модель Г. Раша позволяет не только оценить влияние факторов сложности, но и рассчитать вероят- ность успешного обучения как в дискретной, так и в непрерывной шкалах, провести прогноз и планировать число циклов обучения, что не- 3.

возможно при использовании традиционных моделей дисперсионного анализа. Эта особенность предложенного подхода в значительной 4. степени помогает оценить и проанализировать процесс подготовки специалистов в области эксплуатации авиационных и космических систем в динамике, предоставляя информацию для своевременной коллекции процесса обучения и 5.

выработки наиболее оптимальных решений.