Сравнительный анализ методов определения спектральной плотности мощности по ортогональной модели структурной функции

Самарский государственный аэрокосмический университет

Спектральная плотность мощности является одной из распространенных характеристик в анализе случайных процессов и существует множество способов ее определения. В данной работе рассматриваются особенности определения спектра по ортогональной модели структурной функции в случае стационарности исследуемого процесса, а также когда рассматривается случайный процесс со стационарными приращениями.

Обработка случайных процессов (СП) во многих случаях требует определения спектра. Это относится как к стационарным (ССП), так и к нестационарным процессам (НСП). В случае стационарных процессов справедливо следующее выражение, связывающее корреляционную (КФ) и структурную функции (СФ) процесса [1]:

K x (т ) = - 1 [ S , ( Т ) - S , ( « ) ] . (1)

Необходимо отметить, что правая часть выражения (1) содержит уменьшенную в два раза и центрированную относительно значения в бесконечности структурную функцию (ЦСФ). Подставляя выражение (1) в формулу Винера-Хинчина [2], можно определить спектральную плотность мощности (СПМ) следующим образом:

1 7° g,(®) = -? f Sx (т)cos(®T )dT ,   (2)

2π 0

где S x (T ) = S , (T ) - S , ( 7 ).

Представляя модель ЦСФ в виде [3]

^Sa ^{( T}) = Z ^в к У к ^{( T , a} ),        (3)

к =0

где m – число членов разложения ряда;

β_k – коэффициенты разложения;

ψ_k ( τ , α ) – семейство ортогональных функций ( α – параметр масштаба ортогональных функций), выражение (2) примет вид

1 ^{m 7}

g,®)= , Z в f^k (t)cos(®T) dT =

2п k =o ^J₀ ^m                               , (4)

= -V Z в к Re W k ( j® )

2n Я

где Re W_k ( jω ) – вещественная часть частотной характеристики ортогональных фильтров [4].

В табл. 1 представлены выражения для определения СПМ в ортогональных базисах Лагерра, Лежандра и Дирихле.

Но выражение (4) позволяет определять СПМ только в случае стационарности СП, хотя структурная функция чаще является характеристикой случайных процессов со стационарными приращениями (СПСП), которые классифицируются, как вид НСП. Это

Таблица 1. СПМ в случае CСП

О S cd и gx(ω) ϕ cd (D cd 4 - cos^ IL (-1)k вк ■ па k=o • cos[(2 к +1)^] arctg( A), 2ω A = — α cd s 1mβ Z ” • cos Фк • 2па   2к +1 к = o • cos Фк + 2L Фs L         s=o J Ф n = arctg( An), A„ =---®--- (2 n + 1)а (D к к -    £ (-1) к     COS ф • 2па tO,     к +1 • cos Фк + 2к>1 Фs L         s=o    J Фn = arctg(An ) , A = —®— (n + 1)а обстоятельство предполагает несколько иное определение СПМ [1]:

1 ГО                  ° gx (Ю) = ~---fSln( ®Т ) S' x (т)dт   (5)

2 πω ₀

°

;, ,.   aSx(т )

где S' x (т) =----— дт

.

После математических преобразований выражение (5) примет вид [3]

1m k gx(а)э ЕekЕAk,s(а) • Bs(a,®). (6) 2п к =0 s=0

A_{k , s} ( α ) и B_s ( α , ω ) для различных базисов представлены в табл. 2.

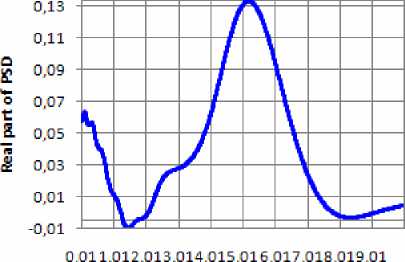
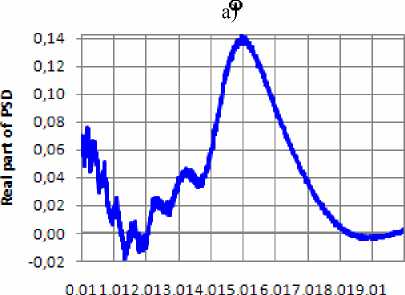
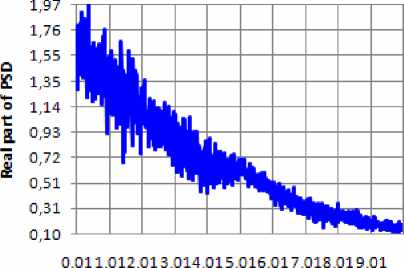
Определение СПМ с помощью выражения (6) влечет за собой определенные ограничения на его использование: в состав этого выражения входят коэффициенты A_{k , s} ( α ), которые представляют собой алгебраические действия с факториалами чисел, пропорциональных числу членов разложения ряда (3). Таким образом, при относительно небольшом m (для функций Лагерра это число равно 2022 члена), во время вычисления A_{k , s} ( α ) происходит переполнение мантиссы числа, что приводит к некорректным результатам вычисления СПМ (рис. 1).

К определению выражения (5) можно

б)

в)

Рис. 1. СПМ при использовании выражения, содержащего факториалы: а) относительная погрешность аппроксимации ЦСФ 5 =0,079; m=19; базис:Лагерра;

б) относительная погрешность аппроксимации ЦСФ 5 =0,067; m=22; базис:Лагерра;

в) относительная погрешность аппроксимации ЦСФ 5 =0,061; m=24; базис:Лагерра

Таблица 2. Коэффициенты для СПМ

О S 1-9	A k , s ( α )	B s ( α , ω )
cd о cd ч	( — 1) s a s • k ! ( к — s )!( s !)2	s !cos s ( ф )r . / x vs /[ sin ( s • ф ) [ a ] ® l      1 1 2 J — sln ( ( s + 1) ф ) • cos ( ф ) ] , . Г 2ю ) где ф = arctgl — 1 V a J
cd Et S cd S о ч	( — 1) s +1 (2 s + 1) a ^ ( к + s )! ( к — s )!( s !) 2	1 (2 s + 1) 2 a 2 + to1
о ч X S S	( — 1) к — s +1 ( s + 1) a ^ ( к + s + 1)! ( к — s )!( s + 1)! s !	1 ( s + 1)2 a 2 + to ^

также применить иной подход. Применяя формула Эйлера и учитывая, что

д Lag к ( т , а )

д т

k

= Е С к ( — а ) ‘ 1 • s !

s =0

•

— ат s^—1 e 2

—

α 2 τ^se

ατ

,

где Lag_k ( τ , α ) – ортогональная функция Ла-герра k-го порядка;

выражение (5) легко представить в виде

°

S a ( τ )

а)

Выполнив простейшие алгебраические преобразования и используя формулу бинома Ньютона, конечное выражение будет иметь вид

g x И =

cos ϕ πα

m

£ (-1)k+1 вк к=0

cos ^{[ (} 2 к + 1) ^ ] , (9)

. I 2™ I где ф = arctgl I. V a ;

g _x ( ω )

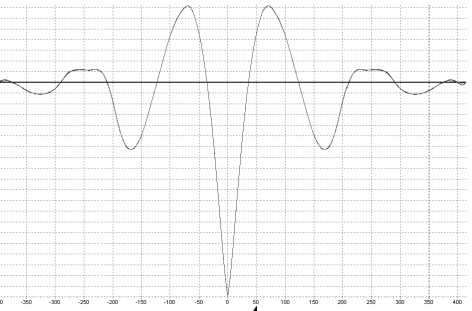
Полученное выражение может применяться для СПСП и не ограничивается числом членов разложения ряда ЦСФ. Пример использования выражения (9) приведен на рис. 2.

ω

б)

Рис. 2 . Пример определения СПМ без ограничений на модель ЦСФ:

а) ЦСФ и ее модель. 5 =0,0003; m=170; базис:Лагерра; б) СПМ, полученная по модели СПМ

g_x ( ω )

4 jωπ

mk

£ в к £ C( - a s • к = 0      s = 0

/г

α

•

-

!( a + j™ ) s   ⁽ a + j® ) s ^{+ 1}

-

-

-

α

\

(1 - j™)s  (1 - И) s+1