Сравнительный анализ нейросетевых и ARIMA-моделей для прогнозирования временных рядов: оценка эффективности и применимости

Прогнозирование временных рядов имеет решающее значение во многих областях, включая финансы, экономику и здравоохранение. Оно позволяет организациям и исследователям делать обоснованные прогнозы на основе исторических данных. Существует

Сравнительный анализ нейросетевых и ARIMA-моделей для прогнозирования ...

Раскатова Марина Викторовна кандидат технических наук, доцент кафедры информационных технологий и естественнонаучных дисциплин, Национальный исследовательский университет «МЭИ», Москва. Сфера научных интересов: нейронные сети, вычислительная техника, прогнозирование временных рядов, сравнительный анализ моделей прогнозирования. Автор более 100 опубликованных научных работ. ORCID: 0000-0001-7671-3312, SPIN-код: 8053-5041, AuthorID: 609945.

множество различных методов прогнозирования временных рядов, каждый со своими преимуществами и недостатками. В статье сравнивается точность прогнозов двух моделей на основе ряда метрик, включая среднюю абсолютную ошибку.

ARIMA-модели

ARIMA – интегрированная модель и методология анализа временных рядов. Для прогнозирования временных рядов ARIMA использует интегрированную модель авторегрессии – скользящего среднего. Есть три различных числа (p, d, q), которые используются для параметризации моделей в ARIMA. В связи с этим модели ARIMA обозначаются символом ARIMA (p, d, q). Вместе эти параметры подсчитывают сезонность, тенденцию и шум в наборах данных:

p – это авторегрессионная модель. Модель временных рядов, в которой значения временного ряда в данный момент линейно зависят от предыдущих значений этого же ряда;

d – интегрированная часть модели;

q – скользящая средняя модели. Именно она позволяет установить погрешность модели как линейную комбинацию значений ошибок, которые произошли в прошлом.

Для сезонного прогнозирования временных рядов можно предложить удачный вариант модели ARIMA – сезонный вариант SARIMA или SARIMAX. В этой модели сезонная дифференциация соответствующего порядка используется для удаления нестационарно-сти из ряда [1; 2].

Нейросетевые модели

Функция искусственной нейронной сети состоит в том, чтобы отобразить множество входов на множестве выходов. В начальный период на некотором множестве пар «вход – выход» происходит обучение нейросети. В основе нейросети лежит искусственный нейрон.

На Рисунке 1 представлена схема произвольной искусственной нейронной сети.

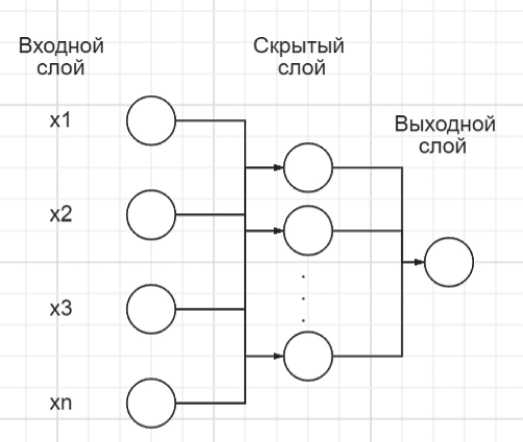
Рисунок 1. Схема ИНС

Источник: здесь и далее схемы, рисунки и графики составлены авторами.

Л.Г. Комарцова и А.В. Максимов подчеркивают, что «искусственный нейрон – это узел искусственной нейронной сети, являющийся упрощенной моделью естественного нейрона» [3, с. 40].

Существуют следующие типы нейронных сетей.

• 1.    «Персептрон – первая модель обучения с учителем. Обучение персептрона требует наличие учителя и состоит в таком подборе весов w_ij , чтобы выходной сигнал iy был наиболее близок к заданному значению d_i . При таком способе обучения каждой обучающей выборке, представленной вектором x, поставлено в соответствии ожидаемое значение d_i на выходе i -го нейрона» [4, с. 11].

• 2.    «Многослойные персептроны (MLP) – это нейронная сеть, состоящая из входного, выходного и расположенных между ними одного (или нескольких) скрытых слоев нейронов» [5, с. 25].

• 3.    «Рекуррентные нейронные сети (RNN) являются наиболее подходящими для анализа последовательных данных, таких как язык. В рекуррентных нейронных сетях невозможно выделить отдельные слои. Сигналы могут циркулировать по сети во всех направлениях, образуя сложную пространственно-временную структуру (pattern)» [6, с. 61].

• 4.    «Сверточные нейронные сети (CNN) являются одной из форм многослойных нейронных сетей. Первая часть состоит из слоев свертки и максимального пула, которые выступают в качестве экстрактора признаков. Вторая часть состоит из полносвязного слоя, который выполняет нелинейные преобразования извлеченных признаков и действует как классификатор» [7, с. 10].

• 5.    «Глубокие нейронные сети (DNN) – сети с большим числом слоев для автоматического извлечения признаков из сложных данных» [8].

Сравнительный анализ нейросетевых и ARIMA-моделей для прогнозирования ...

Прогнозирование временных рядов с трендом при помощи ARIMA-модели и нейросетевой модели

Для проведения сравнения ARIMA-модели и нейросетевой модели в данном исследовании использовалась программа STATISTICA. Экспериментальные данные, касающиеся количества продаж малого бизнеса, были занесены в программу STATISTICA с целью прогнозирования будущего количества продаж. Количество данных составило: 55 значений для обучающей выборки и 10 значений для тестовой выборки. Для этой цели был построен линейный график данных (см. Рисунок 2), демонстрирующий предполагаемое наличие тренда и нестационарность ряда.

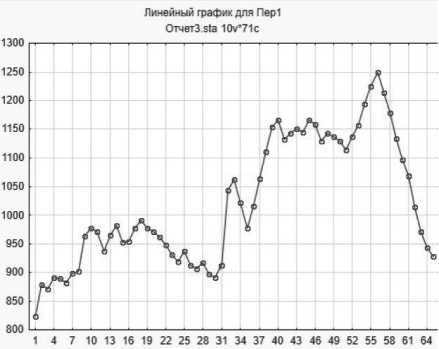
Рисунок 2. Линейный график временного ряда

Для подтверждения этого предположения был использован тест Дики – Фуллера [9], выполненный при помощи языка программирования PYTHON, результаты которого показали, что ряд является нестационарным. Для достижения стационарности временного ряда было проведено интегрирование.

На Рисунке 3 можно увидеть продифференцированный линейный график временного ряда.

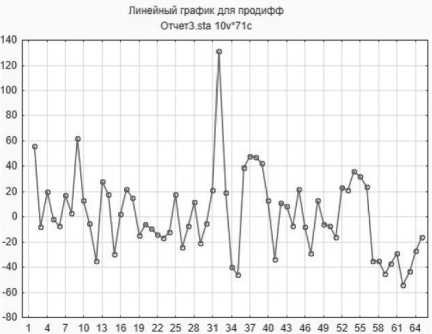
Рисунок 3 . Продифференцированный линейный график временного ряда

Затем была построена автокорреляционная функция (далее – АКФ) [10] и частичная автокорреляционная функция (далее – ЧАКФ), на основе которых были определены параметры ARIMA-модели: p = 1, d = 1, q = 1 [11].

После подбора параметров был построен прогноз по всей модели (см. Рисунок 4) и проведен анализ ее адекватности с использованием трех методов: визуального анализа, оценки гистограммы остатков и расчета средней абсолютной ошибки MAPE, задаваемой формулой

( v, - v₃ )

MAPE = abs 1--2 -100% , v1

где v ₁ – фактические данные; v ₂ – прогнозируемые данные.

Гистограмма остатков показала нормальное распределение, ошибка MAPE составила 3,112 %, что свидетельствует о том, что модель адекватна.

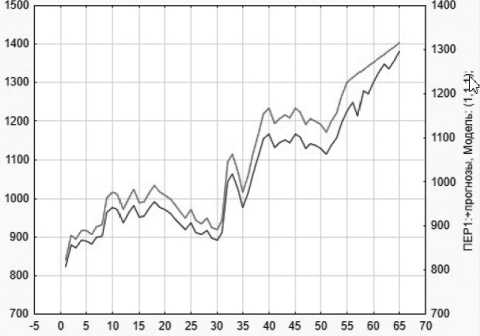
Рисунок 4. Прогноз по всей модели

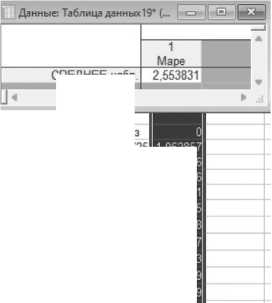
После проверки модели на адекватность можно построить прогноз на тестовой выборке для 10 значений. Ошибка MAPE методом построения прогноза ARIMA-модели составила 2,554 % (см. Рисунок 5).

СРЕДНЕЕ набл

1279.000

1271,000

1303,000

1367,000

1380,000

1 062857 2 492336

2 024326 0,714861

2 476885 3,503978 4 496037 2.834483 3.760439 4 725939

1326.000

1349.000

1335,000

прогноз 1235,7251

1244,257 1253,109

1261,914 1270,726

1279,537 1288,348

1297,160 1305,971

1314 782

нач дан i 1249.000 1214.000

Рисунок 5. Ошибка MAPE методом построения прогноза ARIMA-модели

Сравнительный анализ нейросетевых и ARIMA-моделей для прогнозирования ...

Для создания прогноза временных рядов с использованием нейросетевой модели был задействован пакет «Автоматизированная нейронная сеть» в программе STATISTICA. При использовании тех же данных (55 для обучающей выборки и 10 для тестовой) было построено 5 нейросетевых моделей: MLP 12–4–1, MLP 12–4–1, MLP 12–2–1, MLP 12– 3–1, MLP 12–4–1, указанных на Рисунке 6.

Активные сети

СетьЮ	Архитектура	Произвол	Контр, и..	Тест, произ...	Алгоритм	Функ. о...	Акт. скры.	Акт. вых...
1	MILP 12.4-1	0,913565	0,848776	—	BFQS 12	Сум. ква...	Логистиче...	Тождест...
2	MLP 12-4-11	0,911373	0.847955	...	BFQS 9	Сум, ква,.	Гиперболи.	Т ождест...
3	MLP 12-2-11	0,904971	0,855574	—	BFQS 9	Сум. ква...	Гиперболи, ,	Тождест,,.
4	MLP 12-3-11	0,947144	0.880969	—	BFQS 72	Сум. ква...	Гиперболи...	Т ождест...
R	Ml IP117.ЛЛ	n 417484	n №7747		PFR^ 11	F^lkA v©.&	П ГХ-Ц«-*Г1 Л .6	Т о'*,Аа*^т

Рисунок 6 . Построенные сети

Для оценки качества этих моделей были проанализированы гистограммы остатков и проведено сравнение их прогнозов для временного ряда (см. Рисунок 7). Анализ гистограмм остатков важен для определения соответствия модели предположениям о нормальности распределения остатков. Сравнение гистограмм помогает выявить различия в точности прогнозов, а также возможные проблемы в моделях.

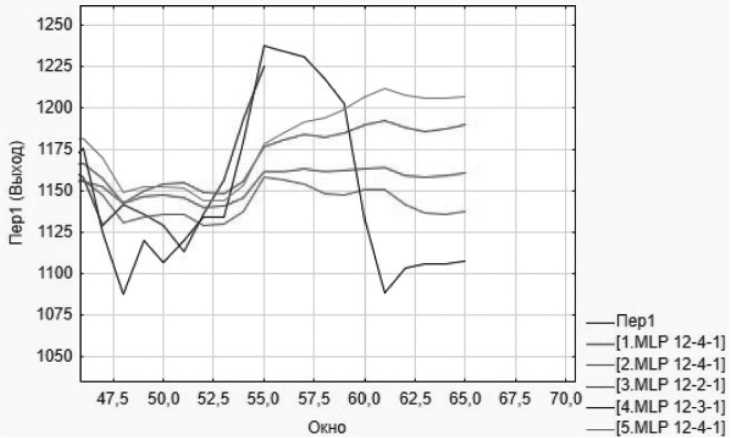
Рисунок 7. Прогноз исходного ряда пятью нейросетевыми моделями

После анализа гистограмм и прогноза моделей была выявлена наиболее подходящая нейросетевая модель (MLP 12–3–1), с помощью которой была оценена ошибка MAPE для тестовой выборки – она составила 10,76 % (см. Рисунок 8).

Рисунок 8. Ошибка MAPE для тестовой выборки Прогнозирование временных рядов с факторами при помощи ARIMA-модели и нейросетевой модели

Медведева Н.И. утверждает, что «факторы – это те процессы, которые существенным образом могут повлиять на дальнейшее развитие событий и их конечный результат, поэтому они должны учитываться в прогнозах.

При разработке прогнозов важно обозначить, какие факторы признаются неизменными в будущем, а какие изменяются и включаются в варианты прогноза» [12, с. 405].

Для прогнозирования количества продаж можно взять те же данные со следующими факторами: «количество рабочих дней», «приток новых клиентов», «затраты на рекламу». Эти факторы являются изменяемыми.

ARIMA-модель не включает в себя учет влияющих факторов на конечную переменную. Она применяется для анализа и прогнозирования временных рядов и фокусируется на авторегрессии, интеграции и скользящем среднем значении [13]. Поэтому в исследовании не учитываются факторы, описанные ранее. Так, ошибка MAPE составила 2,554 % (как и в прогнозировании временных рядов с трендом) .

В прогнозировании нейросетевым пакетом использовались упомянутые ранее факторы, которые представлены на Рисунке 9.

W Выберите переменные для анализа

2■Пер2

• 3    • количество рабе»

• 4    - приток НОВЫХ КЛ1

• 5    - затраты на реклг

• 6    - Перб

7-Пер7

• 8    -Пер8

• 9    -Пер9

• 10    - кол-во рабочих

• 11 - ППИТОК НОВЫХ KI

6 - Перб 7-Пер7 8 -Пер8 9 - Пер9

13-НовПерЗ

14 - НовПер4

15 - НовПерБ

• 1    - кол-во продаж

• 2    -Пер2

• 3    - количество рабо* 4 - ПРИТОК НОВЫХ КЛ1 5 - затраты на реклг 6 - Перб 7-Пер7

8-Пер8 9-Пер9 10 - кол-во рабочих

11- ПЛИТОК НОВЫХ KI

[Наборы]...

Используйте опцию Подходящие переменные" для предварительного

Подробно Инфо Подробно Инфо

Непрерывная целевая Непрерывная входная

Подробно Инфо

Категриальная входная

категориальных и негрерывных

Нажмите F1 для

10-12

справки.

О Подходящие переменные

Рисунок 9. Факторы, используемые при прогнозировании

Воспользовавшись методом многократных подвыборок, было построено n количество нейросетевых моделей. После обучения этих сетей было выявлено, что три из них имеют

Сравнительный анализ нейросетевых и ARIMA-моделей для прогнозирования ...

самый лучший результат: контрольная производительность и тестовая производительность близки к 1. На Рисунке 10 показаны выявленные три модели: MLP 36–30–1, MLP 36–20–1, MLP 36–10–1.

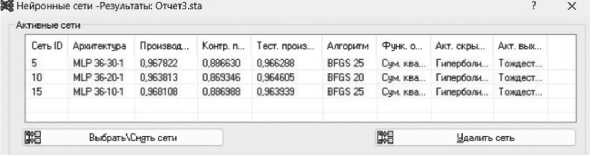
Рисунок 10. Наиболее подходящие модели по контрольной и тестовой производительности

Проанализировав гистограмму остатков, ошибку MAPE и прогнозирование исходного временного ряда, можно сделать вывод, что модель MLP 36–30–1 считается наиболее подходящей.

Модель MLP 36–30–1 на проекции исходного ряда можно увидеть на Рисунке 11.

Ошибка MAPE этой модели составила 1, 374 %, что представлено на Рисунке 12.

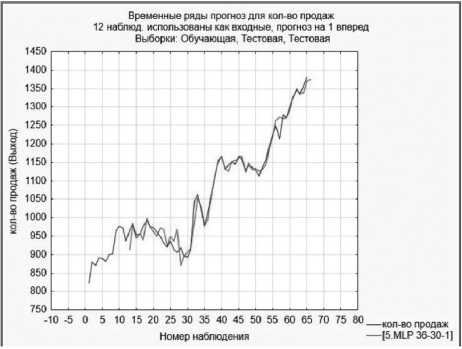
Рисунок 11 . Модель MLP 36–30–1 на проекции исходного временного ряда

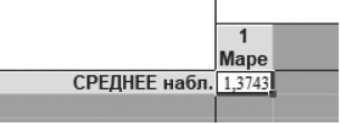
Рисунок 12. Ошибка MAPE для модели MLP 36–30–1

Заключение

Таким образом, в результате исследования можно сделать вывод, что ARIMA-модель лучше всего подходит для данных, которые являются стационарными либо имеют тренд. Также ARIMA-модели хорошо работают с данными, которые имеют сезонность, например, ежедневными или ежемесячными данными.

Нейросетевые модели лучше всего подходят для данных, которые являются нестационарными, имеют сложную зависимость между переменными, имеют факторы, влияющие

на прогноз. Они также хорошо работают с данными, которые имеют высокую размерность или содержат пропуски или выбросы.

Этот вывод может быть полезен при выборе метода прогнозирования исходя из специфики данных и задачи исследования.

Также в качестве итога можно отметить, что вместо использования ARIMA-моделей при прогнозировании данных, имеющих факторы или сезонность, лучше использовать модель SARIMA или SARIMAX.