Сравнительный анализ некоторых алгоритмов демодуляции в каналах с межсимвольной интерференцией

Существенная часть каналов связи, используемых в настоящее время для передачи дискретных сообщений, относится к классу каналов с межсимвольной интерференцией, под которой мы будем понимать нарушение взаимной ортого- нальности между элементами принимаемой сигнальной последовательности:

( ф ( t ) , ф ( t - k • T ) ) * 0; k = ± 1, ± 2, ± 3.. , (1) где ф ( t ) - вектор-функция элемента принимаемой сигнальной последовательности, (,) - знак скалярного произведения в гильбертовом или евклидовом пространстве.

Одной из наиболее распространённых причин возникновения МСИ является многолучевое (многопутевое) прохождение сигнала в среде распространения [1,2].

К каналам такого типа следует отнести радиолинии коротковолнового (декаметрового) диапазона, каналы мобильной связи, тропосферные линии связи и т.д.

Основные методы демодуляции сигнальных последовательностей в каналах с МСИ

В настоящее время разработаны разнообразные варианты демодуляторов, предназначенных для работы в каналах с межсимвольной интерференцией. Наилучшую помехоустойчивость при обработке сигнальных последовательностей на выходе каналов с МСИ обеспечивают оптимальные нелинейные демодуляторы [1,3], минимизирующие среднюю вероятность ошибки на символ. В этом случае функцию правдоподобия для фиксированной позиции демодулируемого сигнального элемента, в соответствии с известной формулой полной вероятности, можно представить в виде суммы условных функций распределения, соответствующих всем возможным вариантам вектора сопровождающих сигнальных элементов. Тогда соответствующее решающее правило при равновероятных символах, определяющих сигнальную последовательность, можно представить следующим образом:

ледовательности сопровождающих символов B i = B ^{( k} ) .

Если к (2) применить правило обобщенного максимального правдоподобия [1], суть которого заключается в выделении максимального слагае- мого в сумме условных функций распределения, то данное решающее правило можно преобразо- вать следующим образом:

m i = arg max m

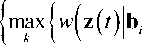
= b ^{( m )} ; B i = B ^{( k} ) ) } } (3)

Как показано в [3,4] демодуляторы на основе решающего правила (3) несущественно уступают демодулятору (2), оптимальному с точки зрения критерия минимума вероятности ошибки на сим- вол, и являются асимптотически оптимальными при увеличении отношения сигнал/шум.

При АБГШ на выходе канала связи решающее правило (2) сводится к сравнению гильбертовых метрик, вычисляемых на некотором интервале анализа TA с учётом действия всех сигнальных составляющих:

= arg max m

m i = arg max m

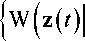
bi = b(m‘)} =

m i

J

= argmin < min < V [I z j ( t ) -s j ( t ; b i^{m )} , B i ) ) ) mk  ^jj

⎪_⎩         ⎪⎩ j=1 T _A

dt

A

⎧⎪ ^ML

iS w (z (t) b

⎪⎩ k=1

=b(m); Bi = B(k)

= arg min { min { |z ( t ) - s ( t; b , _m , B_ik

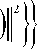
где z ( t ) - вектор-функция сигнала на входе демодулятора, включающая в себя, в обще м слу чае, J сигнальных составляющих; i е 0; I - 1 – номер демодулируемого сигнального элемента в принимаемой последовательности; I – длина принимаемой последовательности (пакета); T – тактовый интервал; b _i – двумерный вектор амплитуды демо дулируемого сигнального элемента; m eG; M -1 - один из возможных номеров позиции демодулируемого сигнального элемента; m i –решение относительно номера позиции демодулируемого сигнального элемента; M – позиционность используемой сигнальной системы; B i = [ b 1 b ₂ .. b i_ , b _{i + 1} .. b I ] - вектор амплитуд сопровождающих сигнальных элементов (как предшествующих де модули руемому, так и последующих за ним); к е 1; M I^{- 1} - номер варианта вектора сопровождающих символов; W ( z ( t ) |b i = b ^{( m )} ) - условная функция распределения (функция правдоподобия) вектор-функции сигнала на входе демодулятора z ( t ) при фиксированном варианте демодулируемого символа b i = b ^{( m )} ; w ( z ( t ) |b i = b ^{( m )} ; B i = B ^{( k )} ) - условные функции распределения указанного вектора при фиксированных вариантах амплитуды демоду- b(m)

i ⁼b и пос-

Естественно, что при существенной длине сигнального пакета реализация алгоритма (4) наталкивается на непреодолимые трудности. В ряде публикаций[1,2]рекомендуетсяограничитьвели-чину T_A интервалом временного рассеяния демо-дулируемого сигнального элемента ( Q + 1 ) - T , поскольку в данном временном интервале содержится вся энергия этого элемента.

Наряду с решающими правилами, оптимальными или субоптимальными по критерию минимума вероятности ошибки на один бит, нашли применение демодуляторы, минимизирующие вероятность ошибки сигнальной последовательности. В этом случае оптимальное решающее правило можно представить следующим образом:

k = max { w ( z ( t ) |B ^{( k} ) ) } ; k e l; M I (5) где k e l, M I - номер одной из возможных последовательностей сигнальных элементов; B ^{( k} ) =|^ b ^{( k} ) b ⁽ ₂k ) .. b lk ) J - вектор, включающий в себя амплитуды всех элементов сигнальной последовательности с номером k ; k - реше-ние,принятоеотносительнономерапринимаемой сигнальной последовательности.

При наличии АБГШ в канале связи соответствующий алгоритм демодуляции можно представить в виде:

⎪ k = min <

k

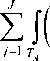
z ■ j ( t ) - s j ( t ; B ^{( k} ' ) ) 2

dt > ;

где T_A равен длительности всего сигнального пакета с учётом временного рассеяния в канале.

Среди алгоритмов, минимизирующих вероятность ошибки при приёме сигнальной последовательности, следует отметить алгоритм Витерби (АВ), первоначально применявшийся для декодирования свёрточных кодов. При неограниченном увеличении задержки в принятии решения (вплоть до конца сигнального пакета) данный алгоритм является оптимальным, и эквивалентен приёму в целом всей сигнальной последовательности. Отметим, что вычислительная сложность АВ существенно меньше по сравнению с «лобовым» алгоритмом типа (6), и пропорциональна величине I M ^Q .

Рассмотренные алгоритмы демодуляции являются субоптимальными для каналов связи с сильно выраженной МСИ, однако их практическое применение в ряде случаев наталкивается на существенные реализационные трудности. Это объясняется тем, что их вычислительная сложность возрастает по показательному закону как при увеличении позиционности сигнальной системы, так и при увеличении интервала временного рассеяния единичного элемента принимаемого сигнала.

В силу этих причин представляют интерес демодуляторы, синтезированные на основе методов линейной коррекции (линейные выравниватели) [6,7], достоинством которых является относительно невысокая вычислительная сложность, возрастающая по линейному закону при возрастании относительной памяти канала, и не зависящая от позиционности сигнальной системы.

Еще в 1965 г. Тафтсом было показано [7], что оптимальная структура выравнивателя применительно к различным критериям оптимизации представляет собой каскадное соединение фильтра, согласованного с единичным элементом принимаемого сигнала (СФ) и выравнивающего фильтра (ВФ), который, как правило, представляет собой трансверсальный фильтр конечной длины, задержка между отводами которого определяется тактовым интервалом T .

Отсчет сигнала на выходе выравнивающего фильтра (ВФ) определяется как скалярное произведение вектора отсчетов принимаемой смеси с выхода СФ и вектора весовых элементов:

X = y ' x 0 ,                  (7)

где i определяет номер сигнального элемента, y i = [ y_t - L + 1 .. y_w y, У + 1 .. У + L - 1 ] ^- со ответствующий вектор отсчётов с выхода ВФ; ®' = [ 9 - L + 1 .. 9 - 1 0 0 0 1 .. O l - 1 ] ^— вектор весовых элементов выравнивающего фильтра; _' – символ транспонирования.

В геометрическом плане процедура выравнивания сводится к вычислению проекции принимаемой сигнальной последовательности на направление вектора весовых элементов ВФ, который выбирается в соответствии с некоторым критерием оптимизации.

Наиболее широкое применение в этом плане нашли ВФ, отводы которых оптимизированы в соответствии с критерием минимума среднеквадратического отклонения (СКО) [6].

В соответствии с данным критерием должен минимизироваться средний квадрат погрешности оценки амплитуды демодулируемого сигнального элемента на выходе выравнивающего фильтра:

£ ² = E { ( b i - b i ) } (8)

Кроме того, в технике связи нашли применение выравниватели на основе так называемого E - критерия, который предусматривает минимизацию остаточной МСИ, без учёта влиянии аддитивной помехи [8-9].

Особенностью демодуляторов обоего типа является то, что при их использовании принятие решения о некотором символе осуществляется на основе соответствующего фрагмента принимаемого сигнального пакета, который включает в себя сигналы сигнальных элементов, как предшествующих демодулируемому, так и последующих за ним.

Применение обратной связи по решению (ОСР) [1; 9-10], которая предполагает вычитание последействий от сигнальных элементов, предшествующих демодулируемому, позволяет существенно упростить переборный процесс при использовании алгоритма (4) (число перебираемых альтернатив сокращается M^Q раз), а при использовании линейного выравнивателя длина выравнивающего фильтра уменьшается вдвое.

Отметим, что в обоих случаях существенно улучшается помехоустойчивость системы несмотря на эффект размножения ошибок [6].

Алгоритм (4) при использовании ОСР получил название «алгоритма приема в целом с поэлементным принятием решения» или алгоритма Кловского-Николаева (АКН) [1-2].

Особенностью данного алгоритма является то, что вероятность ошибки при демодуляции каждого сигнального элемента в существенной сте- пени зависит от сопровождающих сигнальных элементов, следующих за ним. При этом следует отметить т.н. «вырожденные комбинации», обладающие наихудшей помехоустойчивостью, и которые в значительной мере определяют среднюю вероятность ошибки на бит [2].

В свою очередь, при использовании выравнивателя с ОСР (ВОСР) сопровождающие сигнальные элементы практически не оказывают влияния на демодуляцию. Наличие ошибок в данном случае определяется взвешенной суммой отсчётов аддитивного шума, поступающих с отводов линии задержки ВФ.

Таким образом, ошибки при демодуляции в соответствии с АКН, и при использовании ВОСР в значительной степени обусловлены различными физическими факторами. Это обстоятельство позволяет сделать вывод о том, что значительная часть ошибок, возникающих при работе указанных демодуляторов не совпадает, что подтверждается результатами эксперимента, которые представлены в следующем разделе.

Анализ характеристик и выводы

На рис.1 и рис.2 представлены вероятностные характеристики демодуляторов различного типа при работе в каналах с МСИ, обусловленной многолучевым распространением сигналов, полученные методом имитационного моделирования при удельной скорости модуляции ( Бод/Гц).

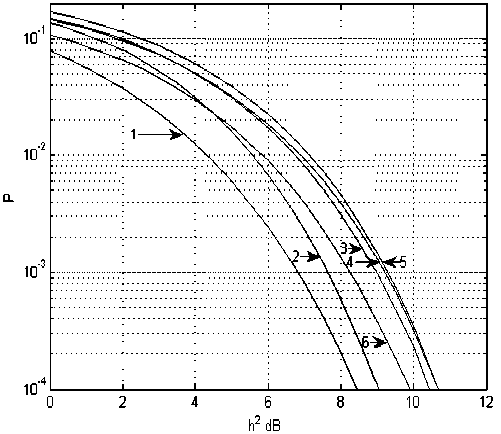
Рис. 1 Характеристики помехоустойчивости при работе в двухлучевом канале связи с фиксированными параметрами (J = 1, LP = 2, Y1 = Y2,t2-T1 = 1.5-T ): 1 — прием одиночных сигнальных элементов (отсутствие МСИ); 2 – демодуляция сигнального пакета по алгоритму Витерби с задержкой в принятии решения, равной длине пакета (прием в целом); 3 – демо- дуляция сигнального пакета в соответствии с АКН; 4 – демодуляция сигнального пакета выравниванием с ОСР по критерию минимума СКО; 5 – демодуляция сигнального пакета выравниванием с ОСР по E-критерию; 6 – кривая совпадающих ошибок при демодуляции сигнального пакета в соответствии с АКН и ВОСР

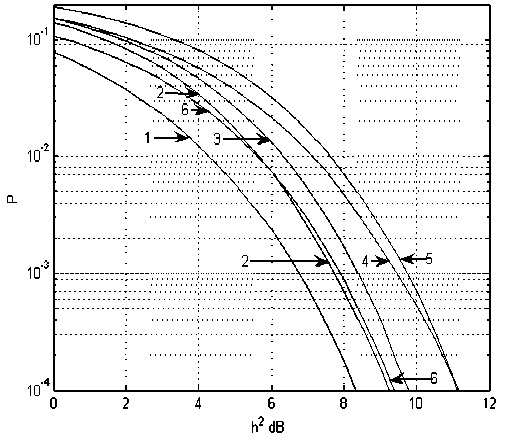
Рис.2 Характеристики помехоустойчивости при работе в трёхлучевом канале связи с фиксированными параметрами (( J = 1; L P = 2 Y 1 = 1,Y 2 =^- 1,Y₃ = 0,6, т 2 - T 1 = 1,5 • T , т 3 - T 1 = 3,5 • T ): 1 - прием одиночных сигнальных элементов (отсутствие МСИ); 2 – демодуляция сигнального пакета по алгоритму Витерби с задержкой в принятии решения, равной длине пакета (приём в целом); 3 – демодуляция сигнального пакета в соответствии с АКН; 4 – демодуляция сигнального пакета выравниванием с ОСР по критерию минимума СКО; 5 – демодуляция сигнального пакета выравниванием с ОСР по E -критерию; 6 – кривая совпадающих ошибок при демодуляции сигнального пакета в соответствии с АКН и ВОСР

Из приведенных результатов следует, что все алгоритмы демодуляции существенно проигрывают потенциальной кривой, соответствующей оптимальной демодуляции в отсутствие МСИ.

Наилучшую помехоустойчивость из представленных алгоритмов демодуляции сигнальных последовательностей при наличии МСИ обеспечивает алгоритм Витерби с задержкой, равной длине сигнального пакета, эквивалентный приёму в целом всей сигнальной последовательности.

Рассматривая алгоритмы поэлементной демодуляции, следует отметить, что переборный алгоритм с ОСР (АКН) обеспечивает несколько лучшие результаты, чем выравниватель с ОСР, причём в каналах с сильно выраженной МСИ выигрыш становится более существенным.

При этом интервал анализа для АКН предполагался равным интервалу рассеяния единичного сигнального элемента T A = ( Q + 1 ) • T , а длина выравнивающего фильтра (т.е. число отводов) составляла величину L = 3 • ( Q + 1 ) .

Выравниватель с ОСР на основе E -критерия уступает соответствующему выравнивателю, оптимальному по критерию минимума СКО, причём энергетический проигрыш имеет тенденцию к уменьшению при увеличении отношения сиг-нал/шум).

Особый интерес представляет собой кривая 6, из анализа которой следует, что доля совпадающих ошибок при использовании АКН и ВОСР относительно невелика, что, в принципе, дает возможность разнесения по алгоритмам демодуляции.