Сравнительный анализ процедуры фазирования псевдослучайной последовательности на каналах с зависимыми и независимыми ошибками

Предположим, что параметр релеевского канала не успевает измениться на заданном интервале времени, то есть: μ1 = μ2 =...= μn = μ... Указанные каналы называются составными каналами с переменными параметрами (КПП) [1]. Такие условия приближенно выполняются, например, для коротковолновых (КВ) каналов, если n·τ0 ≤ 0,5 c, а для тропосферных каналов при условии n·τ0 ≤ 0,05 c. Соответственно с учетом скорости передачи по данным каналам получим для КВ-канала n ≤ 0,5·U и тропосферного n ≤ 0,05·U, где U - скорость передачи в канале; τ0 - длительность элементарного импульса. Учитывая, что в КВ-канале максимальная скорость передачи равна 300 бодам, легко определить максимальную длину блока, в котором параметр μi можно считать постоянным, она равна: n ≤ 60, или для тропосферного канала, где обычно U = 1200…2 000 000 бод -n ≤ 100 000.

Сделанное предложение будет справедливо для систем синхронизации с «зачетным отрезком» [2], при длине зачетного отрезка (ЗОТ), для КВ-каналов n ≤ 60 и для тропосферных каналов n ≤ 100 000 . Известно [2], что длина зачетного отрезка может быть равной: к+m ≤ n ≤ N=2^k-1 , где к - длина линейного рекуррентного регистра (ЛРР) датчика ПСП; m - емкость счетчика совпадений принятого из канала отрезка ПСП с опорной ПСП, формируемой на месте. Тогда для КВ-канала длина зачетного отрезка может изменяться в пределах: k+m ≤ n ≤ 60 , а для тропосферного канала: k+m ≤ n ≤ 100 000 . Для нахождения вероятности не-приема ПСП Р_н опишем модель канала синхронизации по «зачетному отрезку» при сделанных предположениях.

Разобьем ПСП на интервале анализа N’ на блоки из n элементов. Получим Z = N/n не пересекающих «зачетных от-

резков». Будем считать, что «зачетные отрезки» не зависимы между собой [2, 3] и на длине ЗОТ, по определению составного канала с переменными параметрами μ постоянно. Тогда для вероятности неприема ПСП будет справедливо равенство рнрз=и-РД<.                    (1)

где P_бо(n) -вероятность безошибочного приема блока из n символов в составном КПП.

Для вероятности правильного приема ПСП в составном КПП будет справедливо выражение:

Ррз= 1-ррз.

ПН              НX )

Известно [1], что вероятность безошибочного приема блока из n символов в составном канале находится как:

р» р^ И=еХ НУ • cq-i •s^ ’ где

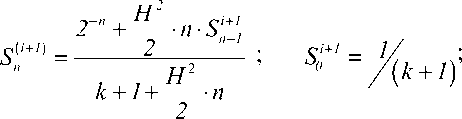
Q - число ветвей разнесения.

Подставляя (3) в (1) получим:

PT= 1-Q^k-iyc^.s^ .

■               1=0,

Вывод вероятности неприема ПСП в биномиальном, двоичном симметричном канале

По аналогии с составным каналом КПП для вероятности неприема ПСП в биномиальном, двоичном симметричном канале (ДСК) будет справедлива оценка:

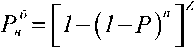
А для вероятности правильного приема можем записать:

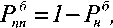
где P = 1/(2 + H²) ,

H² = a²/ σ ² - отношение средней энергии элемента сигнала на входе приемника к спектральной плотности помехи.

По найденным формулам (1), (4), (5), (6) произведем сравнительную оценку вероятности неприема ПСП Р_н в составном КПП при разнесенном приеме с автовыбором и в эквивалентном биноминальном канале ДСК.

JI ^^. ^-^^1

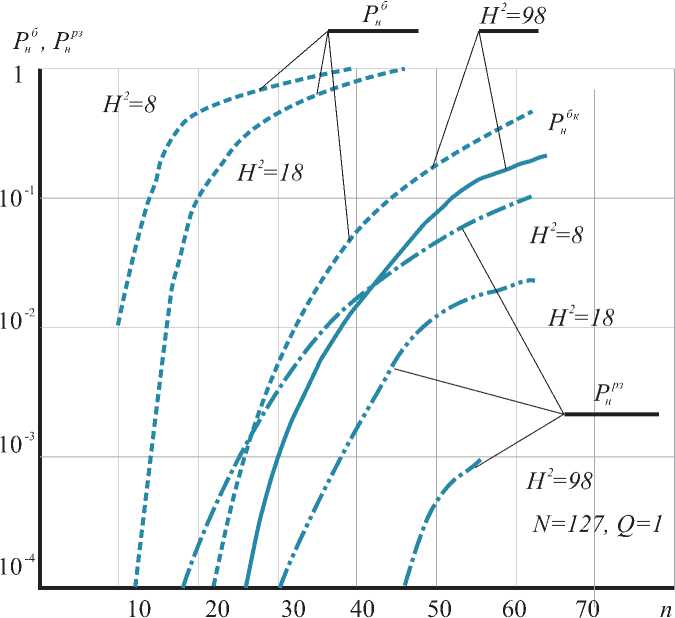
Рис. 1. Вероятность неприема ПСП в биномиальном и в составном квазибиномиальном каналах связи

Сравнительная оценка вероятности неприема ПСП в биномиальном и канале с релеевскими замираниями с автовыбором

По формулам (1), (4), (5), (6) для различных значений Q , n и N были произведены сравнительные расчеты на ПЭВМ. Результаты расчетов показаны на рис. 1 в виде графиков функций: р„ =^р:=ф^ и на рис. 2 в виде графиков функций: р^Ф^ур^ф^у

Анализ графиков рис. 1 показывает, что вероятность не-приема Рн в составном КПП гораздо меньше, чем в эквивалентном биноминальном канале. Причем при увеличении отношения сигнал\помеха Н2 эта разница увеличивается. Например, для N = 127, n = 20, Q = 1 и Н2 = 8, вероятность неприема в составном канале р на 3 десятичных порядка меньше, чем вероятность неприема в эквивалентном биномиальном канале р , а при Н2 = 18, эти вероятности различаются на 4 десятичных порядка. С увеличением же n эта разница убывает. Например, если для N = 127, Q = 1, H2 = 18 и n = 20 вероятность неприема в составном канале меньше вероятности неприема в биномиальном на 4 порядка, то при n = 50 эта разница убывает и составляет всего лишь два порядка. При увеличении длины ЗОТ n вероятность неприема в составном канале возрастает быстрее, чем в биномиальном, то есть синхронизация в составном канале более критична к выбору длины зачетного отрезка, чем в эквивалентном биноминальном канале. Однако при одинаковых вероятностях неприема вероятность ложной синхронизации в составном КПП будет меньше, чем в биноминальном, за счет удлинения самого зачетно- го отрезка. Действительно, из графиков видно, что при Ррз= рб= 10 в биноминальном канале n = 11, а в сос-н и тавном n = 40.

Следовательно, в составном канале быстрее можно войти в синхронизм. Это преимущество хорошо видно на рис. 2 . С увеличением длины зачетного отрезка n вероятность правильного приема в составном канале убывает значительно медленнее, чем вероятность правильного приема в эквивалентном биномиальном канале Р . То есть в составном КПП вероятность правильного приема ПСП сохраняется на достаточно высоком уровне даже при увеличении n в несколько раз. Расчеты показывают, что с увеличением ветвей разнесения Q или периода ПСП N качественные показатели системы синхронизации ПСП в составном КПП резко улучшаются. То есть вероятность неприема стремится к нулю, а вероятность правильного приема ПСП к единице ( Р^ → 0 , а Р → 1) ( рис. 3 ). Расчеты показывают, что прием с разнесением и автовыбором целесообразно использовать при Н²< 8 , так как на таких каналах эффективность одиночного приема резко падает, например, из рис. 2 видно, что при N = 127 , Q = 1 и Н² = 1 даже при n = 10 вероятность правильного приема ПСП рРЗ < 0,5.

Необходимо отметить, что при данной методике расчета не учитываются чистые интервалы длиной в n знаков, появляющиеся на стыках между смежными зачетными отрезками. Следовательно, (1) и (5) дают верхнюю оценку для Р_н . Для сравнения на рис. 1 показан график вероятности неприема ПСП, как функция от длины зачетного отрезка р = ϕ(n) , рассчитанный по точной формуле Козлова [4].

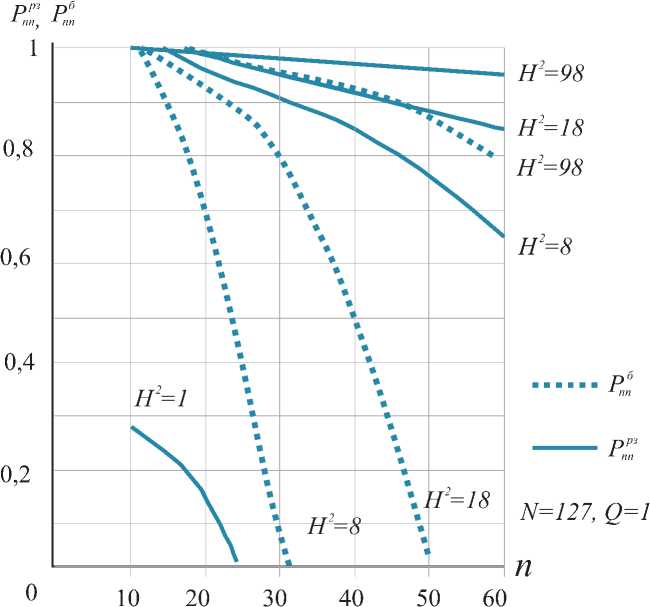
Рис. 2. Оценка вероятности правильного приема ПСП в биномиальном и в составном канале с замираниями

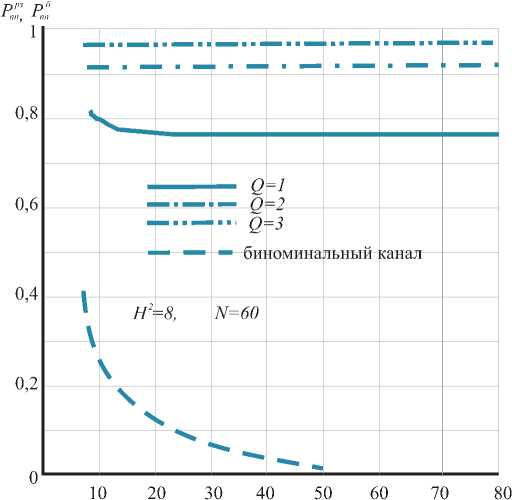
Рис. 3. Вероятность правильного приема ПСП в биномиальном канале и в канале с замираниями при ветвях разнесения Q = 1, Q = 2, Q = 3

Видно, что кривая н = ϕ(n) при одинаковых Н² идет ниже кривой вероятности неприема ПСП в эквивалентном биномиальном канале р = ϕ(n ), но вероятность неприема больше, чем в эквивалентном составном КПП р . То есть хорошо сохраняется общая закономерность изменения вероятности неприема в биномиальном канале, рассчитанные по формуле Козлова и по формуле (5), полученной в данной работе, что указывает на верность предыдущих выводов относительно сравнительного анализа синхронизации ПСП в составном и биноминальных каналах связи.

В отличие от биномиального канала, оценка (4) для составного канала будет мало отличаться от истинной. Действительно, в составном канале вероятность появления оши- бок на «g» фиксированных местах при одинаковых соотношениях сигнал/помеха Н2 больше, чем в биномиальном, и уменьшается при раздвижении единиц в образце ошибок [1], то есть можем записать:

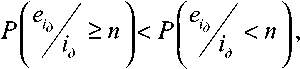
где

Р ^ п –

I /Zd )

вероятность появления образца ошибок e_Iд с расположением единиц на фиксированных местах, при условии, что расстояние между смежными единицами ≥ n ; i_д - расстояние между смежными единицами в образце ошибок e_Iд .

Из (7) видно, что вероятность появления чистого интервала из n символов между смежными ЗОТ будет меньше вероятности его непоявления, то есть существенного увеличения вероятности правильного приема ПСП в составном КПП р за счет неучтенных ЗОТ ожидать не приходится. В частности, расчеты показывают, что при n = 50 погрешность за счет неучтенных ЗОТ составит примерно два процента.

В заключение отметим, что полученные результаты можно обобщить на КПП с произвольными параметрами канала μ_i . Известно [1], что р не зависит от конфигурации ошибок в зачетном блоке, а определяется лишь появлением хотя бы одной ошибки.

На основании этого с достаточной уверенностью можно утверждать, что количественные результаты по синхронизации ПСП полученные для составных КПП, будут справедливы и для каналов с произвольным значением параметра канала μ_i .

При выводе формул (1), (4), (5) предполагалось независимость зачетных отрезков, хотя в реальных каналах связи такая зависимость может наблюдаться. Поэтому важно получение еще более общих соотношений для вероятностей Р_н , учитывающих зависимость смежных зачетных отрезков между собой. Этим вопросам посвящены дальнейшие исследования автора ■