Сравнительный анализ расчетов стакана подшипника методами сопротивления материала и программным комплексом Ansys

РАСЧЁТ СТАКАНА МЕТОДАМИ СОПРОТИВЛЕНИЯ МАТЕРИАЛА

Расчётная схема стакана представлена на рис.1. F A – осевая реакция в подшипнике.

Рисунок 1. Расчётная схема стакана

Установим опасные сечения и определим действующие в них напряжения.

Сечение а-а. Напряжённое состояние – срез.

F

τ = ^A , где S a-a – площадь сечения воспринимающего среза: S  = π D δ .

Поверхность 1. Напряженное состояние – смятие.

F т = A, где SA - площадь поверхности смятия - площадь контакта см1    SА торца подшипника и заплечника стакана:

_     ( D - 2 r )² d²

8, = п------ — - п —, где r

A ₄₄

–

радиус скругления наружного кольца

подшипника.

Сечение в – в. Напряжённое состояние растяжение.

^G P„ - .

в

F

^A , где S в-в

⁸ -

–

площадь сечения, воспринимающего растяжение:

S

D ² - DD

= п ¹-----

.

Сечение с – с. Напряжённое состояние – срез.

^{Т с} Р а - а

F

= -^A , где S_c-c - площадь, сечения, воспринимающего срез: 8 _с_= л ^ ^ .

Поверхность 2. Напряжённое состояние – смятие.

т см1

F A

S 2 ’

где S 2 – площадь поверхности смятия – площадь контакта фланца

стакана и корпуса редуктора.

_e    D. 2    ( D + 2 ^ )²

S ₂ = п -- - п ¹₄ 3  , где ^ - фаска в отверстии корпуса.

Условия прочности для каждого из сечений можно записать следующим образом:

n

т

^Т сР_а - a

n = ^ T - >  n 1                  см

Тсм, n в в

т т -

П с - с

^T T

^- с

n = О К a см

Здесь n – коэффициент запаса прочности; [n] – допускаемые значение коэффициентов запаса прочности для стакана на срез, смятие и растяжение, а [nCM ] - допускаемое значение коэффициента запаса прочности для материала корпуса; тт; а и Ок - пределы текучести для материала стакана и корпуса.

Наиболее опасным будет сечение, в котором отличие n и [n] будет наименьшим.

F_a = 8 кН; d=115 мм; D=125 мм; D, = 131 мм; D₂ = 141 мм; ^ = ^ ₂ = 3 мм;

^ = 2 мм; l=32 мм.

т = 150 Па; а = 200 МПа; а ^=80 МПа. Т               Т                  ТК

^Т СР„ - а

п - 125 - 3

= 6.79 МПа; т срс

п - 131 - 3

= 6.48 МПа;

О см

(125 - 2 - 2)² 4

- п -

= 7.19 МПа; a pв

131² - 125 2 п -

= 6.63 МПа;

° <М

141 2       (131 + 2 - 2) 2

--п--

= 6.15 МПа;

n

150              150              200

= 22.09; n „ =     = 23.15; n „ =     = 30.17;

6.79             с ^- с 6.48             в ^- в   6.63

ⁿ1 =

7.19

= 27.82; n =

6.15

= 13.01.

При наложении неупорядоченной сетки на стакан подшипника (рис.2), осевые напряжения на срезе а-а (рис.4) в ходе расчета в ANSYS оказались равными 7,27 МПа, а в месте перехода внешней боковой поверхности стакана в поверхность упорного торца (рис.4) 2,02 МПа.

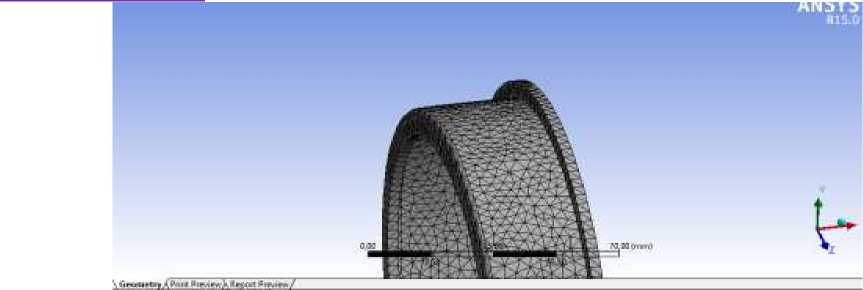
Рисунок 2. Неупорядоченная сетка

Рисунок 3. Осевые напряжения в стакане

Таким образом, осевые напряжения на срезе а-а, вычисленное методом сопротивления материалов оказалось в 1,071 раза меньше этого же напряжения, вычисленного с помощью пакета ANSYS.

При наложении упорядоченной сетки на стакан подшипника (рис.5), осевые напряжения на срезе а-а (рис.6) в ходе расчета в ANSYS оказались равными 6,77 МПа, а в месте перехода внешней боковой поверхности стакана в поверхность упорного торца (рис.7) 2,3258 МПа.

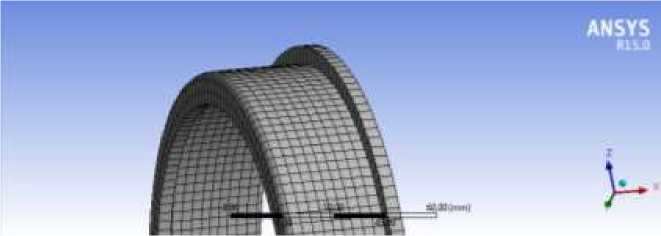
Рисунок 5. Упорядоченная сетка

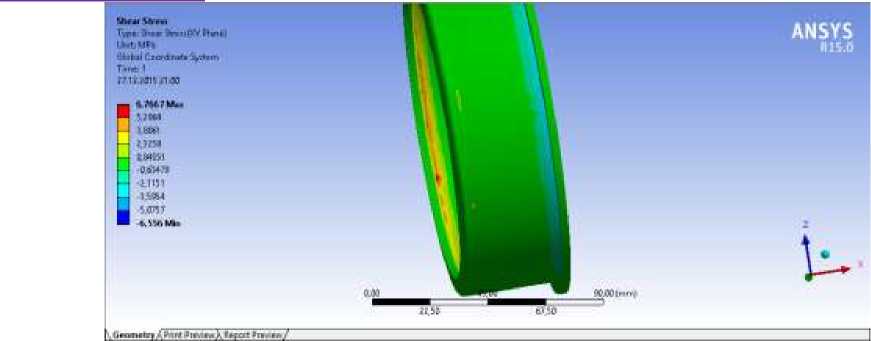
Рисунок 6. Осевые напряжения в стакане

Таким образом, осевые напряжения на срезе а-а, вычисленное методом сопротивления материалов оказалось в 1,003 раз больше этого же напряжения, вычисленного с помощью пакета ANSYS.

СРАВНЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ С РАССЧИТАННЫМИ ПО МЕТОДИКЕ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ

Сравнение полученных результатов произведём по сечению а-а (см. рис.1.).

Напряжение среза τ , рассчитанное по методичке сопротивления материалов равно 6,79 МПа. Максимальное рассчитанное напряжение с помощью программы ANSYS равное 7,27 МПа наблюдается в точке перехода внутренней цилиндрической части стакана в буртик, где имеется концентратор напряжения. Теоретическое значение наличии пустотелости коэффициент концентрации напряжения снижается, что учитывается дополнительным коэффициентов k=1,4…1,6 в зависимости от величины пустотелости. Таким образом, для нашей конструкции коэффициент концентрации принимается равным 1,4. Следовательно, если теоретическое значение напряжения умножить на коэффициент концентрации, то получим значение 9,5 МПа. В ходе расчета выяснилось, что при наложении упорядоченной сетки результат получается точнее, чем при использовании неупорядоченной сетки.