Сравнительный анализ расчетов тепловой эффективности оребрения при одномерной и двухмерной постановке задачи

Одним из способов интенсификации теплообмена между двумя средами, разделенными непроницаемой стенкой является оребрение той поверхности стенки, на стороне которой коэффициент теплоотдачи меньше. Расчет теплопередачи от оребренных поверхностей представляет собой сложную математическую задачу, поэтому на практике используют, как правило, упрощенные методики расчета тепловой эффективности оребрения. При этом обычно принимают следующие допущения [1,2]:

• а)    процесс стационарен;

• б)    теплопроводность материала ребра постоянна;

• в)    внутренние источники тепла отсутствуют;

• г)    температуры в основании ребра и окружающей среды постоянны;

• д)    толщина ребра мала по сравнению с высотой и соответственно градиент температуры в направлении, перпендикулярном боковой поверхности, пренебрежимо мал; для кольцевых ребер предполагается условие осевой симметрии, а прямое ребро имеет неограниченную длину в направлении, перпендикулярном плоскости чертежа (рис.1), т.е. температурное поле ребра одномерно;

• е)    теплоотдачей с торца можно пренебречь;

• ж)    коэффициент теплоотдачи по поверхности ребра постоянен.

Например, основное дифференциальное уравнение теплопроводности для ребра прямоугольного профиля при такой постановке имеет вид

^-^8 = 0

dy Х5₀

где: «9 = Т - Т_Ср - разность температур ребра и окружающей среды; а - коэффициент теплоотдачи наружной поверхности оребрения, Вт/(м²-°С); X - коэффициент теплопроводности материала ребра, Вт/(м-°С); у - координата, отсчитываемая от вершины ребра

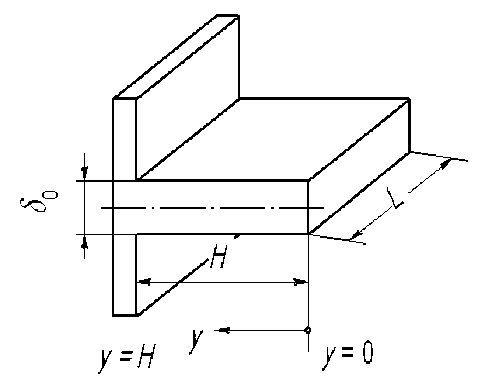
Рисунок 1. Продольные ребра прямоугольного и треугольного профиля

Общее решение этого обыкновенного дифференциального уравнения 2-го порядка с постоянными коэффициентами имеет вид

^ = С_хе'"^у+С₂е”'"^у                 (2)

где т = QodX 8of'\ м^-1; Зо - толщина основания ребра, м.

При граничных условиях 9'(//) = 3'0и

J3(0)

------= 0 решение уравнения (2) имеет вид dy                 '

Sochmv

------------'                        (э) chmH а тепловой поток, передаваемый ребром через единицу длины, равен q0 = X 50 m90 th mH,            (4)

где Н— высота ребра, м.

Эффективность ребра определяется как отношение теплового потока, действительно передаваемого ребром, к тепловому потоку, который передавало бы такое же идеально про водящее ребро (Л = да) с однородной температурой, равной температуре в основании ребра. Для продольного ребра прямоугольного про- филя эффективность определяется по формуле th /и/7

Л =----- mH

Аналогично можно получить соответствующие выражения и в случае продольного ребра треугольного профиля (см. рис.1).

Тепловой поток, передаваемый ребром единичной длины L = 1 определяется в этом случае по формуле

2а9₀/! (2т И)

ml, (2тН^

Эффективность ребра равна

_ 7, (2тЯ)

тШй ^2тН^ ’

где /о и /| — модифицированные функции Бесселя 0-го и 1 -го порядка соответственно.

Для радиального ребра прямоугольного профиля (рис.2) теплоотдача ребра равна q0 -2nr0b0Xm^0

(8) а эффективность вычисляется по формуле

₌   2r₀ I^nr^K^m^

т (г; - г; ) /₀ ( тг₀ )-К_х(тг,) + /, ( тг,) • К_о ( ту) (9) где го и г_е — внутренний и наружный радиусы ребра соответственно, м.

Для учета теплоотдачи с торца ребра часто используют метод Харпера-Брауна, при котором используют приведенные выше зави симости, в которых для учета теплоотдачи с торца используется фиктивная высота ребра.

Фиктивная высота ребра Нс принимается равной

Н_С = Н + ^-.               (10)

Большое число допущений, принятых при расчете тепловой эффективности ребер в одномерной постановке задачи, вызывает определенные сомнения в адекватности получаемых результатов. Для оценки правомочности использования приведенных выше зависимостей в работе с помощью некоммерческого пакета FreeFem++-cs 14.3 методом конечных элементов было исследовано влияние геометрических и физических параметров ребер плоской стенки и цилиндрической трубы на их тепловую эффективность.

В случае плоской поверхности были рассмотрены ребра прямоугольной и треугольной формы (рис. За, 36), для цилиндрической

поверхности рассматривались только прямоугольные ребра (рис.Зе).

При расчетах температура внутренней поверхности оребренной стенки принималась постоянной. На внешней поверхности ребра передача теплоты осуществлялась вследствие

теплоотдачи.

Ребра плоской поверхности принимались бесконечно длинными, что позволило решать задачу в двумерной постановке. Для сокращения времени на расчет, учитывая сим

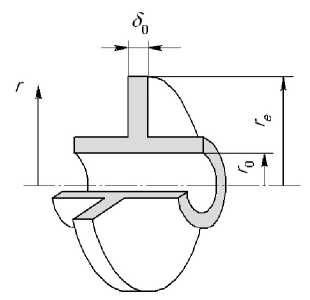
Рисунок 2. Радиальное ребро прямоугольного профиля

метрию, рассматривался только элемент, затушеванный на рис. 3.

В случае плоской оребренной поверх

ности решалась следующая задача

9^9 9^9

9²х Зу¹

(И)

со следующими граничными условиями

9(х,0) = Т№-Тс/,;

= «9 ,

5х ,v=s/2

где 3$/3п\г - производная по нормали к на

ружной поверхности ребра Г, °С/м.

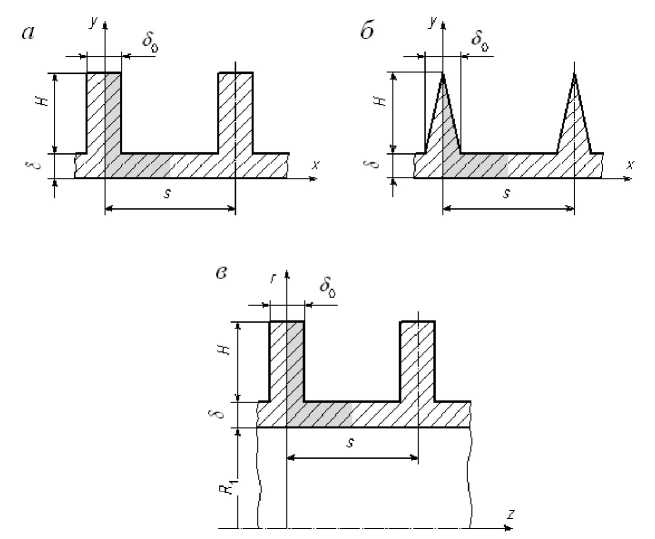
Рисунок 3. Схемы оребренных поверхностей

Для цилиндрической оребренной поверхности задача в цилиндрической системе координат при условии осевой симметрии формулируется следующим образом

529 1 59 529

—3—'----' г

5²г г dr 9z²

Начальные и граничные условия имеют вид q/d Л-т   т • 59  -о. 59    -о. 1 59 - а

Э (7?,,^) — Т_вн Т_сг, —0,         — О, X     — ссЭ,

8= _-=о 8z :=s/2             г где Л| — внутренний радиус цилиндрической поверхности, м.

Для оценки возможности пренебреже ния теплоотдачей с торца ребра были выполне ны расчеты при условии теплоизоляции торца ребра. В табл. 1 приведены результаты расчетов теплоотдачи продольного прямоугольного ребра, выполненные по формулам (4) и (5) и методом конечных элементов (МКЭ).

Расчет по формулам (4) и (5) проводился при следующих исходных данных: i9q =80 °C, а = 10 Вт/(м²-°С), Зо = 4 мм. При расчете методом конечных элементов дополнительно использовались значения s = 20 мм и 3 = 4 мм.

Как следует из приведенных в табл.1 данных формула (4) дает несколько большие значения теплоотдачи ребра, чем полученные МКЭ. Это объясняется тем, что при двумерной постановке задачи температура в основании ребра не является однородной. При этом отклонения увеличиваются с увеличением высоты ребра и уменьшаются с увеличением коэффициента теплопроводности материала ребра.

Аналогичные расчеты были выполнены и для продольного ребра треугольного профиля. Результаты приведены в табл.2.

Таблица 1 — Результаты расчетов тепловой эффективности продольного прямоугольного ребра

Н, мм	20		30		40		50
	ф-ла	МКЭ	ф-ла	МКЭ	ф-ла	МКЭ	ф-ла	МКЭ
4 = 50 Вт/(м-°С)
^о, Вт/м	31,58	31,42	46,61	46,28	60,79	60,23	73,94	73,12
п	0,987	—	0,971	—	0,950	—	0,924	—
4 = 200 Вт/(м-°С)
q0, Вт/м	31,89	31,85	47,64	47,56	63,16	63,01	78,37	78,14
п	0,997	—	0,993	—	0,987	—	0,980	—
4= 12800 Вт/(м-°С)
q0, Вт/м	32,0	32,00	47,99	47,99	63,99	63,98	79,97	79,97
п	1,0	—	1,0	—	1,0	—	1,0	—

Таблица 2 — Результаты расчетов тепловой эффективности продольного треугольного ребра

Н, мм	20		30		40		50
	ф-ла	МКЭ	ф-ла	МКЭ	ф-ла	МКЭ	ф-ла	МКЭ
4 = 50 Вт/(м-°С)
q0, Вт/м	31,38	31,44	45,96	45,86	59,67	59,12	71,42	71,01
'7	0,981	—	0,958	—	0,928	—	0,893	—
4 = 200 Вт/(м-°С)
qo. Вт/м	31,84	31,98	47,47	47,52	62,75	62,74	77,6	77,52
Л	0,995	—	0,989	—	0,981	—	0,970	—
4= 12800 Вт/(м-°С)
q0. Вт/м	32,0	32,16	47,99	48,10	63,98	64,06	79,96	80,02
и	1,0	—	1,0	—	1,0	—	1,0	—

Результаты расчетов, выполненных для радиального прямоугольного ребра, приведены в табл.З. Также можно отметить незначительные отличия в результатах, полученных по формуле (8) и методом конечных элементов.

При расчетах принимались значения го = 40 мм и 8 = 2 мм.

Для оценки правомочности использования метода Харпера-Брауна также были выполнены соответствующие расчеты. Результаты для продольного прямоугольного ребра приве- дены в табл.4.

Таблица 3 — Результаты расчетов тепловой эффективности радиального прямоугольного ребра

Н, мм	20		30		40		50
	ф-ла	МКЭ	ф-ла	МКЭ	ф-ла	МКЭ	ф-ла	МКЭ
4 = 50 Вт/(м °С)
о, Вт/м	9,89	9,85	15,96	15,86	22,44	22,26	29,08	28,77
п	0.984	—	0.962	—	0.930	—	0.890	—
4 = 200 Вт/(м °С)
q0, Вт/м	10,01	10,00	16,42	16,40	23,68	23,63	31,68	31,59
п	0.996	—	0.990	—	0.981	—	0.970	—
4= 12800 Вт/(м-°С)
q0, Вт/м	10,05	10,05	16,59	16,58	24,12	24,12	32,66	32,66
И	1,0	—	1,0	—	1,0	—	1,0	—

Таблица 4 — Результаты тепловой эффективности продольного прямоугольного ребра с учетом теплоотдачи с торца

Н, мм	20		30		40		50
	ф-ла	МКЭ	ф-ла	МКЭ	ф-ла	МКЭ	ф-ла	МКЭ
4 = 50 Вт/(м-°С)
q0, Вт/м	34,64	34,46	49,52	49,16	63,51	62,93	76,43	75,60
п	0,984	—	0,967	—	0,945	—	0,919	—
4 = 200 Вт/(м-°С)
q0, Вт/м	35,06	35,01	50,77	50,67	66,23	66,07	81,37	81,14
п	0,996	—	0,992	—	0,986	—	0,978	—
4= 12800 Вт/(м-°С)
q0, Вт/м	35,20	35,20	51,19	51,19	67,18	67,18	83,17	83,17
п	1,0	—	1,0	—	1,0	—	1,0	—

В табл. 5 приведены результаты расчетов МКЭ теплоотдачи с боковых стенок Q^ok и с торца Qtop продольных прямоугольных ребер различной высоты Н. Расчеты выполнены при следующих исходных данных: шаг 5=10 и 20 мм, толщина стенки 8=4 мм, толщина ребра 8о = 4 мм, коэффициент теплоотдачи а = 10 Вт/(м • С), коэффициент теплопроводности материала ребра Л = 50 Вт/(м-°С), температура внутренней поверхности стенки Т_Вн ⁼ Ю0 °C, температура окружающей среды Т_СР = 20°С.

Из приведенных данных следует, что теплоотдача с торца ребра составляет около 9 % от общей теплоотдачи для низких ребер и уменьшается до 3 % для высоких ребер.

Выводы

Результаты численных расчетов тепловой эффективности ребер различного профиля с использованием метода конечных элементов позволяют сделать вывод о том, что в исследованном диапазоне геометрических параметров ребер и теплофизических характеристик материала ребер результаты, полученные с использованием одномерных моделей теплопроводности ребер, незначительно отличаются от ре зультатов, полученных при двухмерной постановке задачи. В тоже время следует отметить, что использование метода конечных элементов позволяет не только значительно сократить временные затраты на проведение расчетов, но и рассматривать более сложные случаи постановки граничных условий.

Таблица 5 - Теплоотдача с торца и с боковых стенок продольного прямоугольного ребра

Н	20.0	30.0	40.0	50.0	60.00
Шаг ребер 5=10 мм
Qkok	31,35	46,12	59,99	72,78	84,39
Qtop	3,11	3,02	2,91	2,78	2,64
Шаг ребер s = 20 мм
Qbok	31,35	46,14	60,02	72,82	84,45
Qtop	3,11	3,02	2,91	2,78	2,64