Сравнительный анализ результатов построения ортогональных моделей при применении различных подходов к оценке корреляционно-спектральных характеристик в различных ортогональных базисах

годные аппроксимативные возможности по сравнению с ранее изученными системами базисных функций, а их применение в качестве базисных функций дает возможность повысить точность построения ортогональных моделей корреляционно-спектральных характеристик стационарных случайных процессов[1].

Ортогональные функции Бесселя дают наилучшие результаты при построении моделей КФ колебательного вида, постепенно затухающих на интервале существования. Это связано с тем, что уже первые взвешенные ортогональные функции Бесселя наиболее близко, по сравнению с другими базисными функциями, совпадают с формой анализируемых КФ этого класса, что обеспечивает допустимую погрешность аппроксимации при её минимальной глубине.

При построении ортогональных моделей корреляционно-спектральных характеристик выделяют несколько алгоритмов оценки коэффициентов разложения, основные из которых: апп-роксимативный[2], спектрально-аналитичес-кий[3], численно-аналитический подход[4]. Каждый из данных подходов имеет достоинства и недостатки.

Достоинствами построения ортогональных моделей с помощью аппроксимативного подхода являются [2]:

• 1)    сокращение объема хранимых данных;

• 2)    заданные алгоритмы и структура определения параметров модели;

• 3)    наглядность и компактность полученного аналитического выражения, легкость визуализации;

• 4)    возможность использования аналитического выражения для дальнейших аналитических исследований и преобразований с целью получения обобщенных вероятностных характеристик.

В качестве недостатка можно отметить невоз- можность построения ряда с требуемой точностью и произвольным числом членов ряда вследствие вычислительных погрешно-стей.

Достоинствами спектрально-аналитического метода являются[3]:

• 1)    снижение временных затрат при оценке коэффициентов разложения и построении ортогональных рядов;

• 2)    уменьшение объема вычислительных операций при оценке коэффициентов разложения и построении ортогональных рядов.

Недостатком является проведение операций с оценками, предполагающими наличие погрешностей, в том числе случайных, т.к. коэффициенты разложения не могут быть рассчитаны точно, особенно при построении моделей случайных функций (оценок корреляционных и спектральных характеристик).

Достоинствами аналитического подхода являются [4]:

• 1)    снижение временных и ресурсных затрат на получение конечного результата;

• 2)    повышение точности оценки корреляционноспектральных характеристик ортогональных рядов.

К недостатку можно отнести невозможность использования некоторых ортогональных базисов в качестве математического аппарата из-за отсутствия их аналитического представления.

Учитывая достоинства и недостатки данных методов, в данной работе рассмотрено развитие аппроксимативного подхода к построению ортогональных моделей путем добавления нового ортогонального базиса Бесселя в перечень функций, уже используемых в аппроксимативном анализе случайных процессов.

Учитывая описанные выше положения, проведем сравнение алгоритмов оценки коэффициентов разложения при применении численного подхода в базисах Лагерра, Лежандра, Дирихле; чис- ленно-аналитического подхода в базисах Лагер-ра, Якоби, численного подхода в базисе Бесселя.

В качестве примера рассмотрим задачу построения модели КФ идеального полосового шума:

sin(AtoT)     , .

f ( т ) =         e ■ cosk ^ . T ).        (1)

AtoT

e

Построим модель КФ (1) с применением выбранных подходов к оценке корреляционно-спектральных характеристик в различных ортогональных базисах для A ^ e = 0.5, OX = 5 со следующими данными: интервал дискретизации At = 0.09 , число ординат КФ N = 300 , число членов разложения ряда m = 150 .

В табл. 1 приведены значения параметра масштаба у и значения погрешности построения

/ то

j(f (t))2 ■ д(т,г)dt.

Из таблицы видно, что наилучший результат аппроксимации получен в ортогональном базисе Бесселя. Наиболее близкий результат получен в ортогональном базисе Лагерра с применением численно-аналитического подхода.

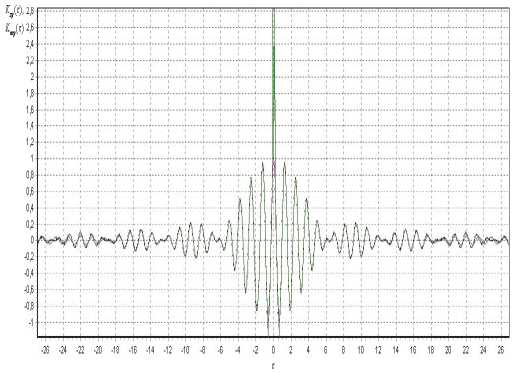
На рис. 1 представлена графическая интерпретация результатов построения модели КФ (1) в различных ортогональных базисах при применении различных методик построения.

Из рисунка видно, что на графике результатов аппроксимации в базисе Бесселя отсутствует “выброс” в нулевой точке, а также наблюдается более точное приближение исходной КФ на всем интервале её существования, что, в особенности, заметно на “хвостах”.

Далее рассмотрим задачу построения модели КФ вида:

f (t ) = e "^aT ■ cos ( ^ 0 ^ )         (2)

Таблица 1. Количественная оценка результатов построения модели КФ(3.34) с применением различных подходов к оценке корреляционно-спектральных характеристик в различных ортогональных базисах

Ортогональный базис и тип подхода	Значение параметра масштаба у	Погрешн ость аппроксимации 5
Бесселя, численный	0,029	0,04867
Лагерра, численны й	0,897	0,20476
Лежандра, численный	0,003	0,22425
Дирихле, численный	0,006	0,23729
Лагерра, численно-аналитический	4,444	0,06852
Лежандра, численно-аналитический	0,015	0,09338
Якоби (-0,5;0), численно-аналитический	0,015	0,09356
Якоби (0,5;0), численно-аналитический	0,015	0,09329
Якоби (1;0), численно-аналитический	0,029	0,09328
Якоби (2;0), численно-аналитический	0,015	0,09336
Сонина-Лагерра (1;1), численно-аналитический	4,444	0,2003
Сонина-Лагерра (2;1), численно-аналитический	4,444	0,3514

а)

б)

в)

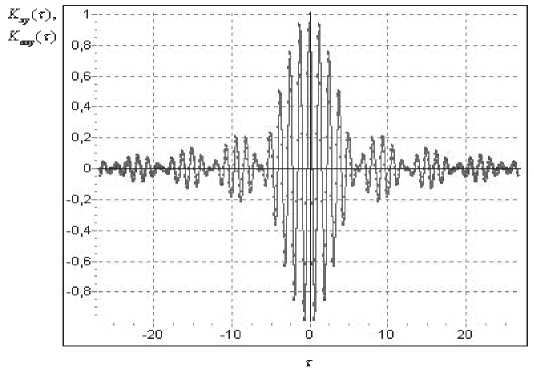
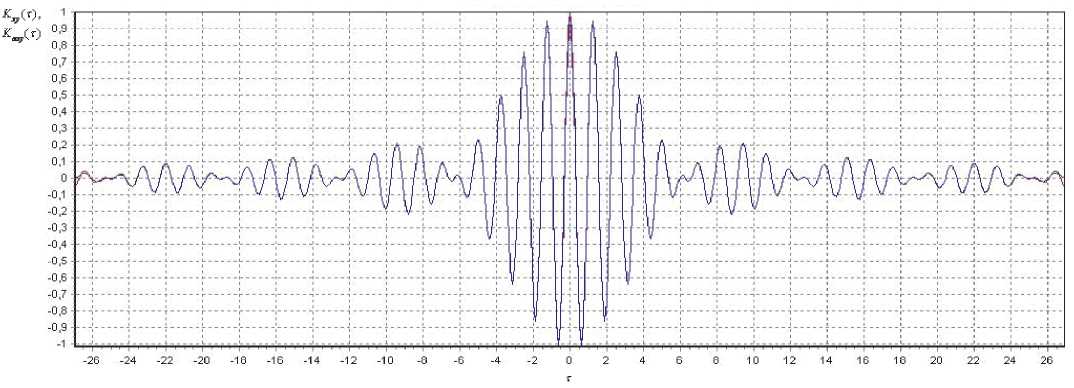
Рис. 1. Вид моделей КФ:

• а)    в ортогональном базисе Лагерра при применении численного подхода;

• б)    в ортогональном базисе Лагерра при применении численно-аналитического подхода;

• в)    в ортогональном базисе Бесселя при применении численного подхода

  с применением выбранных подходов при небольшой глубине аппроксимации для to ₀ /& = 5 со следующими данными: интервал дискретизации А г = 0,08165 , число ординат КФ N = 150 , число членов разложения ряда m = 71 .

Построение модели будем проводить с исполь- зованием алгоритмов оценки коэффициентов разложения при применении численного подхода в базисе Бесселя и численно-аналитического подхода в базисах Лагерра, которые показали лучшие результаты в предыдущем эксперименте.

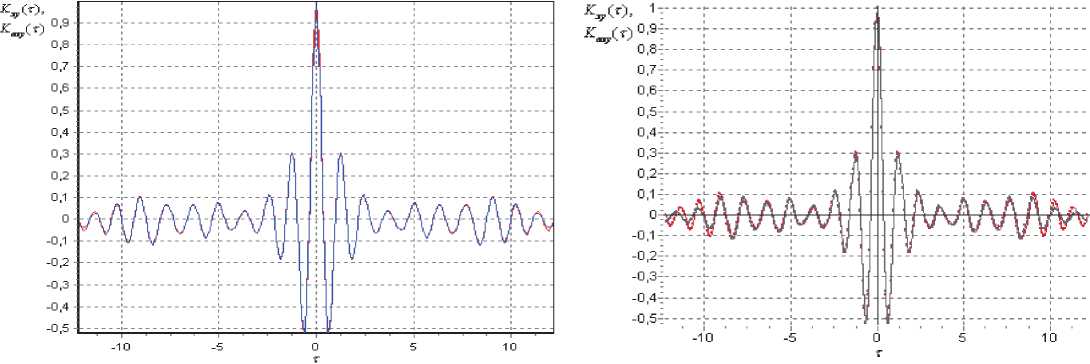
На рис. 2 представлена графическая интер-

а)                                                        б)

Рис. 2. Вид моделей КФ:

а) в ортогональном базисе Бесселя при применении численного подхода, погрешность аппроксимации б = 0,0762 ; б) в ортогональном базисе Лагерра при применении численно-аналитического подхода, погрешность аппроксимации б = 0,1115

а)

б)

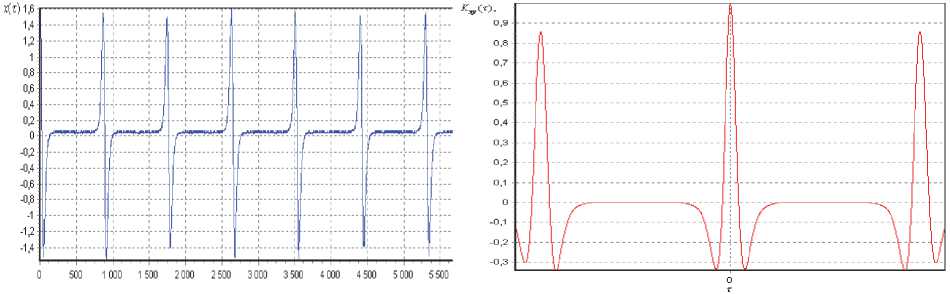
Рис. 3. Вид анализируемых характеристик: а) входной сигнал; б) КФ, соответствующая сигналу

• а)                                                       б)

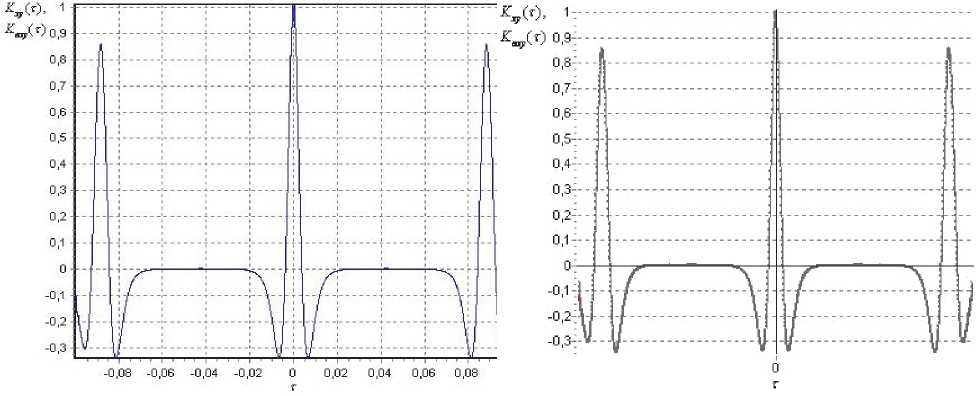
Рис. 4. Вид моделей КФ:

• а) в ортогональном базисе Бесселя при применении численного подхода, погрешность аппроксимации 5 = 0,0139; б) в ортогональном базисе Лагерра при применении численно-аналитического подхода, погрешность аппроксимации 5 = 0,0147

претация результатов построения модели КФ (2)в ортогональном базисе Бесселя с параметрами у = 0,0708 и m = 71 при применении численного алгоритма (погрешность аппроксимации 5 = 0,0762 ) и в ортогональном базисе Ла-герра с параметрами у = 4,899 и m = 71 при применении численно-аналитического алгоритма (погрешность аппроксимации 5 = 0,1115 ).

Лучший результат аппроксимации по параметру “относительная погрешность аппроксимации” получен в ортогональном базисе Бесселя.

Применение ортогональных функций Бесселя в качестве базисных при построении ортогональных моделей обеспечивает удовлетворение заданной точности аппроксимации не только для описанного выше класса КФ. Это связано с тем, что в формулу, задающую ортогональные функции Бесселя, входит параметр масштаба, изменение которого может заметно менять их свойства. Параметр масштаба в случае ортогональных функций Бессе- ля входит даже в выражение для весовой функции, что позволяет практически всегда согласовывать форму взвешенных ортогональных функций с формой поступающих на обработку КФ.

В качестве примера, подтверждающего сказанное, приведем результаты построения модели КФ сигнала, приведенного на рисунке 3 с числом ординат N=1000 и числом членов разложения ряда m=500 .

На рис. 4 приведены модели данной КФ в ортогональном базисе Бесселя с параметрами у = 7,9840 и m = 500 при применении численного алгоритма (погрешность аппроксимации 5 = 0,0139 ) и в ортогональном базисе Лагерра с параметрами у = 4000 и m = 500 при применении численно-аналитического алгоритма (погрешность аппроксимации 5 = 0,0147 ).

Лучший результат аппроксимации по параметру “относительная погрешность аппроксимации” получен в ортогональном базисе Бесселя.