Сравнительный анализ сил сопротивления движению грубодисперсных частиц вдоль радиальных лопастей турбомашин

Гродненский государственный университет имени Янки Купалы

Турбомашины с разгонным устройством центробежного типа, называемые также центробежными ускорителями, широко распространены в различных отраслях промышленности в качестве рабочих органов при создании сепараторов и классификаторов [1], систем пневмотранспорта [2, 3], воздуходувок [4], оборудования для подачи мелкодисперсного топлива в виде измельченного каменного угля [3, 4], центробежно-ударных измельчителей [5 – 7] и др. Несомненными достоинствами таких машин являются простота конструкции и технологичность в изготовлении, а также удобство обслуживания. Однако силовые и кинематические параметры работы турбомашин изучены недостаточно, что обусловлено сложностью протекающих в рабочей зоне фрикционных и аэродинамических явлений [3, 7]. Исследования силовых и кинематических параметров процессов транспортирования частиц в рабочих органах турбомашин не доведены до удобных на практике методик расчетов. Для тонкодисперсных пылевидных частиц принимается, что они движутся вместе с воздушным потоком со скоростью этого потока [4]. Для частиц более крупной дисперсности принимают некоторые упрощения и допущения. В частности, в работах [6, 7] не учитывается влияние аэродинамического сопротивления, а расчетные схемы составлены для численного моделирования с учетом трения частиц как по диску ротора, так и по его лопасти. В работе [8] методом верхней оценки учитывается аэродинамическое сопротивление без сравнения его с другими силами,

---------------------------\ due to the gravity of the particle can be neglected over most of the blade length. The influence of aerodynamic drag is more significant and should be taken into account in accurate technical calculations.

но не учитывается трение частиц о диск ротора. Анализ ограничен учетом центробежной силы, силы трения частицы о разгонную лопасть ротора в сочетании с аэродинамическим сопротивлением. Возможная оценка погрешности от таких приближений и допущений не произведена. Нет также сравнительной оценки соотношения сил трения от тяжести частиц и от действия сил Кориолиса.

Цель исследования – разработать методику и произвести с ее помощью сравнительный анализ сил сопротивления движению грубодисперсных частиц вдоль радиальных лопастей турбомашин. Постановка задачи и методика сравнительного анализа движущих сил и сил сопротивления

Математическое моделирование силовых параметров движения твердых частиц вдоль лопасти ротора произведем на примере широко распространенных в промышленности и исследовательской практике центробежного ускорителя с горизонтальным ротором-диском, снабженным радиальными лопастями. Схема ускорителя, а также действующих на частицу сил, приведены на рисунке 1.

На частицу массой m после соприкосновения с лопастью ротора действуют: сила тяжести G и уравновешивающая ее сила реакции диска; центробежная сила инерции F _è ; сила трения F _òð частицы о лопасть ротора или о диск ротора (зависит от положения частицы по высоте лопасти); сила аэродинамического сопротивления F _a ; сила инерции Кориолиса F _Ñ , прижимающая частицу к лопасти диска; реакция лопасти диска, равная по величине и действующая навстречу

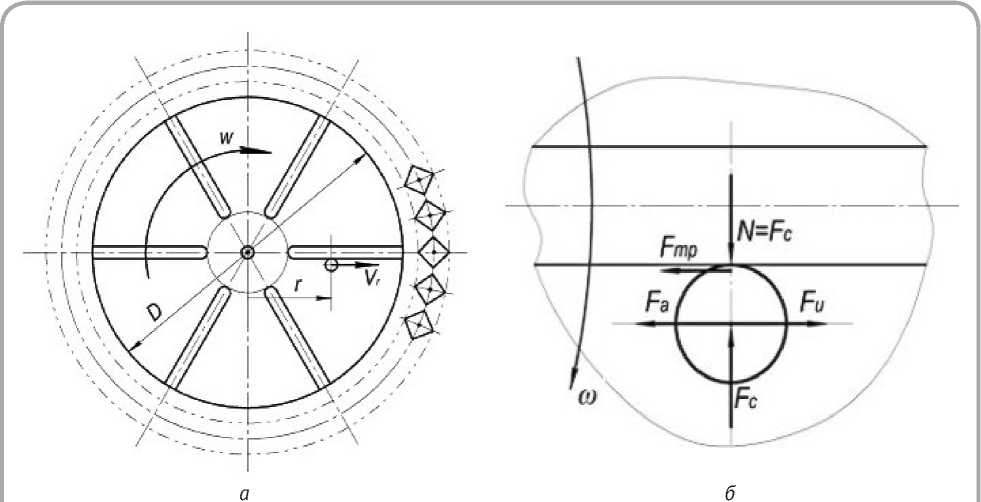
Рисунок 1 – К расчетной схеме для силового анализа работы центробежного ускорителя с горизонтальным ротором и радиальными лопастями: а – схема диска с лопастями (вид сверху); б – схема действующих на частицу сил

силе Кориолиса. При этом центробежная сила F_è направлена вдоль радиуса и вызывает ускоренное движение частицы, а сила трения F_òð частицы о лопасть ротора или о диск ротора и сила аэродинамического сопротивления F_a направлены навстречу движению. Выполним сравнительный анализ каждой из действующих сил.

Сила тяжести частицы G равна произведению ее массы m на ускорение от гравитации g , м/с ²

G = mg .            (1)

Сравним силу трения частицы о диск F_òðd , ( Í ) с центробежной силой инерции F_è . В соответствии с законом трения Амонтона-Кулона

Центробежная сила инерции F_è равна произведению массы частицы на ее центростремительное ускорение и направлена от центра вращения.

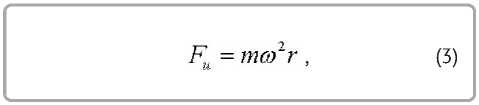
где ω – угловая скорость вращения ротора, ñ ^-1 ; r – расстояние от центра ротора до частицы, м .

Определим расстояние r , на котором сила трения частицы о диск не превысит некоторой малой величины λ (например, λ = 0,05) от центробежной силы. В математической записи с учетом (1), (2) и (3) это условие имеет вид

^d = /d^G = fd^S ,     (2)

f_dmg < Amro^r .         (4)

где f_d – коэффициент трения материала частицы о материал диска.

Сокращаем массу m в правой и левой частях уравнения и после преобразований получаем формулу для расчета соответствующего расстояния r

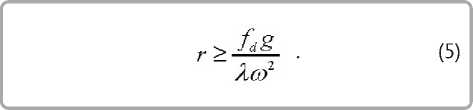
Как видно из (5), это расстояние не зависит от массы частицы, но зависит от угловой скорости вращения ротора и коэффициента трения материала частицы о ротор. Конкретные результаты расчета приведены во второй части статьи.

Кроме сил инерции и трения, на движение оказывает влияние сила аэродинамического сопротивления F _a , которую определяют, согласно [9], по формуле Ньютона

F_a = ^aApV² ,         (6)

где α – коэффициент лобового аэродинамического сопротивления, À – площадь сечения частицы по миделю ( м² ), под которой понимается площадь проекции частицы на плоскость, перпендикулярную вектору скорости набегающего потока, ρ – плотность воздуха, кг/м³ ; V – скорость движения частицы относительно воздуха, м/с .

При анализе будем учитывать, что воздух в роторных устройствах имеет окружную и радиальную составляющие полной скорости. Окружная скорость обусловлена переносным движением вместе с лопастью, а радиальная – уплотнением и относительным перемещением под действием центробежной силы в радиальном направлении. При точном решении в уравнении (6) надо использовать относительную скорость движения частицы, то есть разность радиальных скоростей частицы и воздуха. С целью упрощения анализа для мелкодисперсных пылевидных частиц принимают условие их движения со скоростью воздушного потока [4].

Для грубодисперсных частиц при оценочном анализе в первом приближении в качестве V примем радиальную скорость их движения.

Учтем также, что при движении шарообразных частиц в потоке газа экспериментально установлено существование трех характерных областей, каждой из которых соответствует определенный характер зависимости коэффициента лобового сопротивления α от числа Рейнольдса Re [9]: область ламинарного режима обтекания (Re ≤ 2)

область автомодельного режима ( Re ≥ 500), для которого α ≈ 0,44.

Подстановка значений коэффициента α из (7) и (8) в уравнение (6) показывает, что в ламинарной области сила аэродинамического сопротивления F _a пропорциональна скорости V в первой степени (подчиняется закону Стокса), во второй области – пропорциональна V^1,4 (не подчиняется закону Стокса и Ньютона), а в третьей – пропорциональна V² [9].

Проанализируем скоростные режимы движения частицы в воздушном потоке более подробно. При движении скорость частицы нарастает от нуля до некоторого рабочего значения. Из этого следует необходимость рассмотрения поэтапного движения частицы применительно к каждому из режимов – ламинарному, переходному, автомодельному. Учтем, что число Рейнольдса находят по следующей формуле [9]

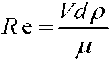
где μ – коэффициент динамической вязкости среды (для воздуха μ = 1,82 ∙ 10^-5 Па ∙ ñ [9]), d – диаметр частицы, м .

Из формулы (9) выразим скорость частицы относительно воздушного потока

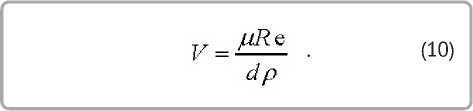
Уравнение (10) позволяет производить расчетную оценку диапазона скоростей относительного движения частицы и воздушного потока для ламинарного, переходного и автомодельного режимов. Результаты такой оценки, полученные с использованием уравнения (10), представлены в таблице 1. При выполнении оценочных расчетов принято значение плотности атмосферы ρ = 1,225 кг/м³ (Атмосфера стандартная. Параметры: ГОСТ 4401-81. (Действующий) (2004) – Введ. 01.07.1982. М.: ИПК Издательство стандартов, 2004).

Из таблицы видно, что ламинарный режим обтекания частиц воздушным потоком осуществляется при весьма малых значениях характеристических скоростей (29,7 мм/с для частиц диаметром 1 мм и 5,9 мм/с для частиц диаметром 5 мм). Поэтому данный режим не представляет практического интереса для промышленных и лабораторных турбомашин. Переходной режим может быть реализован на части длины лопасти, которая существенна для частиц малого диаметра (d < 1 мм). Причем с увеличением диаметра частиц длина этой зоны сокращается и, наоборот, при уменьшении диаметра – увеличивается. Грубодисперсные частицы (d > 1 мм) перемещаются преимущественно в автомодель- ном режиме.

Сила аэродинамического сопротивления зависит от скорости частицы, так же как и сила трения, обусловленная действием прижимающей частицу к лопасти диска силой Кориолиса ^F êîð ^{, Í}

^F^ = ^2m®^Vr ,        (11)

где V_r – скорость скольжения частицы относительно лопасти, м/с .

В связи с изложенным, найдем значения характеристических скоростей, при которых сила аэродинамического сопротивления не превысит некоторой малой величины λ (например, λ = 0,05) от силы трения частицы о лопасть диска. Для упрощения анализа будем рассматривать частицы сферической формы. В этом случае масса частицы m может быть вычислена как произведение плотности γ материала частицы ( кг/м³ ) на ее объем ( м³ )

m =----у .           (12)

Таблица 1 – Диапазон предельных значений скоростей, разделяющих области ламинарного, переходного и автомодельного режимов движения частицы
Диаметр частицы, мм	Оценочные диапазоны верхних границ скоростей ( м/с ) для типовых областей
	Область ламинарного режима	Область переходного режима	Область автомодельного режима
0,1	0,297	74,25	331,46
0,2	0,149	37,125	331,46
0,4	0,074	18,563	331,46
0,6	0,050	12,375	331,46
0,8	0,037	9,281	331,46
1,0	0,030	7,425	331,46
2,0	0,015	3,713	331,46
3,0	0,010	2,475	331,46
4,0	0,07	1,875	331,46
г      5,0	0,06	1,486	331,46 _______ 3

Примечание: верхняя граница автомодельного режима принята равной скорости звука в воздухе 331,46 м/с [10].

Условие обеспечения значения характеристических скоростей, при которых сила аэродинамического сопротивления не превысит некоторой малой величины λ (например, λ = 0,05) от силы трения частицы о лопасть диска, имеет следующую форму записи

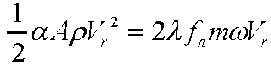
личины λ (например, λ = 0,05) от силы трения частицы о лопасть диска, имеет форму записи (14), но в рассматриваемом случае число Рейнольдса не зависит от скорости. Учитывая, что

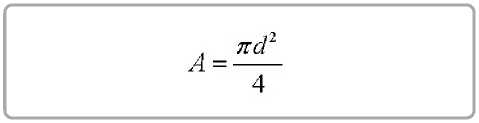
или

aApV_r = Mfpnco ,     (14)

и, подставив в (14) массу частицы из (11), получаем аналитическое выражение для определения значения скорости скольжения частицы вдоль лопасти ротора, при которой сила аэродинамического сопротивления в автомодельном режиме превысит заданную долю λ от силы трения частицы по лопасти диска, вызванной прижатием ее силой Кориолиса.

где f _ë – коэффициент трения частицы о лопасть ротора.

Переходной режим. Подставляем в (12) формулу (8) для определения коэффициента аэродинамического сопротивления α при переходном режиме и, с учетом (9) и (11), получаем после преобразований

6,9315^ = A f_Rdcoy .   (15)

Re ’

Формула (15) позволяет находить минимальное значение скорости скольжения частицы вдоль лопасти ротора, при которой сила аэродинамического сопротивления в переходном режиме обтекания частицы воздушным потоком превысит заданную долю λ от силы трения частицы по лопасти диска, вызванной прижатием ее силой Кориолиса.

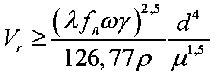
Автомодельный режим. Исходная формула для обеспечения значения характеристических скоростей, при которых сила аэродинамического сопротивления не превысит некоторой малой ве-

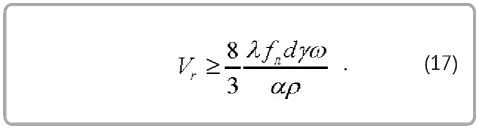
Полученные аналитические зависимости (16) и (17) позволяют производить сравнительный анализ силовых параметров движения твердых частиц вдоль радиальных лопастей турбомашин. Результаты сравнительного анализа силовых параметров и их обсуждение

Определим на первом этапе расчета расстояние r , на котором сила трения частицы о диск, обусловленная тяжестью частицы, не превысит 5 % от центробежной силы. Проведем количественную оценку этого расстояния r с использованием формулы (5) на примере перемещения кварцевого песка при угловой скорости ω = = 150 ñ^-1 . При анализе будем учитывать, что работа турбомашин обычно сопровождается в той или иной мере вибрацией, способствующей снижению коэффициента трения в сравнении с данными, полученными при статических испытаниях. Примем для оценочных расчетов, в соответствии с подходом, описанным в работах [7, 8], значение f _d = 0,3.

Расчеты показывают, что это расстояние составляет

Таким образом, на расстоянии свыше 2,6 мм от центра диска влияние силы трения частицы о поверхность диска, обусловленной тяжестью частицы, пренебрежимо мало для всех размеров частиц. Причем с увеличением угловой скорости ω вращения ротора это значение еще уменьшается, а с увеличением коэффициента трения несколько возрастает. В целом, данная величина остается пренебрежимо малой в сравнении с радиусами промышленных и даже лабораторных роторных машин и при технических расчетах ее можно не учитывать.

Для выполнения комплексного силового сравнительного анализа определим значения характеристических скоростей, при которых сила аэродинамического сопротивления не превысит 5 % от силы трения частицы о лопасть диска. Численную оценку произведем на примере частицы кварцевого песка диаметром 1 мм при значении коэффициента трения частицы о лопасть диска f _ë = 0,3 и угловой скорости вращения диска ω = 150 ñ^-1 . Расчеты с использованием аналитической зависимости (16) показывают, что это значение для переходного аэродинамического режима составляет

(0,05-0,3-150-2600)2,5 V > —---------— X г 126,77-1,225 1-Ю"12 x----------— = 217,096 м/с.

(1,82-Ю"5)'

Сравнение полученного значения скорости для данного диаметра частицы с предельным применительно к переходному аэродинамическому режиму из таблицы 1 ( V _r = 7,429 м/с ) показывает, что оно многократно (в 29,2 раза) выше предельного, то есть фактически не осуществимо на практике.

Вместе с тем с уменьшением размера частиц характеристические значения скорости, рассчитываемые по формуле (16), уменьшаются, а по формуле (10) – возрастают. В связи с изложенным, определим диапазон размеров частиц, для которых возможно перемещение вдоль лопасти ротора при переходном режиме аэродинамического сопротивления с соблюдением условия, что сила этого сопротивления не превышает наперед заданной доли λ от силы трения, обусловленной действием прижимающей силы Кориолиса. Приравняем верхние границы скоростей для этого режима из формул (10) и (16)

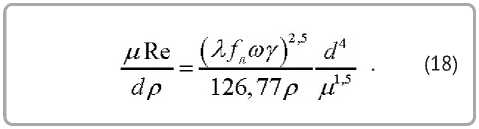
Верхним граничным значением числа Рейнольдса для переходного режима является Re = 500. С учетом изложенного, на основании (18), аналитическое выражение для расчета верхних граничных значений диаметра частиц принимает вид

■х

.

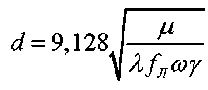
Подставив значения входящих в (19) величин ( А = 0,05; у = 1,82 ^ 10^-5 Па • с ; to = 150 с ^-1; Y = 2600 кг/м³ ), получаем d = 0,16140^-3 м = = 0,161 мм . При этом характеристическое значение скорости относительного движения частицы и воздуха, соответствующее верхнему пределу переходного режима, находим из формулы (10)

^• =

1,82-10 ” -500 0,16110э 1,225

= 46,14 м/с .

Аналогичный расчет для автомодельного аэродинамического режима при f _ë = 0,3; α = 0,44; γ = 2600 кг/м³ ; ρ = 1,225 кг/м³ ; ω = 150 ñ^-1 ; d = 1 мм после подстановки значений в формулу (16) дает

■\

_ 8 0,05-0,3-2б00-1-10~³-150

= 28,87 м/с .

0,44-1,225

Из этих результатов видно, что при скольжении частицы диаметром 1 мм со скоростью свыше 28,87 м/с сила аэродинамического сопротивления превышает 5 % от силы трения, обусловленной прижатием частицы к диску силой Кориолиса. Такие скорости характерны для значительной части длины лопасти (ее серединной и выходной зон). С увеличением диаметра частиц и угловой скорости вращения ротора соответствующее значение линейной скорости частицы возрастает, что указывает на уменьшение протяженности зоны. Из изложенного следует также, что только в начальной части лопасти влияние аэродинамического сопротивления на движение частицы можно считать малозаметным. В середине и на конце лопасти это влияние при точных технических расчетах целесообраз- но учитывать, особенно для частиц диаметром, заметно меньшим 1 мм.

Заключение

Результаты выполненных исследований позволили установить, что влияние трения частицы о диск ротора, обусловленное действием силы тяжести этой частицы, пренебрежимо мало и может не учитываться при проведении технических расчетов. При анализе аэродинамического сопротивления показано, что его влияние несущественно только в начальной части лопасти, а в середине и на конце лопасти это влияние целесообразно учитывать при точных технических расчетах для частиц диаметром, заметно меньшим 1 мм . Для таких частиц на большей части длины лопасти ротора ускоренное движение осуществляется под действием центробежной силы, ослабленной влиянием силы трения от прижатия частицы к лопасти под действием силы Кориолиса, а также аэродинамическим сопротивлением.