Сравнительный анализ способов передачи данных в широкополосных радионавигационных системах с частотно-манипулированными шумоподобными сигналами

Важным направлением расширения функциональных возможностей наземных широкополосных радионавигационных систем (РНС) является использование навигационного радиоканала для передачи данных о дифференциальных поправках, предназначенных для потребителей глобальных навигационных спутниковых систем ГЛОНАСС и GPS (в перспективе и системы GALILEO).2

Передача данных о дифференциальных поправках может осуществляться по отдельному радиоканалу, организованному с использованием известных способов уплотнения каналов (частотного, временного, кодового). Однако с целью сокращения энергетических и аппаратурных затрат в наземных РНС для передачи данных (дифференциальных поправок, служебной информации) и навигационной информации целесообразно использовать совмещенный радиоканал, применяя дополнительную цифровую модуляцию шумоподобного сигнала.

Выбор способа цифровой модуляции должен проводиться с учетом ряда факторов и, прежде всего, сохранения требуемых показателей качества РНС (точности, помехозащищенности и др.), обеспечения высокой точности и помехозащищенности канала передачи цифровой информации. При этом в широкополосных РНС могут использоваться как известные способы цифровой моду-

ляции, применяемые в узкополосных системах передачи информации (фазовая и относительная фазовая манипуляция, частотная манипуляция с непрерывной фазой), так и специфические виды модуляции (например, инверсная кодовая модуляция).3

В современных широкополосных РНС для формирования шумоподобных сигналов используется преимущественно фазовая манипуляция (ФМ) несущего колебания двоичной кодовой последовательностью (BPSK в англоязычной аббревиатуре). Примером служат спутниковые РНС ГЛОНАСС, GPS, GALILEO, а также наземные РНС SILEDIS, SPOT и др. [1]. Широкое использование ФМ при формировании ШПС объясняется, в первую очередь, стремлением максимально упростить формирование и обработку сигналов в широкополосных РНС. Однако с точки зрения спектральной эффективности более перспективным, чем традиционная ФМ, способом формирования ШПС является минимальная частотная манипуляция (МЧМ или MSK). В отличие от традиционных ШПС с фазовой манипуляцией, которым посвящено большое число работ [2–4 и др.], вопросам передачи, приема и обработки МЧМ-ШПС уделялось недостаточно внимания.

Цель данной статьи – сравнительный анализ помехоустойчивости способов дополнительной цифровой модуляции периодических шумоподобных сигналов с минимальной частотной манипуляцией.

Представление МЧМ-ШПС в отсутствие дополнительной цифровой модуляци и

Шумоподобные сигналы с МЧМ – это класс частотно-манипулированных ШПС с непрерывной фазой, которые можно представить в виде

5 (t) = Re{ S (t) exp (j2n f0t)} = ^2Pc cos [2n f0t + 0( t)] = = 72P [ I (t) cos (2n fо t)-Q (t) sin (2n fо t)],

S ( t ) = T2 P exp [ j 0 ( t ) ] = 72 P C [ I ( t ) + jQ ( t ) ] , j = V-T,

t

®(t )=2T1 d (t )dT

2T 0

где P _c – мощность сигнала; f ₀ – несущая (центральная) частота (начальная фаза равна нулю); S ( t ) – комплексная огибающая; Θ( t ) – функция, определяющая закон угловой модуляции (изменения во времени начального фазового угла несущей); I ( t ) = cosΘ( t ) и Q ( t ) = sinΘ( t ) – действительная и

N - 1

мнимая компоненты нормированной комплексной огибающей; d (t) = ^ dkrect (t - kT) -двоичный k=0

модулирующий сигнал, соответствующий кодовой псевдослучайной последовательности (ПСП) d 0 , d 1 , ^, d_N -1 с элементами d_k e { - 1, + 1 } ; rect( t ) - прямоугольный импульс единичной амплитуды и длительности T (индекс частотной манипуляции m_f = ∆ f T = 0. 5, ∆ f = f ₁ – f ₂, f ₁ = f ₀ + 1/4 T и f 2 = f 0 - 1/4 T - значения частоты для dk = +1 и d_k = -1 ( k = 0, N - 1) соответственно); N - длина кодовой ПСП, определяющая длительность ШПС T _c = NT [5].

В отличие от ФМ-ШПС, комплексная огибающая которого является действительной функцией времени, комплексная огибающая (1) содержит действительную и мнимую компоненты, представляющие собой видеочастотные ШПС со сдвигом на T (элементы ШПС Q(t) запаздывают на T относительно элементов ШПС I(t) с тем же порядковым номером). Такое представление позволяет считать МЧМ разновидностью квадратурной ФМ «со сдвигом» (OQPSK), широко используемой в цифровых телекоммуникационных системах для передачи данных.

Отличительной особенностью квадратурных ШПС I ( t ) и Q ( t ) в случае МЧМ служит то, что их элементы представляют собой импульсы косинусоидальной формы и длительности 2 T , повторяющиеся с полутактовой частотой 1/2 T и манипулированные по «фазе» кодами { c_k } и { s_k }:

” го

I ⁽ t ) - 2 c - I о ⁽ . - 2 ^-T > , Q ( t > = 2 s - I о ( t - < ^{2 -} + 1 > ^T>

Iо (t )=

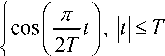
0, t >  T ,

где I ₀( t ) – одиночный импульс, определяющий форму элемента ШПС.

Элементы кодов { c_k } и { s_k } также принадлежат двоичному алфавиту {–1,+1} и связаны с элементами исходной кодовой ПСП, определяющей закон частотной манипуляции, соотношениями [6]

d 2 - = c - s - ,   d 2 - + i =— c - s - - 1 , ^- = ..., — 1, 0, 1, - .

При записи (2), (3) полагалось, что коды { d_k }, { c_k } и { s_k } – периодические последовательности, образованные повторением кодов заданной длины. В случае, когда { d_k } – М -последовательность длины N , коды { c_k } и { s_k } имеют длину L = 2 N . Причем коды { c_k } и { s_k } имеют структуру чередующихся сегментов ± c и ± s , образованных на одном периоде кода { d_k } : { c_k } = …, c , – s , – c , s , c , … и { s_k } = …, s , c, – s , – c , s , …. Это следствие неидеальной «уравновешенности» М -последовательности (число 1 и –1 соответственно равно ( N +1)/2 и ( N –1)/2), в силу чего фаза 0( t ) претерпевает изменения на п/2 на интервале, равном периоду повторения T = NT . ^п

Поскольку квадратурные сигналы являются «гармоническими» функциями кусочно-линейной фазы Θ( t ) : I ( t ) = cosΘ( t ) и Q ( t ) = sinΘ( t ), то при периодическом повторении кода { d } фаза Θ ( t ) определяется как                                                                        п

^(t ) = ^(* — T ) + if 1

а квадратурные периодические сигналы (с периодом повторения 4 T _п)

I_п ( t ) = ..., I ( t ) , - Q ( t ) , - 1 ( t ) , Q ( t ) , I ( t ) , ...,

Qn (t ) ..., Q(t ), I (t ), Q(t ), I (t ), Q(t ), ..., где I(t) и Q(t) соответствуют i = 0.

Следуя принятой терминологии [6], образованный таким образом сигнал будем называть периодическим МЧМ-ШПС в отличие от финитного сигнала (1) с числом элементов, равным N, и длительностью Tс = NT. Используя такое определение периодического ШПС и оставляя, как часто принято, термин «сигнал» для описания комплексной огибающей, модель периодического МЧМ-ШПС представим в виде го

го

го                                 го

5(t) = S5(t) = ^Xexp 1j 0(t- iT)+i2

го

i =-го

Cos I ®(t - iT ) + i- I + j sin I ®(t - iT ) + i- I , V                2 / V                2 /

где 5 i ( t ) - финитный сигнал (1) на интервале t е [ iT , ( i + 1 ) T_n ] .

Представление МЧМ-ШПС при дополнительной цифровой модуляции

Применительно к периодическому МЧМ-ШПС (4) при дополнительной цифровой модуляции для комплексной огибающей можем записать

«

i=-м      ^ L                                      JJ где Θм(t) – составляющая фазы, обусловленная цифровой модуляцией данными и определяемая при ФМ и ЧМ, соответственно,

П

®м (t- T )=const(t И Di- 1) 2

и

м(t-iTn)=mfDin(t-iTn)+mfn£Dk, te[iTn,(i+1)T,]; Tn                        k < i где D e{-1,+1} - информационный символ длительностью T = T; m, - индекс частотной i                                                                                              D пf манипуляции.

Дополнительная фазовая манипуляция . Учитывая представление МЧМ-ШПС (1), а так

’ рЦ/,»

exp ⁽_А ⁽ t ^{- i}T n ) ) . D, t _{eK( i +} 1 ) T n ] , перепишем (5) в виде

,_______ Го [ n-11

• *5 (t ) = 72Pf Zp,Z[CkI0 (t - k 2T - iTn) + jskI0 (t-(2 k +1) T - iTn W

i =-m t k = 0

где n = ( N + 1) /2 – число элементов кодовых последовательностей { c_k } и { s_k } на периоде повторения ШПС. 4

Как следует из (6), дополнительная ФМ шумоподобного сигнала с МЧМ может быть осуществлена путем инверсной модуляции кодовых последовательностей { c_k } и { s_k }, определяющих законы модуляции квадратурных ШПС. При передаче символа D_i = +1 используются прямые (основные) коды { c_k } и { s_k }, а при передаче символа D_i = –1 – инверсные коды, в которых все элементы заменяются на противоположные. При этом код { d_k }, определяющий закон широкополосной ЧМ, а следовательно, и вид модулирующей функции Θ( t ) сохраняются неизменными вне зависимости от того, какой символ (+1 или –1) передается (при смене символа изменяется лишь начальная фаза Θ_м, принимая значения 0 или π).

В общем случае период повторения кодов { c_k } и { s_k } равен 4 T _п, а не T _п. Однако фиксированный сдвиг π/2 начальной фазы комплексной огибающей на каждом периоде T _л может быть устранен путем привязки фазы ©( t ) = 0 в моменты t = iT , i = …–1,0,1,… . В этом случае коды { c } и { s } имеют период повторения T .

п                   kk              п

Дополнительная частотная манипуляция . При использовании для передачи данных дополнительной ЧМ с непрерывной фазой начальная фаза МЧМ-ШПС претерпевает на каждом интервале [ IT п , ( i +1) T п ] сдвиг на ± mfn (знак приращения фазы определяется знаком информационного символа). В случае m = 0.5 имеем узкополосную МЧМ с законом изменения фазы ^f

9 м ( t - T ) = D.n ( t - И. ) + П у D k . t ₆ [ ,r , . ( i + 1 ) T n ] . 1 = .... - 1.0.1.... 2 T            ² k < i

Дополнительная инверсная кодовая модуляция. Способ инверсной кодовой модуляции широко используется в широкополосных РНС с традиционной ФМ: символы D_i = +1 передаются кодом { d_k }, а противоположные символы D_i = –1 – инверсным кодом {– d_k }. Таким образом, модифицированная периодическая кодовая последовательность { D_id_k } состоит из случайным образом чередующихся сегментов длины N основной и инверсной кодовых последовательностей.

В случае широкополосной кодовой МЧМ функция Θ( t ), определяющая закон угловой модуляции ШПС, также инвертируется, если передаваемый символ D_i = –1:

^е м ⁽ t ^ D i ^е < t -T n     2

t e[ iT , , ( i + 1 ) T n ] , i = _- 1,0,1....

Поскольку квадратурные ШПС при данном способе цифровой модуляции определяются как

= cos I 0( t - iT ) + iП I, l п^ 2)

= D, sin 0(t - iT ) + i— , i ( ( п) 2 J’

I (t) = cos0 (t) = cos D I 0(t - iT ) + in i IV п7      2

ем (t )=sin ем (t )=sin Diett - IT,)+in убеждаемся, что такой способ передачи данных сводится к инверсной модуляции только кода {sfc} (мнимая компонента в (6)), в то время как код {cfc} остается неизменным независимо от передаваемого символа. В этом заключается принципиальное отличие МЧМ-ШПС от шумоподобных сигналов с ФМ, для которых указанный способ передачи данных эквивалентен передаче противоположных сигналов и позволяет реализовать потенциальную помехоустойчивость. В случае же МЧМ инверсная кодовая модуляция соответствует передаче ортогональных сигналов (синфазные составляющие совпадают, а квадратурные составляющие - противоположные).

Выражение (6) для комплексной огибающей периодического МЧМ-ШПС в этом случае преобразуется к виду

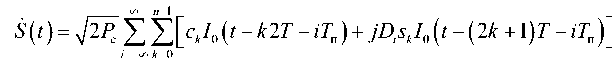
to    n - 1

i =-to k = 0

Анализ помехоустойчивости способов дополнительной цифровой модуляции

Сравним помехоустойчивость рассмотренных способов цифровой модуляции МЧМ-ШПС, полагая, что прием сигналов осуществляется на фоне аддитивного гауссовского белого шума при идеальной фазовой и кодовой синхронизации (оптимальное различение двух детерминиро- ванных с игналов равной энергии). Вероятность ошибочного приема в этом случае определяется известной формулой [7]

Р ош = 1 4 q     1 ,                          (8)

2 J где Ф(x) – интеграл вероятности; q – отношение «сигнал/шум» в полосе информационного символа (равное 2E/N0 независимо от вида цифровой модуляции ШПС); r – модуль коэффициента

" различаем^ых си гнало,, определяемо,окак *

r = R2 (0)--j м t) 5 .( t) dt,

R ₁₂(t) - иормированная взаимнокорреляционная функция (ВКФ) комплексных огибающих

5 1 ( t ) и 5 ₂( t ) шумоподобно го сигнала, соответствующих информационным символам D 1 = +1 и

Т      2

D 2 = -1; 2 E = j | 5 ( t )| dt = 2 Р_сТ — э^нергия комплексной огибающй сигнала (4) за период Т _п ( E - 0

энергия действитель н ого сигнала з ( t ) ( 1 )).

Дополнительная фазовая манипуляция. Используя выражение (6), для коэффициента корреляции при ^ФМ получаем очевидный результат:

TD

r- = — j exp (j 0( t)) exp [-j (©( t) - n )] dt = -1, . E 0

поскольку сигналы S1(t) и S2(t) противоположны, а для вероятности ошибки (8) имеем рош =1 -Ф( q), что совпадает с известным результатом [7].

Дополнительная частотная манипуляция. В случае узкополосной МЧМ ( m_f = 0.5) коэффициент корреляции

T D

Р TD      ( (

r = Ec Jexp I jl®( t)

V

V

П 11                               П II,

+---- 1 exp - j 0( t)--1 dt =

D )) I I       D1!) J)

= -I

D 0

n cos t

I Td

П

+ j Sin —t T

dt .

Действительная составляющая в (9) определяет синфазную компоненту нормированной ВКФ (интеграл от первого слагаемого во втором равенстве), которая равна нулю, а мнимая составляющая – квадратурную компоненту (интеграл от второго слагаемого равен j 2 / π). Поскольку при когерентном приеме используется только синфазный канал демодулятора, то в соответствии с (9) имеем r = 0.

Таким образом, передача цифровой информации посредством дополнительной узкополосной МЧМ шумоподобного сигнала (с широкополосной кодовой МЧМ) соответствует различению ортогональных сигналов, применительно к которым вероятность ошибочного приема [7]5 ,

Рош = 1 -ф( q/^), т.е. имеет место проигрыш 3дБ в помехоустойчивости по сравнению с ФМ.

Однако, как и в случае широкополосной кодовой МЧМ, можно использовать двойственную природу данного вида модуляции (частотной манипуляции с непрерывной фазой или квадратурной ФМ «со сдвигом»), чтобы повысить помехоустойчивость передачи данных. Для этого необходимо использовать относительное кодирование (на передаче) и декодирование (на приеме) в соответствии с алгоритмом

D2, = CiSi, D2i+1 =-CiSi-1, i =..., -1,0,1,..., и, кроме того, осуществить когерентный прием каждого из двух квадратурных ФМ-сигналов, выделив последовательности информационных символов {Ci} и {Si} соответственно. Очевидно данный способ передачи данных есть не что иное, как способ относительной ФМ, широко ,                                          ’rm используемой в узкополосных системах, для которой вероятность ошибочного приема [7]

Р ош = 1 -ф ² ( q ) ,

• т. е. по сравнению с традиционным способом передачи и приема ЧМ-сигналов (как ортогональных сигналов) имеет место выигрыш в помехоустойчивости (при q . 1).

Использование межсимвольной фазовой связи, присущей ЧМ-сигналам с непрерывной фазой, позволяет повысить помехоустойчивость приема. Достигается это применением алгоритма приема «в целом» следующих подряд m информационных символов (время анализа mT_D ) с принятием решения о значении первого символа (с задержкой на mT_D ). Этим, в частности, можно объяснить и тот факт, что помехоустойчивость алгоритма приема МЧМ-сигнала как сигнала с квадратурной ФМ «со сдвигом» выше, чем помехоустойчивость оптимального приема ортогональных сигналов. Действительно, указанный алгоритм – частный случай алгоритма приема «в целом» при времени анализа 2 T_D ( m = 2).

При m ≥ 3 использование межсимвольной фазовой связи при МЧМ обеспечивает выигрыш в помехоустойчивости по сравнению со способом ФМ. Однако с увеличением m резко возрастают аппаратурные затраты (число каналов демодулятора равно 2 ^m ), в то время как увеличение помехоустойчивости замедляется. Практически целесообразным представляется значение m = 3 (выигрыш по сравнению с оптимальным приемом противоположных сигналов составляет около 0.5 дБ [7]). Столь парадоксальный на первый взгляд результат объясняется следующим. В теории оптимального приема время анализа полагается равным длительности информационного символа, а при использовании межсимвольной связи оно в m раз больше, что приводит к увеличению в m раз отношения «сигнал/шум» в каждом канале демодулятора. Хотя число различаемых сигналов при приеме «в целом» составляет 2 ^m (против двух в случае ФМ), вероятность ошибочного приема каждого символа в этом случае может быть меньше, чем при оптимальном приеме ФМ-сигналов, когда время анализа T_D .

Следует заметить, что несмотря на всю привлекательность данного способа передачи данных как наиболее помехоустойчивого способа практическая его реализация весьма проблематична. Связано это, прежде всего, с трудностями осуществления когерентного приема МЧМ-ШПС с дополнительной цифровой МЧМ. В отличие от широкополосной кодовой МЧМ, при которой фазовый сдвиг на +π/2 за период Tп носит регулярный характер и может быть учтен при формировании опорных сигналов, при узкополосной МЧМ из-за случайности передаваемых символов это осуществить технически сложно (учет случайного фазового сдвига на ±π/2 за длительность символа).

Дополнительная инверсная кодовая модуляция. В этом случае коэффициент корреляции различаемых сигналов определяется как

₁ T_{D                                                 1} T_D

Г = ™ J exp(jD®*))exp(-jD2®(1))d / J/os(20(1)) + jsin(20(1))]d?" 2E0                                TD 0

Учитывая только действительную компоненту нормированной ВКФ (соответствует когерентному приему при идеальной синхронизации), для модуля коэффициента корреляции имеем r = 0, т. е. данный способ модуляции эквивалентен передаче ортогональных сигналов (МЧМ-ШПС). При этом помехоустойчивость приема та же, что и в случае применения для передачи данных узкополосной МЧМ (при традиционном способе приема ортогональных сигналов). Различие двух способов цифровой модуляции заключается в том, что если при МЧМ центральная частота принимает значение f ₀ + D_i / 4 T_D при передаче символа D_i = ±1, то при инверсной модуляции она равна f ₀ независимо от того, какой символ передается. В техническом аспекте способ инверсной кодовой модуляции предпочтительнее, чем способ узкополосной МЧМ, так как отпадает необходимость учета фазового сдвига D_i π / 2 несущей при формировании когерентного опорного сигнала в демодуляторе (при приеме ( i +1)-го символа).

Заключение

Проведенный сравнительный анализ способов дополнительной цифровой модуляции ШПС показывает, что наиболее предпочтительным для применения в широкополосных РНС с шумоподобными МЧМ-сигналами является способ ФМ как обеспечивающий потенциальную помехоустойчивость. Данный способ может быть реализован как путем непосредственной фазовой манипуляции МЧМ-ШПС, так и косвенно (путем фазовой манипуляции квадратурных видеоча-стотных компонентов). При этом отпадает необходимость в применении относительного кодирования цифровой информации, поскольку из-за специфики широкополосных РНС неоднозначность фазовых измерений отсутствует (устраняется с использованием результатов измерений задержки кода).

Способ инверсной кодовой модуляции проигрывает в помехоустойчивости способу дополнительной ФМ около 3дБ при равных аппаратурных затратах.

Применение дополнительной узкополосной МЧМ для передачи данных теоретически позволяет повысить помехоустойчивость приема за счет использования межсимвольной фазовой связи. Однако сопряжено это с решением ряда технически сложных проблем (в первую очередь, проблем с реализацией когерентного приема). Потери в помехоустойчивости из-за отказа от этого способа передачи этого в пользу способа ФМ невелики (менее 1дБ) и могут быть скомпенсированы применением других системотехнических решений (например, помехоустойчивого кодирования).