Сравнительный анализ типов вейвлет-преобразований в задаче сжатия спутниковых изображений

Задача сжатия сигналов основывается на некоторых преобразованиях, целью которых является переход от исходного сигнала к системе обобщенных координат, их селекции по определенному критерию приводящему к сокращению числа исходных данных и восстановлению сигнала с помощью обратных преобразований.

Одной из идей компрессии изображений является сжатие с помощью дискретных ортогональных преобразования, определенных на развертках двумерных областей [1].

Предлагается использовать для сжатия изображений квазинепрерывные развертки сигналов [2], вейвлет-преобразование квазинепрерывных развертоксигналов и использованиедляселекции вейвлет-коэффициентов свойства мультимасш-табного самоподобия, связанного с фрактальной структурой спутниковых изображений.

Методы оценки и определения показателя фрактального самоподобия

Для статистического анализа выбран фрагмент изображения размером 1024×1024 пикселей спутника Landsat 5 (см. рис. 1).

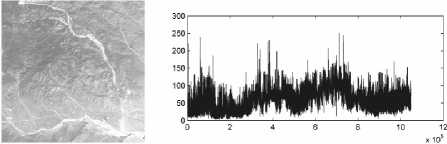
Рис. 1. Тестовое изображение со спутника Landsat 5 и его квазинепрерывная развертка

Квазинепрерывные развертки типа Пеано-Гильберта использовались для преобразования двумерной матрицы изображения в одномерный ряд. Важной задачей, которую необходимо было решить, было определение показателя фрактального самоподобия Херста.

Анализ нормированного размаха

Основываясь на исследовании различных явлений (например, изменения уровня воды в реке), Херст разработал нормированную безразмерную меру, способную описать изменчивость [3]. Эту меру он назвал нормированным размахом (R/S). Для заданного набора наблюдений               с выборочным средним вводится понятие размаха

R(n) = maxN _f — min A.,             (1)

i<« ³   \3

где к              ___ _____ то есть разность между максимальным и минимальным отклонением.

Эта характеристика отличается от размаха временной последовательности случайной величины , который равен временной ряд самоподобным и, если является, получить грубую оценку Н.

Этот результат может быть использован, чтобы оценить показатель Херста по заданному ряду наблюдений. Однако если наблюдения берутся из кратковременно зависимого процесса, тогда показано, что

M

Rfn)

Sfn)_

cn⁰⁵ при n —> CO,

где d – конечная положительная константа, не зависящая от n . Этот случай может рассматриваться как характеристика процесса, не обладающего свойством самоподобности.

R(n) = maxZv - min^^ \3   \3

Вместо него выбрана величина, учитывающая накопление и характеризующая изменчивость величины относительно среднего значения. Для описания изменчивости более удобна нормированная безразмерная характеристика:

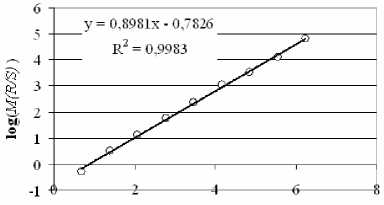
log(n )

Рис. 2. График R/S-статистики для развертки спутникового изображения: у = 0,898 х - 0,783 - линия рег

Rfn) S(n)

max/V - mint^ \3   ]3

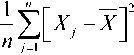
max( О, A,, A,,..., A_H) - min( 0, A,, A,,..., A_|?) S(n)

Херст назвал это отношение нормированным размахом и показал, что для многих природных явлений справедливо эмпирическое соотношение

рессии (y = l_Og М

Л 1^1

л^- = log w); R² - величина дос

товерности аппроксимации (квадрат коэффициента смешанной корреляции)

M

Rfn)

S(n),

~ сп^н при n —> co,

где с – положительная конечная константа, не зависящая от n . Прологарифмировав обе части (5), получим

График изменения дисперсии

Для самоподобного процесса, связь между дисперсией объединенного процесса и размером блока m формулируется следующим образом:

ст²1X*"'* I « ат ¹⁵, при т -^ со,

log< M

Rfn) S(n)

»//log(/?) + log(c)

при n —> CO.

Таким образом, параметр Н можно оценить, изобразив график (см. рис. 2)

где а – некоторая конечная положительная константа. Прологарифмировав обе части (8), получим зависимость

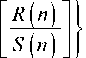
от

log (cr (А^'"* j j = —Рlogf' т) + logf а ), при т —> со.

, и, используя полученные точки, подоб-

рать по методу наименьших квадратов прямую линию с наклоном Н .

R/S-метод не слишком точен, поскольку дает оценку только уровня самоподобности во временном ряде. Поэтому данный метод может использоваться только для проверки, является ли

Следовательно, можно получить оценку , вычислив для различных значений m и отображая результаты графически от log ( m ),

провести через полученные точки прямую линию по методу наименьших квадратов. Оценку для определим как отрицательный наклон прямой линии, подобранной по методу наименьших квадра-

тов. Поскольку известно, что Н связан с р через ^н = ^х"' это дает оценку для Н , равную .

Результат использования этого метода для измеренной трассы показан на рис. 3, где была выбрана логарифмическая шкала значений m и log( m ) отображалось на фоне log ^g² ^Л^^"¹ jj. Отметим, что дляlog( m )> 2 значения log (а² (^'"'^ выглядели случайно. Это происходит потому, что число блоков размера m пропорционально размеру выборки, а чтобы дать точную оценку дисперсии блоков, для которых log( m ) > 2, полученное число точек недостаточно. Поэтому эти точки исключались при использовании метода наименьших квадратов. Формула прямой, полученной этим методом (рис. 3), имеет вид у = -0,4131 х - 2,0421, определяя оценку, и, соответственно, оценку Н= 0,793.

■2

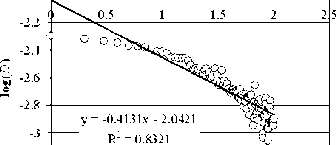
-J 2

log(m)

Рис. 3. График изменения дисперсии для развертки спутникового изображения: y = –0,413 x – 2,042 – линия регрессии (у = logger² (jf’"'¹)), х = log(«)); R² – величина достоверности аппроксимации (квадрат коэффициента смешанной корреляции)

Как и в случае R/S-анализа, метод изменения дисперсии – лишь эвристический метод. Оба метода используются в дальнейшем при различных ограничениях; например, они могут быть действительно обоснованны при малом количестве статистических данных, доступных наблюдению из отдельной выборки самоподобного процесса. Следовательно, изменение дисперсии может использоваться только для того, чтобы проверить, является ли временной ряд самоподобным, и если является, то получить грубую оценку Н .

Анализ мультимасштабной структурной функции

Показатель самоподобия разверток спутниковых изображений определялся на основе логарифмических асимптотик мультимасштабных структурных функций [4], определяемых в дискретном случае соотношением s^T^+k)-^ •    (10)

Z = 1

где M = 2 ^2m , m x m – размер изображения, f™ – пиксели изображения масштаба m . Логарифмические асимптотики структурной функции иллюстрирует рис. 4.

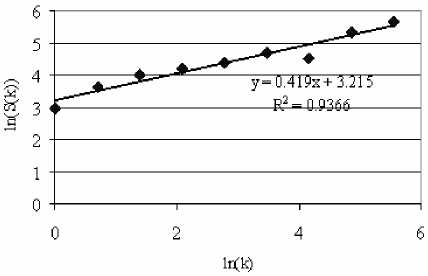
Рис. 4. Логарифмические асимптотики мультимасш-табной структурной функции: y = 0,419 x + 3,215 – линия регрессии y = ln( S ( k ), x = k ; R² – величина достоверности аппроксимации (квадрат коэффициента смешанной корреляции)

Линейный характер асимптотики позволяет по углу наклона определить показатель фрактального самоподобия Херста H.

Определение оптимальных порогов фильтрации коэффициентов разложения и выбор типа вейвлет-преобразования развертки изображения

В качестве параметров, по которым будут сравниваться типы вейвлетов, выбираются число нулевых коэффициентов ^zr (основной показатель, отвечающий за коэффициент сжатия изображения), коэффициент корреляции исходного и восстановленного после сжатия сигнала C , доля энергии исходного сигнала, которую сохраняет восстановленный сигнал ^eoccm ’ максимальная абсолютная разность сигналов ^ max (максимум шума восстановления), а также среднеквадратическое значение шума восстановления °er . Под шумом восстановления понимаем далее разность между исходным и восстановленным сигналом.

В качестве сравниваемых выступают вейвлеты Хаара (haar), Добеши (db10), Мейера (dmey), симплеты (sym), койфлеты (coif). Прямое и обратное вейвлет-преобразование производится при помощи расширения Wavelet Toolbox пакета программ Mathworks MATLAB.

Выбор оптимального порога фильтрации вейвлет-коэффициентов

На рис. 5. изображен исходный сигнал (s), а также его аппроксимирующие (низкочастот- ные – a12) и детализирующие (высокочастотные ) уровни разложения. Эти уровни в сумме и дают исходный сигнал. Сущность фильтрации, заключается в том, что все коэффициенты разложения, значения которых ниже определенного уровня, считаются нулевыми и в дальнейшем сжатии (или передаче по каналу связи) занимают минимальное число бит. Следует, однако, выбрать такие пороговые уровни, чтобы при достаточном коэффициенте сжатия сохранилась основная информация изображения, в том числе редкие, аномальные сигналы.

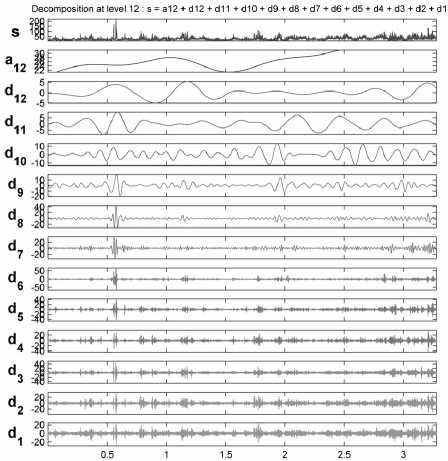
Рис. 5. Вейвлет-разложение развертки спутникового изображения по системе функций Добеши

Традиционным методом выбора пороговых значений,является равенство сохраненной энергии сигнала (выраженной в % ) и числа нулевых вейвлет-коэффициентов. Однако данный метод учитывает только одну характеристику качества сигнала – его энергетику. Однако даже при высоких значениях порога отсечки сохраняется до 90% энергии сигнала.

Для выбора оптимальных порогов отсечки воспользуемся свойством масштабной инвариантности вейвлет-коэффициентов. Покажем, что они удовлетворяют свойству масштабного самоподобия.

Пусть – случайная функция, описывающая развертку изображения (случайный фон). Предположим, что – фрактальная функция и, следовательно, допускает представление в форме интеграла по траекториям винеровского случайного процесса :

^(0= j(?-^zT ^dw^

(И)

Представим в виде вейвлетовского разложения

(12) j к где       – какая-либо система ортогональных вейвлетов.

Докажем следующее утверждение: коэффициенты вейвлет-разложения фрактальной функции являются масштабно-инвариантными случайными величинами.

Действительно, коэффициенты вейвлетовско-го разложения определяются соотношением где

Здесь – вейвлет-функция. Из (11) и (12) следует

—co 0

Произведем в интеграле (13) замену переменных                 и, учитывая масштабные свойства винеровского гауссовского процесса, 1

выражающееся соотношением можно получить представление

Из соотношения (14) следует свойство масштабного самоподобия вейвлет-коэффициентов

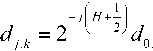
Равенство (15) следует понимать в статистическом смысле,а именно,любые статистические моменты случайной величины на масштабном уровне j масштабно-самоподоб-ны (самоаффинны) и выражаются через соответствующие моменты на некотором исходном масштабном уровне j = 0. В частности, для дисперсий, из соотношения (15) следует равенство

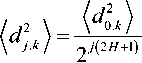
где V/ – знак усреднения по статистическому ансамблю.

Данные вычислительных экспериментов, проведенных с гильбертовскими развертками спутниковых изображений, показывают, что дисперсия вейвлет-коэффициентов удовлетворяет масштабному соотношению (16). На рис. 6 в логарифмической шкале отображена зависимость дисперсии вейвлет-коэффициен-тов различных уровней разложения от номера уровня (нулевому уровню выражения (16) соответствует уровень с максимальным номером и число коэффициентов, большим 30 (для эффективного расчета дисперсии), в противном случае имеем бедную статистику) для разных типов вейвлетов. Регрессионная линия проведена только для массива данных haar . Как видно из графика на рис. 6, условие (16) выполняется для всех типов вейвлетов.

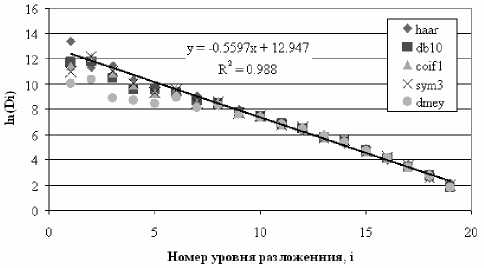
Рис. 6. Дисперсии масштабных уровней вейвлет-ко-эффициентов: y = –0,5597 x + 12,947 – линия регрессии ( y = ln ( D _i ), x = i ); R² – величина достоверности аппроксимации (квадрат коэффициента смешанной корреляции)

Поэтому пороговые значения фильтрации вейвлет-коэффициентов устанавливаем на уровне СКО на данном уровне. Чтобы сократить объем вычислений в условиях использования цифровых сигнальных процессоров на борту спутника дистанционного зондирования, основные статистические данные (показатель самоподобия H , дисперсия) следует вычислять по уровням с меньшим числом коэффициентов (близким к нулевому уровню).

Выводы

Таким образом, используя данные принципы, проведем разложение, фильтрацию и обратное преобразование развертки тестового спутникового изображения.

Таблица 1. Сравнительные характеристики различных типов вейвлетов

	Н	С		Е .% вэост
Вейвлеты Хаара	0.5485	0.9656	0.7787	99.3881	34	7.2435
Вейвлеты Добеши	0.5144	0.9096	0,9326	98.6303	55	11.5761
Койфлеты	0.5284	0.8803	0.9537	98.3063	68	13.2193
Симплеты	0.5234	0,8697	0,9538	97.9017	63	13.7552
Вейвлеты Мейера	0.4399	0.9729	0.8981	99.6118	31	6.4462

Данные вычислительных экспериментов показывают, что наилучшее качество восстановленного изображения показывают вейвлеты Хаара и Мейера, так как они имеют минимальное значение ^emm- ^{И G}er . Однако коэффициент сжатия спутникового изображения для данных типов меньше,чем для вейвлетов Добеши, симплетов и койфлетов, которые обеспечивают меньшую точность декомпрессии. В зависимости от требований к качеству космических изображений (высокая четкость снимкаилисохранениеаномальныхобъектов), для сжатия выбирается определенный тип базисных функций.При этом следует учитывать сложность реализации того или иного типа вейвлет-разложения на цифровых сигнальных процессорах (DSP). Наибольшей простотой реализации отличается вейвлет Хаара, так как вычисление низкочастотных и высокочастотных коэффициентов сводится в этом случае, к нахождению полусумм и полуразностей соседних отсчетов исходного сигнала.