Сравнительный анализ точности нелинейных моделей при прогнозировании состояния системы на основе марковской цепи

Пусть некоторая система S может находиться в одном из состояний конечного (или счетного) множества возможных состояний S ₁ , S ₂ ,…, S_n , а переход из одного состояния в другое возможен только в определенные дискретные моменты времени t ₁ , t ₂,…, t_n , называемые шагами. Предположим, что вероятность перехода из любого состояния S_i в любое состояние S_j не зависит от того, как и когда система S попала в это состояние. В таком случае функционирование системы S описывается дискретной цепью Маркова.

В качестве x ₁ , x ₂,…, x_m будем рассматривать внешние факторы, предположительно оказывающие влияние на систему S . В зависимости от области исследования данные переменные могут нести в себе различную смысловую информацию.

Требуется на основе имеющихся данных системы, включая воздействие внешних факторов, построить прогноз состояний системы на следующем шаге ( k+ 1) с помощью нелинейных моделей , а также сравнить точность прогнозирования.

Традиционно, задачи такого плана решаются с помощью нахождения матрицы переходных вероятностей P . Переходной вероятностью p_ij называют условную вероятность того, что из состояния i (в котором система оказалась в результате некоторого испытания, безразлично какого номера) в итоге следующего испытания система перейдет в состояние j . Таким образом, в обозначении p_ij первый индекс указывает номер предшествующего, а второй – номер последующего состояния.

Введем начальное распределение вероятностей марковской цепи:

В частном случае, если первоначальное состояние системы S в точности известно S (0) = S_i , то начальная вероятность P_j (0) = 1, а все остальные равны нулю. Поскольку система может пребывать в одном из n состояний, то для каждого момента времени t необходимо задать n ² вероятностей перехода p_ij , которое удобно представить в виде следующей матрицы:

II РЛ =

^f p 11

( P n 1

p 1 n

\

.

p nn

Так как в каждой строке матрицы помещены вероятности событий (перехода из одного и того же состояния i в любое возможное состояние j ), которые образуют полную группу, то сумма вероятностей этих событий равна единице. Другими словами, сумма переходных вероятностей каждой строки матрицы перехода равна единице:

n

E p_y = ¹             (3)

i , j

Такая матрица называется матрицей переходных вероятностей. Если матрица перехода на шаге ( k + 1) будет известна, то прогноз распределения вероятностей состояний системы может быть получен, используя распределение вероятностей состояний системы за предыдущий шаг. То есть, распределение вероятностей состояний на следующем шаге вычисляется как:

P ( k + 1) = л ( k ) P ( k,k + 1),        (4)

где р(k) – безусловное распределение вероятностей состояний системы.

Для нахождения переходных вероятностей будем использовать нелинейные модели из класса логистической регрессии [1].

Рассмотрим модель бинарной логистической регрессии, записываемую уравнением:

p ( ^i,j ) =

1 + e ^- ax ’

где p ( i,j ) – переходная вероятность, ax - линейная комбинация предикторов:

___ m + 1

ax = «^ j ⁺ S^a j ' x¹ ' ,         (6)

1 = 2

где a - неизвестные параметры модели, m - количество внешних факторов.

Перепишем модель следующим образом:

m + 1

exp( a 1 + S a il • x¹ ' ) p (i , j ) =                                . (7)

1 + exp(a\ + S a j • x^{1 1})

1 = 2

Получили формулу для нахождения переходной вероятности, с учетом воздействия на систему внешних факторов. Однако при этом не учитываются прошлые переходы системы, которые также могут оказывать некоторое влияние. В связи с этим, добавим в уравнение дополнительный фактор, показывающий, был ли совершен рассматриваемый переход шаг назад.

Тогда с учетом данной поправки модель примет следующий вид:

m + 1

^{exp( a} j ⁺ S ^a j • ^{x + a} ij y j - 1 )

P (i , J ) =------------4+---------------------- • (8)

• ^{1    + ex}p^{( a} j ⁺ S ^a • ^{x - 1 +} a ⁺² y j .J

1 = 2

В общем случае введем историю предыдущих переходов:

Hj = {y„, k = 1,..., j -1}.(9)

Следовательно, общая модель для нахождения переходной вероятности будет выглядеть так:

m+1

^exp^{( a} ij ⁺ S ^{a 1} ■ ^{x - 1 +} S A r ■ У ч-r )

P ( i , j ) =-------------------------^, (10)

• 1    + exp(a* + S aj ■ x1 -1 + S Air • Уч-r) l =2

где q – порядок модели, показывающий учет количества предыдущих переходов, A — неизвестные параметры.

На следующем шаге необходимо оценить все неизвестные параметры. Существует несколько способов, наиболее распространенными из которых являются метод наименьших квадратов и принцип максимального правдоподобия. Применим последний из них для модели общего вида.

Согласно принципу максимального правдоподобия за оценки параметров принимаются те значения, которые дают максимум для функции правдоподобия:

v

F ( f ) = П P (‘, J ) ’i t¹ - P <‘, J rf" У (11) i = 1

где 7 7 = ( a ¹,..., a m ^{+ 1} , A V--, A q ) - неизвестные параметры, v – объем выборки, g_i - зависимая переменная, принимающая следующие значения:

Г 1, если был совершен переход для заданной пары состояний ( i ^ j ) ’ =

^ 0, иначе.

Запишем логарифм функции правдоподобия и найдем максимум:

v

F ⁽ у ) = S g i ^ln p ⁽ i , ^j ) ^{+ (1 -} g i ^{)ln(1 -} p ⁽ i , ^j )) ^.(12) i = 1

F( у ) ^ max

В результате получим систему нелинейных уравнений относительно неизвестных параметров :

wo(y) = S p(i, j)- S1=0, {i: ’i =1} w1(n) = S p(i, j)x 1 - Sx 1 =0, {i: ’i =1}

^ w m ⁽ П ) = S p ⁽ i , j ) ^x m - S ^x m = ⁰,      (13)

{i: ’,=1} wm +1(У ) = S p(i , j)УУ-\ - S Уу-1 = 0,

{i: ’i=1} wm+q (n) = S p(i, j)yj-q - S Уу-q = 0 {i: ’i =1}

Существует множество способов решения систем нелинейных уравнений, но одним из обеспечивающих наилучшую сходимость является метод Ньютона-Рафсона [2], в котором поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации.

Возьмем следующее начальное приближение для параметров модели:

у⁰ = (0,...,0).

В качестве итерации запишем:

— k+1 —k      —k    i —k у = у - W(у ) J 1(у ), (15)

где

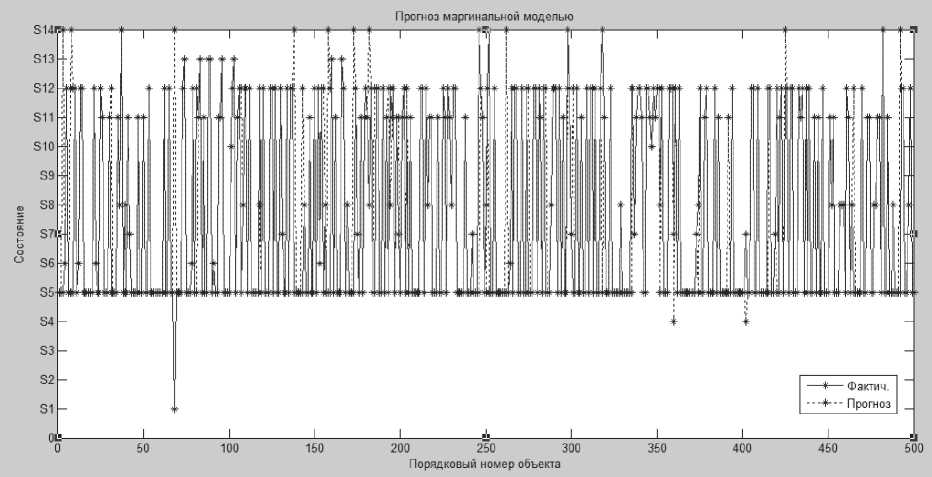
Рис. 1. Прогноз на базе маргинальной модели

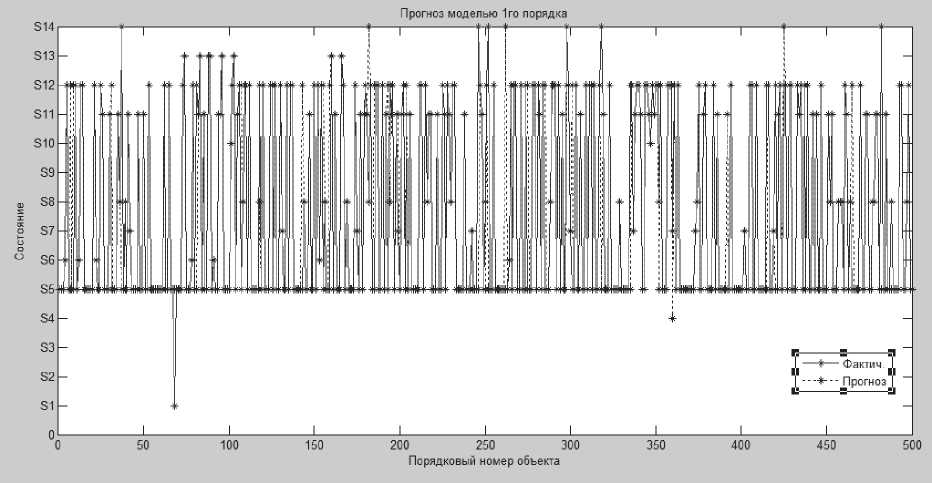
Рис. 2. Прогноз на базе модели 1-го порядка

W(Л ) = ( w₀(^ k ), W t (^ k ),-

• -, w m (^ X w m _{+ 1}⁽П X-.., w m ₊ q ⁽Л )),

• - вектор частных производных, J( ^ ) - матрица Якоби.

Для сравнительного анализа прогнозной точности описанных выше моделей рассмотрена выборка, состоящая из 5000 объектов, принимающих на каждом шаге одно из 14 возможных состояний. На основе данных, имеющихся за 17 шагов, строится прогноз состояний на следующем шаге и сравнивается с фактическими данными.

В результате применения нелинейных моделей погрешность прогноза составила менее 10%. При применении модели, содержащей факторы, учитывающие предыдущие переходы более одного шага, результат ухудшается. Следовательно, в рассматриваемом примере имеет смысл использовать нелинейную логистическую модель, содержащую лишь факторы внешнего воздействия (маргинальная модель), либо логистическую модель с учетом одного дополнительного фактора (модель 1-го порядка), отвечающего за переход на предыдущем шаге. На рис. 1 и 2 показано сравнение опытных и прогнозируемых данных на основе первых 500 исследуемых объектов.

Исследование выполнено при поддержке Министерства образования и науки Российской Федерации, соглашение 14.B37.21.0672 (федеральная целевая программа “Научные и научно-педагогические кадры инновационной России”).