Сравнительный анализ верифицированного численного моделирования кавитации на основе модели Рэлея – Плессета к насосам ТНА жидкостного ракетного двигателя

Работа турбонасосного агрегата (ТНА) в составе жидкостного ракетного двигателя (ЖРД) отличается повышенными требованиями к обеспечению работоспособности и поддержанию основных параметров при заданном ресурсе. Основное назначение ТНА – обеспечение непрерывной подачи компонентов топлива в камеру сгорания двигателя. На обеспечение работы ТНА может повлиять ряд факторов, например, локальное понижение давления жидкости, возникающее при обтекании профиля лопатки насоса. Данная область насоса может являться местом зарождения кавитации. Кавитацией называют фазовый переход жидкости в газ внутри жидкости при определенных температуре и давлении, который возникает в движущейся жидкости вследствие местных понижений давления до давления насыщенного пара. Нестабильность работы ТНА при кавитационном режиме за счет нарушения режима сплошности среды может повлиять на КПД и создаваемый удельный импульс ракетного двигателя [1].

При проектировании ТНА возникает необходимость проведения ряда модельных испытаний с целью отработки параметров насоса, а также подтверждения антикавитационных качеств насосов. Отработка режимов работы насоса при воздействии кавитации может проводиться как на испытательных установках с отработкой на модельной жидкости, так и при помощи различных методов численного моделирования в программах вычислительной гидродинамики (CFD).

На данный момент представлено достаточно большое количество различных программных пакетов, позволяющих численно смоделировать кавитацию при обтекании лопаток насосов, турбин, гидрокрыла водного судна или же при течении жидкости в различных сложных геометриях. Моделирование кавитационного потока может хорошо дополнить натурные испытания. Однако, несмотря на большую базу данных по уже проведенным испытаниям, повышенная энергонапряженность ТНА, как агрегата ЖРД, ставит вопрос об аппроксимации текущих данных к моделированию течения в насосе.

В пакете ANSYS для моделирования кавитационного течения представлен ряд моделей, основанных на уравнении Рэлея – Плессета. В данной работе рассматриваются результаты, основанные на применении модели кавитации Zwart – Gerber – Belamri, совместимой со всеми доступными в пакете ANSYS моделями турбулентности. Как и все модели физического явления, она обладает рядом ограничений [2]:

• –    предполагается, что происходит массообмен между жидкой и паровой фазами. В модели кавитации учитывается как образование пузырьков (испарение), так и схлопывание (конденсация);

• –    модель кавитации учитывает рост одиночного пузырька пара в жидкости;

• –    модель по умолчанию не учитывает влияние неконденсирующихся газов.

Теоретическая модель

Перед анализом данных рассмотрим уравнения, входящие в модель Zwart – Gerber – Belamri, основанные на уравнении Рэлея – Плессета. Впервые данное уравнение, описывающее полное превращение работы (совершаемой массой при схлопывании каверны) в кинетическую энергию, было представлено в работе [3]:

^pl RR TT

⁺ 2 R T

- p ,

где p – давление; R – радиус пузырька; ρ – плотность жидкости вокруг пузырька пара; R_T и R_TT – производные радиуса по времени. В работе [4] Плессет привел уравнение, описывающее рост газового пузырька в жидкости и выводимое из уравнений моментов:

, d² R B , 3 ( dR B ) ,  2 o _ Pv - p

-D ~ +             +                   , dt2    2 ( dt )   p f RB    p f где RB – радиус пузырька; pv – давление в пузырьке (предполагается, что это давление пара при температуре жидкости); p - давление в жидкости, окружающей пузырь; pf - плотность жидкости; σ – коэффициент поверхностного натяжения между жидкостью и паром.

В программном пакете ANSYS данная модель упрощается [2]. В ней не учитывается сила поверхностного натяжения и все уравнения второго порядка, так как данные уравнения используются для низкочастотных колебаний d ^ B — 2 Pv - P dt 3  p f

Именно данную модель рассматривали авторы Philip J. Zwart, Andrew G. Gerber, Thabet Be-lamri в статье [5]. Выражая через N B количество пузырьков, объемную долю пара на единицу объема можно выразить как

4 з

rv — VbNb — 3 nRB Nb , где RB – радиус пузырька в жидкости. Общая скорость межфазного массопереноса из-за кавитации на единицу объема будет равна

= 3 r v p v 1 2 P v - P R b P P l

Для случая конденсации уравнение выражается следующим образом:

S iv = F

3rv Pv / 2 Pv - P Rb V  Pi

sign ( P v — P ),

где F – эмпирический калибровочный коэффициент. Предполагая, что кавитационные пузырьки не взаимодействуют друг с другом, авторы статьи [5] заменили r v на r nuc (1 – r v ) для случая испарения, где r nuc – объемная доля центра образования пузырьков кавитации. Окончательный вид модели кавитации:

S iv = "

F    r nuc (1   r v ) P v 2 Pv_P if P <  P , vap       RB       33   pz    j        v’ Bl          (7) P   S r v P v 2 P - P v 1 cond n л о           f >  vv . t        R B  V3 p i

Для данной модели применяются следующие значения: R B = 10^–6 м, r nuc = 5 ∙ 10^–4, F vap = 50 и F cond = 0,01.

Вышеописанная модель кавитации включается в уравнение переноса пара:

d         —

—(apv) + V(aPvVv) = Re -R, о t где α – объемная доля пара; ρν – плотность пара; Vν – скорость паровой фазы; Re, Rc – источники массообмена, связанные с ростом и схлопыванием пузырьков пара соответственно (моделируются на основе уравнения Рэлея – Плессета).

Также рассмотрим уравнения, входящие в модель турбулентности. Известно, что течение жидкостей и газов в природе можно разделить на два вида: ламинарное и турбулентное. Если первое течение характеризуется стабильностью параметров или, в крайнем случае, плавностью их изменения, то для турбулентного течения П. Брэндшоу приводит следующее определение турбулентности [6]: «Турбулентность – это трехмерное нестационарное движение, в котором вследствие растяжения вихрей создается непрерывное распределение пульсаций скорости в интервале длин волн от минимальных, определяемых вязкими силами, до максимальных, определяемых граничными условиями течения. Она является обычным состоянием движущейся жидкости, за исключением течений при малых числах Рейнольдса».

В основе моделей турбулентного потока, используемых в ANSYS, лежит теория Л. Прандтля и работы А. Н. Колмогорова. Теория Прандтля основана на вычислении смещения потока через отношение скорости переноса количества движения между соседними слоями к длине элементарной площадки, причем скоростью переноса служит поперечная пульсационная скорость. Колмогоров в статье [7] предложил систему уравнений для турбулентного режима, легшую в основу описываемой далее модели. В статье [8] авторы B. E. Launder и D. B. Spalding описали модель турбулентности, основанную на системе из уравнения для кинетической энергии турбулентности k :

d ( p k ) d t

d d

+—(p uik) = —

O X i           O X j ^

Ц

ц t dk

о k J 5xj

+ G k + G b

- Pe- YM + Sk.

Уравнение для значения e (скорость диссипации энергии турбулентности) можно получить из уравнения Навье – Стокса, но данное уравнение получается незамкнутым. Для замыкания необходимо представить уравнение в следующей записи:

d(pe) + 5(pe u)

5 t       5 x i

5 Г ш ) de -- ц + — I-- 5xj ( ^Jdxj

+ C e i ( G k + C 3 e G b ) - C _E 2 P- + 5 _E . k

В данных уравнениях, μ t = ρ C μ k ²/ε – коэффициент турбулентной вязкости; G k – прирост кинетической энергии турбулентности из-за градиентов средней скорости; G_b – прирост кинетической энергии турбулентности за счет плавучести; Y M – вклад флуктуирующей дилатации в сжимаемой турбулентности в общую скорость диссипации. C ε1 , C ε2 и C ε3 – константы; σ k и σ ε – турбулентные числа Прандтля для k и ε соответственно; S k и S ε – задаваемые значения. В ANSYS [2] для констант принимаются следующие значения: C ε1 = 1,44, C ε2 = 1,92 и C μ = 0,009, σ k = 1,0 и σ ε = 1,3.

Важно отметить, что в статье [5] обращается внимание на то, что стандартные модели турбулентности не могут правильно предсказать колебательное поведение потока. Для этого авторы использовали модифицированную формулу коэффициента турбулентной вязкости

Ц tm = f (P) Cц —, (11) e гДе f(P) = Pv + ((Pv -Pm ) / (Pv - Pi))n • (Pi - Pv ).

Рассмотрение статистики по испытаниям различных насосов

Необходимо отметить, что в рассматриваемых геометрических моделях не применялся преднасос для повышения антикавитационных качеств насоса (в статье [9] он применялся при эксперименте, но не в модели). В модельных испытаниях ТНА ЖРД преднасос устанавливался, что также необходимо отразить в геометрической модели при численном моделировании кавитационного потока.

В статье [5], в которой впервые представлена модель Zwart – Gerber – Belamri, авторы также рассматривают применение данной модели к геометрии, схожей с рассматриваемыми насосами (случай кавитации в преднасосе). Проводится сравнение экспериментальных данных с моделированием. Авторы отмечают, что вблизи номинального режима работы (Q / Qn = 1,03), падение напора на кривой происходит быстрее и одновременно с экспериментальными измерениями.

В статье [9] авторы рассматривают вопрос численного моделирования колебаний в центробежном насосе при малом расходе. В качестве модели турбулентности применяется модель RNG k-ε. Расчетные параметры также приведены в таблице. Результаты гидравлических испытаний показаны на рис. 1. Авторы проводят расчёты в среде ANSYS CFX с числом ячеек 1562765, а также проводят сравнение полученных напоров H при числах ячеек 1562765, 1837613, 2129429, 2375885, 2629005. Напор при числе ячеек 1562765 отличится от напора при числе ячеек 2629005 в 1,008535 раза, что говорит о малом влиянии числа ячеек на точность расчета, при превышении их суммы определённого предела.

Значение NPSH (Net Positive Suction Head) на рис. 1 – чистый гидравлический напор или кавитационный запас, измеряемый высотой столба жидкости на входе в насос, NPSHa – располагаемое значение напора на входном патрубке насоса за вычетом давления насыщенного пара жидкости

NPSHa = p^- + uin - p^-, (12) Pig 2 g Pig где pin – давление на входе в насос; иin – скорость на входе в насос; pν – давление насыщенного пара.

В статье [10] авторы берут за основу для сравнения данные гидравлического пролива спроектированного центробежного насоса, расчетные параметры для которого представлены в таблицe. В качестве модели турбулентности выбирают модель турбулентности RNG k-ε, модифицированную на основе идеи Йохансена. Полученные параметры для номинального режима представлены на рис. 2. Анализ параметров показывает хорошую сходимость экспериментальных данных с результатами моделирования. Причинами же расхождения авторы считают:

• –    отсутствие учета зазора между лопатками и корпусом, потерь на расширения воды в коллекторе выхода;

• –    принятые допущения в доступной модели кавитации.

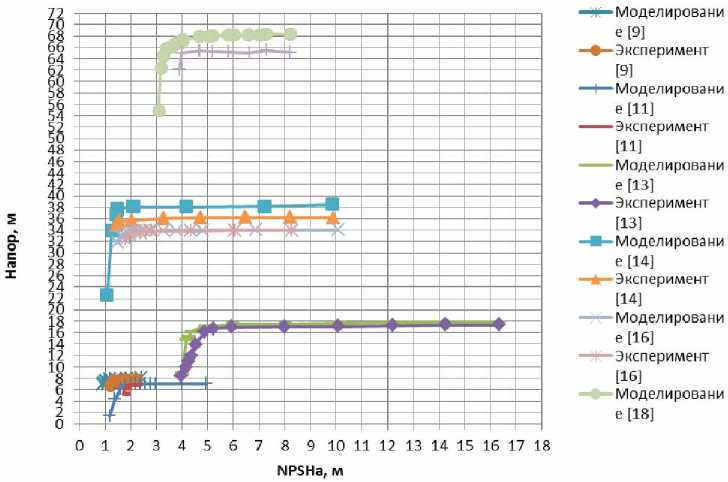
Рис. 1. Сводный график напоров

• Fig. 1.    Summary head graph

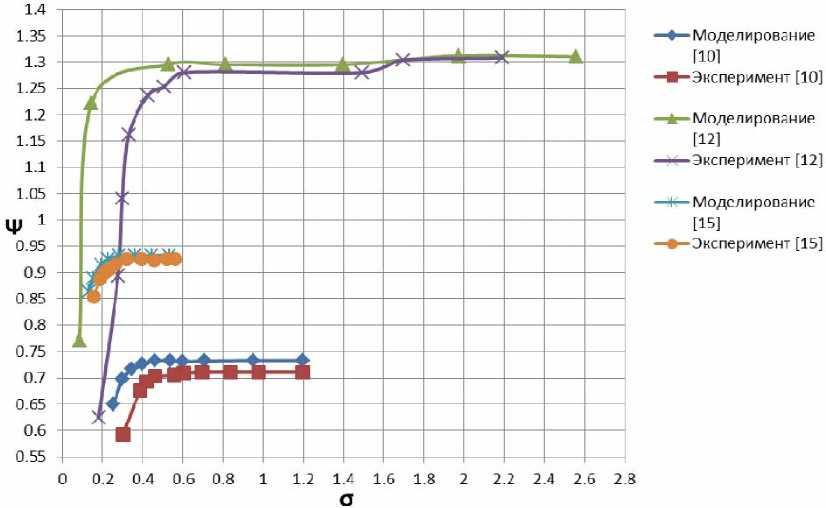
Рис. 2. Сводный график чисел кавитации

• Fig. 2.    Summary graph of cavitation numbers

Значение Ψ – коэффициент напора, выражается формулой

H

^Ψ    u 2 ^{2 ,}

2g где H – напор насоса; u2 – окружная скорость на выходе. Число кавитации σ выражается формулой pin - pv σ= in v .

0,5 ρ _lu ₂ ²

В статье [11] исследуются колебания давления в насосе при кавитационном режиме. В качестве модели турбулентности используется модель RNG k-ε. В работе приведена геометрическая модель насоса, аналогичная модели из статьи [9], но режим работы рассматривался при номинальном расходе. Данные о результатах реального эксперимента и численного моделирования приведены на рис. 1. Используемая для расчетов сетка состоит из 1,56 млн элементов.

В статье [12] также исследуются кавитационные явления в центробежном насосе. В качестве модели турбулентности применяется модель SST k-ε. При исследовании, авторы выбрали модель центробежного насоса с малым значением коэффициента быстроходности, расчетные параметры которого приведены в таблице. Результаты гидравлических испытаний показаны на рис. 2 (значение Ψ было рассчитано по имеющимся данным в статье, так как в статье приводится только значение напора). Используемая для расчетов сетка состоит из 1180228 элементов.

В статье [13] исследуется влияние кавитации на производительность насоса. Авторы выбрали для исследования насос АР1400, отличающийся высокими показателями расхода. Используемая модель турбулентности – RNG k-ε. Данные о результатах реального эксперимента и числового моделирования также приведены на рис. 1. Расчетная сетка состоит из 5,9 млн элементов.

В статье [14] исследуется производительность и кавитационное течение в насосе. Авторы использовали геометрическую модель насоса, расчетные характеристики которого представлены в таблице. В качестве модели турбулентности применяется модель SST k-ε. График численного моделирования и эксперимента представлен на рис. 1 (в работе [14] по оси y указано отношение напоров, для графика взято значение напора из статьи, умноженное на Н d ). Расчетная сетка состоит из 3,02 млн элементов.

В статье [15] проводится исследование влияния кавитации на усовершенствованную лопатку колеса насоса. Авторы использовали геометрическую модель насоса, расчетные характеристики которого представлены в таблице. График численного моделирования и эксперимента представлен на рис. 2. Авторы также провели сравнение полученного напора при различном числе элементов в геометрической модели: 5, 9,1, 12 и 20 млн. Результаты показывают максимальное отклонение коэффициента напора в 1,12 %. Используемая сетка состоит из 12 млн элементов.

В статье [16] исследуется вопрос моделирования кавитации в насосе. В качестве модели турбулентности применяется модель SST k-ε. График численного моделирования и эксперимента представлен на рис. 1. Аналогично рассмотренной ранее работе [14], в работе [16] по оси y указано отношение напоров. Для графика на рис. 1 взято значение напора из статьи, умноженное на Н d . Расчетные характеристики насоса представлены в таблице. На основании работ, проведенных авторами в [17], утверждается об относительной независимости решения от количества элементов сетки. В связи с этим, в расчетной модели насоса в статье [16] используется сетка из 5207832 элементов. Авторы также заявляют о хорошей сходимости практических результатов с результатами моделирования.

В статье [18] рассматривается кавитация в насосах двустороннего входа. Данное исполнение рабочего колеса насоса также применяется и при проектировании ТНА для ЖРД ракет. Авто- рами выбран для исследования насос двустороннего входа ES8-300KPS. В качестве модели турбулентности применяется модель k-ε. График численного моделирования и эксперимента представлен на рис. 1, расчетные характеристики насоса двустороннего входа представлены в таблице. Расчетная сетка состоит из 4198349 элементов.

Сравнительная таблица насосов

№ п/п	Статья/ насос	Наименование характеристики	Значение параметра
1	Спроектированный насос из статьи [10]	Номинальный расход	32,8 м3/ч
		Коэффициент быстроходности	135
		Угловая скорость	1450 об/мин
		Число лопаток	5
		Внешний диаметр D2	0,169 м
		Ширина колеса на выходе	0,014 м
2	Спроектированный насос из статьи [9] и [11]	Номинальный расход	25 м3/ч
		Напор	7 м
		Угловая скорость	1450 об/мин
		Число лопаток	7
		Внутренний диаметр D1	50 мм
		Внешний диаметр D2	160 мм
3	Спроектированный насос из статьи [12]	Номинальный расход	8,6 м3/ч
		Коэффициент быстроходности	32
		Угловая скорость	500 об/мин
		Число лопаток	6
		Внешний диаметр D2	310 мм
		Внутренний диаметр D1	80 мм
4	Насос АР1400 [13]	Номинальный расход	1385 м3/ч
		Напор	17,8 м
		Угловая скорость	1485 об/мин
		Число лопаток	18
5	Спроектированный насос из статьи [14]	Номинальный расход	25 м3/ч
		Напор	36 м
		Коэффициент быстроходности	60
		Угловая скорость	2900 об/мин
		Число лопаток	5
		Внешний диаметр D2	172 мм
		Внутренний диаметр D1	65 мм
		Ширина колеса на выходе	12 мм
6	Спроектированный насос из статьи [15]	Номинальный расход	200 м3/ч
		Напор	20 м
		Угловая скорость	1450 об/мин
		Число лопаток	6
		Внешний диаметр D2	270 мм
		Внутренний диаметр D 1	150 мм
		Ширина колеса на выходе	30 мм
7	Спроектированный насос из статьи [16]	Номинальный расход	50 м3/ч
		Напор	34 м
		Угловая скорость	2900 об/мин
		Число лопаток	6
		Коэффициент быстроходности	88,6
8	Спроектированный насос ES8-300KPS из статьи [18]	Номинальный расход	820 м3/ч
		Напор	64 м
		Угловая скорость	1480 об/мин
		Число лопаток	6

Рассмотрим графики на рис. 1. Если принять за начало кавитации 3 % падение напора, то можно сделать следующие выводы.

• 1.    Начало кавитации для моделирования фиксируется при меньшем значении NPSHa по сравнению с экспериментом, но большем напоре для [9; 13; 14; 16; 18].

• 2.    Начало кавитации для моделирования фиксируется при большем значении NPSHa по сравнению с экспериментом и большем напоре для [11].

• 3.    В точке начала кавитации отличие NPSHa относительно эксперимента меньше для статей [9] на 10 %, [13] на 6 %, [14] на 6 %, [16] на 15 %, [18] на 10 %.

• 4.    В точке начала кавитации отличие NPSHa относительно эксперимента больше для статьи [11] на 6 %.

• 5.    В точке начала кавитации отличие напоров относительно эксперимента больше для статей [9] на 5 %, [11] на 3 %, [13] на 2 %, [14] на 6 %, [16] на 0,3 %, [18] на 4,5 %.

Также рассмотрим графики на рис. 2. Если принять за начало кавитации 3 % падение напора, то можно сделать следующие выводы:

• 1.    Начало кавитации для моделирования фиксируется меньшем значении σ, но большем Ψ для [10; 12; 15].

• 2.    В точке начала кавитации отличие σ относительно эксперимента меньше для [10] на 18 %, [12] на 62 %, [15] на 8 %;

• 3.    В точке начала кавитации отличие Ψ относительно эксперимента больше для [10] на 3 %, [12] на 0,2 %, [15] на 0,7 %.

Заключение

По результатам рассмотрения упомянутых работ, представленных выше графических материалов и данных о расчетных сетках можно сделать следующие выводы:

• 1.    Численное моделирование кавитационного потока показывает удовлетворительную сходимость для значений напоров насосов. Данные показатели остаются стабильными и для больших значений напора. Расхождение параметров при моделировании кавитации в насосе двустороннего входа аналогичны расхождению параметров для моделей с одним входом.

• 2.    Данные по значениям σ и NPSHa относительно напора отличаются в худшую сторону, так как некоторые работы показали большое расхождение экспериментальных данных и данных моделирования течения.

• 3.    Число элементов сетки оказывает меньшее влияние на точность численного моделирования, так как отличие моделей с большим и меньшим числом ячеек незначительно.

Упомянутые выше выводы необходимо учитывать при применении модели Zwart – Gerber – Belamri для численного расчета гидравлического кавитационного потока в наосах ТНА ЖРД.