Сравнительный анализ влияния аддитивных помех на сигналы, модулированные вейвлет-функцией и фазоманипулированные сигналы

чением времени, наряду с развитием радиоэлектронной техники, она будет обостряться еще больше. Изучение видов помех помогает эффективней бороться с ними и создавать более совершенные с точки зрения помехозащищенности системы радиосвязи.

Помеха – это возмущающее воздействие, препятствующее правильному приёму и оцениванию параметров сигнала. Источники помех могут находиться как вне, так и внутри самой системы.

По воздействию на полезный сигнал выделяют аддитивные и мультипликативные помехи.

Аддитивная помеха проявляет себя независимо от сигнала. Передаваемый сигнал a ( t ) подвержен воздействию аддитивного шумового процесса n ( t ). Физически аддитивный

■_■ ИССЛЕДОВАНИЯ

Havko-

Ограда

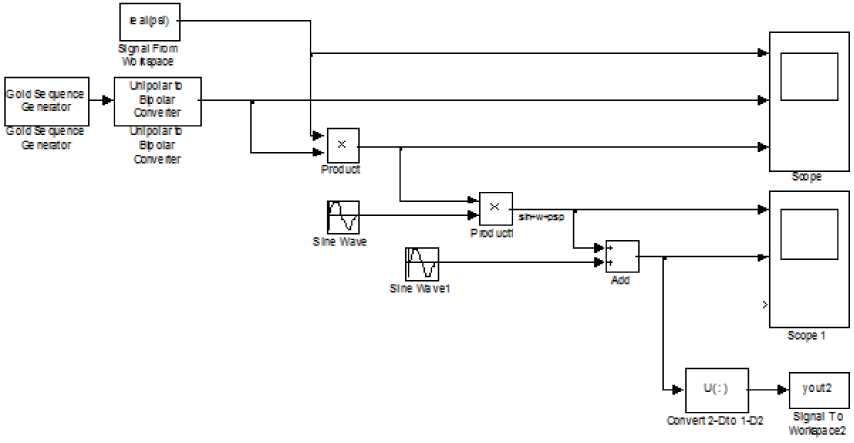
Рис. 1. Блок-схема для моделирования воздействия аддитивной помехи на сигнал, модулированный вейвлет-функцией

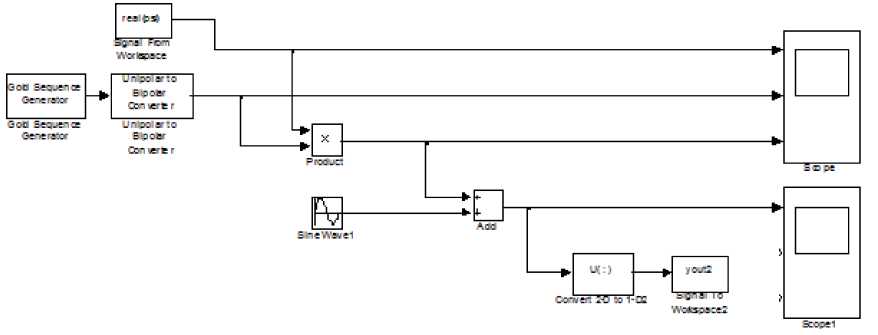
Рис. 2. Блок-схема для моделирования воздействия аддитивной помехи на фазоманипулированный сигнал

В. А. Анжина, А. А. Клушин

Сравнительный анализ влияния аддитивных помех на сигналы, модулированные вейвлет-функцией шум возникает от посторонних электрических помех, электронных компонентов и усилителей в приёмнике систем связи, а также из-за интерференции сигналов.

Если шум обусловлен в основном электронными компонентами и усилителями в приёмнике, его можно описать как тепловой шум. Этот тип шума характеризуется статистически как гауссовский шумовой процесс. Как следствие, результирующую математическую модель обычно называют каналом с аддитивным гауссовским шумом. Поскольку эта модель применима к широкому классу физических каналов связи и имеет простую математическую интерпретацию, она является преобладающей моделью канала при анализе и синтезе систем связи. Затухание каналов легко включается в модель. Если при прохождении через канал сигнал подвергается ослаблению, то принимаемый сигнал

s(t) = α a(t) + n(t), где α – коэффициент затухания линейного канального фильтра.

Мультипликативная помеха возникает только при наличии сигнала. Природа этой помехи состоит в случайном изменении параметров сигнала. Случайная функция n ( t ) перемножается с полезным сигналом, поэтому её можно рассматривать как функцию, модулирующую по амплитуде излучённый сигнал. Модуляция приводит к расширению спектра принятого сигнала относительно спектра излучённого сигнала. Поэтому такой канал называют каналом с рассеянием энергии по частоте:

s ( t ) = a ( t ) ∙n ( t ).

По времени корреляции мультипликативные помехи разделяются на медленные и быстрые. О медленных замираниях говорят в случае, если время корреляции n(t) значительно превышает интервал наблюдения сигнала. Причинами медленных замираний являются изменения свойств среды распространения ра- диоволн в зависимости от метеорологических условий, времени суток, года, от солнечной активности и т.п. Быстрая мультипликативная помеха имеет время корреляции меньше, чем интервал наблюдения сигнала. Основной причиной быстрых замираний является наличие многих путей, по которым распространяются электромагнитные волны. Многолучевое распространение возникает при передаче информации на дальние расстояния при отражении радиоволн от протяженных поверхностей суши и моря, при отражении от ионосферы и 15 тропосферы. Из-за разных путей распространения время запаздывания отдельных принимаемых сигналов различно. Поэтому многолучевые каналы называют также каналами с рассеянием энергии во времени.

Рассмотрим влияние аддитивной помехи на спектр передаваемого сигнала. В качестве аддитивной помехи возьмём синусоиду с несущей частотой 1,646 ГГц, т.е. такой же частоты, как и несущая полезного сигнала.

Блок-схема для моделирования воздействия аддитивной помехи на сигнал, модулированный вейвлет-функцией, изображена на рис. 1.

Блок-схема для моделирования воздействия аддитивной помехи на фазоманипули-рованный (ФМ) сигнал изображена на рис. 2.

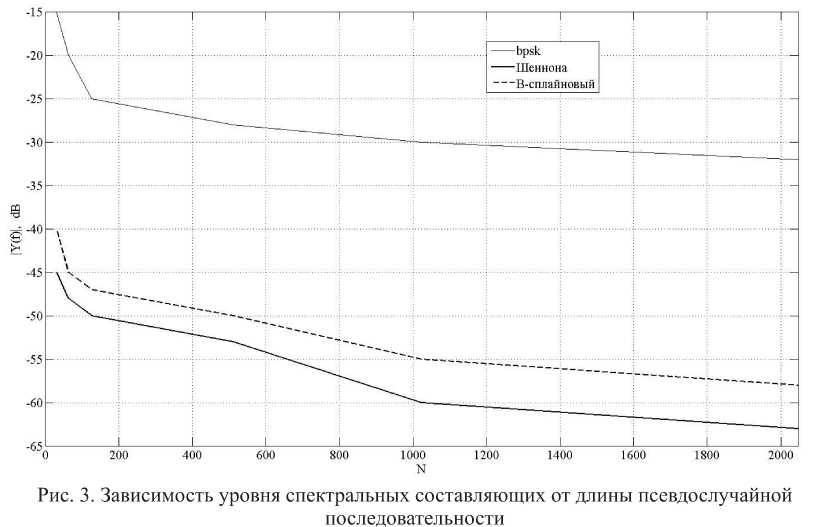
Для сравнения представим полученные результаты на одном графике (рис. 3).

Результаты исследований показали, что влияние аддитивной синусоидальной помехи на ФМ-сигнал более значительное, чем на сигнал, модулированный вейвлет-функцией. Сигнал, модулированный вейвлет-функцией, обладает большей шириной спектра, следовательно, и наилучшей помехозащищённостью.