Сравнительный анализ жесткости двух схем арочной фермы

Основные задачи в статике стержневых систем – это задачи о прочности и жесткости. Особую роль в исследованиях ферм играют точные аналитические решения, служащие с одной стороны тестовыми оценками численных методов, с другой – позволяющие провести анализ конструкции с целью выявить ее особенности и оптимизировать размеры фермы. Современные системы компьютерной математики (Maple, Mathematica, Maxima и др.) позволяют выполнить решение в символьной форме и получить, например, значение прогиба как функцию параметров конструкции, куда входят геометрические размеры, характеристики материала, нагрузка. Однако ввести в параметры задачи число панелей или число стержней фермы значительно сложнее. Единственный путь в этом случае – применить метод индукции, состоящий в решении последовательности ферм с различным числом панелей и выявлении закономерности образования коэффициентов в соответствующих формулах. Метод индукции совместно с возможностями системы Maple [1-3] применим как в расчетах плоских [4-8], так и пространственных [9-14] регулярных стержневых систем.

Аналитические решения для прогиба плоской статически определимой арочной фермы, являющейся аналогом широко применяемой в покрытиях портовых сооружений схемы стропильной фермы «Молодечно», получено в [4]. На кривой зависимости прогиба от числа панелей обнаружен минимум и точка перегиба. Рассмотренная в этой работе схема фермы отличается большим подъемом, что заметно увеличивает высоту рабочего помещения. Размеры фермы определяются двумя геометрическими параметрами и числом панелей. В [5] исследованы усилия в стержнях плоской один раз статически неопределимой решетчатой ферме. Показано, что ферма с четным числом панелей геометрически изменяема, даже при наличии лишнего стержня. Найдена и проанализирована формула для прогиба. Примененный в [4,5] метод индукции оказался работоспособным и в анализе стержневой системы крепления микромеханического гироскопа [6]. Более простые схемы фермы, нагруженные одной сосредоточенной в середине пролета силой, исследованы в аналитической форме в [7,8]. Получение аналитических формул для прогиба пространственных ферм сложнее, и такие решения встречаются реже [9,10]. В основном в этом случае используются численные методы [11-14]. В последнее время стали применяться и методы искусственного интеллекта [15-17]. Поиск простых решений для регулярных статически определимых (плоских и пространственных) стержневых систем, вероятно, впервые начал Hutchinson R. G.[18-19]. Именно он, предложив новые и исследовав некоторые существующие фермы, объявил «охоту» на схемы статически определимых регулярных ферм. Охота продолжается! Одна из таких ферм предлагается в настоящей работе. Для сравнения в аналитическом виде рассчитывается известная схема фермы.

2.    Две схемы фермы

Схема 1. Рассмотрим арочную статически определимую ферму с крестообразной решеткой, нагруженную равномерно по верхнему поясу (рис.1). Одна опора фермы – неподвижный шарнир, друга – подвижный. Фактически эта ферма состоит из двух простых ферм с крестообразной решеткой, соединенных шарниром и горизонтальным стержнем в середине пролета. Подъем фермы определяется длиной этого стержня. Ферма принадлежит к безраспорному типу. Конструкция узлов фермы предполагает, что стержни крестообразной решетки лежат в разных плоскостях, а плоская идеализация незначительно искажает картину напряженного состояния в стержнях.

В ферме, состоящей из 2 n панелей, содержится 4 n +1 шарниров и 8 n +2 стержней, включая три стержня, которые моделируют опоры. Эти стержни в расчете будем полагать жесткими. Усилия в стержнях определяем методом вырезания узлов.

Construction of Unique Buildings and Structures, 2015, №9 (36)

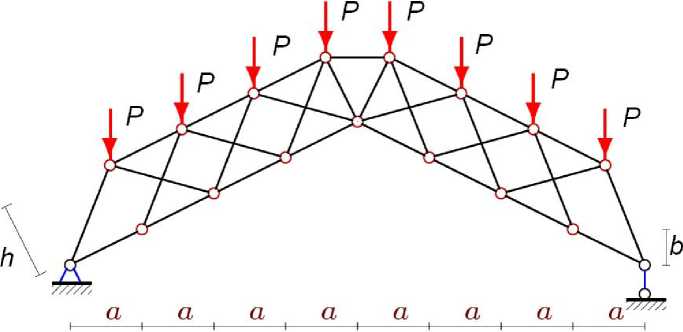
Рисунок 1. Схема 1 фермы, n=4, a=h=2b

Для ввода информации о геометрии фермы в программу системы Maple [1] пронумеруем шарниры сначала по нижнему, затем по верхнему поясу. Начало координат выберем в левой неподвижной опоре. Имеем следующие координаты узлов:

xi = ai - a, i = 1,...,2n +1,

yi = (i -1)b, i = 1,...,n +1, yi = (2n +1 - i)b, i = n + 2,..., 2n +1,

xi+2n+1 = ai - d, yi+2n+1 = f + bi,

xi+3 n+1 = a (n - 1 + i) + d,

yi+3n+1 = y3n+2-i, i = 1,---,n,

где d = bh I c, f = ah I c, c = a2 + b2, (рис. 2).

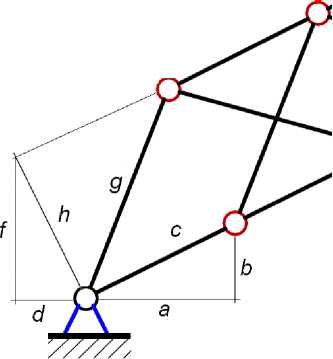
Рисунок 2. К выводу геометрических соотношений

Структуру соединения стержней и шарниров введем условными векторами V i , i = 1,..., m . В этих векторах первая компонента – номер шарнира фермы в начале вектора, вторая – номер шарнира в его конце. Направление вектора-стержня не связано с усилием в этом стержне и служит лишь для определения схемы соединений в ферме, что необходимо для записи уравнений равновесия узлов в проекции на оси координат.

Имеем следу ю щие векторы:

• •    нижний пояс Vi = [i,i + 1], i = 1,...,2n,

• •    верхний пояс Vt+2n = [г +1 + 2n,i + 2 + 2n], i = 1,...,2n — 1,

• •    решетка Vi+4n-1 = [i,i + 2n +1], Vi+5n-1 = [i + n +1,i + 3n +1], i = 1,..., n,

Vi+6n—1 = [i + 2,i +_2n +1], V+7n—2 = [i + n,i + 3n + 2], i = 1,...,n — 1.

V8 n-2 = [1 + n ,1 + 3 n ], V8 n—1 = [1 + n ,2 + 3 n ].

Косинусы углов усилий в уравнениях равновесия узлов фермы вычисляются через длины стержней и проекции условных векторов стержней на оси координат li = Vl1,i2 + 12,i2 , l1,i = xV2,i — xV1ii ’ 12ii = yV2,, — yVx,,' i = 1,—,m, где m = 8n + 2 - число стержней фермы. Первый индекс (1 или 2) в номере Vj i соответствует номеру компоненты вектора Vi , второй – номер стержня. Матрица G направляющих косинусов имеет следующие элементы:

• G, .= — 1./1, k = 2V 7— 2 + j, k < m, j = 1,2, i = 1,..., m,

rv , i            j , i      i                    i ,2

G, .= 1 ./1, k = 2V,— 2 + j,  k < m, j = 1,2, i = 1,..., m.

k , I        j , I      I                    1 ,1

Заметим, что предложенный способ задания геометрии и структуры фермы не единственный. Известен также метод матрицы инциденции [21], однако этот способ (ранее широко применявшийся в расчетах ферм) значительно более трудоемкий и менее наглядный. Эти два способа сравнимы между собой также как в теории графов сравнимы способ задания графа списком ребер и с помощью матрицы и н циденции. Известно, что список ребер (аналог использованному здесь векторному способу с векторами V _i ) задает граф проще.

Усилия в стержнях фермы определяются из решения системы линейных уравнений в матричной форме

G 5 = B, где S – вектор неизвестных усилий, B – вектор нагрузок длиной m. Значения горизонтальных нагрузок, приложенных к узлу i, находятся в нечетных элементах B2i—1, значения вертикальных нагрузок-в четных B2i. Решение находим с помощью обратной матрицы 5 = G 1B . Этот метод особенно удобен в том случае, когда одну и ту же систему приходится решать несколько раз. Здесь система решается дважды – один раз с внешней нагрузкой, другой – с единичной силой, приложенной в середине пролета. Метод обратной матрицы хорошо реализуется в системе Maple.

Прогиб определим по формуле Максвелла-Мора, разделив сумму на три части:

8 n + 1 о( P ыт 2 n о( P ыт 4 n — 1 о( P Ы1)/  8 n + 1 о( P Ы1)/

д (1) = у ⁵i ⁵i ^li =у ⁵i ⁵i ^li + у   ⁵i ⁵i ^li + у ⁵i ⁵i ^li (1)

.

i = 1 EF i i = 1 EF 1 i = 2 n + 1 EF 2 i = 4 n EF 3

В первую сумму входят усилия в нижнем поясе, во второй – в верхнем, в третьей – в решетке. Использованы обозначения: S iP ) для усилия в стержне с номером i от действия внешней нагрузки, S i^¹ – для усилия в этом же стержне от действия единичной вертикальной нагрузки в середине пролета (узел с номером n +1). Принято, что жесткость всех стержней нижнего пояса равна EF 1 , верхнего - EF 2 , решетки - EF 3 . Разделение суммы на три части вызвано не только желанием получить более универсальную формулу для ферм, выполненных из стержней различной площади сечения, но и в силу математических трудностей, вызванных сложностью конечных формул. Методом индукции на основе обобщения аналитических расчетов в символьной форме ферм с числом панелей от 1 до 16 для стержней нижнего пояса было получено следующее выражение

Construction of Unique Buildings and Structures, 2015, №9 (36)

2 n ( P )c(1)/

S Sl

Ai=E i

m   EF 1

P

EF\

(

C i

V

2             ,         , 2 A ac ab b

IF + C'2h + C3 TJ

где

C = —(10 n4 + 8 n3 +14 n 11 48V

- 8n + 3 - 3(6n1 +1)(-1)n ),

Cг = -112 ( 20 n3 + 6 n 2 +16 n - 3 + 3(1 - 4 n )(-1)n),

C3 = n •

Аналогично, для верхнего пояса имеем:

C4 = (10n4 + 8n3 + 2n2 - 8n + 3 + 3(6n2 -1)(-1)n) / 96,

C5 = (8n3 - 6n2 - 2n + 3 + 3(2n -1)(-1)n) / 48,

C6 = n 2( n +1)/2,

4 n - 1 o( P W1),

Z o о

-i---i_A_ = 2

i = 2 n + 1    ^EF 2

P

EF2 V

(

^C 4

a ² c     ab

,2 ^C 5 , ^{+ C} 6 _h 2 _h

cb

h

6 2 ^

C3 - • aJ

Для стержней решетки:

C7 = (6 n2 +1 - (-1)n )/8,

C8 = (2n(-1)n - (-1)n +1)/4,

C9 = - n (n +1) / 2,

о8 P--2 = P( C8 a + C9 b + nb-V c h acJ

08n-2=- n ^h+2c «-1) ”- ц’

A3 =

8 n-1 o( P )o(1)z у oi oi li = i ^^!n   EF3

P C 7 g³ a ² EF₃ c ² h³³

( P )    (1)

+ ^o 8 n - 2 ^o 8 n - 2 ^h

EF 3

где g = cc ² + h ²

длина раскосов (рис. 2). В последнем случае отдельно выделены два стержня-стойки длиной h, так как выражения усилий в них отличались по форме от остальных усилий в решетке, что затрудняло нахождение закономерностей в коэффициентах решения.

Алгоритм определения коэффициентов C ^ , к = 1,...,9, разделялся на три этапа. Сначала в результате решения задачи получались последовательности коэффициентов, затем с помощью команды rgf_findrecur пакета genfunc системы Maple определялось рекуррентное уравнение, которому удовлетворяют эти коэффициенты. Решение же уравнения находил оператор rsolve. Символьные преобразования в системе Maple при значительном числе панелей занимают большое время. Численные вычисления в этой же системе выполняются почти мгновенно, поэтому проверка индукции была проведена численно с большими числами панелей. При этом было также обнаружено, что численные методы часто накапливают ошибки округления, что делает еще более ценными символьные результаты.

Construction of Unique Buildings and Structures, 2015, №9 (36)

Схема 2. Ферма с прямоугольной решеткой (рис. 3) имеет более простую конструкцию, содержит только два геометрических параметра и значительно проще для расчета [8]. Как и в схеме 1, здесь две опоры – подвижная и неподвижная. Подъем фермы определяется соотношением длин стержней. Независимо друг от друга выбираются длины вертикальных ( h ) и горизонтальных ( a ) стержней (в схеме 1 – три независимых размера). Наклонные стержни нижнего и верхнего пояса имеют длину V a ² + h ² . При a = h наклон поясов составляет 45 ° . В ферме c 2 n панелями содержится 4 n +2 шарниров и 8 n +4 стержней, включая три опорных стержня.

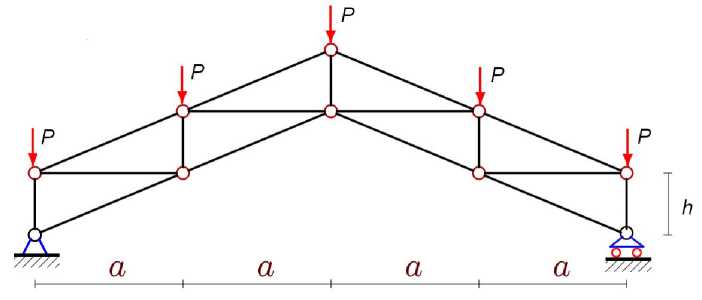
Рисунок 3 . Схема 2 фермы, n =2, a= 2 h

Опуская выкладки (они значительно проще, чем в схеме 1), запишем выражение для прогиба середины пролета фермы (жесткость стержней принята одинаковой):

8n+1 SjP)S^li  P n2(a3 + (2n +1)h3 + c3(1 + 5n2)/6) “ EF " EF          2 h2

Как и для схемы 1, суммирование производится здесь по деформируемым стержням.

3.    Сравнение и анализ

Пусть задана фиксированная длина пролета фермы, ее высота и суммарная нагрузка. Таким образом, длина панели a (как для схемы 1, так и для схемы 2) выражается по формуле a = L / (2 n ) . Размер в схеме 1: b = H / n , аналогично, в схеме 2: h = H / n . Таким образом, обе фермы имеют одинаковый пролет L и одинаковую высоту H , которая вычисляется по средней точке нижнего пояса. Нагрузка на узел имеет вид P _ P sum / ( n + 1) . Введем обозначение для относительного прогиба А _ N EF / P . Предположим, что жесткости стержней в схеме 1 одинаковые EF _ EF-, = EF-, и

SUfm                                        12   3

совпадают с жесткостью стержней фермы 2. Вычисления по формулам (1) и (2) дают кривые, представленные на рисунке 4. При этом оказывается, что для большого числа панелей предлагаемая схема 1 более жесткая.

Construction of Unique Buildings and Structures, 2015, №9 (36)

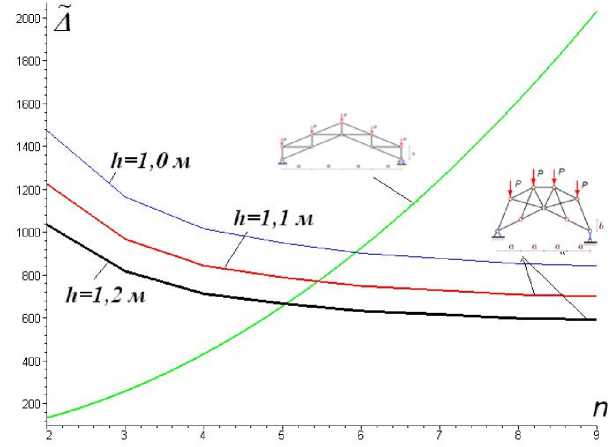
Рис. 4. Зависимость прогиба от числа панелей. L = 30 м , H = 6 м

Прогиб фермы 1 падает с увеличением числа панелей, фермы 2 – растет. Принципиально различное поведение кривых прогиба ферм 1 и 2 можно проверить из предельного анализа:

f^v lim А 1 = 0, n ^^

^^

5( L ² + 4 H ²)³ / ² 192 H ²

^А2 lim —2 = n ^^m П

Прогиб фермы 2 растет по квадратичному закону. Увеличение параметра h закономерно приводит к уменьшению прогиба фермы 1.

4.    Заключение

Методом индукции выведены формулы для прогиба арочных ферм. Первая схема – трехпараметрическая (независимые размеры a, b, h ), вторая содержит только два параметра. В первом случае решение заметно более сложное, хотя как и решение для второй схемы, выражается полиномами по числу панелей. Кроме того, рассмотренные схемы фермы показали принципиально разные зависимости прогиба от числа панелей. На этом примере особенно четко выявилось преимущество аналитических решений перед численными. Не умаляя роль численных методов, позволяющих учесть все возможные особенности конструкции, отметим роль символьной математики для теоретической оценки проектируемых конструкций. Именно аналитические методы позволяют выявить существенные особенности конструкций и упредить возможные ошибки проектирования, найти способы оптимизации, получить оценочные значения решений. Особую роль здесь играет индуктивный метод, разработанный как для пространственных, так и для плоских стержневых конструкций.