Среднеквадратическая ошибка фильтрации как критерий обнаружения аномалий сетевого трафика

Известно, что сетевой трафик обладает свойством самоподобия, или фрактально-сти. Этим свойством могут обладать интервалы времени между поступлениями пакетов (inter-arrival times) либо суммарное количество пакетов (или байт) в единицу времени. Самоподобие предполагает наличие автокорреляционной функции (далее – АКФ) определенного вида. Так, в работе Ли [1] проводилось исследование трассировок трафика на транзитном канале к вышестоящему интернет-провайдеру, предоставленного MAWI

Среднеквадратическая ошибка фильтрации как критерий обнаружения аномалий ...

Плаван Алексей Игоревич аспирант кафедры информационной безопасности, Поволжский государственный университет телекоммуникаций и информатики, город Самара. Сфера научных интересов: анализ и моделирование сетевого трафика; обнаружение вторжений; статистический анализ. Автор более 10 научных публикаций. ORCID: 0000-0002-4911-7459, ResearcherID: HGB-2716-2022, SPIN-код: 1130-6500.

(Measurement and Analysis on the WIDE Internet) Working Group1 и собранного в период с 1 января 2007 года по 31 декабря 2018 года. Было показано, что АКФ ежедневного трафика на этом интервале времени может быть аппроксимирована АКФ процесса Коши. Соответственно, можно предположить, что ожидаемый трафик некоторой сети в определенное время суток может быть охарактеризован АКФ конкретного вида. Знание об этих закономерностях сетевого трафика должно учитываться при разработке новых способов обнаружения аномалий и атак для повышения их эффективности.

Разработанность темы

В литературе под обнаружением аномалий обычно понимается либо обнаружение специальных сигнатур (например, IP-адресов из черного списка), либо отклонений в последовательности значений некоторого параметра, выделенной из сетевого трафика [2]. Иногда используются данные протоколов SNMP и NetFlow (и их вариантов) [3].

Выделяются алгоритмы обнаружения отклонений, основанные на анализе суммарного объема трафика или отдельных его признаков. В работе [4] проводится обзор различных методов, в том числе метода главных компонент (PCA) применительно к объему трафика, подходы на основе вейвлетов применительно к сигналам, выделенным из трафика.

В работе [5] для анализа различных временных рядов, выделенных из сетевых потоков, применяется алгоритм на основе фильтра Калмана и двухшагового метода прогноза и коррекции. По отклонению значений, полученных на этапе коррекции, делается вывод о наличии аномалии в рассматриваемых данных. Размерность данных предварительно уменьшается путем применения метода главных компонент.

Басараб и др. [6] приводят обзор существующих подходов к обнаружению сетевых аномалий на основе методов мультифрактального анализа, так как сетевой трафик проявляет фрактальные свойства и может быть охарактеризован некоторым значением показателя Херста. При возникновении аномалии значения показателя Херста и фрактальной размерности могут отклоняться от ожидаемого.

В данной работе предлагается способ обнаружения аномалий на основе линейной фильтрации временного ряда, полученного из трафика и представляющего его интенсивность. Фильтр Винера, синтезированный для трафика в нормальном состоянии сети, позволяет вычислить минимальное значение среднеквадратической ошибки фильтрации. Значительное отклонение значения ошибки, полученной во время функционирования сети, может служить признаком аномалии.

Методология

Сетевой трафик можно рассматривать как аддитивную смесь x (t ) = 5 (t) + n (t),                                           (1)

где s(t) – процесс, представляющий ожидаемый трафик (количество пакетов в единицу времени); n(t) – процесс, представляющий флуктуации трафика в разные дни и недели (шум наблюдений).

Процесс s(t) не может иметь отрицательные значения, так как представляет по определению неотрицательную величину. Сложение с n(t) также не должно приводить к появлению отрицательных значений:

min s ( t ) + min n ( t ) > 0.                                (2)

Фильтр Винера является оптимальным по критерию минимума среднеквадратической ошибки:

s 2 ( t ) = E { ( ⁵ ( t ) - ⁵ ( t ) ) 2 } ,                                     (3)

где E{∙} – символ усреднения.

Для применения данного фильтра процессы s(t) и n(t) должны быть в широком смысле стационарными. В [7] представлены выражения для получения импульсной характеристики фильтра в непрерывном времени. При компьютерном моделировании разумно перейти к рассмотрению дискретного времени. В матричной форме импульсная характеристика фильтра Винера может быть получена как h = Bx-1 ■ bxs,                                        (4)

где h – вектор отсчетов импульсной характеристики фильтра; B _x – корреляционная матрица процесса x(t) ; b _xs – вектор отсчетов взаимной корреляционной функции (далее – ВКФ) процессов x(t) и s(t) [7].

С учетом (1) это выражение примет вид h = (Bs + Bsn + Bns + Bn )-1 ■(bs + bsn ),                        (5)

где B _s – корреляционная матрица процесса s(t) ; B _sn – матрица взаимной корреляции процессов s(t) и n(t) ; B _ns – матрица взаимной корреляции процессов n(t) и s(t) ; B _n – корреляционная матрица процесса n(t) ; b _s – вектор отсчетов AКФ процесса s(t) ; b _sn – вектор отсчетов ВКФ процессов s(t) и n(t) [7].

Значение среднеквадратической ошибки фильтрации (3) равно нулю только в том случае, если спектры процессов s(t) и n(t) в частотной области не пересекаются, что в реальных условиях практически недостижимо.

Минимальное значение ошибки может быть найдено как [8]

e min = b s [ 0 ] - b xs T ■ B x ^{- 1} ■ b xs .                            (6)

При этом нормированное минимальное значение ошибки (возможные значения которой лежат в интервале [0,1]) [8]

Среднеквадратическая ошибка фильтрации как критерий обнаружения аномалий ...

min

2 ,

^CT s

£2.

min

где s ² _s – дисперсия процесса, представляющего нормальный трафик.

Суть методики обнаружения аномалий сводится к следующему. Во время периода обучения (наблюдения трафика, характерного для нормального функционирования сети) выделяются локально-стационарные периоды, соответствующие основным сценариям ис- пользования сети, сохраняются их статистические характеристики для дальнейшей идентификации и выборочные АКФ (8), необходимые для синтеза фильтра. После анализа разброса значений для разных периодов, соответствующих одному и тому же сценарию, принимается некоторая модель процесса, представляющего шум наблюдений. Он может быть как коррелирован с ожидаемым трафиком, так и не коррелирован. В соответствие сценарию использования сети ставится фильтр с определенной импульсной характеристикой и минимальной среднеквадратической ошибкой:

N

B xy ^(т ^"^Я x ⁽ t ^{+ т ) -} E { x ^}M у ⁽ t ^{) -} E ^{ у ^} ) . N t = 0

Во время использования сети с определенной периодичностью происходит фильтрация трафика, наблюдаемого на текущем интервале (в текущем скользящем окне). По статистическим характеристикам текущего периода определяется наиболее вероятный сценарий использования: к трафику применяется фильтр, и для полученной оценки вычисляется среднеквадратическая ошибка фильтрации. Ее значение сравнивается с мини- мальным значением для данного сценария.

Процесс на выходе фильтра, или оценка, вообще говоря, является смещенной, поскольку в соответствии с (2) обладает ненулевым средним. Для получения несмещенной оценки перед применением фильтра из x(t) необходимо вычесть средние значения s(t) и n(t) . Для восстановления реального значения оценки эти значения необходимо прибавить после фильтрации.

Значительное отклонение ошибки фильтрации от предварительно вычисленного минимального значения может говорить о том, что в наблюдаемом трафике появился его новый аномальный источник. Для определения значимости отклонения необходимо выбрать некоторый статистический критерий принятия решения, например, t-тест Стьюдента.

В данной работе проводится моделирование такого случая и рассматривается один локально-стационарный период. В соответствии с условием (2) для моделирования s(t) используется случайный процесс с законом распределения Вейбулла с параметрами формы и масштаба, равными единице. Данный закон распределения характерен для трафика с долговременными зависимостями [9]. В качестве модели n(t) принимается случайный процесс Y = |X|, где X – не- коррелированный случайный процесс с нормальным законом распределения М (0, ст2) Предполагается, что процесс s(t) имеет АКФ вида sin(x)/x:

sin ( т / т ₀ ) ^{т / т} о    ,

B ( т ) = ст ²

где s ² – параметр дисперсии; t ₀ – параметр времени корреляции.

Для моделирования задаются значения параметров ст = 1 и т0 = 500. Предполагается, что взаимная корреляция между s(t) и n(t) отсутствует, тогда формулы (5) и (6) примут вид соответственно h=( Bs+Bn )-1 ■ bs;

e ™in = b s [ 0 ] ^- b s T ■ ( B s ⁺ B n ) ¹ ■ b s .

При моделировании учитываются первые 1000 отсчетов корреляционных функций (порядок фильтра = 1000). Нормированная среднеквадратическая ошибка в том случае, когда процесс s(t) имеет закон распределения Вейбулла, примет вид

P 2  _ ° min

° min =    2

⁷ S

w

² min

1 ^: rll 2 ^x T⁺ k

-Г ² | 1 + ¹ V k

,

где у 2 - дисперсия распределения Вейбулла; X - коэффициент масштаба распределения Вейбулла; k – коэффициент формы распределения Вейбулла; Г(∙) – гамма-функция.

Для моделирования случайного процесса с заданным законом распределения и автокорреляционной функцией используется методика, основанная на получении циркулянт-ной корреляционной матрицы и преобразовании Фурье [10].

Определяется нормированное минимальное значение среднеквадратической ошибки при различных значениях отношения сигнал/шум и реальное значение ошибки для случая, когда фильтр применяется к процессу (1). Затем производится моделирование случая, когда в трафике появляется аномальный процесс a(t) , то есть процесс на входе фильтра определяется как

X ( t ) = s ( t ) + n ( t ) + a ( t ) .

Рассматривается три случая: а) процесс a(t) имеет АКФ вида sin (x)/x (9); б) процесс a(t) имеет АКФ экспоненциального вида (14); в) процесс a(t) имеет АКФ треугольного вида (15).

i ( Iki)

B ( k ) = < 7 ² exp I -— I .                                (14)

I ^k о )

B (k ) =

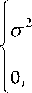
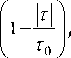
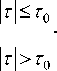
Процесс a(t) действует на всем периоде наблюдений. Определяется реальное значение нормированной среднеквадратической ошибки фильтрации при различных значениях отношения сигнал/шум (SNR). Параметр < 7 ² шума n(t) определяется из соотношения

₇ 2 = E { s ⁽ t ^{) 2} }

SNR , где E{∙2} – второй момент случайной величины; SNR – отношение сигнал/шум.

Результаты

Моделирование производилось в специально разработанной программе на языке Python. Рассматривались следующие значения отношения сигнал/шум: 1/100, 1/10, 1/2, 1, 2, 10, 100. Для каждого значения был синтезирован фильтр и проведено по 10 экспериментов, в каждом из которых генерировались случайные последовательности длиной 100 000 отсчетов с заданными законами распределения и АКФ, к которым применялся фильтр.

Среднеквадратическая ошибка фильтрации как критерий обнаружения аномалий ...

Сначала рассматривался процесс x(t) (1) без аномалии (Рисунок 1). Пунктирной линией представлены рассчитанные по формуле (12) нормированные минимальные значения среднеквадратической ошибки. Средние за 10 экспериментов значения среднеквадратической ошибки фильтрации представлены сплошной линией, вертикальными чертами отмечены значения стандартного отклонения для каждого значения отношения сигнал/шум.

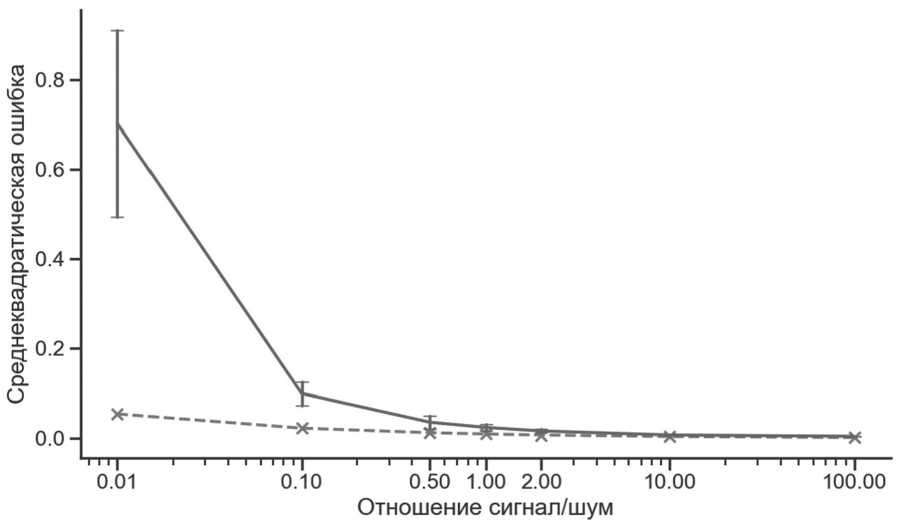
Рисунок 1. Среднеквадратическая ошибка фильтрации трафика без аномалии Источник: составлено авторами.

По графику видно, что в случаях, когда шум преобладает, реальное значение ошибки сильно отклоняется от минимального. При уменьшении мощности шума реальное значение ошибки приближается к минимальному.

На Рисунке 2 представлен график для процесса x’(t) (13) с различными видами аномалий, где дополнительно было отмечено значение ошибки, равной 1.

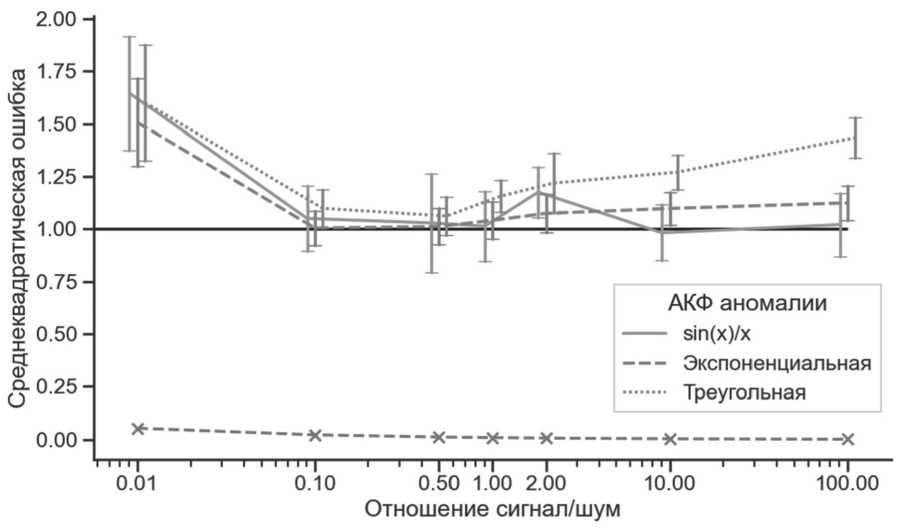
Рисунок 2. Среднеквадратическая ошибка фильтрации трафика с аномалией

Источник: составлено авторами.

Если на вход фильтра поступает процесс x(t) без аномалии, то значение нормированной ошибки должно лежать в интервале [0,1] [8]. По графику видно, что почти во всех случаях наличие аномалии в поступающем на вход фильтра трафике приводит к увеличению значения ошибки и превышению верхней границы, равной 1.

Заключение

Рассмотрен способ обнаружения аномалий в сетевом трафике на основе фильтрации наблюдаемого трафика. Проведено компьютерное моделирование с использованием сгенерированных реализаций случайного процесса x(t) , имеющих заданную АКФ. При добавлении к процессу, представляющему нормальный трафик, процесса, представляющего погрешность изменений (шум), для которых был синтезирован фильтр, значение среднеквадратической ошибки фильтрации не сильно отклоняется от ожидаемого минимального значения. При добавлении к поступающему на вход фильтра трафику аномального процесса a(t) значение среднеквадратической ошибки фильтрации значительно возрастает и выходит за интервал [0,1], в котором должны лежать все значения нормированной среднеквадратической ошибки, если на вход фильтра поступает только ожидаемый процесс и шум. Это является признаком наличия аномалии в обрабатываемом трафике.

Данный эксперимент соответствует рассмотрению одного локально-стационарного периода в сетевом трафике, статистические характеристики которого могут, например, представлять сценарий использования сети в рабочее время. Результаты моделирования позволяют говорить о том, что отклонение значения среднеквадратической ошибки фильтрации может указывать на наличие аномального источника трафика в сети, то есть использоваться в качестве критерия обнаружения аномалии.

В дальнейшем следует рассмотреть АКФ реального самоподобного трафика, исследовать влияние на статистические свойства трафика аномалий, действующих не на всем периоде наблюдений, а лишь на некоторой его части, а также разработать методику оценки флуктуаций трафика в разные дни и недели (шума наблюдений) на основе наблюдения нормального трафика.