Средняя доля недообслуживания заявок в системах массового обслуживания

Вводится характеристика СМО – средняя доля не-дообслуженных заявок. Показано, что указанная характеристика определяется разностью второго и первого начальных моментов числа заявок, поступающих в течение каждого интервала времени обслуживания.

Среднее значение времени дообслуживания заявок является одной из характеристик систем массового обслуживания (СМО). Она характеризует среднее время, необходимое для завершения обслуживания ранее выбранной заявки [1].Это время учитывает,что на момент поступления очередной заявки в системе может не оказаться ни одной заявки, то есть предыдущая заявка была обслужена полностью и время ее дообслуживания равно нулю. Вместе с тем,имеется еще одна не менее важная ха-рактеристика,которой,нанашвзгляд,втеорииСМО уделяется недостаточное внимание.Это – средняя доля недообслуживания заявок. Она характеризуется средним числом недообслуженных заявок,за время обслуживания очередной заявки.При этом может оказаться, что в течение указанного времени в систему не поступает ни одной заявки и число не-дообслуженных заявок будет равно нулю.

В [2] показано, что основное влияние на процесс формирования очередей в СМО оказывают математическое ожидание E (n) и второй начальный момент E ( n ) числа заявок, приходящихся на одну обработанную заявку.

E (n²) - E (n) q =--------------- ,               ⁽¹⁾

2 (1 - E (n))

где q – средняя длина очереди в одноприборной СМО. При анализе СМО поток заявок обычно характеризуется плотностями вероятностей распределения интервалов времени между соседними заявками W( 9 ) и распределения интервалов времени обработки указанных заявок W( т ) . В данной работе мы попытаемся установить зависимости между указанными временными характеристиками и средней долей недообслуженных заявок в СМО.

Анализ проведем с использованием функций распределения вероятностей интервалов между соседними заявками для потоков различного порядка, получаемых путем резреживания исходного потока.

На рис. 1. показана временная диаграмма исходного стационарного рекуррентного потока заявок, для которого случайная величина ϑ1 интервалов между соседними заявками распределена по закону, имеющему плотность вероятностей W( 9 ) и функцию распределения вероятностей

τ

F(t) = P(^< т) =J W(^)d^ . (2) 0

На том же рис. 1 показаны потоки заявок более высоких порядков, для которых

Fn (т ) = P (9 n <  т ) ,

n где ^n = X ^k . Функции распределения веро-„ k=1

ятностей для потоков n -го порядка назовем образующими функциями.

Поток, соответствующий образующей функции n -го порядка, получается путем удаления из исходного потока подряд ( n - 1 ) заявок, с сохранением каждой n -ой заявки. Следовательно, функция распределения вероятностей интервалов для исходного потока имеет первый порядок Fy ( т ) = F ( т ), поскольку из него не удаляется ни одной заявки.

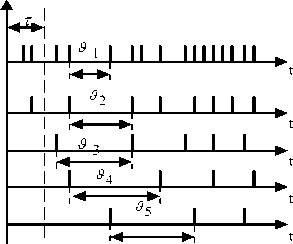
Рис. 1. Разреживание потока

Интервалы времени между моментами поступления двух соседних заявок для потока n -го порядка получаются в результате суммирования независимых случайных величин, распределенных по закону исходного потока. Следовательно, математическое ожидание E(Эп ) интервалов между моментами времени поступления соседних заявок и соответствующая дисперсия D( ^ n) определяются соотношениями:

E(Pn) = n E(S 1);

D(Sn) = n D(P 1).

Коэффициент вариации интервалов времени для потока n-го порядка v2(9n)=

D ( 9 n )

[ E ( 9 n ) ] ²

v2(9 i)

n

уменьшается по сравнению с исходным потоком, с увеличением порядка n , что и следовало ожидать.

Рассмотрим распределение числа событий, попадающих на интервал τ для каждого из потоков, представленных на рис. 1. Обозначим через Pi ( п , т ) вероятность поступления на интервале τ ровно i событий потока n -го порядка. Для реализации потока, показанной на рис. 1, следует, что в течение интервала времени τ поступили два события исходного потока, одно событие – потока второго порядка. Для потоков третьего, четвертого и пятого порядков не поступило ни одного события.

Вероятность отсутствия событий на интервале τ для потока n -го порядка равна вероятности того, что интервал между соседними событиями в этом потоке превышает τ :

P 0 (п, т ) = P( ^ n >  т ) = 1 - Fn ( t ). (6)

Событие, состоящее в том, что на интервале τ возникнет ровно i заявок исходного потока, произойдет лишь при одновременном выполнении двух условий: (S i <  т ) и (S i _{+ 1} >  т ) . Следовательно, вероятности указанных событий

P (1,т) = P (Pi < т) - P (Pi+1 > т) =

= Fi (т) [1 - Fi+1(т)] .

После соответствующих преобразований, получим

Pi' ^{(1, т} ) = Fi ^{( т} ) - Fi + 1^{( т} )• i = 0; 1; 2 ...

Здесь необходимо учесть, что

Fq(t) = P(0 < т) = 1.

Очевидно, что (7) соответствует (6) при i = 0 , n = 1 и обобщает закон Пуассона на неэкспоненциальные потоки.

Учитывая, что представляет интерес лишь распределение вероятностей числа событий для исходного потока, Pi (1,т) будем обозначать через Pi ( т ) , опуская 1.

Определим значение суммы вероятностей поступления от 0 до n заявок на интервале τ :

nnn

X Pi- (Т) = X Fi (Т) — X Fi+1(т) = i=0        i=0

nn

= Fo(t) + X Fi(Т) — X Fj(Т) = i=1

= Fo(t) + X Fi(т) — X Fj(Т) — Fn+1(т) = i=1

= 1 — Fn+1(T).

Учитывая ^lim F i + 1 ^{( t} ) = 0, получим да              n ^ro

У Pi ( т ) = 1 . Найдем математическое ожидание i = 0

Е[п( т )] числа событий исходного потока, возникающих на постоянном интервале времени τ :

го               го

Е[п(т)] = Е i • Pi(т) = Е i • Fi"(т)-i=0

гого

• - Е i • F i- +1 ^{( т} ) = ^F i ^{( т} ) ⁺ Е i • Fi" ^{( т} ) -

• i=1

гого

• — е ⁽ i +1) • Fi +1^{( т} ) + Е i • Fi" +1^{( т} ) =

i=1

гого

• = F1(T) + Е i • Fi (т) - Е i • Fi (т) + i=2

гого

• + Е Fi ( т ) = Е F- ( r ).

i = 2

Получили удивительный результат:

E[n(T)] = У Fi (т).

i = 1

Определим второй начальный момент

2

E[n (т )] числа событий исходного потока, возникающих на постоянном интервале времени τ :

E[n2 (т)] = S i2 • Pi(t) = S i2 ■ Fi(t)-i=0            i=0

да

• — S i² • Fi ₊ i( t ).

i = 0

После преобразований получим

E[n2 (t)] = 2 S (i -1) • Fi (т) + S Fi (t). (9) i=0

С учетом (8), получим окончательно

E[n2(T)] - E[n(T)]

--------------------= S (i -1) Ft (t). (10) 2

Обозначив через Е [ Ап ( т )] выражение в левой части (10), получим

E[An(T)] = X (i -1) Fi (т).

i=1

В дальнейшем будет показано, что именно эта величина в СМО характеризует среднее число не-дообслуженных заявок за постоянное время τ .

Рассмотрим, представленный на рис. 2а стационарный поток заявок на обслуживание в СМО. Допустим, что все заявки обслуживаются с постоянным временем τ . Распределим указанные интервалы обслуживания на оси времени, как это показано на рис. 2., причем заявки, после которых начинается отсчет интервалов времени τ , считаются не принадлежащим указанным интервалам. Началом каждого очередного интервала τ считается момент появления заявки, которая непосредственно следует за окончанием предыдущего интервала времени обработки. Эту операцию следует повторить начиная отсчет времени обработки от каждой заявки.

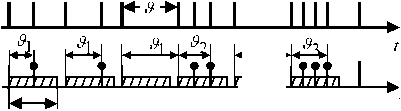
а

б

ϑ 1

пша

t

Рис. 2. Стационарный поток заявок

Из рис. 2б следует, что в течение постоянных интерваловобработки поступаетразличное число заявок i. Например, в течение первого и второго интервалов поступило по одной заявке, в течение последнего интервала – три заявки. В течение третьего и четвертого интервалов не поступило ни одной заявки. Из рис. 2б также следует, что случайные величины 9i получаются каждый раз в результате суммирования i интервалов д между заявками исходного потока. При этом, всегда выполняется условие ^i < т . Вероятность выполнения такого условия - P(ty < т), как было показано в (3), равна Fi- (т). Каждому событию ϑi ≤ τ соответствует появление на интервале обработки i заявок. Поскольку в течение интервала времени всегда полностью обрабатывается одна заявка, то недообслуженными будут оставаться каждый раз (i -1) заявок. Из указанных рассуждений следует, что среднее число недообслужен-ных заявок, приходящихся на одну обслуженную заявку, определяется соотношением

∞

X (i -1) Fi (т), i=1

что полностью соответствует (10)-(11).

Таким образом, мы показали что выражения (10)-(1 1) определяют среднее число (долю) не-дообслуженных заявок, приходящееся на постоянное время τ обслуживания одной заявки. Именно указанной величине пропорциональна средняя длина очереди в СМО при любом законе распределения интервалов времени между соседними заявками.

Если интервалы времени обработки τ не постоянны и имеют плотность вероятностей W ( т ) , то

да

E (n) = J E[n(т)] -W (т )dt0

да

E(n ) = J E[n2 (т)] - W(т)dt =0

да

= J E2 [п(т)] - W(т)dt +

да                                  2

+ J D[n(т)] -W(т)dt = [E(n)] + D(n), 0

где D [ n ( T )] дисперсия числа заявок поступающих в течение постоянного интервала обслуживания τ .

Средняя доля недообслуженных заявок E ( ^ n ) определится соотношением

∞

E(Nn) = J E [Ап(т)]W(t)dtt =

∞∞

= S (i -1) J Fi (t )W (t )d T .

i=1       0

Если, например, каждое вновь возникающее событие обрабатывается с вероятностью P_k в течение времени т к ( к = 1; 2 ... m ) , то есть

W ( т ) = X Pk • 5 ( т к - т ) , то к = 1

m

E ( Nn ) = X E [ ^п ( т ) ] Pk • 3 ( тк - т ) = к =1

mm

= X E [ Ап( т ) ] • Pk = X Pk х          (13)

к =1                  к =1

m х X (i — 1) • Fi (тк) .

к =1

Соотношение (13) устанавливает зависимость характеристики СМО - E [ Д п ( т ) ] от значений семейства образующих функции F" (т) .

Получение аналитических выражений для функции распределение i -го порядка из функции F 1 ( t ) распределения вероятностей исходного потока в общем виде не всегда возможно. Однако, для потоков, интервалы между соседними заявками в которые подчиняются Г -распределе-нию, такие зависимости устанавливаются весьма просто. Допустим, что функция распределения интервалов между соседними заявками в исходном потоке подчиняется Г -распределению

х ( т ) . ,             х ( т )

г i n - 1   -x            ( i+ 1) П - 1   -х>

∫x e dx ∫x          e dx

Hi п )              r [ ( i + 1) п ]

Указанное соотношение является интегральным обобщением закона Пуассона на потоки с Г -распределением интервалов межу соседними заявками.

Поскольку экспоненциальное распределение интервалов есть частичный случай Г -распределе-ния при η = 1 , следует ожидать, что в результате такой подстановки мы должны прийти к формуле закона Пуассона.

В указанном частном случае

х(Т) i 1     У i 1     x

∫ x e dx

Pi (1, т ) = -°

Г( / )

х (т ) . _—

∫ x e dx

0 ___________

Г( . +1)

здесь η = 1 .

Известно, что max 1 ma⋅x  m-1 ax

∫ xedx =⋅ xe -∫ x ⋅ e dx ,

a с учетом этого соотношения

Pi (1, т )

^x ( ^T ) X ^{- 1} e ^{- x} dx ₊ x ( t ) i e - ^{x ( T} ) J       Г( 1 )    ⁺    r (i + 1)

-

х (т)     ,

∫ x η    e^x dx

F (т ) = -0

Г (П)

^x ( ^T ) i x^{(i - 1)} e ^{- x} dx = x ( t ) i e - ^{x ( T} ) j       r (i + 1)     = i !

пт        1

где x ( т ) =-------; п = т;-----

E ⁽ ^ 1)        v 2( 5 1)

обратная квадрату коэффициента вариации ин-

–

величина,

тервалов между заявками в исходном потоке.

Поскольку случайные интервалы ϑ_i между соседними заявками в потоке i -го порядка получаются в результате последовательного суммирования i интервалов ϑ ₁ исходного потока, функция распределения интервалов между соседними заявками, в потоке i -го порядка, также будет подчиняться Г -распределению. В соответствии с (4)(5) указанная функция имеет вид:

х(т) •     , г   i П-1 - Xj

∫ xedx

τ

i

Fi (т ) =

r ( i П )

Подставляя значения из (15) в (7) для Г -рас-пределения интервалов, получим

E W

i

τ e E(^1)

что и следовало ожидать. Получили закон Пуассона для исходного потока

Pi (1, T ) =

E [ n( T ) ] i e~E ^{[ n ( T ) ]} i !

где

E ^{[ n ( T ) ]} = D ^[ n ^{( T ) ]} = —^T— .       (18)

E ⁽^ 1)

Если интервалы времени обслуживания не постоянны, а имеют плотность вероятностей W ( т ) , то с учетом (12) и (18) для пуассоновского потока получим:

E (т )

= ρ

E ( ^ 1)

2 E ( т )

_ E (^1) _

E (n) =

2х

• 2,    E ^{( т} )

E ⁽ n ) = —---=

E 2(^1)

2

(1 + v2) =

(1 + V2) ,

2    D(t )

где vT =-----^ - коэффициент вариации интер- валов времени обработки. Путем подстановки в (1), получим формулу Хинчина-Поллячека для экспоненциального распределения интервалов между заявками

2 л 2Л

Р (1 ^{+ v}t ) q =------------- ,

2(1 - Р )

Заключение

В соответствии с (1), средняя доля недо-обслуженных заявок определяется разностью второго и первого начальных моментов случайной величины числа заявок, поступающих в течение случайных интервалов времени обслуживания заявок. Именно указанные параметры целесообразно определять при экспериментальном исследовании СМО.