Stability analysis of equilibrium points of newcastle disease model of village chicken in the presence of wild birds reservoir
Автор: Furaha Michael Chuma, Gasper Godson Mwanga
Журнал: International Journal of Mathematical Sciences and Computing @ijmsc
Статья в выпуске: 2 vol.5, 2019 года.
Бесплатный доступ
Newcastle is a viral disease of chicken and other avian species. In this paper, the stability analysis of the disease free and endemic equilibrium points of the Newcastle disease model of the village chicken in the absence of any control are studied. The Hurwitz matrix criterion is applied to study the stability of the Newcastle disease free equilibrium point,Q0. The result shows that the disease free equilibrium point is locally asymptotically stable iff the principle leading minors of the Hurwitz Matrix, (for n∈ℝ+) are all positive. Using the Castillo Chavez Theorem we showed that, the disease free equilibrium point is globally asymptotically when R0-1. Furthermore, using the logarithmic function and the LaSalle’s Theorem, the endemic equilibrium point is found globally asymptotically stable for R0-1. Finally the numerical simulations confirm the existence and stability of the equilibrium points of the model. This reveals that, proper interventions are needed so as to decrease the frequently occurrence of the Newcastle disease in the village chicken population.
Stability analysis, Equilibrium points, Newcastle disease, Village chicken
Короткий адрес: https://sciup.org/15016689
IDR: 15016689 | DOI: 10.5815/ijmsc.2019.02.01
Текст научной статьи Stability analysis of equilibrium points of newcastle disease model of village chicken in the presence of wild birds reservoir
Published Online April 2019 in MECS DOI: 10.5815/ijmsc.2019.02.01
(for n > 0) in a geometrical space [4, 11]. A steady state solution, X ( t ), is an equilibrium point of a dynamical system X' = M ( X , t ), X e K n if satisfies the condition M( X *,0) = 0, V t > 0 [11, 19, 21]. The solution X ( t ) of a dynamical system is stable if, for any arbitrarily small 8 > 0 , there exists 5 > 0 such that, for any trajectory X ( t ) for which || X (0) - X *(0)|| < 5 , then the inequality || X (0) - X *(0)|| < 8 is satisfied V t > 0 [19]. It is also stable iff all initial trajectories in an open set X e K n move towards X ( t ) and remain near it V t > 0 and is unstable if moves away from X ( t ) [21, 24, 25].
The steady state solution is referred as a disease free if the population is free from the disease whilst referred as the endemic if the disease persists in the population [16]. In this paper we study the existence and stability of both disease free equilibrium point (DFEP) and the endemic equilibrium point (EEP) of the Newcastle disease (ND) model developed by [6]. We apply a Hurwitz Matrix criterion to study the local stability of the disease free equilibrium point and the Castillo Chavez theorem [5] to study the global stability of the disease free equilibrium point. In addition, we apply the La Salle’s invariant principle and the Lyapunov method to study the stability of the endemic equilibrium point. Lastly, we use simulations to verify the analytical solutions of the ND model with environment and wild birds reservoirs. The motivation of this paper is to understand the existence and stability of the equilibrium points of the Newcastle disease model when wild birds are considered as the reservoir of the Newcastle disease virus. However, no study till yet in the field have considered the wild birds and environment as the secondary sources of ND.
-
2. Related Works
Several stability analysis methods have been applied by different scholars when analyzing their epidemiological models [2, 16, 17, 18, 19, 21].
-
[12] used the trace and determinant method to study the local stability of the disease free equilibrium point of their models. In this method, the signs of trace and determinant of the variational Jacobian matrix decides the local stability of the disease free equilibrium point. [2] used the Lyapunov function to prove the global stability of the disease free equilibrium point of Dengue disease infection Model. [19] used a linearizion method to study the behavior of the disease free equilibrium point of a deterministic Epidemiological Model with Pseudorecovery. Additionally, [19] used a Lyapunov function method to study the stability of the endemic equilibrium point of his model. Moreover, [2, 17, 21] used Metzler matrix theorem to study local stability of the disease free equilibrium point of their models. Further, a Lyapunov method and the La Salle’s theorem are used by [21] to study the stability of the endemic equilibrium point of Malaria model. [16] used the Center Manifold theorem to study the global stability of the endemic equilibrium point of the Malaria model. In our model, the Hurwitz matrix criterion is applied to study the stability of the Newcastle disease free equilibrium point,
-
3. Model Formulation
-
3.1. Equations of the Model
In formulation of the model it is assumed that, the birth rate and death rate of the village chicken are the same. These populations are recruited at a constant birth дN (t) and д N^(t) with Nc (t) and Nw (t) as the total population of the village chicken and wild birds respectively. According to [6], the wild birds population N (t) is partitioned into susceptible S (t), exposed E (t) , the mildly infected wild birds I (t) and severely infected I (t) . The mild infected wild birds are not capable of transmitting the ND to other birds. The Village chicken population is partitioned into susceptible S (t) , exposed E (t) and the severely infected I (t) . The contaminated environment is denoted by H(t) The model assumed that the transmission of the NDV among the hosts is primarily through direct contact between the infected and susceptible chicken is the primary route for NDV while the contact of susceptible chicken with either contaminated environment or reservoir wild birds is the secondary route of the virus transmissions [7, 13]. Village chicken spread the ND virus after developing the clinical signs within the incubation period of two to fifteen days [1, 20, 23]. Furthermore, we assumed that the severely infected village chicken, severely infected wild birds, and the mildly infected wild birds all shed NDV into the environment at the rate α and α respectively. Other parameter of the model system
(1) Are described as in the table below;
Table 1. Parameters used for the ND Model System (1)
|
Parameter a b φ |
Description Contact rate between the susceptible and mildly infected wild birds Contact rate between mildly infected wild birds and susceptible Chicken Contact rate between severely infected and susceptible wild birds Contact rate between severely infected and the susceptible chicken |
|
ψ k d ρ |
Contact rate between severely infected and susceptible chicken Half saturated constant of NDV in the environment Probability of chicken and wild birds to get infections from the environment Probability of the exposed wild bird to become severely infected |
|
α c |
Shading rate of NDV from severely infected village chicken to the environment |
|
α w µ |
Shading rate of NDV from mild and severe infected wild birds to the environment Recruitment rate and Natural mortality death rate of the hosts |
|
µ v δ w |
Clearance rate of the NDV from the environment Disease induced death rate in wild birds population |
|
δ c γ |
Disease induced death rate in the village chicken population Progression rate of ND for village chicken and wild birds |
From the model flow descriptions found in [13], we have the following system of ODEs
^ = pNc (i) - (ti-^ + b^ + ^7^ + m) SeW ^ = (^ + 6^ + S) S^ - ^ + ^(«) ^^ЕДО-^-ИШЦ
^ = pN. (,) _ (№M0 + ^ + „) S4t)
^ = (^t'^1 + S) S„W " (7 + iWt)
^ = (l-phEw(t)-/1Jr(t)
^y =
aJe^
+ a. (/„(/) + Zr(t)) -
n.H(t')
with the initial conditions;
S
c
(0)
>
0,
Ec
(0)
>
0,
I
c
(0)
>
0,
S
w
(0)
>
0
,
E
(0)
>
0,
I
w
(0)
>
0,
I
r
(0)
>
0
,
H(0) > 0, N(t) = Sc(t) + Ec(t) + Ic(t) and N*(t) = S(t) + E(t) + I*(t) + Ir (t)
4.1.
t
he
b
asic
r
eproduction
n
umber
,
R
As shown in [13], the Basic Reproduction Number of the model system (1) is;
- , ^f^
a(p-1)7 , ^„«„7(<$w+^-/>($„)\
\ h+/i)(^w + M) (7 + Д)Д
* (7 + w(^W+^)M/*v /
/(у
__££7__
д(р- 1)7
_
dN
„n„7
(i.+li + p6.Y
\2 . *
'VX (7 + /C(^+/0
(7 + ^)m
Ц-f + MU^nJ
where
Y _
*1
dN^ ac
(7 + /j)(<$, + p) к (7+р)(<$с + д)/1„ д _ 4 dN„у2 ac / bNe (p - 1) dNcOi», (6W + p + рб^
K (7 +
m) <& +
p) Щ) \NM
(7 +
P)P K ("V + P) + p)Ppv
4.2. Equilibrium Points of the Model System
Proposition 4.1
The model system has two equilibrium points, disease free equilibrium point
Q0
=
{
N
c
,0,0,
Nw
,0,0,0}
and the endemic equilibrium point
Q*
=
{
S
*
,
E
*
,
I
*
,
S
^
,
E
*
,I
*
,I
r
,
H
}
.
where
/• = _'^e;, e*c
= A5L,
s:
= ^L
Oc-r P p-r“f Ре + P
Substituting
S
into
E
and
E
into
I
we get
6
r = 1 UPcN*
By considering the force of infections in chicken,
I
is obtained by solving the equation
Where Also in the wild birds population we have the following steady states; Where 3W = (^WW + ^^y) and
7? t =
^N-.h
^+149-+^
From equation
(3)
to
(13)
, the solution
β
=
β
=
0
gives the disease free equilibrium points while
β
≠
0and
β
≠
0
gives the endemic equilibrium point of the model in the system (1).
4.3. Local stability of the Disease Free Equilibrium Point
The stability analysis of the disease free equilibrium point (
Q
0) of the model system (1) is examined by the Hurwitz Matrix criterion [22]. The Jacobian matrix
J
(q
0)is found by differentiating each equation of the model system
w
.
r
.
t
its state variables at
Q
0 . Thus, the Jacobian matrix of the model system at
Q
0 is then given by
1-t*
0
-V
0
0
0
-b^
-d^
0
-ji-7
*
0
0
0
d^
0
7
— <$c — /4
0
0
0
0
0
w=
0
0
0
—[1
0
-p
—Й
-j^
0
n
0
0
-ft
- 7
ti
d!^
0
0
0
0
P7
-&W — M
0
0
0
0
0
0
(i - ph
0
0
<0
0
de
0
0
№»
аш
-1^ ;
From matrix (14) the first two roots
of
J
(
Q
0
) are
given by (
-
д
—
2
)
=
0 and (
-
д
-
2
)
=
0 . Then the
reduced
(6
x
6)
matrix become
with
n
=
bN-
,
5
=
dN
c.
and
t
=
dNw
Nw
k k
Then characteristic polynomial for the matrix is defined as
G
(A) = A6 + Bi As + B2A4 + B3A3 + B4A2 + B5A + a6
The corresponding Hurwitz matrix is then given by
'bv
B3 Bs 0
0 0
1 B^ B3 Bs о0 , 0 Bi в3 в3 о0 Gif = 0 1 B4 Bl Ba0 0 0 Bi Bt Ba0
у 0 0
\ B3 Bi Ba j
where,
Вх = Pv
+ 3/1 +
ф
4-
8С
4- 7
В,
= 7
р t + pv
7 + 3 д»
Р — Pv Ф
+ До
8С + ар + и8п,
4- 2 7 д —
уф — уф —
7 / + 7 <5С + 3 д2 —
Зфр + 2бср — ф6с
Вл = Р»У pt + y2pt
+ 27
ppt
4-
у pt8c + pvap
4-
p«a8w + 2p«y p — р„уф — реУФ — Ре
7
t + p„
7
8C
4- 3
pe p2
- 3
pv p ф
+ 2
p„ p 8C - р„ф8с + у ap
4-
ay 6W
4- 3
ap2 + 3ap 8W
4-
ap 8C + a8w 8C — y2t
4- 7
p2
— 2 7
рф—у рф
— 27
pt
+ 7
p8c + y фф — уф8с —
7 sac — 7
t8c
4-
p3
— 3
р2ф
4-
р28с — 2рф8с
Вл = р»у2р1
4-
2р„у ppt
4-
pvypt6c
— 73np —
y2pnp
4-
y2ppt — у2фpt — y2psaw
4-
y2p t8c+y p2pt+y p pt8c+Pt,
7
ap
4-
pv ay 8W
4-3
pe ap2
4-3
p„ap8W
4-дс
ap 8C
4-
Pv a8w 8C — pey2t+pey p2 —2pvy рф—рг,у рф—2 pt, у pt+pry p8c+pvy фф—fl,, у ф8с —
/^,7 td'c4-
pep3
— 3
fit,р2ф
4-
рг,p28c — 2pvрф8с + 2у ap2 — ay рф +2ay p6W
4-
ay p8C — ay ф6W
4-
ay 8W 8C
4- 3
up3
4- 3
ap28W
4- 2
ap28c + 2ap 6W 8C
4- 7Sr 4-
y2p r — y2p t
4-
у2ф t — y2t8c —
7
р2ф — у p2t
4- 7
рфф — у рф8с — у psac — ур t8c
4-
у фзас — р3ф — р2ф8с
Вц
= 2
р„ ар 8W 8С
4-
у2Ф р
saw 4-
у р Ф sa<, — pv у2р пр
4-
рт у2р pt—pe у2 ф pt+pv у2р t8c
4-
pt,
7
р2рt — p-t,
7
ар
^4-2
р„
7
ар8W + ргу ар8С — р„у аф
<$„ 4-
pv
7
и^«8С + рюу рФФ — р„ у рф8с—реУ р t8с—у2р stnc—y up sac—y asac 8W
—2
y2p p saw—y p
so#,
8w—ay p ф
d‘w4-
ay p 8e, 8C-Vpt,ypp t8c
4- 3
p„ up3 — px, рлф
4-
pB y3n
4- 73заш 4-
ay p3
4-
ap38w
4-
ap38c
4-
ap4 —
72sqw
8ь
— 7
p2saw + ay3np2 — ay3np — ay р2ф
4-
ay p28w
4-
ay p28c
4- 3 /^
ap28w
42
pv ap26c — pv р2ф8с — улр заш — pv y3np
4-
pv y2p n — pT y2p t
4-
ре тФ I
~ До 72^c + 2
pe
7
ap2 — pt,
7
р2ф — pv у p2t
4-
y2stac
4-
ap28w 8C
B6 = pt, ap28w 8C — y3p28taw
4-
y3p staw
— 7
ap2sac
4-
pT y3arp2 - pv улагр —
/a,
7
ар2ф
4-
Pv
7
ap28„
4-
pu
7
ap28c
— 7
ap sate 8W — Pv У ap ф 8W
4-
pT
7
ap 8W 8C
4-
y2p ф p заш
4-
pT up1
4-
Pt, ap38w-Vpeap35c+Pv
7
up3—aw y2p2s—aw
7
p3s—aw y2p s8w—am
7
р2н8ш+у3ар28ап, — y3apsalw
The disease free equilibrium point is locally asymptotically stable iff the principal leading minors of
G
are all positive for
n
= 1, 2,..., 6.
Thus
В,
B;t
S5
о
ag4 =
1
Вц
Вд
^
о
Bi
Вд
Вд
0
1
Ва
Вд
= B,B2 (B3B4 —
B2B4 + Вд^ + Вд (В2 — Вд)
— Вд ^ВдВд — В2В5 + в^в^ + В;
Bi Вд Вд
AG3 =
1
В2 Вд
= ВдВ^Вд — В^Вд — Вд + В1Вд.
0 Bi
Вд
Bi
Вд
Вд
0
о
О
1
в2
Вд
Ви
п
О
^Gfl =
О
Вт
Вд
Вд
О
о
о
1
в.
Вд
в»
О
О
0
Bl
Вд
Вт,
О
О
О
1
В2
Вд
Bti
= ВхВ^ВдВдВ^Вб
- В-’В* + В^ -
В6В»
+ 2В6В,В4В2 -
В24В»В6В& - ЗВ^ВдВдВд + 2В2В2ВаВ2 - ВдВ'^ВдВб + ВдВдВ^ + ВзВ2В6В? - ВбВхВ'^В! - BiBxB^B^.
t
he disease free equilibrium point
(
Q
0 )
of a model system
(1)
is
LAS
if
ДСЬ ДСз, .... ДСб > 0. For ДС1 > 0 we have
ц„
+ 3 p 4-
6C
+ 7 4-
ф>
0, ДСз > 0 if В|В.2>В3. AG3>0if
В1В2ВЛА-В1В5> B2B4A-B?V
Also ДС4, ДС5 and ДС6 are grater than zero when
B\B2B3B4A- BxB2B^ + ВлВ2 + BiB2B4 + B^ > B1B2B4 + B2 + B^B4 + BtBлВ4; В^В^ВдВ^В^
4-
В2 B2B3B6 + B4B3B4B^
4-
BtB^ + ВхВ2В^В^ + В2 > B4B^B‘2B^
4*
В\В2В2
4*
В\В4В3
4*
В^В^
4* В,В3В^ ^ and
В\В2ВлВхВ3Вц
4-
В^В^
4*
2B6BiB4B^
4-
2В2В2В-3В2
4-
В4ВЛВ2В2
4-
BAB2BtiB3
4-
В2 В2 > ЩВ'2
4-
В^В^В6В5
4-
АВ^ВхВ3В3
4~
В4В3В3В^ — В^В\ В2 В^
4~
В2В\В^В2
respectively.
We therefore establish a theorem;
Theorem 4.1
G
(
X
)
is stable iff the leading principal minors of
Gn
(Forall
n
e
®
+
)
are all positive and thus the disease free equilibrium point is
LAS
.
4.4. Global stability of the Disease Free Equilibrium Point
The global stability of the disease free equilibrium point of the ND model is done by the theorem as described by [5, 15, 16]. To apply the theorem, we write the model system (1) as; d4-F^ ^ = G(X,n,GW) = 0
Where
X
is the number of susceptible populations and
I
is the number of the infected populations whilst the disease free equilibrium point is given by
Q0
=
{
X
*, 0}
. For the system (18) to be
G
.
A.S
,
two conditions must be fulfilled;
I.
II.
d
X
*
=
F
(
X
0) ,
X
is globally asymptotically stable
G
.
A
.
S
,
dt
,
G(X, I) = BI - (G(X, I), (G(X, I) > 0for(X, I) eQ where Q is the invariant region and B = DG (X;0) is an M -matrix with non-negative off diagonal elements. If the system (18) satisfies condition I and II below then the theorem below holds:
Theorem 4.2.
A disease free equilibrium point (
Q
0) of a model described in system (1) is globally asymptotically stable
G
.
A
.
S
if
R
o<
1
.
Proof;
We need to show that condition
I
and
II
holds when
RQ
<
1. From the model system (1); the set of non-infectious classes is given by
X
=
(
Sc
,
S
)
e
К
2
and for the infectious classes is given by
I
=
(
Ec
,
I c
,
E
w,
I
w,
Ir
,
H
)
e
К
6
. The model system (1) is then transferred into the form of the system (18) as follows
with
Q0
=
{
N
,0,0,
Nw
,0,0,0}
. The system (19) is linear with the solutions
Sc
(
t
)
=
Nc
+
(
Sc
(0)
-
Nc
)
e ^
‘
and
Sw
(
t
) =
Nw
+ (
Sw
(0) -
Nw
)
e-^
. It is obvious that
Sc
(
t
)
^
Nc
,
S
w
(
t
) ^
N
w
as
t
^ да
depending on initial conditions. Thus,
Q
0 is globally asymptotically stable and therefore condition I holds. Considering the condition number II we have;
We need to show that, G (X, I) = BI - G (X, I), G (X, 0) > 0 for (X, I) e Q
The Jacobian matrix of equation (20) at
Q
0
produces an M-matrix
B
as follows;
f
rom the matrix
(21)
, a matrix
B
comprises with all negative diagonal entries and all non-negative off-diagonal entries. Since
N
c
(
t
)
=
S
c
(
t
)
+
E
c
(t
)
+
I
c
(
t
) and
N
w
(
t
)
=
S
w
(
t
)
+
E
w
(
t
)
+
I
w
(
t
)
+
I
r
(
t
)
, it is almost surely that
Sc
(0)
<
Nc
and
Sw
(0)
<
Nw
for
{
Sc
(
t
),
Sw
(
t
)}
G Q
and hence, in the matrix
(22)
we find that
G,
(
X
,
I
)
>
0
and
G
3 (
X
,
I
)
>
0.
Also
G
2
(
X
,
I
) =
G
4
(
X
,
I
) = (
G
5
(
X
,
I
) = (
G
6
(
X
,
I
) = 0. Hence, (
G
, (
X
,0)
>
0
for, where
i
=
1,2,...,6. Therefore condition II holds which shows that the disease free equilibrium point
Q
0
is globally asymptotically stable for
Ro
<
1
and hence the theorem (4.2) holds.
4.5. Stability analysis of Endemic Equilibrium Point, (EEP)
In this section, we apply the Lyapunov method and the LaSalle’s Invariant principle to prove the global stability of the endemic equilibrium point (EEP) of the model system (1). Now, consider a continuous and differentiable Lyapunov function defined as;
Where
ф
(
t
)
is a positive constant factor,
yt
is the
i
t
variable at compartment
i
and
yt
is the equilibrium point of the model at compartment
i
where
i
=
(1,2,...,8). Differentiating
L
(
t
)
w.
r
.
t
and substituting the constants of the model system (1) at the endemic equilibrium point into the function (23) we get;
t
hus from equation
(24)
we have,
where, and 8 = ~Ф1 (t)(l-- \ У1 Using the theorem (4.2) and the equation (24), the global stability holds only if dLtl < g. Now if r < 5 dt then dL(t) will be negative definite which implies that dL(t) < q But dL(t) = gonly if yt = yt for i = 1,2, dt dt . dt ... ,8. J dL (t)_ 1
I
y
1
,
y
2
,...,
y
8
e^
• °
Г
Hence the largest invariant set I dtis a singleton y . By the LaSalle’s invariant principle [12], it is then implies that y . is globally asymptotically stable in the invariant region if r < 5 and thus Ro > 1. We then establish the following Theorem;
Theorem 4.3
The Endemic Equilibrium Point
Q
* of a Newcastle disease transmission model (1) is globally asymptotically stable if
R
>
1.
In this section, numerical simulations of the mathematical model (1) are conducted to study the dynamics of ND in village chicken population in the absence of any intervention. For the simulation we use the value of
R
and other model parameter values as given in
t
able
2
.
t
he total population of village chicken and wild birds is assumed to be two thousand and five thousand respectively. Using the estimated parameter values given in
t
able
2
, we obtain the basic reproduction number,
Ro
=
0.5692732754
<
1 which by the theorem (4.2) the disease free equilibrium point
Q
0 is locally asymptotically stable. However, with the values given in the Table
2
and the estimated parameter value of
φ
=
0.003,
α
= 0.0002,
ψ
= 0.00083, and
a
= 0.0003 we obtain
R
=
6.867182099
>
1 at the endemic equilibrium point and by the theorem (4.3) , it follows that endemic equilibrium point
Q
*
= {
S
*
,
E
*
,
I
*
,
S
*
,
E
*
,
I
*
,
I
*
,
H
} exists and is globally asymptotically stable.
5.1. Variations of Population Variables on the Dynamics of ND Over Time
Table 2. Parameter Values of the Model System 1
Parameter
Parameter value
Source
γ
0.067
–
0
.
5
day
-
1
[1, 8, 20]
φ
0.003
day
-
1
Estimated
b
0.21
day
-
1
[1, 8]
α
c
0.001667
day
-
1
Estimated
α
w
0.00002
day
-
1
Estimated
ψ
0.00083
day
-
1
Estimated
µ
2.74
–
5.48
×
10
-
4
day
-
1
[14]
a
0.003
day
-
1
Estimated
δ
c
0.01989
day
-
1
[9]
ρ
0.9
Estimated
d
0.001
day
-
1
[6]
δ
w
0.025
day
-
1
[7]
µ
v
0.00219
day
-
1
[7]
k
10000 virus /
m
-
3
[6]
d
ifferent initial values and the given parameter values in
t
able
2
are used to illustrate numerical stability of the disease free equilibrium point
Q
0 and the endemic equilibrium point
Q
*
of the NDV transmission model system given in (1). With different initial values for
S
(
t
)
,
S
(
t
),
I
(
t
) and
H
(
t
),
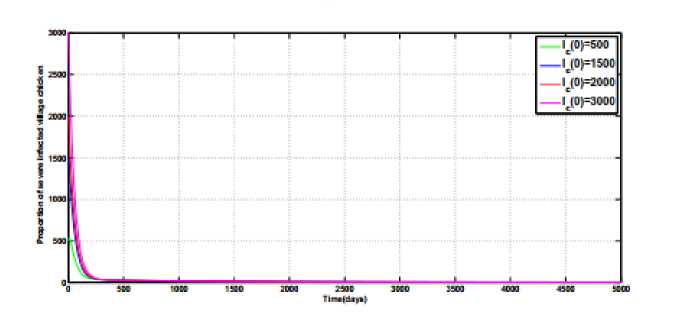
the curves for the severely infected village chicken
I
(
t
)
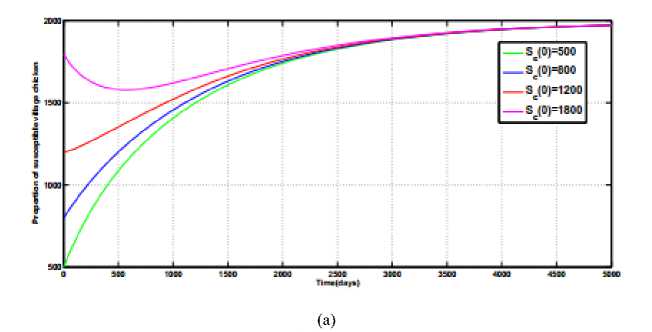
converges to zero along the time axis whilst susceptible population curves of the village chicken
S
(
t
)
converges to a unique point as shown in Fig .1 (a) and Fig.1 (b). This reveals that the disease free equilibrium point
Q
0
exists and is Stable for
R
< 1.
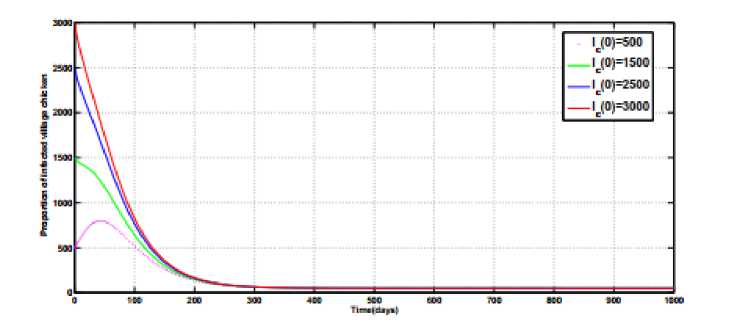
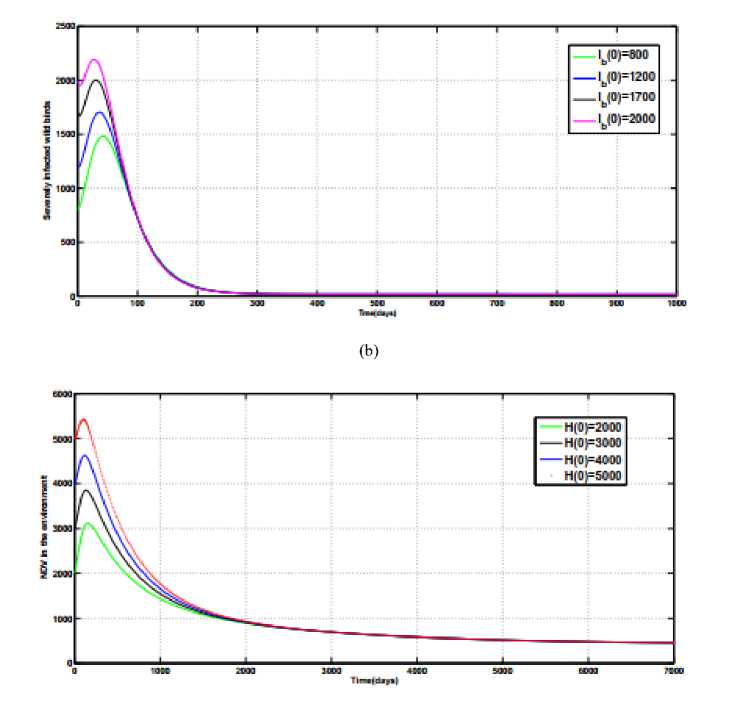
Fig.2(a), Fig.2(b) and Fig.2(c) illustrates the numerical simulations for the endemic equilibrium point of the model (1). Starting with different initial values and using the parameter values given in Table 1 and
φ
=
0.003 ,
α
=
0.0002,
ψ
= 0.00083 and
a
=
0.0003
for
R
>
1, the state variables
I
(
t
),
I
(
t
), and
H
(
t
), populations curves converges to the unique points above zero. The results of these figures prove that for
R
>
1 the endemic equilibrium point
Q
0
,
of the model system (1) exists and is stable.
(b)
Fig.1. Stability of the Disease Free Equilibrium Point, (DFEP) using the Parameter Values Given for
R
<
1.
(a) (c)
Fig.2.
Stability of endemic equilibrium point,
(
Q
*)
of the model system
(1)
using parameter values given in table for
R
>
1.
In this paper, we presented the stability analysis of the equilibrium points of the basic transmission model of ND for the free-range managed chicken without any control as developed by [6]. The model has two equilibria points, the disease free equilibrium point and the endemic equilibrium. The local stability of disease free equilibrium point is done analytically by using the Hurwitz Matrix method and we establish a theorem that under some given conditions the disease free equilibrium point is locally asymptotically stable. Using numerical simulations we confirmed that the disease free equilibrium point is locally asymptotically stable for Ro < 1.and the infected compartments converges to zero, while the susceptible compartment converges to a unique point above zero. Furthermore, we presented the analysis for the stability of the endemic equilibrium point of the model using the Lyapunov function and the Laselle’s theorem. The analysis shows that the endemic equilibrium point is globally asymptotically stable when Ro > 1. The existence of endemic equilibrium point was further confirmed numerically that regardless of the values of the initial condition of the state variables, the infected compartments converges to a unique point above zero which shows the persistent of disease in the population. Thus, the analysis presented in this paper shows that the transmission model for the ND among the village chicken population with the vital component of contaminated environment and wild birds is epidemiologically meaningful. This work provides an insight for looking different control strategies that considers the main agents in the dynamics of the ND. The controls will be helpful for the village chicken keepers in reducing the seasonal and periodic occurrence of the disease among village chicken population. Acknowledgment The authors would like to thank the Dar es salaam University College of Education (DUCE) for material support. Conflict of Interests No conflict of interests declared by author.
4. Analysis of the Model
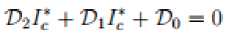
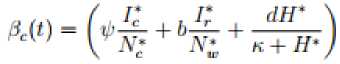
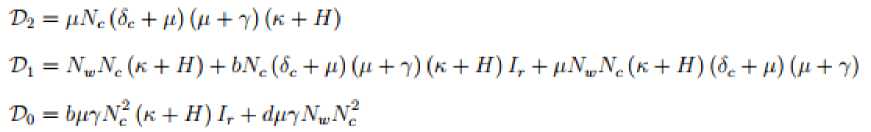
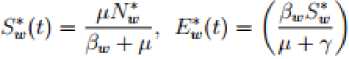
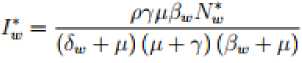
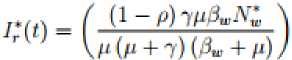
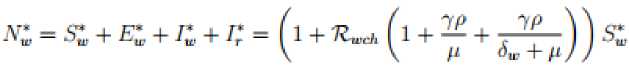
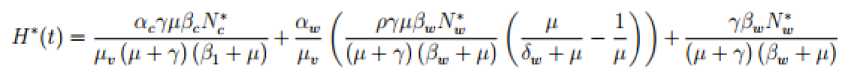
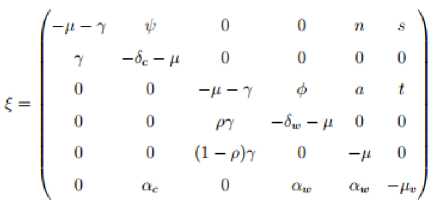
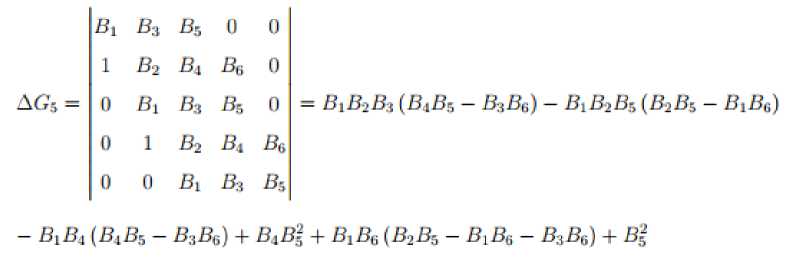
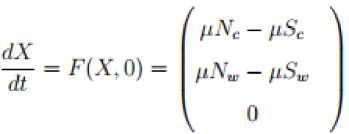
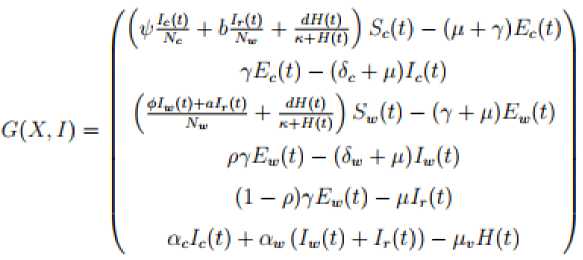
-p - 7
O
0
0
^^
7
—6C — //
0
0
0
0
0
0
-p - 7
0
fl
^^
B =
0
0
/>7
— ^w P
0
0
0
0
(i -ph
0
-p
0
0
^w
-Pv)
and
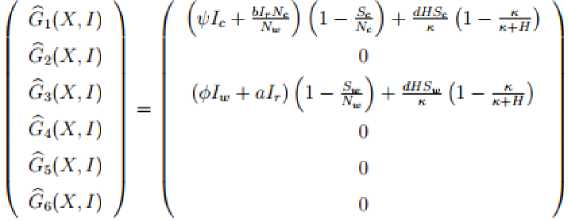
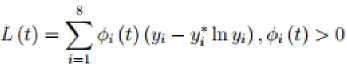
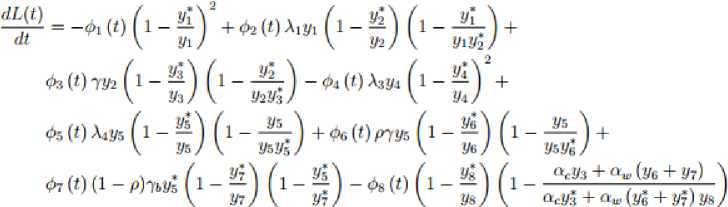
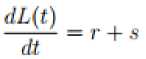
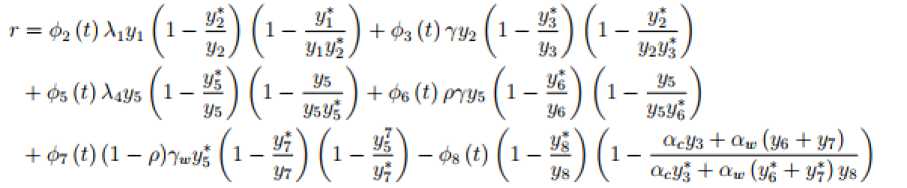
5. Results and Discussion
6. Conclusion
Список литературы Stability analysis of equilibrium points of newcastle disease model of village chicken in the presence of wild birds reservoir
- Alexander D. J., Bell J.G., and Alders R.G., A Technology Review: Newcastle Disease, with Special Emphasis on its Effect on Village Chick-ens. Food & Agriculture Org., 2004, no. 161.
- Anggriani N., Supriatna A., and Soewono E., “The existence and stability analysis of the equilibria in dengue disease infection model,” in Journal of Physics: Conference Series, vol. 622, no. 1. IOP Publishing, 2015, p. 012039.
- Anishchenko V.S., Vadivasova T.E., and Strelkova G.I., “Stability of dynamical systems: Linear approach,” in Deterministic Nonlinear Systems. Springer, 2014, pp.23–35.
- Brin M. and Stuck G., Introduction to Dynamical Systems. Cambridge university press, 2002.
- Castillo-Chavez C., Feng Z., and Huang W., “On the computation of and its role on global stability in mathematical approaches for emerging and re-emerging infectious diseases,” Mathematical Approaches for Emerging and Reemerging Infectious Diseases: an introduction, vol. 1, p. 229, 2002.
- Chuma F., Mwanga G.G., and Kajunguri D., “Modeling the role of wild birds and environment in the dynamics of newcastle disease in village chicken,” Asian Journal of Mathematics and Application, vol. 2018, no. 446, p. 23, 2018.
- Daut E.F., Lahodny G. Jr, Peterson M.J., and Ivanek R., “Interacting effects of Newcastle disease transmission and illegal trade on a wild population of white-winged parakeets in Peru: A modeling approach,” PloS One, vol. 11, no. 1, 2016.
- Dortmans J.C., Koch G., Rottier P. J., and Peeters B.P., “Virulence of newcastle disease virus: what is known far?” Veterinary Research, vol. 42, no. 1, p. 1, 2011.
- Hugo A., Makinde O.D., Kumar S., and Chibwana F.F., “Optimal control and cost effectiveness analysis for newcastle disease eco-epidemiological model in Tanzania,” Journal of Biological Dynamics, vol. 11, no. 1, pp. 190–209, 2017.
- Hunter J.K., “Introduction to dynamical systems,” UCDavis Mathematics MAT A, vol. 207, p. 2011, 2011.
- Kahuru J., Luboobi L., and Nkansah-Gyekye Y., “Stability analysis of the dynamics of tungiasis transmission in endemic areas,” Asian Journal of Mathematics and Applications, vol. 2017, 2017.
- La Salle J.P., The Stability of Dynamical Systems. SIAM, 1976.
- Lawal J., Jajere S., Mustapha M., Bello A., Wakil Y., Geidam Y., Ibrahim U., and Gulani I., “Prevalence of Newcastle disease in Gombe, northeastern Nigeria: A ten-year retrospective study (2004-2013),” British Microbiology Research Journal, vol. 6, no. 6, p. 367, 2015.
- Lucchetti J., Roy M., and Martcheva M., “An avian influenza model and its fit to human avian influenza cases,” Advances in Disease Epidemiology, Nova Science Publishers, New York, pp.1–30, 2009.
- Mafuta P., Mushanyu J., S. Mushayabasa, and Bhunu C.P., “Trans-mission dynamics of trichomoniasis in bisexuals without the E,” World Journal of Modelling and Simulation, vol. 9, no. 4, pp. 302–320, 2013.
- Mwanga G. G., “Mathematical modeling and optimal control of malaria,” A PhD Thesis, Acta Lappeenranta University, 2014.
- Mpeshe S.C., Luboobi L.S., and Nkansah-Gyekye Y., “Stability analysis of the rift valley fever dynamical model,” Journal of Mathematical and Computational Science, vol. 4, no. 4, p. 740, 2014.
- Nyerere N., Luboobi L., and Nkansah-Gyekye Y., “Bifurcation and stability analysis of the dynamics of tuberculosis model incorporating, vaccination, screening and treatment,” Communications in Mathematical biology and Neuroscience, vol. 2014, pp. Article–ID, 2014.
- Olaniyi S., Lawal M.A., and Obabiyi O.S., “Stability and sensitivity analysis of a deterministic epidemiological model with pseudo-recovery,” IAENG International Journal of Applied Mathematics, vol. 46, no. 2, pp. 160–167, 2016.
- Perry B., Kalpravidh W., Coleman P., Horst H., McDermott J., Randolph T., and Gleeson L., “The economic impact of foot and mouth disease and its control in South- East Asia: a preliminary assessment with special reference to Thailand.” Technical scientific Review, offce of Epizootic diseases, vol. 18, no. 2, pp. 478–497, 1999.
- Selemani M.A., Luboobi L.S., and Nkansah Gyekye Y., “On stability of the in-human host and in mosquito dynamics of malaria parasite,” Asian Journal of Mathematics and Applications, vol. 2016, no. 353, p. 23, 2016.
- Sharma S and Samanta G., “Stability analysis and optimal control of an epidemic model with vaccination,” International Journal of Biomathematics, vol.8, no.03, p. 1550030, 2015.
- Sharif A., Ahmad T., Umer M., Rehman A., Hussain Z.., “Prevention and control of newcastle disease,” International Journal of Agriculture Innovations and Research, vol. 3, no. 2, pp. 454–460, 2014.
- Tumwiine J., Mugisha J., and Luboobi L., “A host-vector model for malaria with infective immigrants,” Journal of Mathematical Analysis and Applications, vol. 361, no. 1, pp. 139–149, 2010.
- Wiggins S., Introduction to Applied Nonlinear Dynamical Systems and Chaos. Springer Science & Business Media, 2003, vol. 2.


