Стабилизация характеристик формирователей колебаний на основе многомодовых нелинейных динамических систем

Рассматривается подход к стабилизации многомодовых нелинейных динамических систем на примере формирователей колебаний, основанный на обобщенных многомодовых моделях. Показано, что наличие нескольких подходов к разделению нелинейной динамической системы на моды дает возможность рассмотреть решение задачи стабилизации с различных позиций. Приведено два подхода к решению задачи стабилизации динамической системы типа Лоренца, позволяющих обеспечить требуемое поведение системы.

Повышение надежности и безотказности работы формирователей колебаний в системах связи требует обеспечения стабилизации их параметров и характеристик при помощи внешних стабилизирующих воздействий. В зависимости от назначения формирователей колебаний, относящихся к многомодовым нелинейным динамическим системам (ДС), к модовому составу формируемых ими колебаний могут предъявляться различные требования. Так, в традиционных системах связи возникает задача стабилизации регулярных мод, а в перспективных широкополосных системах связи на основе эффектов хаотической динамики – хаотических мод. Для решения указанных задач требуется разработка системного подхода к стабилизации режимов поведения многомодовых ДС. Сопоставительный анализ существующих тенденций системного подхода к решению задач стабилизации ДС показывает, что наиболее целесообразным является его математическая формализация, учитывающая физические принципы построения реальных систем [1-2]. Среди существующих методов математического описания ДС следует выделить описание ДС на основе обобщенных многомодовых моделей [2-3]. Использование обобщенных многомодовых моделей в задачах стабилизации режимов поведения различных ДС может, на наш взгляд, служить основой для выявления новых подходов и методов стабилизации характеристик формирователей колебаний. Целью настоящей работы является разработка подходов к стабилизации режимов поведения и характеристик нелинейных систем и устройств формирования колебаний на основе обобщенных многомодовых моделей (ОММ).

Описание ДС в рамках ОММ предполагает разделение сложной системы на моды состояния, описывающие состояние ДС (например, структуру плазмы или параметры и характеристики формирователей колебаний) и моды поведения, описывающие динамику ДС (например, регулярный или хаотический режимы поведения сложной системы) [2; 9]. На рис. 1 представлена, уточненная по сравнению с [2; 9], обобщенная многомодовая модель ДС, учитывающая флуктуационные воздействия на моды поведения, ветвления в структуре и различия в характерных временах мод.

Рис. 1 НАМС – начальный ансамбль мод состояния; НАМП – начальный ансамбль мод поведения; ПрАМС _j – j -й промежуточный ансамбль мод состояния; ПрАМП _M – M -й промежуточный ансамбль мод поведения; • – начало ветвления в структуре обобщенной многомодовой модели; В_i – флуктуационные и внешние (регулирующие, стабилизирующие) воздействия

Следует отметить, что представление сложных ДС в виде набора мод (см. рис.1) не однозначно, причем для отдельных ДС возможны различные подходы к разделению на моды состояния и поведения. Поэтому требуется разработка средств разделения на моды состояния и поведения, адекватных задачам анализа и синтеза стабилизирующих воздействий. Наличие нескольких вариантов разделения ДС на моды дает возможность рассмотреть решение задачи стабилизации с различных позиций. Например, определить наиболее целесообразные для формирователей колебаний пути обеспечения требуемого (регулярного или стохастического) режима поведения и выявить параметры внешнего стабилизирующего воздействия. При этом основным критерием разделения ДС на отдельные моды являются малые величины связей между модами [1].

Для формирователей колебаний моду состояния возможно определить как тип колебаний, обуславливаемый параметрами и характеристиками (например, спектрально-корреляционных и вероятностных) устройства. В простейшем случае возможно различение двух типов мод состояния – регулярных и хаотических. На основе таких мод возможна однозначная диагностика режимов работы устройства. В общем случае возможно различение большего числа регулярных и хаотических мод, определяемых по указанным выше признакам. С другой стороны, под модой состояния возможно понимать параметры и характеристики ДС, описывающие динамику систем и устройств формирования колебаний, например, набор начальных условий, определяющих режим дальнейшего поведения формирователя.

Под модой поведения нелинейных систем и устройств формирования колебаний будем понимать закон (или совокупность законов) изменения ансамбля мод состояния, приводящие к изменению характера поведения ДС.

В рамках ОММ (см. рис.1) возможно выделить три постановки задачи стабилизации параметров и характеристик ДС:

• 1.    Обеспечение такого ансамбля мод состояния, который с учетом флуктуационных воздействий на моды поведения позволит обеспечить требуемый характер поведения ДС (статическое воздействие).

• 2.    Выявление параметров внешнего динамического воздействия на моды поведения, обеспечивающего требуемые режим поведения ДС при наличии флуктуаций.

• 3.    Обеспечение требуемой динамики сложной системы за счет выявления вида и параметров комбинационного (совместного статического и динамического) воздействия на ДС, учитывающего ветвления в структуре ОММ и различие в характерных временах мод.

В нелинейных устройствах и системах формирования колебаний с динамическим хаосом реализация первого подхода возможна за счет выбора параметров систем и параметров временной дискретизации. Второй подход реализуется, например, за счет введения стабилизирующих воздействий на параметры систем и параметры временной дискретизации.

Вопросы стабилизации хаотических мод на основе первого из указанных выше подходов за счет статического управления параметрами временной дискретизации для систем Ресслера, Анищенко-Астахова, Лоренца, Чуа с хаотической динамикой были рассмотрены в работе [10].

При этом диагностируемые моды различались по корреляционным характеристикам. Наиболее эффективным с точки зрения стабилизации хаотических мод состояния с заданными корреляционными характеристиками является управление параметрами временной дискретизации систем Анищенко-Астахова и Лоренца. Однако статическое управление не всегда реализуемо в формирователях колебаний, что обусловлено возможностью ухудшения некоторых параметров выходного колебания (например, выходной мощности). Наилучшим образом обеспечить требуемую структуру мод состояния возможно путем введения динамических стабилизирующих воздействий.

Необходимо отметить, что при выборе стратегий стабилизации мод поведения НАМП1 возможны ветвления (см. рис. 1) с переходом от НАМС1 не только к ПрАМС1, но и к ПрАМСj. В случае стабилизации хаотической моды динамической системы Лоренца-ДСЛ (1) за счет квази-резонансных воздействий на параметры систем и параметры временной дискретизации возможен переход не только к новой хаотической моде, но и к регулярной моде в зависимости от глубины стабилизирующего воздействия и начального ансамбля мод состояния. Поэтому одной из важнейших практических задач является обеспечение и стабилизация требуемых режимов этой ДС. В случае квазирезонансной модуляции параметров системы Лоренца с динамическим хаосом

• X = -o( t ) X + o( t ) Y ;

Y = r (t) X - Y - XZ; (1) Z = XY - b(t)Z, где X,Y,Z – переменные системы; r,b,σ – параметры системы Лоренца, широко используемой дляописаниятакихДСкаклазеры[5],формирова-тели колебаний на основе эффектов хаотической динамики [6], возможно получение хаотических мод с интервалами корреляции, варьируемыми в пределах одного порядка. При модуляции параметров временной дискретизации на основе ква-зирезонансных воздействий возможна вариация интервалов корреляции в пределах 20 раз [7].

Одним из критериев выбора параметров стабилизирующего воздействия является обеспечение требуемого режима ДС (с регулярными или хаотическими модами) при минимальных энергетических затратах на его стабилизацию с сокращением временного интервала стабилизации.

Необходимо отметить, что допущение многократных переходов между областями фазо- вого пространства с различными состояниями равновесия в системах с динамическим хаосом приводит к увеличению переходного процесса установления стабилизированного состояния системы. Однако многократные переходы позволяют повысить энергетическую эффективность управляющих стабилизирующих воздействий на нелинейные устройства и системы с хаотической динамикой [4].

Для повышения энергетической эффективности стабилизирующих воздействий необходимо обеспечивать минимальное удаление фазовой траектории от состояний равновесия системы в случае хаотической динамики системы Лоренца [4]. При минимальных отклонениях фазовых траекторий от состояний равновесия системы глубина стабилизирующих воздействий минимальна, а их энергетическая эффективность максимальна. Минимизация этих отклонений возможна двумя способами:

• 1.    Путем увеличения продолжительности временного интервала стабилизации при допущении многократных переходов между областями фазового пространства с различными состояниями равновесия [4].

• 2.    Путем обеспечения в многомодовой ДСЛ моды состояния с требуемыми начальными условиями в системе, обеспечивающих необходимую минимизацию отклонений фазовых траекторий от точек равновесия системы за времена, не превышающие период квазирезонансных колебаний в системе. Указанные моды состояния, как показано в работе, дают возможность сократить продолжительность временного интервала стабилизации на несколько порядков с одновременным повышением его энергетической эффективности.

Предлагаемое энергетически эффективное стабилизирующее воздействие на ДСЛ осуществлялось в работе путем задания особого начального ансамбля мод состояния (рис.1) при квази-периодических импульсных квазирезонансных воздействий (КР) вида

S = S ₀ + А cos to t , to>Q, 44 << 1 , / S o

где ξ0 - один из параметров динамической системы типа Лоренца r или b; fi - частота квазире-зонансных колебаний [4]. Оценка оптимальных параметров этих воздействий производилась по возможности стабилизации ДСЛ с динамическим хаосом при задании начальных условий (Xн,Yн,Zн) и действии на систему квазипериоди-ческих импульсных КР воздействий, с амплитудой m, достаточной для стабилизации ДСЛ без смен фазовой траекторией областей с различными состояниями равновесия, при допустимом начальном отклонении системы от положения равновесия, не превышающем 5% [8].

На основе численного моделирования ДСЛ (1) получена оценка границ области фазового пространства ДСЛ, определяющих моду состояния ДСЛ, обеспечивающую стабилизацию системы с минимальными энергозатратами на КР воздействия и сокращением продолжительности временного интервала стабилизации. Для значений R = 28, b = 8/3, с = 10 и А/ _G [ 0,01;0Д ] протяженность области начальных у ⁰ словий ДСЛ определяется установленными неравенствами:

26 <  X _н <  28;

4 < Y, < 17;

48 <  Z„ <  50.

н

При этом значение безразмерного времени

T t0 = стаб T , за которое достигается стабилизация ДСЛ, составляет не более t0 ~ 0,3 ^ 0,7; где Tкол – собственный период колебаний системы (1), Tстаб – время, за которое достигается стабилизация ДСЛ.

а)                            б)

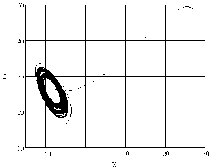
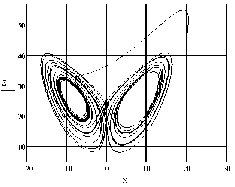
Рис. 2. Фазовый портрет ДСЛ (1) при

А/r₀ = 0.01; m = 0.1; |Р| = 57 :

• а)    X н = 27, Y _H = 12, Z „ = 49 ;

• б)    Xн = 20, Y _H = 28, Z „ = 46 .

Результаты численного моделирования ДСЛ (1), подвергаемой стабилизирующим КР воздействиям при различных модах состояния (задаваемых различными начальными условиями,рис. 2а и рис. 2б)пока-зали, что при сохранении величины радиус-вектора начальных отклонений от состояний равновесия

Iг| = 7X2 + YH + ZH2 , (3)

возможно обеспечение как регулярного (см. рис. 2а), так и хаотического (см. рис. 2б) режимов поведения рассматриваемой ДСЛ при одних и тех же уровнях КР воздействий.

Обеспечение начальных условий ДСЛ (1), принадлежащих ДСЛ (1) в выявленной области фазового пространства ( 26 <  X _н <  28,4 <  Y _H <  17, 48 < Z _h <  50) с заданием требуемой величины r , возможно за счет специального предварительного импульсного воздействия на систему. Примером этого воздействия может служить импульсная предыонизация плазмы в системах возбуждения газовых лазеров с несамостоятельным разрядом [10].

Анализ подходов к стабилизации нелинейных устройств и систем формирования колебаний на основе ОММ и различного разделения мод (состояния и поведения) в ДС позволяет сформулировать следующие выводы:

– на основе задания мод состояния, связанных с типом выходного колебания показано, что в случае квазирезонансной модуляции параметров системы Лоренца возможно получение хаотических мод с интервалами корреляции, варьируемыми в пределах одного порядка; при модуляции параметров временной дискретизации на основе квазирезонансных воздействий возможна вариация интервалов корреляции в пределах 20 раз;

– на основе задания моды состояния, определяемой начальными условиями формирователей колебаний на базе ДСЛ, установлена оптимальная мода состояния 26 <  X н <  28, 4 <  Y h <  17, 48 <  Z, <  50. При обеспечении попадания начальных условий в оптимальную моду состояния за счет предварительного однократного импульсного воздействия, и последующем действии на систему квази-периодических импульсных КР воздействий, возможно обеспечение требуемого стабильного режима поведения ДСЛ с минимальными энергетическими затратами на стабилизацию за интервалы времени,не превышающие период собственных колебаний ДС t ₀ ~ 0,3 ^ 0,7 .

Таким образом, многомодовый подход с разделением различных мод состояния и поведения является эффективным средством оптимизации стабилизирующих воздействий на нелинейные формирователи колебаний в системах связи на основе нелинейных ДС с хаотической динамикой. Обеспечение требуемого режима формирователей колебаний на базе систем с динамическим хаосом при помощи предлагаемых управляющих воздействий позволяет повысить их надежность и безотказность работы. Работа выполнена при поддержке Российского фонда фундаменталь- ных исследований (заявленный проект РФФИ №09-08-00268-а).