Стабилизация измерительной головки, подвешенной в трехстепенном кардановом подвесе

В работе решается

задача о стабилизации следующею механизма.

Измерительная головка а жестко связана с внутренней рамой Б • рданова подвеса сем. рисл^, которая может вращаться ;яносительно оси оо связанной с рамой в, вращающейся относительно оси о„о , связанной с внешней рамой Г. 8 свою очередь внешняя рама Г может вращаться относительно оси о о связанной с неподвижным основанием.

С неподвижным основатием лем абсолютную систему отсчета о<г- . Ось оу направим вертикально вниз, а оси о? и о?, расположи.: в горизонтальной плоскости так, чтобы система координат была правей.  0 внешней рамой подвеса  свяжем  систему  координат oxjz. Ось oz направим по оси вращения внешней рамы, ось ох„. по оси вращения средней рамы и осью oz дополним систему до правой  тройки.  Go средней рамой  свяжем  систему  координат

^^'z^z^z  Ось ОХ2 н^равим вдоль оси вращения средней рамы, ось oz - вдоль оси вращения внутренней рамы и осью oz, дополним систему до правой тройки. С внутренней раной свяжем систему координат ох y z . При этом ось ох натравим по оси вращения внутренней рамы, ось oz натравим таким образом, чтобы она была вертикальной евниз^ в положении, когда средняя рама горизонтальна, а внутренняя вертикальна. Ось ох дополняет систему до правой тройки.

Через «, ^, у, обозначим углы поворота с против часовой стрелки^ средней, внутренней и внешней рам соответственно.

Н-э^алэ отсчета е^т), Р=0, г^О определяется так, чтобы для него средняя рама занимала горизонтальное, внутренняя - вертикальное сложения, з система отсчета ox_ Y z совпадала с абсолютней 'ИСТ ЛОЛ C^'w.

У1 ^2'^3' 17

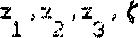
Рис.I.

Принимается, что рамки тюдЕзеса абсолютно жесткие, общин .центр тяжести головки и внутренней рамки, а также средней и внешней панки расположены в центре кардансва подвеса - в точке О Координатные оси системы ох урт совпадают с общими главными " ями жерчди измерительной головки и внучренней рамки, о -ксг’ртдыач стогом оч^с рг^ и ox y т - с главными (осями инерцс-о средней и внешней рамок, соответственно.

Управление механизмом осуществляется посредством вращательных моментов, действующих относительно осей вращения каждой из рамок.

Принимая углы л, р, у за обобщенные координаты и следуя работе ^г3:, выведем уравнения .движения механизмом. Заметим, что матрицы преобразования координат имеют следухяций зид:

А

Г COSV

- si п^

О

Si пу ccsy

О

О >

О

зг.

" 1

О

о

si Г1С1

~Sina СОЗСХ

cosp о si пр

<1 j

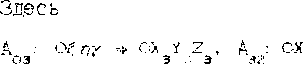
Обозначим через S”, о^П о^’- углевые скорости внутренней, средней и внешней рамок соответственно. Тогда абсолютные угловые скорости этих рамок п . ci , <5^ будут вычисляться по формулам

> = О

Э 3

> -= а 2       3

О = Q + О'

Пусть ср. , о .г^- - проекции вектора п в системе координат ох у z. Выразим эти координаты через обощенные координаты и обегенные скорости. Последовательно имеем:

Наймуст Д. В. , Чветтов Г . А

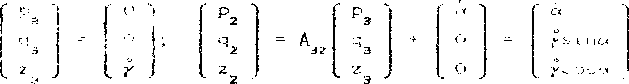
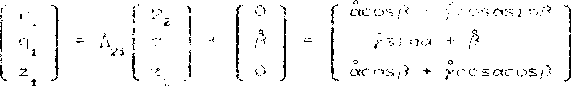
Обозначим через а , В, , С главные моменты инерг соответствующих рэмпк относительно осей ох оу , oz . 1=1, а. Запишем кинетические моменты каждой из рамок относительно цент кард-.-чова подвеса в проекциях на оси i -й системы координат, учетом формул С4> имеем:

ати у а

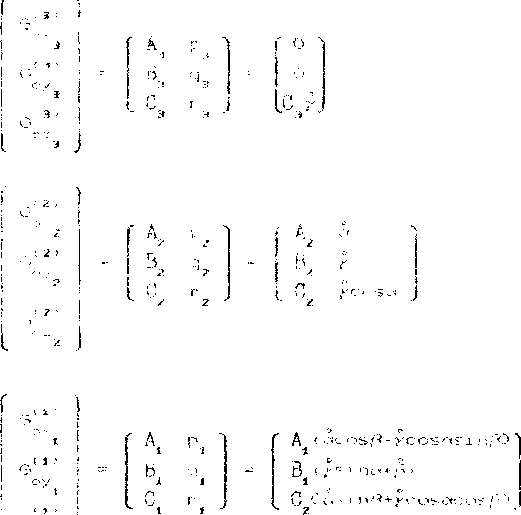
Обозначим через n*³’, n⁴²^ й'¹’ главные моменты внешних по отношению, соответственно, ко всему механизму, средней л внутренней с совместно с измерительной головкой) рамке и внутренней с совместно с измерительной головкой) рамке сил.

Заметим, что м'э> = и ,    ,ы’2> = и . ы“’ = и , се)

Z3 3       х2 2 yl      1

а проекции г'^, ы*^3>, n^²’. n^’, iT^ представляют собой моменты нормальных реакций опор о_до , о о₂. о о относительно соответствующих осей.

Запишем теорему об изменении кинетического момента по „'’ношению к каждой из рамок. На основании 3-го закона Ньютона имеем:

,<г,э> о гт<э> г42'° dtdt

N

сг>

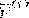
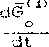
f3°’.

С 7)

Используя понятие локальной производной, перепишем равенства с?):

На основании формул С4), со из уравнений се) выводим:

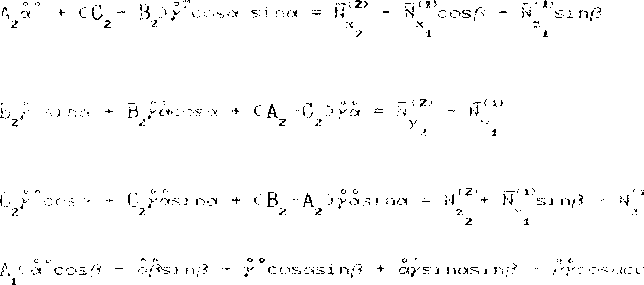
В D/ s 1 пу ^лВи <^^si н(3*у<.

N

Ox

Из уравнения с 9d исключаем величины ы'", и'¹’, н'²\ ы^:

\v , м<3' и полученные уравнения разрешаем относительно старших з v з производных:

0 F Ci + n‘^Z>P Q - FP О - N^i3>P о + ЕС Р * г4^!5>п Р о О 13 1 х2 3 1       2 1 кЗ 2 \      3 2 yl ’3 2

Т

OCR Р - R Р ) * О F R 12 3 ЭХ    3 2 1

-R I СР С * n'^'P О - FP О - N ^3>Р О ♦ ЕО Р + N¹ *’с Р ) 1     3 1 х2 3 1        2 1     23  2 1      3 2 VI 3 2

Q ( Q С R Р 1  12 3

3 2

* О Р р 1 а 1

С Е+ N '1' О t Q С Р Р - R Р 0 + О Р R 1 у 1      1   2 3     3 2      3 2 1

С 1 СО.

Q Г Q С R Р 112 3

Р Р 3 Z

•РЕЗ

3 2 1

<С+Ы^!2’:>[С>,Z>P Q ■ FP С -'            х2 1   2 3   3 2     3  2  1 Z 3 1 X г 3 Л 2 4

? .= ---------------------------------------------------

Р Г с ' Р Р - R Р > - о Р R ]

2                     3  2       "3 21

Г4 ' Р z з

г Р + Н^(1>О Г- 3 Э 2 у 3 2

Г (OCR Р

Z 12 Э

Р -О > О -В . Р - В sina, Р = А * A cc^;^Z(3 + С si п² . О

R -С С -А ? со< ctsi rJ3cos(3 ъ Р —v С - A )cos/i'Si i:^c;?S6v, С - В Sina, 2  11            3  11            31

R =С В + В )sin^Za + С +СС + С eos.²13   A sin^Z^jcos^Za,

3      2      1                    3      2      11

Е --В yck -СА^- С DCacos^ ^ fcosacosfDCacos/? - ^ccs^si п/?^

х >²(В + В “ С - С cos,²<3 Д si ji²/O cos

12   2   1          1

yct'S^sin/? +■ >/<[ cos2 [$< Д — r з В ^) 3      /КС + В - A )]cosa illiii

F — ^a^sinncosatB - С + В ' A sinZf^ - C cos2/?) - a Ac: osx г 2 t ii х! г? *СС — A )Ccos2/? - sin2/?)) ™ 2$xcos/5si nf^cos2 оС A - C j - c/sinflcostfsinaCA - C 3

C 11

Уравнения ciod, (id будем называть полной механизма.

моделью функции система

Сформулируем зада ч стабилизации.

Задача: определив управления и. i-i.a.a как фазового вектора са./з.у ,а,^То так, чтобы дифференциальных уравнений сю), сш после подстановки в нее найденных управлений, была ассимптотически устойчива. При этом дтго. мнительно требуется, чтобы отклонение фазовых координат от нуля уменьшилось в заданное число раз по отношению к начальному по истечению фиксированного промежутка времени.

Решение этой задачи проведем на базе анализа линеаризованных в окрестности начала координат уравнений с юз, сю, которые после отбрасывания членов высшего порядка малости принимают вид:

В выражении ci4:> величины s . д . 1=ГГз - суть постоянные коэффициенты, найденные из условия отрицательности мнимых частей корней характеристических уравнений для системы ог:-, в которой управления и, . >-з,г,з заменены по формулам яг-, а также условия достаточной малости отклонения фазового вектора от нуля к зчданн‘ ‘му моменту времени.

В частности, для случая, когда т=о. i сек., начальные at, рае

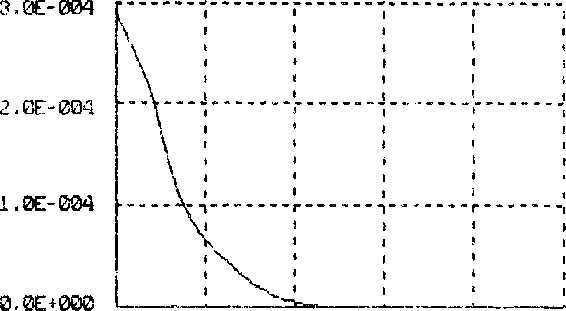
0.00   0.02   0.04   0.06   0.08    0.10

Рис.

а

об, рад

5.0Е-003

0.0Е+000

-5.0Е-003

-1.0Е-002

-1.5Е-002

-2.2Е-002

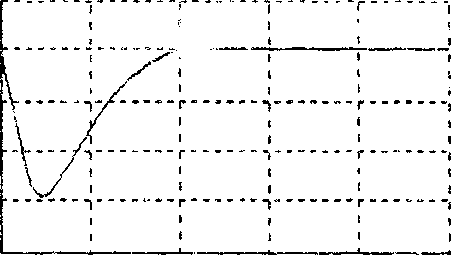
0.00   0.02   0.04   0.06   0.08   0.10

Рис. 26

4 =jO-Z-J , A ^W-1O²-J , z-ao. 0-150 '15?

Из теории устойчив .;оти известно сем, например газ;., что если корни характеристичес ..„-гп уравнения линеаризированной задачи имеют строго отрицательные мнимые части, то и нелинейная задача ассимптотически устойчива. Это ггредложение было подтверждено ■злеленными расчетами с полной моделью ою, (и>, в которой управления и с1=Г7зб опредвлядись по формулам <14?, сю?..

Численное решение указанной задачи иллюстрируется графическими зависимостями угловых координат и соответствующих скоростей сем. рис. 2а-б?. В качестве примера приводятся графики юордина'1’ а, а с две другие пары оообщенлых координат имеют аналогичную качественную интерпретацию.

Из графиков га-б видно, что где-то в районе t=O.OB сек. с расчетное время стабилизации положения измерит с явной головки г=о.1 сек.) численные значения обобщенных координат укладываются в требуемую по отклонениям погрешность <напомним, что она составляет 1% от начальных условий.' и в точке т-0.1 сек. имеет’ значение порядка ю"⁷, что соответствует решенигэ поставленной задачи.

Таким образом. выбранные для линеаризованной (исгео/ управления вида ci4? с коэффиг^нтами обеспечивакл' геыен-’о задачи стабилизации для исходной нелинейной модели.