Стабилизация космического аппарата с несимметричной упругой конструкцией на геостационарной орбите

Рассматривается космический аппарат (КА) с несимметричной упругой конструкцией на геостационарной орбите (ГСО), в частности геостационарный информационный спутник (связи, геодезии, землеобзора и др.) c крупногабаритными упругими навесными конструктивными элементами – антеннами, рефлекторами и панелями солнечных батарей (СБ), либо космический робот с несимметрично распределённой упругой полезной нагрузкой. В процессе движения такого КА с длительным сроком активного существования (САС) нормаль к плоскости панелей СБ направлена на Солнце, изменяются тензор инерции и масса КА за счет расхода топлива для удержания его на ГСО. В системе управления движением (СУД) космического аппарата применяются астроинерциальная система определения углового положения (СОУП) и аппаратура спутниковой навигации, кластер электромеханических исполнительных органов (ЭМИО) в виде двигателей-маховиков (ДМ) либо гиродинов (ГД), а также двигательная установка (ДУ) с широтно-импульсной модуляцией (ШИМ) тяги реактивных двигателей (РД), которая используется также для разгрузки кластера ЭМИО от накопленного кинетического момента (КМ). Несимметричность конструкции КА приводит к существенному темпу накопления импульса

возмущающего момента из-за влияния сил солнечного давления (ССД), что создает проблемы разгрузки кластера ЭМИО от накопленного КМ и удержания КА на ГСО при длительном САС. Указанные проблемы управления движением КА изучаются [1], в том числе с выполнением экспериментов в космических условиях [2].

Если принять конструкцию КА в виде твердого тела, то при стандартных обозначениях модель динамики его пространственного движения имеет общеизвестный вид [3]

m v-Lx о -ox(Lxto) = R;

Lxv + K + tox K = M , где m - масса КА; v - вектор скорости его по*

ступательного движения, v = v +tox v , где *

( • ) - символ локальной производной по времени; L = m р _с - вектор статического момента; вектор р _с представляет расположение центра масс C в связанной системы координат (ССК); K = J to - вектор КМ, R и M - главные векторы внешних сил и моментов, представленные в полюсе O ССК. Физически эти векторы формируются в отношении центра масс C , что учитывается при расчете векторов R и M относительно полюса O . С другой стороны, в силу технологических условий установки РД на корпусе КА ось действия суммарной тяги КДУ проходит точно через полюс O и при коррекции орбитального движения КА возникает возмущающий момент ДУ. При этом СУД обеспечивает стабилизацию требуемого углового движения спутника и в кластере ЭМИО с вектором КМ H происходит накопление вектора суммарного КМ G = K + H механической системы, обусловленного всеми видами внешних возмущающих моментов.

Для геостационарных КА при разгрузке кластера ЭМИО от накопленного КМ и коррекции орбитального движения спутника иногда применяется ДУ на основе только электрореактив-ных двигателей (ЭРД). Одновременное создание внешних сил и моментов с помощью ЭРД является актуальной проблемой управления движением информационных спутников [4], для ее решения разработаны алгоритмы управления ДУ на основе восьми ЭРД с ШИМ их тяги [5,6]. Алгоритмы фильтрации измерений, полетной юстировки и калибровки астроинерциальной СОУП описаны в [7] –[9]. В статье представляются подходы к исследованию первоочередных задач: 1) анализ потребной области вариации КМ кластера ЭМИО для компенсации влияния ССД; 2) синтез цифрового управления кластером ЭМИО; 3) анализ динамики СУД в режиме угловой стабилизации при решении целевых задач.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ

Вводятся инерциальная (ИСК), связанная (ССК) Oxyz и орбитальная (ОСК) Oxoyozo системы координат с началом в полюсе O, который совпадает с номинальным положением центра масс C КА. Положение ССК относительно ИСК определяется кватернионом Λ , относительно ОСК - вектором-столбцом ф = {ф1,ф2,ф3} , составленном из углов рыскания ф1 = V, крена ф2 = ф и тангажа ф3 = 0, которые используются в последовательности 132 при индексах осей i = 1,2,3. Далее применяются обозначения [•] - строка, {•}- столбец, (•)* - символ транспонирования, [ax] - косо-симметричная матрица на основе вектора a .

Схема геостационарного информационного спутника с несимметричной конструкцией представлена на рис. 1, а схемы минимальноизбыточных кластеров ЭМИО на основе ДМ и ГД с областями вариации их нормированного КМ – на рис. 2 и рис. 3 соответственно.

Кинематические уравнение для кватерниона Л имеет вид Л = Л ° to / 2 . Если Л ^p ( t ) и ю ^p ( t ) представляют закон наведения КА в ИСК, то кватернион погрешности Е ( t ) = (е₀( t ), е ( t )) = Л ^p ( t ) ° Л ( t ) , угловые погрешности определяются столбцом 8ф = { 8ф i } = 2е ₀ е и матрицей C ^e = 1 ₃ - 2 [ e x ] Q e , где Q _e = 1 ₃ e ₀ + [ e x ] , а вектор погрешности стабилизации скорости 8 to ( t ) = { 8to _z .} = to ( t ) - C ^e to ^p ( t ) .

В ССК оси вращения четырёх ДМ в составе кластера по схеме General Electric ( GE ) располагаются на поверхности конуса с углом полу-раствора Y , рис. 2. Столбцы H = { H i } и h = { h _p } , h = J r Q , p = 1 ^ 4 представляют векторы КМ ^p класте ^p ра ДМ и отдельных четырех ДМ, которые связаны соотношением H = A _Y h , где прямоугольная матрица A _γ составлена из ортов осей вращения ДМ в ССК. Угловые скорости Ω _p и ускорения Ω _p всех четырех ДМ с одинаковым моментом инерции J _r ограничены по модулю. Реактивный момент класте-

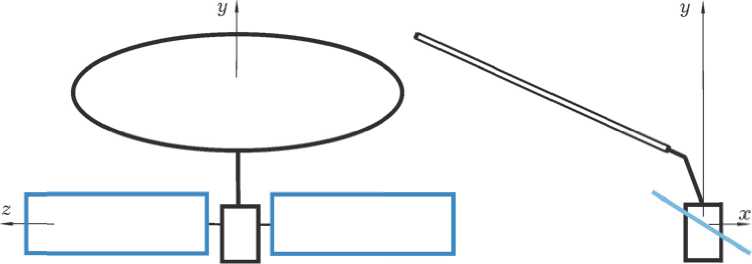
Рис. 1. Схема геостационарного спутника с несимметричной конструкцией

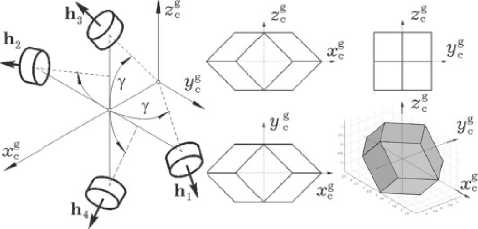
Рис. 2. Схема GE кластера ДМ

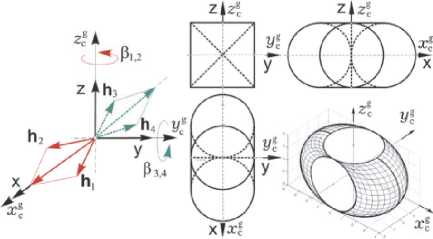
Рис. 3. Схема 2-SPE кластера ГД

ра ДМ М r = - Н =- J r X ^ Q со столбцом Q = { Q _p } угловых ускорений ДМ принимается в виде M r = — A _Y ( m — m ^f ) , где m = { m p } и m = { m p } - столбцы моментов управления и сухого трения по осям вращения ДМ.

Кластер четырех ГД c одинаковым модулем КМ h^g посхеме Scissored Pair Ensemble ( 2-SPE ), рис. 3, имеет вектор КМ Н ( Р ) = { Н , } = h g L h p ( Р p ) , где h _p ( в _p ) , p = 1 ^ 4 , является ортом КМ p -го ГД и столбец р = { р } составлен из углов поворота ГД относительн ^p о осей их подвеса на корпусе КА. Кластер ГД формирует управляющий момент М g ( р , р ) = - Н * = - h g X _h ( р ) u g ; р = u g , где матрица Якоби A _h( P ) = 5 h / д р и «управлением» считается вектор-столбец u g = {u⁸ g } с компонентами u_p^g командных скоростей поворота гирокожухов ГД, ограниченных по модулю.

Для исключения избыточности указанных кластеров ЭМИО применяются явные законы их настройки. Так, в [10] описан закон настройки кластера четырех ГД, гарантирующий отсутствие сингулярных состояний в «рабочей» части области вариации его КМ.

Модель пространственного движения КА с упругими подвижными элементами конструкции подробно представлена в [11,12], поэтому без детализации обозначений модель динамики КА приближенно принимается в векторно-матричном виде

m I 3 — [ L x ] [ L x ]      J _ m q     d q	M , 1 D , A q	" v " to _ _
to x ( L x го	• - 2 L ) + R		1	.        (1)
= — to x G + M to + M c + M _— A q ( V q q + W q q ) + M p _

Здесь q – столбец упругих перемещений конструкции; M _q и D _q – матрицы влияния упругих перемещений на движение КА, A ^q , V _q и W _q – матрицы обобщенных масс, демпфирования и нормированной жесткости конструкции КА; G = К + Н + D q q ; L = M q q ; M ^ и M P -векторы моментов, обусловленных угловым перемещением панелей СБ;

R = R gr + R5 + R e и М = М gr + М5 + М e представляют векторы внешних сил и моментов, обусловленных гравитационным (индекс gr) влиянием Земли, Луны и Солнца, влиянием ССД (индекс s) и работой ДУ на основе ЭРД (индекс e); вектор Mc представляет управляющий момент ЭМИО, при этом M c = M r для кластера четырех ДМ и M c = M g для кластера четырех ГД.

ПОТРЕБНАЯ ОБЛАСТЬ ВАРИАЦИИ КМ КЛАСТЕРА ЭМИО

Силы солнечного давления являются основным внешним возмущением при движе-

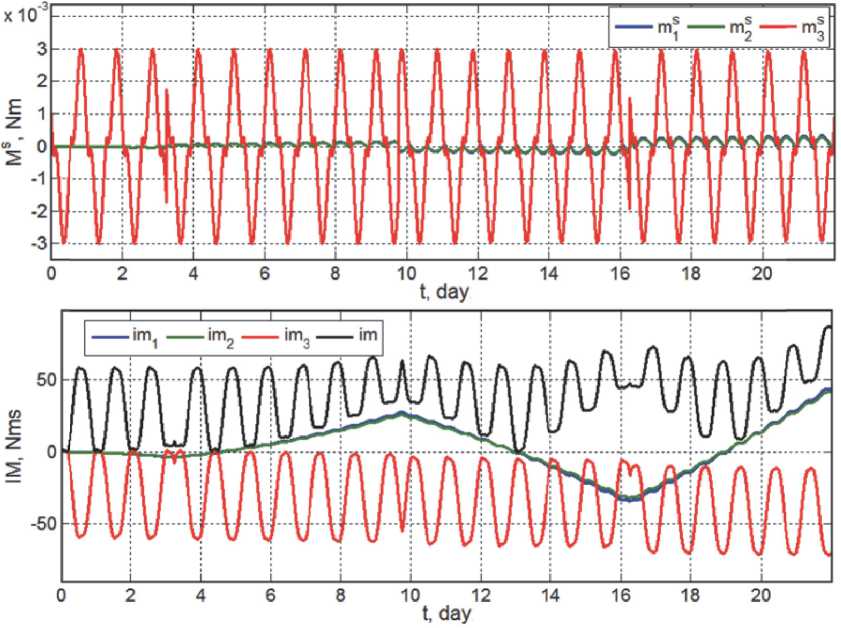
Рис. 4. Момент и импульс момента ССД, три недели после весеннего равноденствия: отметка 0 суток соответствует времени 20.03.2019 12:00:00

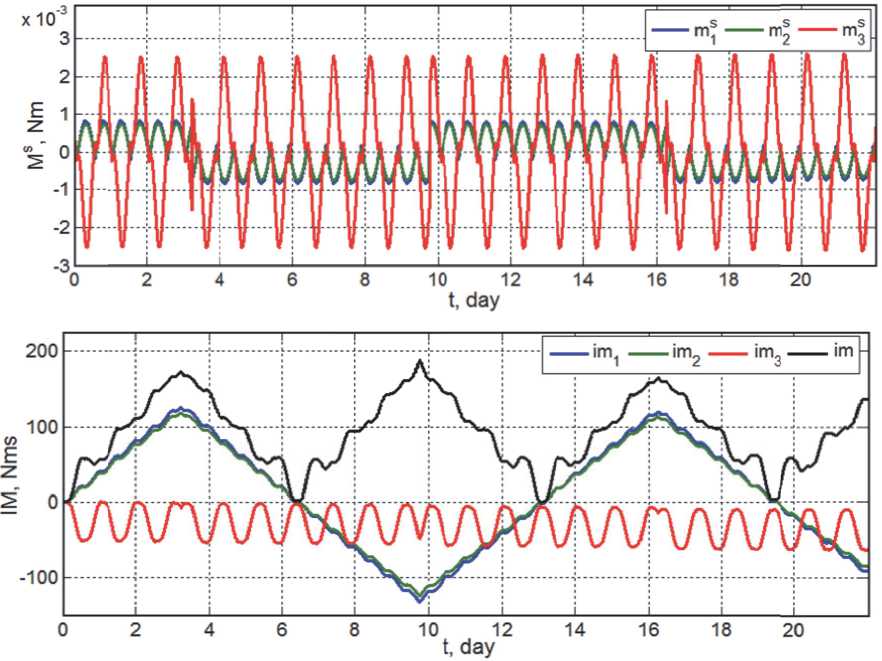
Рис. 5. Момент и импульс момента ССД, три недели после зимнего солнцестояния: отметка 0 суток соответствует времени 21.12.2019 12:00:00

нии КА по ГСО. Для оценки потребной области вариации КМ кластера ЭМИО с компенсацией влияния ССД рассмотрим режим угловой стабилизации ССК спутника с несимметричной конструкцией (рис. 1) в ОСК, когда углы ф i = 0 . При этом предлагается с периодичностью порядка 1 недели выполнять разворот корпуса спутника на угол 180 градусов относительно оси O x ССК, совпадающей в данном случае с осью O x ⁰ ОСК. Будем считать заданными в ССК положение центра давления (1, - 1.8, 0) м двух панелей СБ суммарной площадью 60 кв.м, нормаль к плоскости которых регулярно наводится на Солнце, и положение центра давления ( - 4.5,5.4, 0) м рефлектора с диаметром 12 м, для простоты с одинаковыми отражающими свойствами его основной и тыльной сторон. Расчеты сил и моментов ССД выполнены на основе известной методики [13], результаты представлены на рис. 4 и рис. 5 для векторов момента ССД M ⁵ = {m S } и импульса момента ССД IM ⁵ = IM = {im i } с модулем | IM | = im , когда указанный разворот выполняется с периодичностью 6.5 суток. В этих и последующих рисунках синий цвет связан с осью рыскания O x , зеленый цвет - с осью крена O у , а красный цвет - с осью тангажа O z .

Анализ результатов для импульса момента только ССД позволяет оценить потребную об- ласть вариации КМ кластера ЭМИО в виде шара радиусом 200 Нмс при выполнении указанных разворотов с периодичностью 6.5 суток. В целом потребная область вариации КМ ЭМИО оценивается шаром с радиусом 265 Нмс, что обеспечивается как кластером ДМ с максимальными значениями КМ 150 Нмс, так и кластером ГД с модулем КМ 150 Нмс. Требование к размерам потребной области вариации КМ ЭМИО можно уменьшить при выполнении разворотов корпуса КА с периодичностью « 3 суток, если это допустимо для решения целевых задач спутника.

АЛГОРИТМЫ ЦИФРОВОГО УПРАВЛЕНИЯ КЛАСТЕРОМ ЭМИО

Измерение углового положения и вектора угловой скорости корпуса КА выполняется СОУП в моменты времени t_s = sT q , s е N₀ = [0,1,2,...) с периодом T_q ≤ T_u , кратным периоду T_u цифрового управления кластером ЭМИО. В эти же моменты времени t_s измеряются координаты ЭМИО – векторы-столбцы угловых скоростей ДМ Ω _s либо углов поворота β _s ГД.

Для информационных спутников с симметричной упругой конструкцией хорошо зарекомендовал себя метод [11,12] формирования командного вектора Mk, k е N0 для кластера ЭМИО, который затем распределяется по явным аналитическим соотношениям для цифрового управления каждым ДМ либо ГД с периодом Tu . Здесь выполняется фильтрация значений векторов рассогласования εs = -δφs = -2e0ses , угловой скорости ωs , координат ЭМИО Ωs либо βs , которые используются для получения оценок Hfk, Gfk = Jωfk +Hfk и затем при формировании вектора Mck управления кластером ДМ gk+1 = Bgk + Ce,; mk = К (gk + Pek);

Mc = ®f xG^ + J(C0p + [C:topX]to^ + mj,,_ k k k k к k к k k где при обозначениях du ≡ 2/Tu , a = (du T1 -1)/( du T1 +1) элементы диагональных матриц B , P и C вычисляются в виде a = (duTi -1) /(duTi +1); p = (1 - b)/(1 - a) ; c ≡ p(b - a) с настраиваемыми параметрами τ1 , τ2 и k в составе диагональной матрицы K .

Закон управления (2) является робастным и обеспечивает заданное качество переходных процессов для произвольного положения панелей СБ и допустимого значения накопленного КМ, а также слабую вариацию показателей качества при изменениях тензора инерции до ± 5 % и низших частот колебаний конструкции до ± 10% от номинальных значений. Однако в случае информационных спутников с несимметричной упругой конструкцией на ГСО этот закон допускает неприемлемое квазистатиче-ское угловое рассогласование, что обусловлено существенными значениями момента ССД M ^s с модулем ≈ 0.003 Нм. Для устранения этого недостатка закон управления (2) был модифицирован в двух аспектах:

• 1)    на борту спутника на основе доступных измерений формируется оценка вектора момента ССД M ^s _k с периодом T_u , где по явным аналитическим соотношениям вычисляются расчетные моменты ССД от рефлектора, панелей СБ и корпуса КА с учетом возможного их взаимного затенения, и далее полученная оценка вектора M ^ˆ _k ^s добавляется с обратным знаком в правую часть последнего соотношения в (2), что обеспе-

• чивает прямую компенсация влияния возмущающего момента ССД с точностью порядка 10%;

• 2)    при дискретном формировании управления дополнительно используется векторный дискретный изодром с единичным коэффициентом усиления и постоянной времени τ₀ >  τ₁ , что обеспечивает астатизм первого порядка относительно внешнего возмущающего момента в каждом канале стабилизации углового движения спутника.

АНАЛИЗ ДИНАМИКИ СУД В РЕЖИМЕ СТАБИЛИЗАЦИИ

Динамический анализ нелинейной непрерывно-дискретной модели СУД выполнен на основе компьютерной имитации средствами программной системы SIRUIS-S [14].

Анализировался режим угловой стабилизации информационного спутника с описанной выше несимметричной упругой конструкцией в ОСК при цифровом управлении как кластером четырех ДМ, так и кластером четырех ГД с периодом управления T_u = 4 с при периоде измерения T_q = 1 с.

На рис. 6 приведены переходные процессы в СУД при начальных условиях фi (0) = 60 угл. сек и рассогласованиях по угловой скорости 5toi (0) = 0. При этом для каждого ДМ на основе алгоритмов [6] выполнялись текущая идентификация моментов сил сухого трения mfp с предельными значениями ± 0.002 Нм f с получением оценок mp и алгоритмическая компенсация влияния этих моментов. На рис. 7 представлены погрешности стабилизации корпуса упругого КА по углам, рассогласования по угловым скоростям, а также погрешность δm1f = m1f - mˆ 1f идентификации момента m1f сил сухого трения по оси вращения первого ДМ в процессе изменения скорости его вращения в окрестности момента времени t = 410 с.

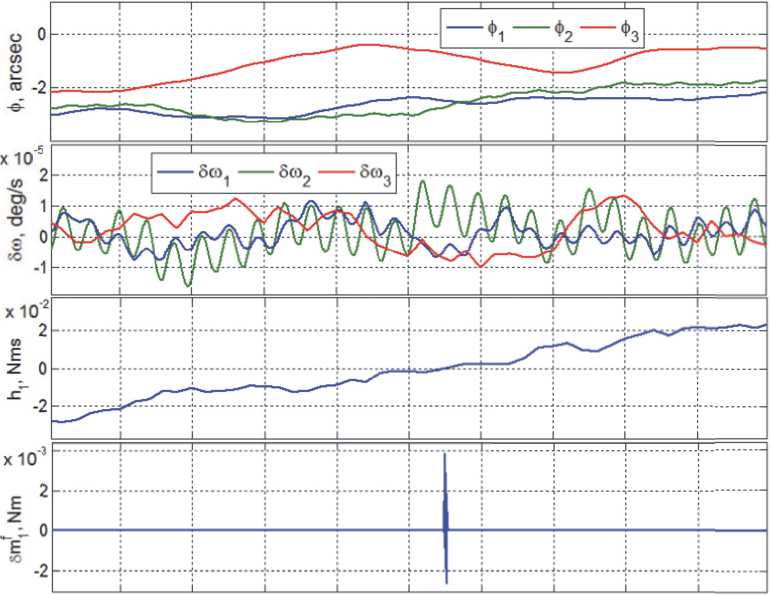
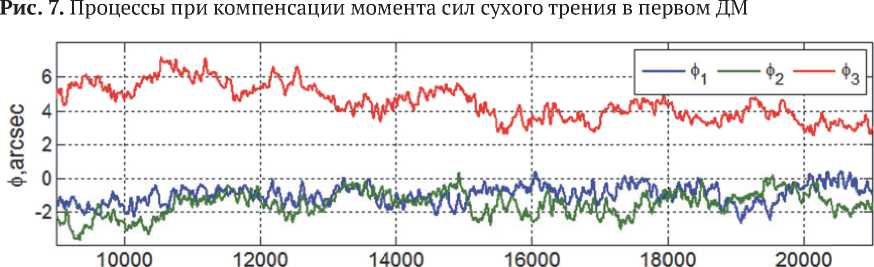
Рис. 8 и рис. 9 представляют погрешности угловой стабилизации КА в процессе завершения переходного процесса. Здесь следует обра-

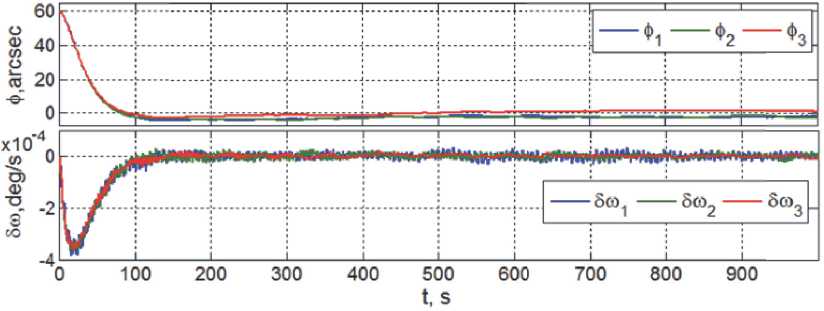
Рис. 6. Переходные процессы в СУД при заданных начальных условиях

320    340    360    380    400    420    440    460    480

t,S

t, S

Рис. 8. Переходные процессы при включении дискретного изодрома

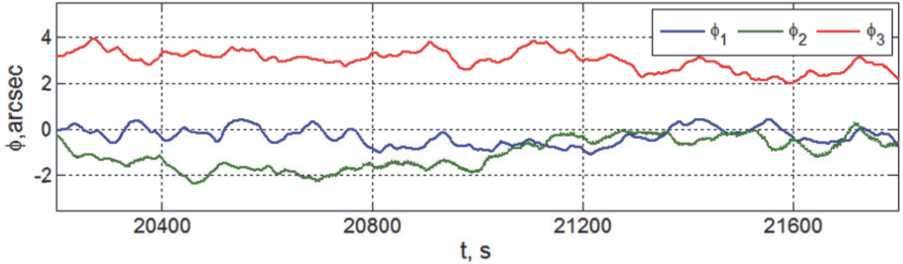
Рис. 9. Угловые рассогласования в установившемся режиме угловой стабилизации спутника

тить особое внимание на переходный процесс по каналу тангажа (красный цвет), приведенный на рис. 9, где демонстрируется эффект компенсации гравитационного момента, вносимый дискретным изодромом с постоянной времени τ₀ = 8 τ₁

ЗАКЛЮЧЕНИЕ

Кратко рассмотрены новые актуальные задачи исследования СУД информационного спутника с несимметричной конструкцией на ГСО. При 15-летней длительности потребного

САС спутника и существенном влиянии внешнего возмущающего момента как от сил солнечного давления, так и гравитационных сил, первоочередная задача состояла в разработке рационального подхода, позволяющего исключить большие затраты рабочего тела ДУ для разгрузки кластера ЭМИО от накопленного кинетического момента.

В предложенном подходе для частичной компенсации влияния ССД предусмотрено выполнение разворота корпуса спутника на угол 180 градусов вокруг оси O x ССК с периодичностью около 1 недели. Такой разворот необходимо выполнять в течение получаса с обеспечением слабого возбуждения упругих колебаний конструкции спутника и гладкого сопряжения краевых условий поворотного маневра по кватерниону ориентации, векторам угловой скорости и углового ускорения, а также по производной вектора углового ускорения в момент времени завершения поворотного маневра.

Получены оценки размеров потребной области вариации кинетического момента кластера ЭМИО, необходимых для поглощения возмущающих моментов как только от сил солнечного давления, так и с учетом влияния гравитационных сил. Полученные результаты послужили основанием для определения потребных значений кинетических моментов кластеров ЭМИО с применением как двигателей-маховиков, так и гиродинов.

Разработаны алгоритмы цифрового управления кластерами ЭМИО в классе комбинированных законов управления, где используются текущая оценка вектора возмущающего момента от сил солнечного давления и векторный дискретный изодром, который обеспечивает аста-тизм первого порядка относительно внешнего возмущающего момента. В случае использования кластера двигателей-маховиков применены дискретные алгоритмы идентификации и автоматической компенсации влияния моментов сил сухого трения по осям их вращения.

Выполнен предварительный динамический анализ СУД в режиме угловой стабилизации КА в орбитальной системе координат и приведены результаты, которые демонстрируют эффективность разработанных алгоритмов. Для информационного геостационарного КА с крупногабаритной несимметричной конструкцией имеются также другие важные проблемы динамического проектирования СУД, где особо следует выделить два аспекта:

• 1)    расположение центра масс КА относительно полюса ССК изменяется как за счет эпизодического расхода топлива двигательной установки, так и из-за колебаний крупногабаритного рефлектора, вынесенного на протяженной упругой штанге относительно корпуса спутника;

• 2)    измерительные системы и исполнительные органы СУД «привязаны» к ССК, ориентация которой отличается от углового положения крупногабаритного рефлектора, применяемого для информационного обслуживания заданных наземных объектов.

Исследование этих важных проблем предусмотрено в дальнейшей работе авторов.