Стабилизация орбитальной ориентации космического аппарата

В процессе полета поддержание орбитальной ориентации космического аппарата (КА) является наиболее распространенной задачей, реализуемой системой управления движением. Характерной особенностью решения задачи стабилизации орбитальной ориентации является предположение о совпадении связанной системы координат с главными осями инерции КА. Однако в процессе длительного полета КА, по мере выработки запасов топлива, может достаточно существенно измениться тензор инерции КА [1], и, как следствие этого, связанная система координат не совпадет с главными осями инерции. Это обстоятельство приведет к ухудшению точности орбитальной ориентации, если не скорректировать закон управления стабилизацией. Данная статья посвящена синтезу аналитического решения задачи стабилизации орбитальной ориентации при несовпадении связанной системы координат с главными осями инерции.

1. Уравнения движения КА

Динамические уравнения углового движения КА при воздействии гравитационного момента и момента управления имеют вид

(1.1)

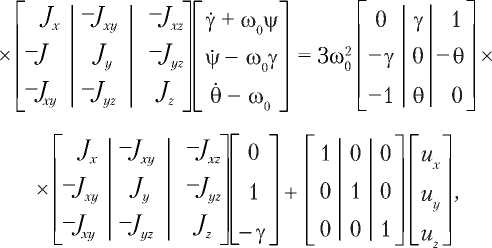
здесь γ, ψ, θ — углы крена, рысканья, тангажа соответственно; u _x , u _y , u _z — управляющие воздействия. Если отбросить слагаемые второго порядка малости, то при условии незначительных угловых скоростей система (1.2) будет выглядеть так:

Ex = A*x + B*u + M*^,

(1.3)

где

E =

e22

e42

e24

елл e46

^e26 0

^e46 0

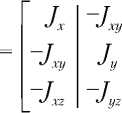
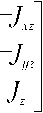
матрица тензора

инерции КА [2];   = i ₂ — единичный вектор

местной вертикали [1]; ω₀ — орбитальная скорость КА на круговой орбите; ω_абс — вектор абсолютной угловой скорости в проекциях на связанный базис; M _упр — управляющий момент. В предположении малых углов отклонения связанного базиса от орбитального вместо (1.1) имеем [2]

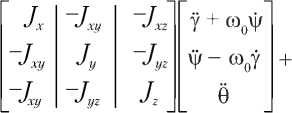
-9 + ю0 О у + о0у

V " «V

-?-«Л

О

(1.2)

e22

e«

M «^^ 46

= - ;e= - J ; e_rr

62 xz¹ 64 yz об

^21 ^®O^Jy J^ ^22 0, Q.^

a„, = -co_n( J + J -J.);             / ; a.„. = 2co / ;

24        O^v^ x ^ y и i 2э          O^xz 26           yz¹

a,, = 4co,/ ; a,,, = co_f( J + J ~J^', a,., = «>“( / -/.);

а,, = 0; а,г = ЗоЗ J ;а = ~2(on J ; 44      ’ 45            yz’ 46           0*^ xz ’ а,. = ~4<У J ; а = ~2соп / ; а = -со^ / ; 61          0*^X2    62          0^ yz 63           yz’

«64= 2юоЛ; «65= 3®о(Л "Л>; «66 = °;

^=U° = a ^ ^)^г=(-4с-к/ to²J Зо^/ У;

• -         ^х ~Х ^у         ^х 0^ yz VW xz ^Ху' ’

х=(х. х„ х., х, х, хЛт; и = (и и

• х. = у; х= у; х = ш; х, = \i/; х, = 0; х_с = 9, где ξ _x , ξ _y , ξ _z — постоянные возмущения, обусловленные линеаризацией системы (1.2). В форме Коши выражение (1.3) будет иметь вид

(1.4)

где A = E ^–1 A* , B = E ^–1 B* , M = E ^–1M * .

Поскольку объект, описываемый уравнением (1.3), подвержен детерминированному внешнему возмущению ξ(t) = const, то для определения управляющего воздействия задачи орбитальной стабилизации воспользуемся методом, изложенным в [3]. Считаем, что нам задан трехмерный вектор регулируемых переменных y = Cx,                (1.5)

где C — матрица регулируемых параметров размером 3×6, такая, что rank

А, В С^ о₃.₃

Требуется найти управление u, при котором установившаяся ошибка по регулируемому вектору удовлетворяла бы условию , а корни характеристического УС1 z^-co уравнения замкнутой системы автоматического регулирования располагались бы заданным образом в плоскости корней.

Для решения задачи введем новые переменные ∆ x = x – x _уст и ∆ u = u – u _уст, где x _уст и u _уст — установившиеся ошибки по векторам состояния и управления соответственно. Поскольку = 0, из уравнения (1.4) следует, что Ax _уст + Bu _уст = –Mξ, а поскольку y _уст = 0, то, согласно тождеству (1.5), Cx _уст = 0. Таким образом, можно записать выражение для объединенного вектора установившихся ошибок

Предположим, что некоторым образом найдено управление ∆u = –K∆x с матрицей регулятора по состоянию K размерности 3×6, обеспечивающее требуемое расположение корней. Тогда, согласно определению переменных ∆x и ∆u, очевидно, что u = –Kx + (Kxуст + uуст). Другими словами, возвращаясь к прежним переменным, с учетом (1.6) можно получить искомое управление и = -Кх- [К,£3]

А, В

С, 0_3х3

м

Оз.з

(1.8)

Символом E _n обозначена единичная матрица порядка n . Отметим, что управление может быть вычислено по формуле (1.8) тогда и только тогда, когда выполняется соотношение (1.5).

Применительно к рассматриваемой задаче матрица регулируемых параметров имеет вид C = [E3, 03×3]. Подставив указанные значения параметров в формулу (1.8) и проведя соответствующие расчеты в пакете символьных вычислений Symbolic Math Toolbox (среда Matlab), окончательно получим тождество u = –Mξ – Kx.             (1.9)

• 2. Аналитическое решение задачи управления

Для поиска аналитического решения управления системой (1.4) воспользуемся методом точного размещения полюсов [3]. Для этого будем использовать линейную многомерную динамическую систему с многими входами и многими выходами ( MIMO — Multi Input Multi Output )

Dx = Ax + Bu ,          (2.1)

где x ∈ R ⁿ — вектор состояния; u ∈ R ^r — вектор входа; R — множество действительных чисел; n >  r; D — символ, обозначающий либо оператор дифференцирования Dx ( t ) = х , либо оператор сдвига Dx ( t ) = x ( t + 1).

Предполагается, что матрица B ∈ R ^{n × r} имеет полный ранг, а матрица A ∈ R ^{n × n} заведомо неустойчива, т.е. множество ее собственных значений ( спектр )

eig(A) = { λi ∈ C: det (λIn – A) = 0}, где In — единичная матрица размера n×n; C — множество комплексных чисел (комплексная плоскость), обязательно включает такие λ i ∈ C, что Re(λ i) > 0 для случая Dx (t) = x и | X J > 1 для случая

Dx ( t ) = x ( t + 1).

Здесь | λ _i | — модуль собственного значения λ _i .

Введем понятие Cstab, которое в дальнейшем, в зависимости от типа изучаемой MIMO-системы (непрерывной или дискретной), будет обозначать соответственно левую полуплоскость C- плоскости C, т.е. Cstob = C-, либо область внутри круга единичного радиуса с центром в начале C, т. е. Cstab = C|х] < 1. Считается, что для MIMO–системы (2.1) существует управление с обратной связью вида u = –Kx, (2.2)

где K е R ^{r x} n — матрица регулятора по состоянию.

Управление системой (2.1) с помощью законов (2.2) является классической задачей, когда необходимо найти такую матрицу K , которая обеспечивает требование на размещение полюсов замкнутой системы (собственных значений матриц A – BK ) в заданных точках C ^stab или в заданной области C ^stab (заданной областью, например, может быть вся левая полуплоскость C ).

Требования на распределение полюсов можно задавать с помощью разложения полинома на множители, например det( V -А + ВК) =

-(х-х^х-х^-кУ

(2.3)

где — заданные значения корней полинома (собственные значения матрицы A – BK ).

Пусть B ^{⊥ T} = null( B ^T ) — ортогональная матрица, удовлетворяющая условиям

B ^⊥ B = 0     ;

( n - r )х r ¹

(2.4)

(2.5)

L-й (конечный) уровень , L = ceil(n/r) – 1,

(2.9)

где ceil(*) — операция округления числа * в сторону большего значения, например, ceil(0,1) = 1, ceil(1,6) = 2, ceil(2,01) = 3 и т.д.

В соответствии с теоремой [4] для MIMO -системы (2.1) матрица K е R ^{r x n} , определяющая регулятор по состоянию, удовлетворяет формулам

(2.10)

(2.11)

(2.12)

(2.13) тогда eig(A – BK) =   eig(Фi – 1).     (2.14)

Из теоремы вытекает следующий алгоритм синтеза регулятора, обеспечивающего заданное размещение полюсов:

• 1)    назначить матрицы A ₀ = A ; B ₀ = B ;

• 2)    вычислить L = ceil( n / r ) – 1;

• 3)    задать матрицы Ф = Ф₀, Ф₁, …, Ф _L та-

• L + I

кие, что   eig(Ф _{i – 1}) — желаемый спектр замк-

• i-    1

нутой системы;

• 4)    рассчитать ортогональный аннулятор = B ^⊥ , а затем матрицы

ArB0LA0Bf;Bx=B^A0B0,..,

A^Bt-A-^-vB^Bt-A-A-v

• 5)    вычислить ортогональный аннулятор , а затем матрицы

• 6)    определить ортогональный аннулятор , а затем матрицы

A_L-rBtA,. 2^^Г₂; B_L__X = b_la₂a_{l 2}b_{l 2};

• 7)    рассчитать ортогональный аннулятор , а затем матрицы

Л ^ ^s, A _tBfi- b_l - Bt ,a_{l t}B_L •

• 8)    последовательно вычислить матрицы

3. Орбитальная стабилизация КА

Kl=B-lAl -ФД-;

b_l1 = ^kl^bLi ⁺ в A A-i ⁼ BlAl-i - ^фь-1^В_ь__г,...;

в; - К, ₊ A + ВГ; К, - B7A, - Ф,В7,...; к к+ 1 к к’ к к к к к' ¹

В; = К₂ВАВ*;К^ =В;А_х - Ф_ХВ;;

В^К^АВ-К-К^ВА-ФД-

Регулятор с матрицей (2.10) обеспечивает выполнение условия (2.14).

Рассмотрим далее применение изложенного в разд. 2 алгоритма синтеза регулятора, обеспечивающего заданное размещение

полюсов применительно к задаче нахождения законов стабилизации орбитальной ориентации КА, которая описывается моделью (1.3). В данном случае имеем

A = KVA* =

'*

гдеQ 0 :

“31

Q. °

Q 0

“23

Q °

U2A

Qm

Q 0

“26

ad

<2°

“б!

й22

о

“42

О я0

“б2

U23

Q?

fl°3

U24

a4A й64

6°	b0	Ь о
21 о	^22 о	23 о
№	b о	ь0
41 Q	42 Q	43 Q
№	Ь 0	b о
61	62	63

-(еЛа.,е/с - аГАелл)

^x 26^х Ал 46     61 AA'

0 fl”5 0 a4°.

й65

^З^зХбб

й31646 1 йзХ44^66^^й ’

- ^^е₂сА^а42^е46  ^aG2^e44^ ^ЗЗ^ЗЗ^бб

- а22е26 + а22е44е66)М

“ -(е2б(й2бе44 ” й4364б) ” ^23^й33^66 й23б46 + й23е44ебб)/й ’

- (е26(а44е46  й64е44)   е24(й44е66

й24^46 + й24е44ебб)/й ’

— (е26(а45е46   а65е44)   е24(а45е66

" °25^е46 ⁺ ^ЛзбйХМ

= ~ (^“жС^/К^/К  62^6,,)  ^/(^/Г^КК х 26 х 46 46     66 44 7     24 х 46 66

й3б^36 + й2бе44ебб)/й ’

“ ^66^24 ” 2е₂₄е₂₆е₄₆ + е₄₄е₂₆ + е₂₂е₄²₆

й26

й46

й66

(3.1)

aG\e\^

a^4^

й63в4б) ~~

ar,6,A ""

64 46 7

«65e46) ~

66 467

- e,,,,e,,e"

22 44 66’

Й11 —  ^Зб^зХзб  йбХз2'  б24Хй21^66  й61б2б'

йзХзб + йзХз3^66-)/й > й42 —  ^46^й23^36  й62е2г)  ^ЗЗ^ЗЗ^бб  й62б2б)

й42626 ' й42622ебб)/й ’

^П43 —  (^Зб^ЗЗ^Зб  ^й63^е2г)  ^ЗЗ^ЗЗ^бб  ^й63^б26^

й33^26 + й33^22^66-1^й > й33 — (е4б(й24б26   й64е2г)   ^ЗЗ^ЗЗ^бб й64б2б)

- «₄₄е²₆ + a_ue₂₂e₆₆)/a^ri;

й35 — (е4б(й25б36   й65бгз)   егз(й35в66 й65б2б)

4:з 26      45 22 66^7/    ’

= -(^ЛйС^Ак - Йййе9з) “ взХ^ЗГ^ЙЙ “ Йййб3й) “

46 х 46 х 26 26     66 22z     24 х 26 66     66 26z й46б26 + й4бе33в6б)/й >

^Й61 ^— (^б4б(^й21^е24   ^й41^бгз)   ^е36^^й31^е44 ^а4\^в24^

й61б24 + й61е22е4з)/й ’ й62 — (е4б(й22в34   й4262з)   ^Зб^ЗЗ^ЗЗ й32б2з)

- а62е|4 + а62е22е44)/а4

й63    ^36^й23^33   й33^33^   ^36^й33^33   й33®23^

<263e24 а61е22е42)/а , й64 —  (е3б(й23е24   й44езг)   е26^а24в44   й33в2з)

й63е23 + аб4е22е44^/а ’ й65 —  (е3б(й25в33   й3562з)   б2б(й35е33   й35б2з)

" й65е23 + й65е22е44)/й";

^й66 ^—  (^е3б(^й26^в33   ^й36⁶3з)    ^е26^^а26^в44   ^й36^б2з)

й66623 + й6бе22езз)/й ’

^21 — (^ЗЗ^бб в4^/а ’ ^22 — (626в36 е23в6б)/йГ я^ - еййе2 + 2e/ce.,/e9K - e,,eL + e„„(e,,err - е2);

1        66 24       46 24 26     44 26     22х 44 66     467’

^23   х^24^46   к26^447/^22’

^42 ” (^е22^б66    ^в26^/^а ’

^43 ~ (е24б26   е22б4б)/й ’ ^61 ~ (е24б46   ^ЗбАз)/*2!’ bL = Ь®; Ь“ = (е е - е- ^/а'1.

62     43’ 63 х 22 44     247/

Размерность объекта управления n = 6, вектора управления r = 3, а количество уровней декомпозиции

L = ceil( n/r ) – 1= 2 – 1 = 1

— два (нулевой и первый).

Будем считать, что заданный характеристический полином замкнутой системы (2.3)

имеет вид det(X/6 - Л + BK) =

= (Х-Х1)...(Х-Х6) = П(Х-Х), где Xi заданы, исходя из определенных требований.

Согласно введенной в разд. 2 многоуровневой декомпозиции нулевой уровень для MIMO -системы с Dx ( t ) = х и матрицами (3.1) имеет вид

A ₀ = A ; B ₀ = B ;              (3.3)

	1	0	0	0	0	0
=	0	0	1	0	0	0
	V0	0	0	0	1	Оу
							(3.4)
	0	е22	0	б24	0	б26
=	0	'Xj	0	е44	0	е46	.
	0	б26	0	е46	0	е66

Нетрудно убедиться, что для матрицы выполняется условие ортогональности (2.5).

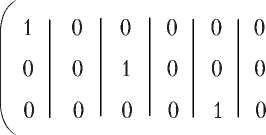
Первый (и конечный) уровень для MIMO- системы с Dx ( t ) = х и матрицами (3.1) выглядит следующим образом:

X

B 1

о? ^а21

о

О-^

о

л0 ^и6\

$о

о

м42

о

й°

“б2

A 1

О

о

G? ^м23

о

U43

о

О?

^63

^0 ^24

Q^

о

а⁰,, 64

д° “25

о

а45

о

= A 0    =

X

О

о

о

о

о

о

о а?

°46

о

о й°

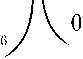
о

=   A 0 B 0

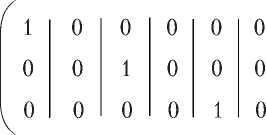
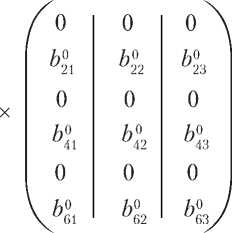
e44e66   е46

ad

e.„.e,R ~ e„,eRR

26 46     24 66

а*

е24б46   е26644

е22

о

о

о

о

о

о

о

о

о

о

;

о

о

о

а'

а\

о е26е

) 0 21 )	1 а®2 0	0 а®з 0	0 “24 1	0 й25 о	0 Q° о
0 41 )	“42 о	“43 о	а44 о	й4°3 о	“4 1
0	(Z®	<7°	а®.		ср
61	62	63	64	65	6
6	^^б		е24е46   е26б44

X а1

а'

^22^66 " в26

ad

^24^26   ^22^46

а*

24 26     22 46

а*1

;

е'14

^26

В^В:^

ем

ем

в46

е46

е.

(3.5)

(3.6)

^22^44   ^24

а*

(3.7)

Зададим матрицы Ф = Ф0 и Ф1 в следую-

щем диагональном виде:

(3.8)

f—X р	622	”3,62,,	e24	X,e26	e26^
32e24	e24	” 32e44	e44	—32646	e46	;
у— ^Зе26	e96	— 33e46	e46	^66	еббЗ
	K =	K 0 = A 0 –		Ф0  =
”3,622	622	—3,e24	e24		e26
~ ^2в24	e24	” ^-2е44	e44	-32e46	e46	X
\  ^F26	626	— З3б46	e46	— З3б66	б6б7

о

где ( , ) — комплексно-сопряженные пары чисел для всех i = 1, 2, 3.

Выполняя вычисления по формулам (2.10) –

(2.13) с учетом матриц (3.3) – (3.8), получим

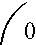
о

X

K ₁ =   A ₁ – Ф 1   =

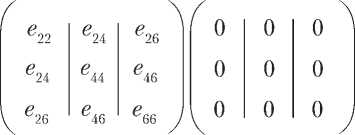
о

о

в22

Ft

е96

(3.9)

о

'2

О

о

'з

е22Х

в X

^24 2

б24

е26

Fi\ ^б44^2 е₄₆Х₃

б44

е46

е263,

^46 2

еббз /

У о ^0

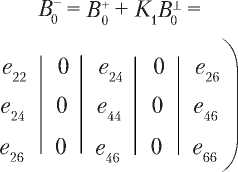
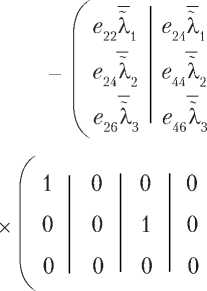
б2б3, в,- К

46 2

е66Х.3 у

О (У о о

1 0 7

е46

е,

X (3.10)

X

где

о

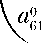
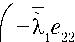
\е2Л

7 £

Fl а

\ Fl

k 11

k ₁₃

– a ₂₁

о о0

о о0

о й63

й44

О й64

О

7° о 7°

О

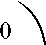
о

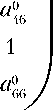
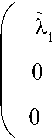
О

к

о

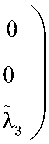
X

— 7/9

У \3 26

e22	”3,e24	e24	“ ^1е26
624	” ^"2e44	«44	— 32e46
e26	— 33646	e46	— З3б66

^32

^13

^23

^33

e 22      ;

(3.11)

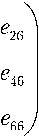
^14

^24

^34

h

^25

^26

^36 j

k ₁₂ = e ₂₂

a ₂₂ + e ₂₂ ;

a ₂₃ – e ₂₄    ; k ₁₄ = e ₂₄   – a ₂₄ + e ₂₄  ;

k ₁₅ = – a ₂₅ – e ₂₆    ; k ₁₆ = e ₂₆ – a ₂₆ + e ₂₆ ;

k ₂₁ = – a ₄₁ – e ₂₄    ; k ₂₂ = e ₂₄   – a ₄₂ + e ₂₄  ;

k ₂₃ = – a ₄₃ – e ₄₄    ;

k ₂₄ = e ₄₄ – a ₄₄ + e ₄₄  ;

(3.12)

k ₂₅ = – a ₄₅ – e ₄₆    ; k ₂₆ = e ₄₆   – a ₄₆ + e ₄₆  ;

k ₃₁ = – a ₆₁ – e ₂₆    ; k ₃₂ = e ₂₆   – a ₆₂ + e ₂₆ ;

k ₃₃ = – a ₆₃ – e ₄₆     ; k ₃₄ = e ₄₆   – a ₆₄ + e ₄₆  ;

k ₃₅ = – a ₆₅ – e ₆₆    ; k ₃₆ = e ₆₆   – a ₆₆ + e ₆₆  .

Приведенные аналитические выражения (3.12), собственно, и определяют аналитическое решение задачи орбитальной стабилизации.

Получим далее значения коэффициентов в матрицах стабилизирующих регуляторов орбитальной ориентации в случае, когда характеристический полином (2.3) представляет собой полином Баттерворта 6-го порядка, имеющий вид

X⁶ + 3,8637X 5 + 7,4641X 4 +     (3 13)

+ 9,1416X 3 + 7,4641X 2 + 3,8637X +1. ^{1 .}

Корни полинома (3.13) равны

= – 0,2588 + j 0,9659;  = – 0,2588 – j 0,9659;

= – 0,9659 + j 0,2588;

^{,            ,}                (3.14)

= – 0,9659 – j 0,2588;

= – 0,7071 + j 0,7071;   = – 0,7071 – j 0,7071.

Подстановка корней (3.14) в матрицу (3.11) дает следующие значения элементов матрицы коэффициентов регулятора

k 11 =	– a 21	e 22; k 12 = –	0,5176 e 22	– a 22;
k 13 =	– a 23	– e 24; k 14 = –	0,5176 e 24	– a 24 ;
k 15 =	– a 25	– e 26; k 16 = –	0,5176 e 26	– a 26 ;
k 21 =	– a 41	e 24; k 22 = –	1,9318 e 24	– a 42;
		k 23 = – a 43 –	e 44;	(3.15)
	k 24	= – 1,9318 e	44 – a 44;
k 25 =	– a 45	– e 46; k 26 = –	1,9318 e 46	– a 46;
k 31 =	– a 61	– e 26; k 32 = –	1,4143 e 26	– a 62 ;
k 33 =	– a 63	– e 46; k 34 = –	1,4143 e 46	– a 64 ;
k 35 =	– a 65	– e 66; k 36 = –	1,4143 e 66	– a 66.

Варьируя индексы в (3.14), можно полу- чить эквивалентные, в смысле удовлетворения характеристического полинома (3.12), значения элементов матрицы коэффициентов регулятора. В качестве численного примера рассмотрим только задачу стабилизации орбитальной ориентации КА.

• 4.    Численный пример

Пусть начальный вектор состояния контура ориентации КА имеет следующие значения: x1 = x3 = x5 = 10°; x2 = x4 = x6 = 0. Массоинерционные характеристики КА и пара- метр круговой орбиты равны: Jx = 4 600 кгм2; Jy = 25 000 кгм2; Jz = 24 000 кгм2; Jxy = 840 кгм2; Jxz = 850 кгм2; Jyz = 850 кгм2; rn0 ^= 0,001 c-1. Для этих исходных данных проведем оценку точности орбитальной стабилизации КА в случае, когда значения элементов матрицы коэффициентов регулятора определяются выражением (3.15) и применяя решение, представленное в [4]. Результаты моделирования показали, что полученное в данной статье решение, определяемое (3.15), обеспечивает точность орбитальной ориентации на 0,11° выше, чем изложенное в [4].

Заключение

В статье рассмотрена задача орбитальной стабилизации КА при несовпадении связанной системы координат с главными осями инерции КА. С помощью метода точного размещения полюсов осуществлен синтез законов во всех каналах управления и, соответственно, получено аналитическое решение при полной матрице тензора инерции. В отличие от [4], найденное в данной работе решение задачи орбитальной стабилизации КА является универсальным и, соответственно, пригодно для любого вида матрицы тензора инерции, обеспечивает более точную орбитальную стабилизацию.