Стабилизация программных движений большой динамической системы с ограничениями на векторы координат и управлений

Задачи стабилизации положения равновесия и стабилизации программных движений выделены в отдельные классы задач управления [1]. Указанное разделение классов определяет современные прикладные задачи синтеза динамических систем, таких как управление летательными аппаратами [2; 3], объектами водного транспорта [4–6] и др. [7–9]. Для решения задач стабилизации положения равновесия и программных движений используются методы бэкстеппинга [10–12], обратных задач динамики [13] и др. [14; 15].

Ефремов Артем Александрович

В работе для стабилизации программных движений большой динамической системы применяются проекционно-операторные методы математического программирования [16–18]. Указанные методы отображают параметры функционала и ограничений задач математического программирования в допустимые или оптимальные решения.

Оператор решения задач стабилизации программных движений

Большая динамическая система, образованная из s подсистем, определена блочно-диа- гональным оператором вида        ˆˆ

^X k + 1 = ^{H ( X} k ^{) + FU} k ,

ˆ

Y k = C y X k , X k 0 = X o

В блочно-диагональном операторе (1) введены следующие обозначения:

• •    блочный вектор фазовых координат динамической системы, состоящий из фазовых

координат s подсистем, с блоками размера n : X _k = ^[ x k ,—, x k ,—, x k J e R s ^x n ;

• •    блочный вектор управляющих воздействий динамической системы с блоками разме-

• U 1 i s T     s x m k    = [uk,''',uk,''',ukJ eR ; •    блочный вектор выходных координат динамической системы с блоками размера l: Yk   Гуk ’"•’yk,''', yk ]T e Rsxl; •    блочный нелинейный вектор динамической системы, состоящей из s подсистем, с блоками размера n: IH (xk ) = [H1 (xk) ,'„, Hi (xk) ,'„, Hs (xk )J e R(sxn), Hi (xk )e Rn; •    блочно-диагональная матрица управлений динамической системы с блоками размера (n x m): F = diag {F1, '•',

F i ,'", F s } e R ⁽ s ^x n ^)x( s ^x m ) , F i e R n ^x m ;

• •    блочно-диагональная матрица выходов динамической системы с блоками размера

( l x n ): C Y = diag { c ‘ ,'•', c y c y } e R ⁽ s ^x l ^)x( s ^{x n} ) , c y e R l ^x n •

Блочно-диагональный оператор (1) включает нелинейные стационарные управляе- мые по Н.Н. Петрову [19] разностные операторы:

^x k + 1 = ^H i ( ^x k ) ^{+ F} i u k , ^y k = ^C y ^x k , ^x k 0 = ^x 0 '

n x m

Векторы и матрицы в (2) имеют вид x k _{+ 1} e R n , y k e R l , u k e R m , F i e R‘ C y e R l ^x n , H i ( x k ) e R n '

Стабилизация программных движений большой динамической системы ...

Оператор стабилизации программных движений большой динамической системы с ограниченными векторами координат и управлений

Утверждение 1. Блочно-диагональный разностный оператор (2) определяет оператор вида

AZ k = b k ,                                     (3)

где векторы состояний-управлений для s нелинейных подсистем заданы равенствами ^Z k =[ ^z k ,..., z k ,..., ^z k ] , ^z k =[ x k +i| u k ] , A = diag { A i ,..., A i ,..., A s } , A i = [ ^E n x n |F i ]^T , b k =[ b k ,..., b k ,..., b k ] ^T , b k = H ( x k ) .

Доказательство. Оператор (2) представлен векторно-матричным нелинейным уравнением

	_ E n X n    ...     0	...       0 I		[ X1 ,1 x k + 1		" F    ... 0	... 0 I		1 1
F =	...        ...        ...        ...        ... 0     ...    E n X n   ...     0		X	... x k + i		......... 0 ...    F i	...... ... 0	X	... u k
	...        ...        ...        ...        ... [ 0     ...     0     ... E n X n _			... [ x k + i J		......... _ 0 ... 0	...... ...    F s _		... [ u k ]
		’ H i ( x k ) ...		0.		..          0 I
= =		...           ... 0        ...	...            . H ( x k )			..           ... ..        0	■
		...           ... [      0         ...		...            . 0.		..           ... .. H s ( x k )

Преобразования векторно-матричного уравнения определяют равенство

E n x n x k +1	- F 1 u k '		■ H, ( x k) ...
... E n X n x k + 1	- Fu iki	=	H i ( x k )
... E n X n x k + 1	- F S u k J		... h s ( x k )

После выделения обобщенных векторов фазовых координат и управлений zk = I xk+1 uk I левая нелинейная часть оператора принимает вид

[ E n х n l- F i ]

^x k + 1 u 1 _k

,...,

[ E n . n HF ] ’“

...

u _k

[ E n X n |- F s ]

T xk+1

^u k _

H 1 ( x k )

...

H( x k)

H S ( x k )

Выполнив замену переменных и выделив блочно-диагональную матрицу Â и блочный вектор состояний-управлений Z _k, можно получить равенство

AZk = b k, где матрица      A = diag{A1,...,A;-,...,As}, Ai =[Enxn|FiJT, bk =^bk,...,bk ,...,bkJ , bk = H ( x k )’ Z k =[z k ’...’z k ’...’z k J ’ z k = [xk+11 uk J ■

Утверждение 1 доказано.

Оператор (3) определяет условие-равенство в задаче стабилизации положения равновесия или стабилизации программных движений [20] большой динамической системы. Постановка указанных задач имеет вид: вычислить обобщенный вектор «состояний-управлений» евклидова конечномерного пространства R ^s×(n+m)

z k = arg min { ф ( Z k ) = | |Z k 1 2 | A Z k = b k , [ Z k — C k ] ^T [ Z k — C k J^ r 2 } e R s⁴n ⁺ m ) , (4) где C k =[ C 1 k ,..., C ik ,—, C sk J T — блочный вектор допустимых программных движений фазовых координат и управлений, C _ik = ^[ C x _k | C u _k J e R n ⁺ m , r e R .

Счетное число решений задач конечномерного математического программирования (4) определено проекционным оператором, синтезированным в [21]:

Z k ( ° 1 , ° 2 , 0 ) = 0 Z k ( ° 1 ) + ( E - 0 ) Z k ( ° 2 ) ,

Zk (°j) = P+bk + °P0Ck, J = 1,2, где                                                                            Z k =[ X k+1 |U k ]T, aik = (bk )T (p; )T Cik - (bk )T (P+ )T P+bk + Cik^bk + CTkPC - CTkCik + r2, gik = C kPTCik , °1 k = diag ° >•••> °ik >•••> °sk},     °2 k = diag {° 2 k >•••> °2 k >•••> ° 2k},

° k = ^{1 -} fi kadgi , ° 2k = ^{1 +} 4 kkgSi ’ ^ё = diag { в 1 ^,... A ^,...^, в s } , J’ ⁺ = diag { P 1 + ^,...^,P+^,...^{, P} s ⁺} ,

P i⁺ = A T ( A i A T ) ^{- 1} , p^{1 0} = diag { P 1⁰ ,..., P i ⁰,..., P f } , P° = E „ - A T ( A i -A T ) " * A _f , 0 e [ 0;1 ] .

Вектор «состояний-управлений» (5) позволяет синтезировать оператор стабилизации программных движений большой динамической системы с ограниченными векторами координат состояний и управлений

X k + 1 = H ( X k ) + Y FU k ( X k , ° 1 , ° 2 , 0 ) •                          (6)

В (6) вектор локально допустимого управления имеет вид

Uk = T„Zk = T„ (0 P+bk + °1P0Ck + (E - 0) (P+bk + °2 P0Ck)), где T„ = diag{TU,...,T T„s}, T =[0иxn|EиxиJT – блочно-диагональная матрица, «фильтрующая» векторы управлений uik i-х подсистем.

Диагональная матрица параметров обратной связи

Y = diag {/1,..., Yi,:; Ys}, где γi – параметр обратной связи подсистемы с номером i, вычисляемый на основе принципа сжимающих отображений [21] как

Стабилизация программных движений большой динамической системы ...

н<(нНт1ЛН+^^

4MdHM/Hc-i2)4h4x^^^^^

Выполнение неравенства (7) является достаточным условием устойчивости подсистемы в операторе (6).

Вычислительный эксперимент

В качестве примера рассмотрено электроэнергетическое объединение, состоящее из трех электроэнергетических систем, подключенных к шине бесконечной мощности линиями электропередач (см. Рисунок 1).

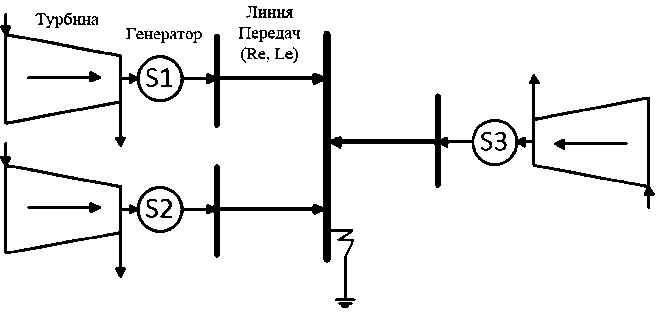
Рисунок 1. Структура электроэнергетического объединения Источник: схема выполнена автором.

Электромеханические процессы в i -й электроэнергетической системе описываются уравнениями турбины

2J№ dai

~7~ = TMxi - Tei - Dai,     = ®r pi dtdt

Уравнения линии передачи, связывающей i-ю электроэнергетическую систему и шину бесконечной мощности, имеют вид vdl = 0,06idl + 0,011idi -0,011aliql + 10cos(p); vdl = 0,06 iqi + 0,011iq 1 + 0,011a idl + 10sin (p).

Электромагнитные процессы в электроэнергетическом объединении описывает блоч- но-диагональный оператор

Г хП A1 ( х1 ) Г B 05x3 05x3 Г u11 t х2 = A2(х2) + 05x3 B2 05x3 u2 ,                          (10) . х3. .A3 (х3 )_ .05x3 05x3 B3 . .U3 . где xi = .id i‘q if ilqd i'rq J , ui = .ud u'q uf J - векторы координат состояний и управлений.

Для вычисления параметров, входящих в блочно-диагональный оператор (10) векто- ров и матриц, использованы технические данные синхронных турбогенераторов ТВВ-320-2 (S1 и S2) и ТВВ-500-2 (S3) [22]:

	"- 3,05 i 1,2 + 9,56 ® i ],2 dq	- 0,22 i f 2	- 2,8 i rd2 - 5,78 . q2
	6,18<'Л 2 - 1,95 i 1,2 dq	+ 3,7.2 + 3,7. d 2 -5,99 i r q 2
A 1,2 ( x 1,2 ) =	- 0,98 1,2 + 3,M 2" dq	-1,92 i J2 + 5,32 i r d 2 - 1,85 ® i rq2
	- 3,59 1;2 + 11,35 ® i 1,2 + 1,55 i 1;2 dqf		- 10 i rd 2 - 6,79. q2
	8,64.. - 2,73 iq’2	+ 5,18 ® ]’2	+ 5,18 ® i rd 2 - 10 i rq2

A 3 ( ^x 3 ) =

- 3,59 i ³ _d + 10,58 ® q - 0,08 i 3 - 1,03 i 3 _d - 4,13 ® i 3 _q - 6,78 . 3 - 2,3 i q + 2, 65 & i f + 2, 65._d - 2,44 i rq - 1,39 i d + 4, 09. - 1,58 i f + 3,61 i 3 _d - 1, 6._q - 6,93 i d + 20,44 ® i q + 1,38 i 3 - 6,25 i 3 _d - 7, 98._q - 14, 79. - 5,01 i q + 5, 78. + 5, 78 ® i^ - 6, 25i r _q

B 1,2 =

- 5,8	0	0,22 "		"- 4,1	0	0,08 '
0	- 3,7	0		0	- 2,6	0
- 1,9	0	1,9	, B 3 =	- 1,6	0	1,6
- 6,8	0	- 1,6		- 8	0	- 1,4
0	- 5,2	0 ]		_ 0	- 5,8	0 ]

Преобразование модели электроэнергетического объединения (8)–(10) к дискретной форме выполнено в среде динамического моделирования SimInTech [23].

Для динамической системы (6) компоненты диагональной матрицы «допустимости» θ: θ1, θ2 и θ3 подобраны экспериментально и равны 0,505. Параметр r = 1. Блочный вектор допустимых программных движений-управлений, задающий ограничения на векторы ко- ординат и управлений, задан в виде

C = [ C 1| C ₂| C ₃ ] ^T € R ³⁰ , C 1 = [ C |C ] = [ 0,04 0,04 0,03 0 0|0 0 0,3 0 0 ] T e R ¹⁰ , C 2,3 = [ c 2,31 C 2 ,3 ] = [ 0,06 0,06 0,03 0 0|0 0 0,3 0 0 ] T e R ¹⁰ .

Графики изменения мощности турбин (8) учитывают динамику внешней мощности и нагрузку, определяемую процессами сети и первичным регулятором скорости вращения, показаны на Рисунке 2.

С учетом изменения нагрузки динамика относительных частот ωi электроэнергетических систем, входящих в электроэнергетическое объединение, приведена на Рисунке 3.

Динамика ограниченных вектором допустимых программных движений C _x токов электроэнергетических систем, приведена на Рисунке 4.

Синтезированные локально допустимые управляющие воздействия u _f, ограниченные вектором допустимых программных управлений С _u, показаны на Рисунке 5.

Вычислительные эксперименты демонстрируют возможность стабилизации программных движений большой динамической системы с ограниченными координатами состояний и управлениями.

Стабилизация программных движений большой динамической системы ...

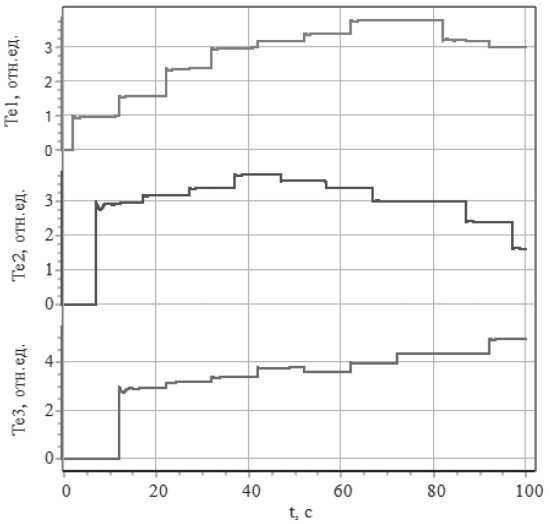
Рисунок 2. Графики изменения мощности турбин Источник: здесь и далее графики выполнены автором.

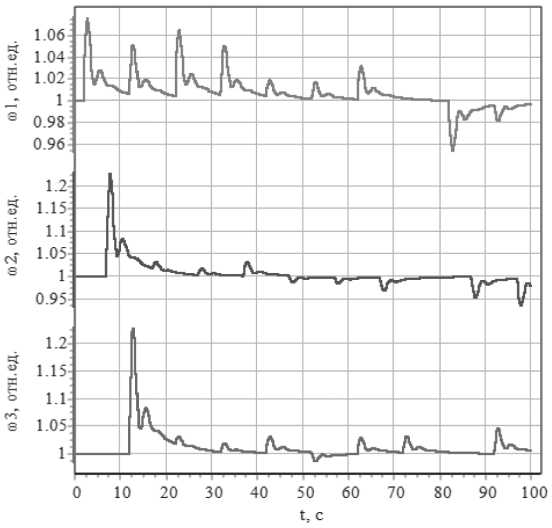
Рисунок 3. Динамика относительных частот ω _i

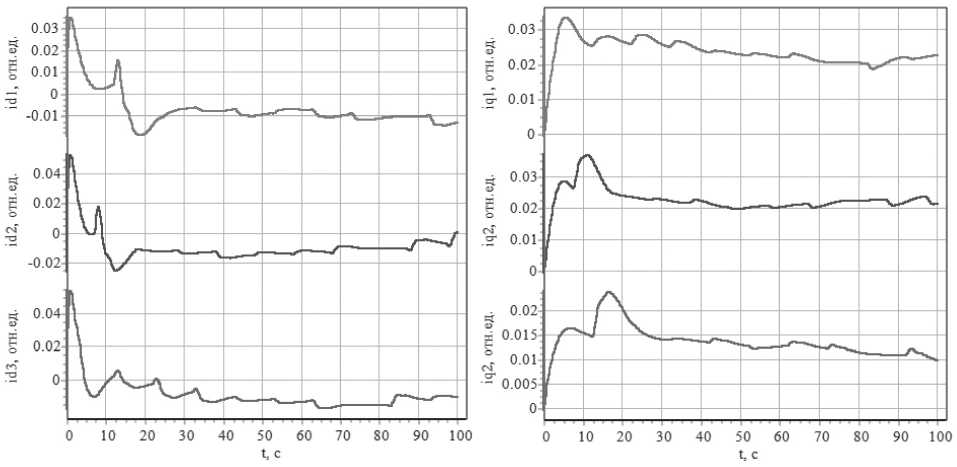
Рисунок 4. Динамика ограниченных токов электроэнергетических систем

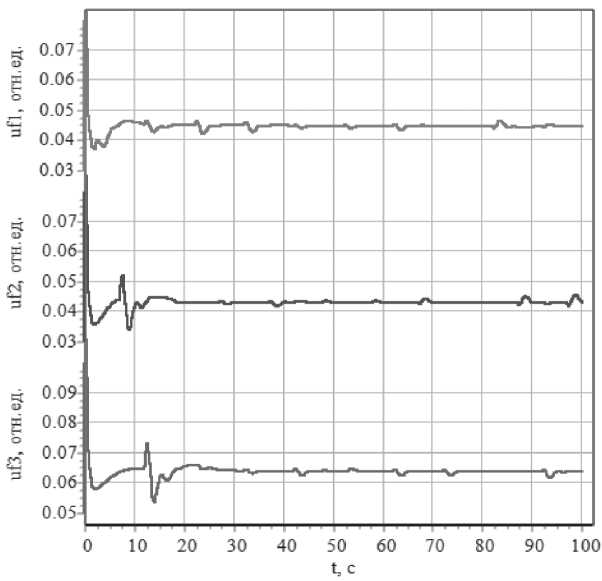
Рисунок 5. Ограниченные напряжения обмоток возбуждения u _f

Выводы

В работе синтезирован проекционный оператор большой динамической системы, состоящей из s подсистем. Указанный оператор применим для решения задач стабилизации программных движений или положения равновесия с ограничениями-неравенствами на обобщенный вектор «состояний-управлений».

Вычислительный эксперимент продемонстрировал возможность применения проекционного оператора для стабилизации программных движений динамической системы с ограничениями на координаты состояний и управлений.

Стабилизация программных движений большой динамической системы ...