Стабилизация углового положения ракеты в вертикальной плоскости при определении оптимальных коэффициентов автопилота с использованием программных средств среды “Matlab”

Повышение боевых возможностей авиацион- ной противокорабельной ракеты (АПКР) связано как с совершенствованием конструкции или алгоритмов работы ее отдельных органов, так и с совершенствованием методов ее применения. В настоящее время использование ее реальных прототипов для исследования невыгодно с экономической точки зрения, поэтому и в замене идут методы моделирования технических систем. Одним из ведущих методов моделирования является математическое моделирование с использованием компьютерных и программных средств. В статье рассмотрен метод получения коэффициентов автопилота контура стабилизации угла тангажа, позволяющий иметь показатели качества пере- ходного процесса, удовлетворяющие реальной ракете при некоторых фиксированных условиях боевого применения и для их использования в дальнейшем при исследовании.

1. Определение передаточных функцийконтура управления ракеты

В качестве прототипа выбрана авиационная противокорабельная ракета (АПКР) «Гарпун» (Harpoon) [1]. При определении АДХ используется методика, основанная на обобщении теоретических и экспериментальных исследований [2; 3]. Расчёт аэродинамических коэффициентов выполнен для числа Маха М = 0,85. Получены следующие значения аэродинамических коэффициентов:

Cx 0 = 0,49, c “ = 0,366' S¹ = 0'1'

to

m ^a = - 0,056, m ° 2 =- 0,03, m z = - 1

z  zz

Точность полученных коэффициентов вполне достаточна для проведения исследований на ранних этапах разработки при постановке задач, сравнительном анализе схем, при исследовании чувствительности аэродинамики ракеты к пара-

ВЕСТНИК 2017

метрам и конструкторским решениям.

Система уравнений движения ракеты суще- ственно упрощается, если удается разделить ее на две подсистемы меньшего порядка, чем исходная. Первая система описывает движение ракеты в вертикальной плоскости, вторая – движение ракеты в горизонтальной плоскости и движение крена.

Задачи поиска оптимального управления ракеты решаются при помощи программной оптимизации линейной модели [4; 5].

Запишем уравнения продольного движения ракеты:

dV m — = R cos a - G sin 0 - X;

dt

d 0

mV --= R sin a - G cos 0 + Y ;

dt d to.              1             2

I — = M +—m psV1;

z 1 dt          Rz 1 2 z 1

d9

= ^to z 1 ;

dt dx0 = V cos 0;

dt

-0^ = V sin 0 ;

dt sin 0 * sin 9 - a cos 9.

Здесь m – масса ракеты, V – скорость центра массы ракеты, R – сила тяги двигателя, G – сила тяжести, X , Y – проекции аэродинамической силы на оси скоростной системы координат (СК), M_Rz – проекция момента тяги на ось z , связанной СК, 1

M = m o sV ² 1 — проекция аэродинамиче- Az ₁     2 z 1

ского момента на ось z , связанной СК, 0 - угол возвышения, J_z – момент инерции ракеты относительно оси z , связанной СК, ^to _z 1 - проекция вектора угловой скорости ракеты на ось z , связанной СК, 9 - угол тангажа, x ₀ , y ₀ , z ₀ - координаты центра масс ракеты в стартовой СК.

Масса m и момент инерции J _z при работающем двигателе являются переменными величинами, закон изменения которых определяется известными функциями времени.

Последнее уравнение системы (1) после несложных преобразований можно писать в виде 0 * 9 - a . В уравнения (1) параметры бокового движения не входят, система может быть решена независимо от остальных уравнений движения ракеты.

Проведём линеаризацию уравнений движения ракеты. Пусть невозмущённое движение представляет собой участок движения АПКР на маршевом участке типовой траектории. В результате уравнения продольного движения ракеты в вариациях запишутся в виде:

d Δ V dt

+ а 00 А V + а ₀₂ А а + а 04 ^0 = - а ₀₃ ^5 в + a ₀₅ X в ;

d Δ ω            d Δ α

а А V +    z1 + а Аю , + а'      + а Аа =

10                           11      z 1       12                12

dt                   dt dΔδв

= - ^а‘ 3 ”7    ^а 13 ^А ^ в ^{+ а} 15 ^M z 1 в ;

dt а 40 А V + а 42Аа + а 44 А9 - dΔθ dt

^а 43 ^А^ в ^{+ а} 45 Y e ;

dА^-Ат, = 0; Аа + А9-А9 = 0;

di          ^{z 1}

d Δ x ₀ dt

+ а ₅₀ А V + а 54 А9 = 0;

y0 + а60А V + а64А9 = 0. dt

Коэффициенты aij называют динамическими коэффициентами. Для расчета динамических коэффициентов выбранной АПКР используем прием «замораживания» коэффициентов, ког-

да соблюдается условие, что превосходит 20%.

j t ) ^{- a} j ( t k ) не

a_ij ( t_k )

w » ( p ) =    2„ / ^a 1^{3 a} L  . —n.⁽³⁾

p | p ^{+ ( a} 11 ^{+ a} 42 ) p ^{+ ( a} 12 ^{+ a} 42 ^a 11 ) I

При решении задачи стабилизации углового положения будем использовать упрощенные передаточные функции. При их выводе используем ряд допущений: не учитываются вариации скорости, не учитываются влияния силы тяжести и аэродинамического момента от запаздывания скоса потока. В уравнениях это соответствует a ₄₄ = 0, a ‘ 2 = 0. Не будем учитывать коэффициенты a ₁₅ и a ₄₅. Также будем считать, что подъемная сила в основном определяется углом атаки и слабо зависит от угла 5 _В , т.е. принимаем а ₄₃ = 0. Кроме того, можно также не рассматривать кинематические уравнения, описывающие изменение A x ₀ и A у ₀ , так как эти вариации не входят в остальные уравнения.

В результате сделанных упрощений получим систему:

Введем обозначения:

Kc =   1^ 42   = 0,013 - коэффициент усиле- a12 + a11 • a 42

ния;

Tc = I ^^ = 1,078 - постоянная времени; V ^a 12 ^{+ a} 11 • ^a 42

T_{c 1} = ¹ = 41 – скоростная постоянная времени; ^a 42

^ c = — ^{a 42} + ^a ,, — = 0,156 — коэффициент демп-²V ^a 12 ^{+ a} 11 • ^a 42

d Aro Z

dt

dAQ dt dAS

= -a11AroZ - a12Aa - a13A5B;

- a42Aa = 0;

-г-=^M^ ;

dt

AS-AQ = Aa.

Коэффициенты выражаются через аэродинамические и инерционные характеристики ракеты следующим образом:

a ii =

m ^ω z 1 ^z ρ VSl ² 2 J z 1

= 0,265;

a 12

m ^α z 1 ρ SV ² l 2 J z 1

= 0,854;

^a 13

-

S b  2„             R + - CoSV 2

m^{z 1 P} V Sl = 0,458; a₄₂ =---- ²--------- = 0,024.

2 J 1               ⁴² mV

Найдем передаточные функции ракеты для параметров A S , A a , A Q по отношению к A5 _B . Для этого запишем систему (2) в преобразованном по Лапласу виде:

( p² + a₁₁ p ) A S ( p ) + a ₁₂ A a ( p ) = - a₁₃ A5 _B ( p );

p A Q ( p ) - a ₄₂ A a ( p ) = 0;

A S ( p ) - A a ( p ) - A Q ( p ) = 0.

Решая эту систему, найдем искомые переменные в зависимости от AS _B ( p ). Искомые передаточные функции:

W (nA- __________ - ^{а гз( a} 42 ⁺ p ) __________■

W S5 ^{( p} ) =       2                                  ;

p ^ p + ( a_xx + a ₄₂) p + ( a ₁₂ + а₄₂а , Jj

фирования.

Запишем полученные выражения, введя передаточные функции типовых звеньев. С учетом полученных коэффициентов передаточные функции можно представить в виде:

W " ( p ) =

W as ( p ) =

W qs ( p ) =

k c ( T _cp + 1)    .

T² p ² + 2 ^ _cT_cp + 1; T C 1 C

T C p ² + 2 ^ c T c p + 1 ’ ^kC

p (T C p ² + 2 < _cT_cp + 1)

.

2. Моделирование контура стабилизации угла тангажа с помощью пакета программных средств matlab/Simulink

Используя полученные передаточные функции, представим систему стабилизации угла тангажа в виде структурной схемы с типовыми звеньями (см. рис. 1).

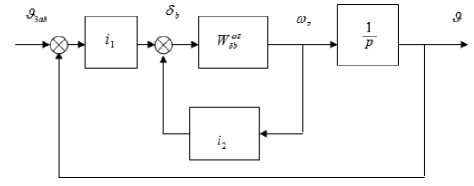
Рис. 1. Структурная схема системы стабилизации угла тангажа

Для расчета переходной характеристики системы составим модель работы системы в математическом пакете matlab/Simulink [6] (см. рис. 4).

При коэффициентах автопилота i 1 = 1 и i 2 = 1, полученная переходная характеристика указана на рис. 2.

ВЕСТНИК 2017

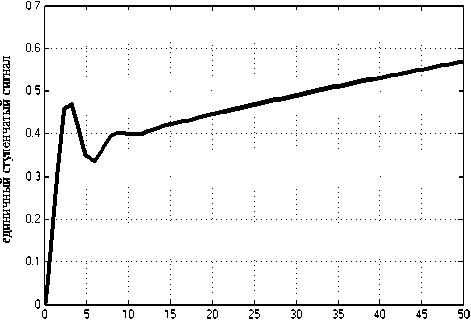
время,с

Рис. 2. Переходная характеристика угла тангажа при коэффициентах автопилота i 1 = 1 и i 2 = 1

ВЕСТНИК 2017

Временем регулирования t_p называется минимальное время, по истечении которого отклонение выходной величины от установившегося значения h _∞ ( t ) не превышает некоторой заданной величины Δ .

Если принять Δ= 0,05 ⋅ h _∞ ( t ) = 0,05 , то из графика переходного процесса время регулирования системы t_p > 50 с.

Перерегулирование определяют следующим h -h образом [1]: σ = m ∞ ⋅100%, где hm – макси-h∞ мальное значение переходной функции. В нашем случаеσ = 0% .

Полученный переходный процесс имеет большое время регулирования.

• 3 . Подбор оптимальных коэффициентов автопилота

Подбор коэффициентов автопилота произведем при помощи встроенных возможностей математического пакета Matlab/Simulink блока библиотеки Simulink Signal Constraint (см. рис. 4).

Подберем коэффициенты автопилота i 1 = 50 и i 2 = 30 вручную таким образом, чтобы уменьшить время регулирования (см. рис. 3).

Полученный переходный процесс апериодический (не колебательный). Из графика переходного процесса оценим время регулирования системы t = 2,22 с. Перерегулирование σ = 0% . ^p

Показатели качества процесса хорошие, но при этом переходный процесс – не оптимальный. Используем данные коэффициенты автопилота i 1 = 50 и i 2 = 30 в качестве начальных приближений для поиска оптимальных коэффициентов обратной связи.

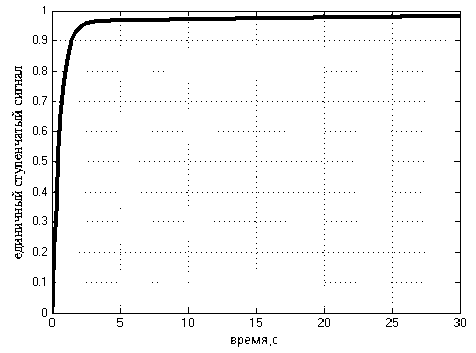
Рис. 3. Переходная характеристика угла тангажа при коэффициентах автопилота i 1 = 50 и i 2 = 30

Блок Signal Constraint позволяет проводить подбор и оптимизацию коэффициентов динамической системы, предъявляя необходимые требования к получаемым переходным процессам на основе методов оптимизации функции нескольких переменных.

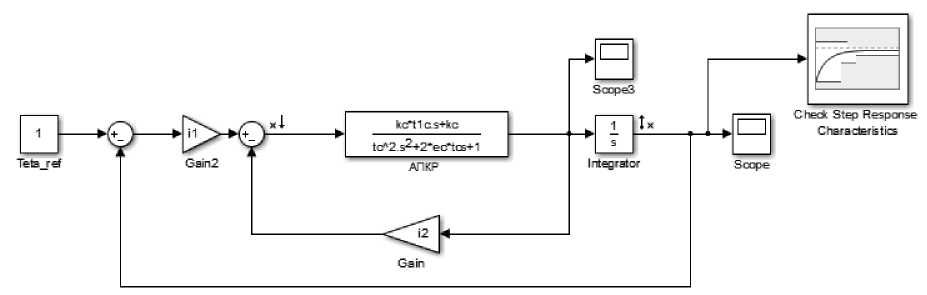
Рис. 4. Модель для подбора оптимальных коэффициентов системы стабилизации угла тангажа

Сначала необходимо произвести следующие настройки:

• –    задать область допустимых значений характеристик переходных процессов;

• –    задать начальные приближения коэффициентов системы управления, возможно задание области допустимых значений каждого из коэффициентов;

• –    задать метод и шаг интегрирования;

• –    выбрать метод подбора коэффициентов (в данном случае использовался градиентный метод минимизации невязок) и максимально допустимое число итераций.

После выполненных операций коэффициенты, удовлетворяющие области допустимых значений характеристик переходных процессов, подбираются автоматически. В нашем случае полученные коэффициенты i 1 = 167,23 и i 2 = 29,849.

Нужно учитывать, что многие методы подбора коэффициентов очень чувствительны к начальному приближению. При оптимальных коэффициентах автопилота переходный процесс угла тангажа выглядит, как на рис. 5.

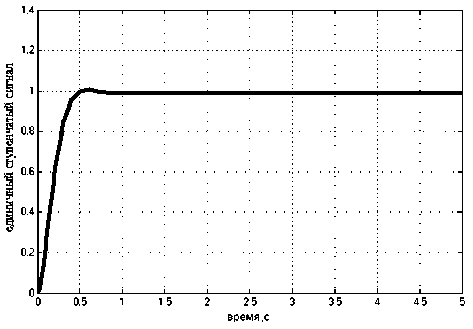
Рис. 5. Переходная характеристика угла тангажа при оптимальных коэффициентах автопилота i 1 = 167,23 и i 2 = 29,849

Оценим прямые показатели качества системы. Процесс астатический, но за время 5 секунд ошибка регулирования составляет е = 0,009, откуда можно сделать вывод, что даже при заданном угле тангажа Э зад = 90 ° ошибка регулирования составит не более е = 0,81 градус. Время регулирования системы t_p = 0,4 с. Перерегулирование _{σ =} ^{1.0056 - 1} _{⋅ 100% = 0 56%}. Переходная ха- 1

рактеристика угловой скорости ω _z представлена на рис. 6.

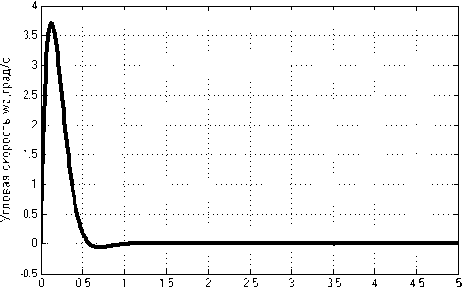
время.с

Рис. 6. Переходная характеристика угловой скорости ω _z при оптимальных коэффициентах автопилота i 1 = 167,23 и i 2 = 29,849

Полученная переходная характеристика – малоколебательная, с малым перерегулированием, но достаточно большим временем регулирования. Поэтому возьмём показатели качества системы с полученными коэффициентами автопилота i 1 = 167,23 и i 2 = 29,849. Откуда закон управления принимаем:

5В = i1 • (^rad — ^ — i2 • toZ =                   (5)

= 167.23 • (^ - ^) - 29.849 • ^Z, где ϑзад – заданное значение.

Выводы

Таким образом, рассчитаны основные массогабаритные и аэродинамические характеристики выбранного в качестве прототипа АПКР.

Определены передаточные функции контура управления ракеты. Предложен вариант контура стабилизации угла тангажа. При помощи программных средств математического пакета matlab/Simulink найдены оптимальные коэффициенты автопилота, при котором переходный процесс угла тангажа имеет удовлетворяющие показатели качества (небольшое время регулирования и перерегулирование) управления ракетой. Это может быть использовано в дальнейшем для исследования процесса управления ракеты .