Стационарная модель переноса ионов соли в двумерном электродиализном канале обессоливания в гальваностатическом режиме
Автор: Узденова А.М., Уртенов М.Х.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 4 т.18, 2018 года.
Бесплатный доступ
Введение. Статья посвящена теоретическому описанию процесса переноса ионов в мембранных системах в гальваностатическом режиме. В качестве мембранной системы рассматривается канал обессоливания электродиализного аппарата. Цели работы: создание и верификация двумерной математической модели стационарного переноса ионов соли в канале обессоливания электродиализного аппарата для гальваностатического режима.Материалы и методы. Предложена новая модель переноса ионов. Она основана на системе уравнений Нернста — Планка — Пуассона для электрического потенциала и на уравнении для функции электрического тока. Получено численное решение краевой задачи модели методом конечных элементов с помощью программного пакета Comsol Multiphysics.Результаты исследования. Разработанная математическая модель позволяет описать стационарный перенос ионов бинарной соли в канале обессоливания электродиализного аппарата. При этом учитываются нарушение электронейтральности раствора и формирование расширенной области пространственного заряда при сверхпредельных токах в гальваностатическом режиме...
Перенос ионов, ионообменная мембрана, мембранная система, гальваностатический режим, математическая модель, уравнения нернста - планка - пуассона, расширенная область пространственного заряда
Короткий адрес: https://sciup.org/142217057
IDR: 142217057 | DOI: 10.23947/1992-5980-2018-18-4-426-437
Текст научной статьи Стационарная модель переноса ионов соли в двумерном электродиализном канале обессоливания в гальваностатическом режиме
Введение. Мембранные системы составляют основу электродиализных аппаратов, нано- и микрофлю-идных устройств, которые применяются при очистке воды, переработке сельскохозяйственной продукции (молока, вина и т. д.), выполнении химических анализов и в других сферах деятельности [1–4]. В многочисленных математических моделях процессов массопереноса в мембранных системах для потенциостатического или по-тенциодинамического режимов электрический режим задается как скачок потенциала между двумя эквипотенциальными плоскостями, параллельными мембранам. Подробный обзор работ, посвященных моделированию для потенциостатического режима, представлен в [5–7].
В то же время в практике электродиализа, электрохимической характеризации мембран (хронопотенциометрия, импедансометрия и др.) часто используется гальваностатический режим, при котором на межфазной границе поддерживается постоянная средняя плотность тока. Об этом режиме собран огромный объем экспериментальных данных, которые необходимо интерпретировать [8–10] Ошибка! Закладка не определена. . Исследования в области математического моделирования гальваностатического режима ведутся по нескольким направлениям.
Первое направление — метод обратной задачи. Как ясно из названия, речь идет о решении обратной задачи: для заданной плотности тока на межфазной границе «раствор — мембрана» находится соответствующий скачок потенциала, а далее рассматривается задача для потенциостатического режима [11]. Низкая эффективность данного метода обусловлена тем, что его реализация требует многократного решения задачи в потен-циостатическом режиме для одного заданного значения плотности тока.
Второе направление — метод декомпозиции. При этом система уравнений Нернста — Планка — Пуассона заменяется системой декомпозиционных уравнений [12–16]. Предположение о квазиравномерном распределении заряда позволяет получить модель для гальваностатического режима в приближении закона Ома [17– 20].
Третий подход можно назвать прямым методом. В этом случае для плотности тока в канале обессоливания выводится уравнение, заменяющее уравнение Пуассона [21].
Гальваностатический режим можно описать иначе — с помощью численного решения уравнений Нернста — Планка — Пуассона для электрического потенциала со специальным граничным условием, которое позволяет установить плотность тока как параметр, задающий электрический режим в системе. В [22, 23] для одномерного случая производная по времени градиента электрического потенциала определялась как явная функция плотности тока. Это отличает подходы авторов указанных работ от потенциостатических моделей, в которых задается разность потенциалов.
В данной статье представлена стационарная модель процесса переноса ионов в мембранных системах для гальваностатического режима. Она основана на системе уравнений Нернста — Планка — Пуассона с граничным условием, которое позволяет установить плотность тока как параметр, задающий электрический режим в системе. В этом решение аналогично [22, 23]. Отличие же состоит в том, что предлагаемая модель двумерна и учитывает непостоянство плотности тока по длине канала.
Материалы и методы. Под мембранной системой подразумевается канал обессоливания электродиализного аппарата (ЭДА), образованный анионообменной (АОМ) и катионообменной (КОМ) мембранами. Через него со средней скоростью V 0 прокачивается раствор бинарного электролита. На рис. 1 х — нормальная к поверхности мембраны координата, изменяющаяся от 0 (граница с АОМ) до h (граница с КОМ); у — тангенциальная к поверхности мембраны координата, изменяющаяся от 0 (вход в канал) до l (выход из канала).
Информатика, вычислительная техника и управление
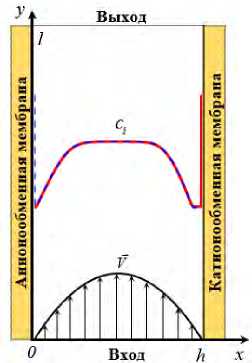
Рис. 1. Схема канала обессоливания ЭДА. Показаны концентрационные профили катионов С 1 (сплошная линия) и ^— анионов С 2 (пунктирная линия). Скорость вынужденного течения V
Система уравнений. Рассмотрим двумерный стационарный случай системы уравнений, описывающей перенос бинарного электролита в отсутствие химических реакций [24]:
- F _ „_ -
ji =--ztDi Ci Vф - D VCt + СV, i = 1, 2 , i RT i i ii i i
—
- div jt = 0, i = 1,2,(2)
EqEr Аф = —F (z 1C1 + z 2 C 2),
I = F (z 1 — + z 2 -2).(4)
—►
Здесь j i , D i , z i и C i — соответственно поток, коэффициент диффузии, зарядовое число и молярная концентрация i -го иона; ф — электрический потенциал; V — скорость потока раствора электролита; е 0 — электрическая постоянная; е r — относительная диэлектрическая проницаемость раствора электролита (предполагается постоянной); I — плотность тока; F — постоянная Фарадея; R — газовая постоянная; T — абсолютная темпе-
ратура; j 1 , j 2 , I , ф , Q , С 2 — неизвестные функции координат x и у .
Уравнения Нернста — Планка (1) описывают поток ионов, обусловленный миграцией в электрическом поле, диффузией и конвекцией; (2) — уравнение материального баланса в стационарном случае; (3) — уравнение Пуассона для потенциала электрического поля; (4) — плотность тока в растворе электролита. Будем считать, что распределение скорости в канале соответствует течению Пуазейля [24]:
V x = 0, V y = 6V 0 x 1 1 - x | . (5) h V h )
Для определения перечисленных выше неизвестных функций необходимо задать краевые условия для системы (1)—(3). Рассмотрим два электрических режима: потенциостатический, когда скачок потенциала на границах системы задается постоянным, и гальваностатический, когда постоянна плотность тока, протекающего через межфазную границу.
Граничные условия для моделирования потенциостатического режима. Будем считать поверхности ионообменных мембран эквипотенциальными. Система (1)–(4) включает потенциал электрического поля только в форме производных по пространственной координате. В этом случае существенным является только скачок потенциала Аф = ф ( h , у ) -ф (0, у ) , где Аф — известная функция, поэтому положим, например:
ф ( 0, У ) = 0 . (6)
Тогда
Аф = const .
Условия (6) и (7) определяют потенциостатический режим. Остальные граничные условия приводятся ниже.
На межфазной границе «АОМ — раствор» ( x = 0) концентрация коионов (катионов) определяется из условия непрерывности их потока у границы «мембрана — раствор» с учетом селективных свойств АОМ [16]:
fa С, F дф) ( 1 - T 2 ) I x (0, y )
I-- 1-- z С 1 ( 0, У ) =---------------------
( д x RT 11 д x J z 1 FD 1
где Ti (i = 1, 2) — эффективные числа переноса противоионов в мембране (КОМ и АОМ соответственно); Ti — числа, близкие к 1, причем для идеально селективной мембраны Ti = 1, и условие (8) превращается в условие непроницаемости мембраны для коионов.
Концентрация противоионов (анионов) зависит от обменной емкости КОМ, что можно задать в виде:
С ( 0 ,У ) = С 2 m = NSr
Здесь постоянная N a показывает, во сколько раз эта концентрация отличается от концентрации в объеме раствора [25].
На межфазной границе «раствор — КОМ» ( x = h ) для концентраций ионов приняты условия, аналогичные условиям на границе «АОМ — раствор» ( x = 0):
С ( h , У ) = С m = N c С 0 ,
fa с 2 F дф) ( 1 - T 1 ) I x ( h , У )
I + z? С? l ( h , У ) = •
( д x RT 22 д x J z 2 FD 2
На входе в канал (у = 0) принято равномерное распределение концентрации ионов:
C i ( x ,0 ) = С 0, i = 1,2.
Условие для потенциала электрического поля получено из уравнений (1) и (4) с учетом отсутствия протекания тока через вход I x ( x , 0, t ) = 0:
дф ( x ,0) _ RT f n д C 1 ( x ,0) _ д C 2 ( x ,0) )
---a =-- 2------- 5 --------1 z 1 D 1 + z 2 D 2 “ I.
дУ F (z 12 D1 + z 2 D 2) C 0 ( дУ 9yJ
На выходе из канала ( у = l ) ионы свободно выносятся потоком раствора:
--
(-, j ) = (-,- — zDa^ Уф- Div Ci + CiV) = С^, i = 1,2.(14)
Система (14) означает также, что сумма диффузионной и миграционной тангенциальных составляю- щих потоков анионов и катионов равна 0:
д Ci д У
_ F C дф RT i1 i д У
Для потенциала принято «мягкое» условие, означающее отсутствие резких изменений потенциала на
выходе из канала:
|ф ( x , l ) = 0. д У
Краевая задача, включающая уравнения (1)-(4) и краевые условия (6)-(16), моделирует потенциостати-ческий режим, причем его определяющее ключевое условие — (7).
Граничные условия для моделирования гальваностатического режима. При моделировании гальвано-статического режима условие (6) остается, а (7) необходимо заменить условием, связанным с заданным значением средней плотности тока iav на межфазной границе «раствор — КОМ» ( x = h ). Для вывода такого граничного условия подставим соотношения (1) в (4) и выразим градиент потенциала электрического поля:
Уф =-- гч -------2----- ( I + F ( z D 1 V С 1 + z 2 D 2 V С 2 ) - F ( z 1 C 1 + z 2 С 2 ) Т - ). (17)
F 2( z 2 D 1 C 1 + z 2 2 D 2 C 2 )
Полагая в (17) x = h , получаем соотношение, связывающее градиент электрического потенциала с заданным значением плотности тока на границе, то есть граничное условие на межфазной границе «раствор — КОМ»:
т RT — f дС, Ix+ Fz 1D1^ + Fz 2 D ax д С 2 ) F2 ( z 12D1С1 + z 22D 2 С 2 ' 2 ax^- (h , У )■ При этом плотность тока Ix должна удовлетворять условию: Информатика, вычислительная техника и управление
1 \
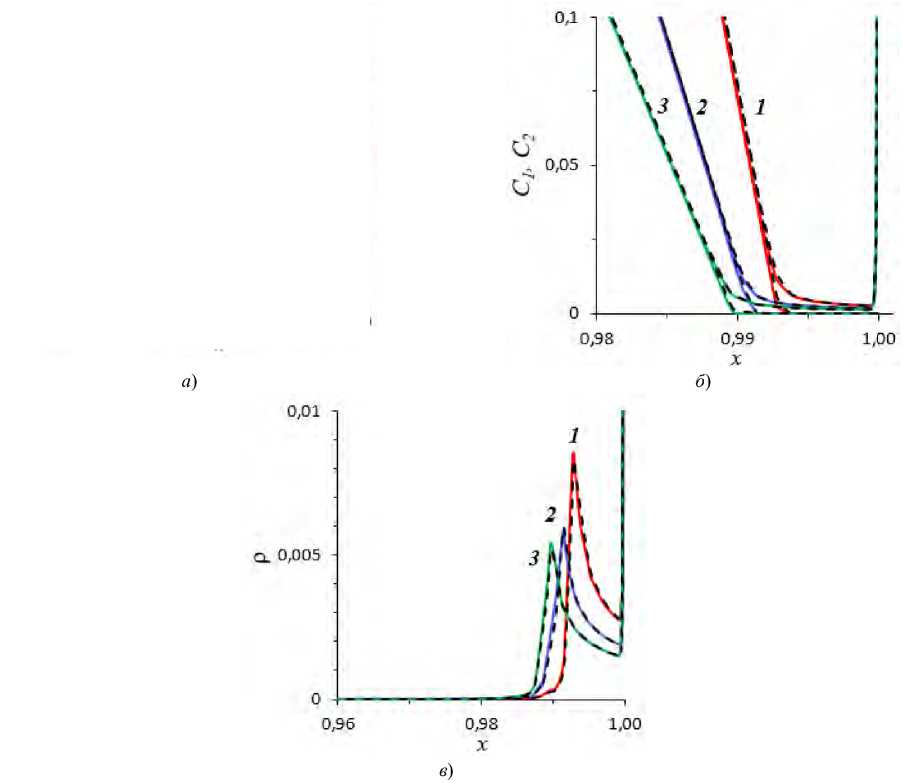
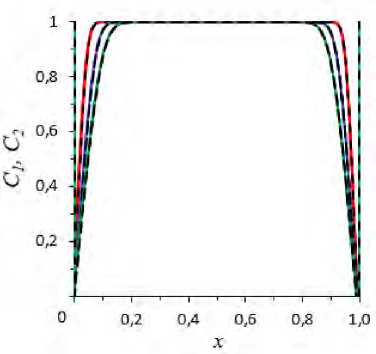
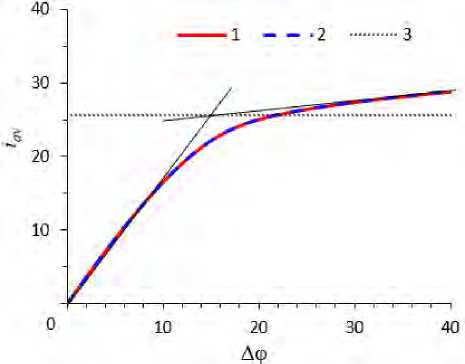
у] Ix (М) dy = iav l 0 Математическая модель гальваностатического режима состоит из системы уравнений (1)-(4). Граничные условия (18) и (19) заменяют условие (7). Остальные граничные условия совпадают с условиями для по-тенциостатического режима. Скачок потенциала в гальваностатическом режиме является вычисляемой величиной. Преобразование граничных условий для моделирования гальваностатического режима. Условие (19) неудобно для численного решения, так как содержит интеграл. Ниже приводится один из вариантов преобразования этого условия. В стационарном случае плотность тока I является соленоидальным вектором. Действительно, если умножить (2) на zi и сложить, то divI = 0. Следовательно существует такая функция п, что дл = I 0o = _t дx y, ду x . С использованием функции п условия (18) и (19) переписываются следующим образом: £( h,y ) = дx — RT F^ —^ + FzxDx С + FzD С 1 1 2 2 ду дx дx (h,y), 1 r 1 г дп -jIx(h,y) dy = —-J |^(h,y) dy = Iо 1о дУ — 1 (П (h,l) — П (h,0))= iav . Уравнение (22) можно переписать: n(hl)—n(h,0)= —U. Чтобы замкнуть систему выражений, необходимо получить уравнение для функции п. С этой целью, как и в работах [15, 16], введем в рассмотрение линейный дифференциальный оператор, который является функцией вихря (ротором) в двумерном случае, для произвольного двумерного вектора W : —— r (W) ГдWy д Wx ) — I дx ду X У . Несложно проверить, что: 1) r(Vи) = 0 для любой гладкой функции и ; —— —— —— ^— 2) r(uW) = (Vи, W) 1 + ur(W) для любой гладкой функции и и любого гладкого вектора W . —, ди ди — Здесь (Vи, W)1 = —Wy — —Wx — кососимметричное скалярное произведение векторов Vи и W , причем дx у ду (а, —)1 = 0 для любого вектора a . Применяя (24) к уравнению для плотности тока (4), получаем: —— —— — r (I ) = Fz 1r (j1) + Fz 2 r (j 2 )• Используя формулу потоков (1), получим соотношение: — F - r(Ji) = — ^, zD)r-(CiV^) — Dir(V Ci) + r(CiV), i = 1,2 . RT Отсюда с учетом свойств оператора r : r (h ) = — FZiDi(V Ci, Vф)1 +(V Ci, V—)1 + Cr (V—), i = 1,2 . RT — дIy дIx Учитывая (27) и r(I) =---= Ап , уравнение (25) можно записать: дx ду An = -—Лzv2Dv5-1 + z22D2 rt I 115x 21 5c2)5ф f2 5-12 5c2)дф) Zf D+ z. D->I + 5x J dy ( dy dy J 9x J ( Sc, Sc,) I Sc, Sc, ) +F z -1 + z,-2V - F z -1 + z,-2V + F (. ( 15x 25x J y ( 15y 2dy J x v Из (28) и (20) следует, что функция n определяется с точностью до константы, поэтому можно допу стить: П( h ,0) = 0. (29) Тогда из (23) получаем n(h,l) = -iavl . (30) Условия (29) и (30) — краевые для функции n ■ Математическая модель для гальваностатического режима в безразмерном виде. Для численного исследования краевых задач удобно перейти к безразмерному виду. Так можно упростить уравнения и выяснить фактическое количество и набор параметров, определяющих поведение системы. Безразмерные переменные описывают класс подобных процессов, характеризующихся одинаковым значением безразмерных чисел. Характерные величины, описывающие задачу. При моделировании процессов массопереноса в камере обессоливания ЭДА принимается ряд характерных значений: — для пространственных координат — межмембранное расстояние h ; — для концентраций ионов — объемная концентрация электролита С0 ; — для скорости — средняя скорость вынужденного течения V} ; — для коэффициентов диффузии — коэффициент диффузии электролита D = D 1 D2 (z 1 -z2)/(D 1 z 1-D2z2); — для электрического потенциала — тепловой потенциал ф0= RT/F ; — для плотности тока — величина i0 = FDC0/h (аналог предельной плотности диффузионного тока); — для потока ионов — диффузионный поток j0= DC0/h. Формулы перехода. Переведем уравнения в безразмерную форму с помощью следующих соотношений (индексом (и) обозначены безразмерные варианты величин): x(u) = x y(u) = y 1(u) = L v(u) —— V ^(u) УУ 12 , С1 , i1,2, V 0 С 0 hh h ’ (u) _ ф —(u) _ 1 ф , — (u) n , Fi u) = — ji, i = 1,2, Diu) = j 0 I , П ф0 i 0 FDC 0 Di . D Система уравнений в безразмерной форме имеет вид (индекс (и) для упрощения записи опущен): ———* ji = - ziDiCi Уф-Di V Ci + PeCiV, i = 1,2,(32) —* - div ji = 0, i = 1, 2,(33) еАф = -(z 1С1 + z 2 С2 ) , z,"D *1 + z*D & И 11^ 2 2 5x 5x J 5y — z,"D * + z2D & 1^*1+ 11^ 2 2 5y 5y J 5x J f 5- 5c2 1 +Pe z. —1+ z, — V I 15x 25x J y — Pe I zx5-1 + z2 —2 IV + Pe (. 1 2 x ( 5y 5y J , I = z 1 j1 + z 2 j2. Система уравнений (29)-(35) содержит два безразмерных числа: Pe = V3h/D число Пекле и е = еrе0RT(СС0h2F2). Физический смысл параметра е состоит в том, что это удвоенный квадрат безразмерной дебаевской длины lD : е = 2(lD/h)2[5]. Оценка величин параметров показывает, что при естественных для электродиализа условиях число Пекле имеет порядок 102-106, число е имеет порядок 10-13- 10-7 , то есть Информатика, вычислительная техника и управление может считаться малым параметром. Для удобства численного решения преобразуем систему уравнений, подставив плотность потока (32) в уравнения (33) и (36): I = £z, (- z,D, C, Vv - D, VС, + PeC,V). (38) г=1 Таким образом, система уравнений содержит следующие неизвестные функции x, у : С1, С2,V, Ix, Iy . Поля концентраций С1, С2 и потенциала ф определяются решением уравнений (37), (34) соответственно. Компоненты плотности тока Ix, Iy вычисляются с помощью (38). Распределение скорости (5) в безразмерной форме: Vx= о, Vy = 6 x (1 - x). Присутствие малого параметра с в уравнении Пуассона (34) означает, что краевая задача является сингулярно возмущенной. Это значительно усложняет ее численное решение, поскольку такие задачи относятся к жестким [26]. Потенциал электрического поля ф и концентрации ионов С1, С2 изменяются очень быстро в узком пограничном слое, толщина которого равна длине Дебая Id [5]. Для решения этой проблемы целесообраз- но уплотнить вычислительную сетку в пограничном слое и использовать специальные методы решения жест- ких задач [26]. Граничные условия в безразмерной форме. На межфазной границе «АОМ — раствор» (x = 0): (де, дф) (1 - т2) Ix (0, у) I+ z С 1(0, у) =, V дx 11lx 7 z1 D1 С2 (0, у ) = Na, ф(0,у )= ° |П(0,у ) = 0. дx На границе «раствор — КОМ» (x = 1): С1 (1, у ) = Nс, дС2 дф) (1 - T)Ix (1, у) --+ z2 С? — 1(1, у ) =---------------, дx 22Ix Jv 7 z2D2 l^ )= дx — ( дп п дС1 п дС2 ) - - + z1 D1 + z 2 D 2 , ду дx дx z2 D1С1 + z 2 D 2 С 2 (1, у) На входе в канал (у = 0): дф(x,0) _ бу — V д^у )=0. дx С,(х ,0) = 1, 1 ( , = 1,2, z1 D1+ z 2 D 2 дС дС2 ) _ + z2 D2^(x,0), ду ду 7 На выходе из канала (у = l): ( дС, --— бу z^|ф |(х, l)= 0,, = 1,2, бу у lv(x, l )= 0, (52) бу n(x,l) = -,avl, ,av = const. (53) После численного расчета системы (34), (35), (37)-(53) скачок потенциала Аф в канале обессоливания определяется по формуле: 1 l Аф = -|ф(1 ,У)dy . 1 0 Численное решение найдено методом конечных элементов с помощью пакета Comsol Multiphysics на неравномерной вычислительной сетке (плотность элементов сетки увеличена у границ «раствор — мембрана») [27]. Результаты исследования. Вычисления проведены для 8 = 1,9 -10 9, Pe = 2355 , что соответствует следующим значениям параметров системы: — входная концентрация раствора электролита NaCl C0 = 0,1 моль/м3; — температура T = 298 K; — коэффициенты диффузии катионов и анионов соответственно D 1 = 1,33*10-9 м2/с, D2 = 2,05*10-9 м2/с; — числа переноса противоионов в мембранах T1 = 0,972, T2 = 1; — зарядовые числа ионов z 1 = 1, z2 = -1; — отношение концентрации противоионов на границе с мембранами к ее значению на входе в канал Nc = Na = 1; — h = 10-3 м — ширина канала; — l = 2^ 10-3 м — длина канала; — V0 = 3,8-10-3 м/с — скорость прокачки раствора. На рис. 2 приведены поля концентраций C 1 и С2, потенциала ф и функции ц, рассчитанные при плотности тока iav = 1,5ilim, где ilim — это предельная плотность тока, определенная по формуле Левека (в безразмерной форме) [28]: — 0, 2 . Здесь 11 = 0,395 — число переноса катионов в растворе [9]. / , 9 X1 / 3 1, 471 ° I I ID J i = -*-lim T —t1 Информатика, вычислительная техника и управление Рис. 2. Поля концентрации катионов C 1 (а) и анионов С2 (б), потенциала ф (в) и функции ц (г). Расчет по модели для гальваностатического режима при плотности тока iav = 1, 5 ilim В канале действует вынужденное течение, поэтому в областях у мембран истощение концентрации ионов увеличивается при удалении от входа в канал (вдоль направления, тангенциального к поверхностям мембран). Соответственно, толщина расширенной области пространственного заряда увеличивается вдоль канала (рис. 3). Рис. 3. Результаты численного расчета по модели для гальваностатического (сплошные линии) и потенциостатического (пунктирные линии) режимов при плотности тока iav = 1, 5iUm в сечениях у = 0,11 (1), у = 0,41 (2), у = 0,91 (3): концентрационные профили C 1 и С2 (а); увеличение рис. 3, а (б); плотность пространственного заряда р = z 1 C + z2C2 (в) Вольтамперная характеристика (ВАХ, кривая 1 на рис. 4) рассчитана на основе гальваностатической модели. При этом задаваемая плотность тока изменялась: iav= 0; 0,005iiim; ...; 1,5iiim. Рис. 4. ВАХ, рассчитанные по моделям для гальваностатического (1) и потенциостатического (2) режимов; предельная плотность тока iiim (3) определена по формуле (55) Предельная плотность тока определена по точке пересечения касательных к ВАХ в начальной части и на наклонном плато [5]. Здесь она совпадает со значением ilim, оцененным по приближенной формуле Левека (55). Также ВАХ была рассчитана на основе потенциостатической модели при изменении скачка потенциала ∆φ = 0; 0,4; …; 40 (кривая 2 на рис. 4). Как видно из рис. 4, ВАХ 1 и 2 совпадают. Таким образом, существует однозначное соответствие каждому скачку потенциала некоторой плотности тока, и наоборот. Рис. 3 и 4 демонстрируют достаточно хорошее совпадение различных физико-химических характеристик переноса, рассчитанных по моделям для гальваностатического и потенциостатических режимов. Это доказывает адекватность построенной авторами модели переноса в гальваностатическом режиме. Вычислительные затраты предлагаемой модели оценивались следующим образом. Фиксировалось время, затраченное на решение краевых задач для гальваностатического и потенциостатического режимов. При этом значения задаваемой точности вычислений, параметры системы были одинаковыми, а ат = 1, 51m . Затем показатели времени сравнивались. Таким образом выяснилось, что расчет по гальваностатической модели требует в 1,6 раз больше времени. Это связано с тем, что: — гальваностатическая модель содержит дополнительное уравнение для определения распределения плотности тока; — для потенциала на границе x = 1 установлено условие второго рода (46). Комплексный потенциал электромембранной системы для гальваностатического режима. В работе [25] предложено обобщение импеданса электрохимической системы с помощью функции п, введенной в условиях электронейтральности. Аналогичное обобщение приемлемо и в данном случае. Отметим, что при использовании электрохимического импеданса объект рассматривается только как «черный ящик», и его внутренние свойства определяются косвенно. Полученные выше результаты позволяют ввести понятие комплексного потенциала электромембранной системы: P = ф +1 • п . Комплексный потенциал — это функция координаты любой точки внутри объекта, поэтому, в отличие от электрохимического импеданса, он позволяет исследовать внутренние свойства объекта. Обсуждение и заключения. Описан новый метод математического моделирования стационарного процесса массопереноса в гальваностатическом режиме для мембранных систем. При этом рассмотрен двумерный случай с использованием специального граничного условия, позволяющего задать плотность тока в системе. Представлены уравнения для электрической функции тока. Результаты численного решения по потенцио-статической и гальваностатической моделям хорошо согласуются. Это показывает адекватность предлагаемой модели переноса в гальваностатическом режиме. Разработанная модель позволяет интерпретировать результаты экспериментальных исследований переноса ионов в мембранных системах, если данный процесс протекает в гальваностатическом режиме. Некоторые электрокинетические процессы связаны с появлением расширенной области пространственного заряда при сверхпредельных токах. Описывая формирование указанной области, можно выяснить, каким образом зависящие от нее процессы влияют на перенос ионов в гальваностатическом режиме.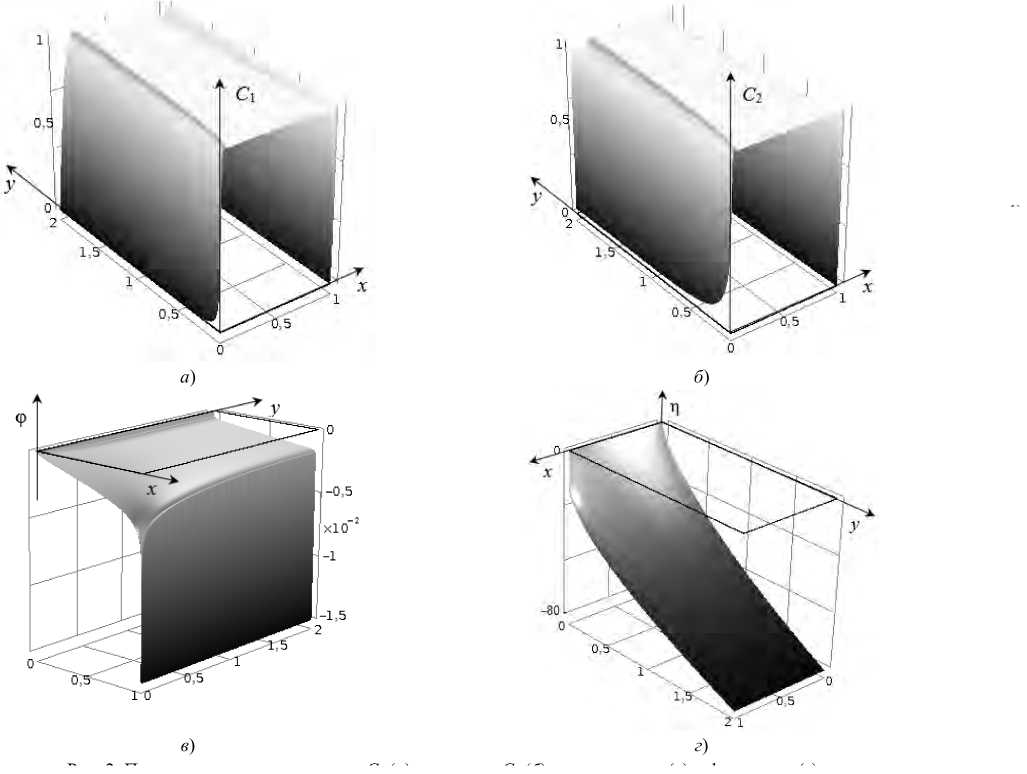
Список литературы Стационарная модель переноса ионов соли в двумерном электродиализном канале обессоливания в гальваностатическом режиме
- Science and technology for water purification in the coming decades/M.-A. Shannon//Nature. -2008. -Vol. 452 (7185). -P. 301-310. - DOI: https://doi.org/10.1038/nature06599
- Direct seawater desalination by ion concentration polarization/S.-J.Kim//Nature Nanotechnology. -2010. -V. 5. -P. 297-301. - DOI: https://doi.org/10.1038/nnano.2010.34
- Kim, S.-J.Nanofluidic concentration devices for biomolecules utilizing ion concentration polarization: theory, fabrication, and applications/S.-J. Kim, Y.-A. Song, J. Han//Chemical Society Reviews. -2010. -Vol. 39 (3). -P. 912-922. - DOI: https://doi.org/10.1039/b822556g
- Elimelech, M. The Future of Seawater Desalination: Energy, Technology, and the Environment/M. Elimelech, W.-A.Phillip//Science. -2011. -Vol. 333. -P. 712-717. - DOI: https://doi.org/10.1126/science.1200488
- Intensive current transfer in membrane systems: Modelling mechanisms and application in electrodialysis/V. V. Nikonenko//Advances in Colloid and Interface Science. -2010. -Vol. 160. -P. 101-123. -DOI: https://doi.org/10.1016/j.cis.2010.08.001
- Desalination at overlimiting currents: State-of-the-art and perspectives/V. V. Nikonenko//Desalination. -2014. -Vol. 342. -P.85-106. -DOI: https://doi.org/10.1016/j.desal.2014.01.008
- Effect of electroconvection and its use in intensifying the mass transfer in electrodialysis (Review)/V. V. Nikonenko//Russian Journal of Electrochemistry. -2017. -Vol. 53 (10). -P. 1122-1144. -DOI: https://doi.org/10.1134/S1023193517090099
- Effect of Anion-exchange Membrane Surface Properties on Mechanisms of Overlimiting Mass Transfer/E. I. Belova//Journal of Physical Chemistry. B. -2006. -Vol. 110. -P. 13458-13469. - DOI: https://doi.org/10.1021/jp062433f
- Effect of counterion hydration numbers on the development of Electroconvection at the surface of heterogeneous cation-exchange membrane modified with an MF-4SK film/V. V.Gil//Petroleum Chemistry. -2016. -Vol. 56 (5). -P. 440-449. -DOI: https://doi.org/10.1134/S0965544116050066
- Effect of surface hydrophobization on chronopotentiometric behavior of an AMX anion-exchange membrane at overlimiting currents/E.Korzhova//Journal of Membrane Science. -2016. -Vol. 500. -P. 161-170. -DOI: https://doi.org/10.1016/j.memsci.2015.11.018
- Лаврентьев, А. В. Математическое моделирование переноса в электромембранных системах с учетом конвективных течений/А. В. Лаврентьев, А. В. Письменский, М. Х. Уртенов. -Краснодар: Изд-во КубГТУ, 2006. -147 с.
- Model and Experimental Studies of Gravitational Convection in an Electromembrane Cell/A. V. Pismensky//Russian Journal of Electrochemistry. -2012. -Vol. 48(7). -P. 830-841. -DOI: https://doi.org/10.1134/S1023193512070075
- Коваленко, А. В. 3D-моделирование переноса бинарного электролита в гальваностатическом режиме в условиях электронейтральности/А. В. Коваленко, Е. В. Казаковцева, М. Х. Уртенов//Научный журнал КубГАУ. -2015. -№ 110 (06). -C.1-12. -Режим доступа: http://www.ej.1gb.ru/2015/06/pdf/23.pdf (дата обращения 02.03.18).
- Chronopotentiometric Response of Electrically Heterogeneous Permselective Surface: 3D Modelling of Transition Time and Experiment/S. A. Mareev//Journal of Physical Chemistry. C. -2016. -Vol. 120. -P. 13113-13119. -DOI: https://doi.org/10.1021/acs.jpcc.6b03629
- Мареев, С. А. Одномерное моделирование результатов хронопотенциометрии в сверхпредельных токовых режимах/С. А. Мареев//Конденсированные среды и межфазные границы. -2015. -Т. 17, № 2. -С. 171-180. -Режим доступа: http://www.kcmf.vsu.ru/resources/t_17_2_2015_006.pdf (дата обращения 05.11.18).
- Chronopotentiometry of ion-exchange membranes in the overlimiting current range. Transition time for a finite-length diffusion layer: modeling and experiment/S. A. Mareev//Journal of Membrane Science. -2016. -Vol. 500. -P. 171-179. -Режим доступа: https://doi.org/10.1016/j.memsci.2015.11.026 (дата обращения 05.11.18).
- Анализ краевой задачи модели переноса бинарного электролита в приближении закона Ома/А. В. Коваленко//Научный журнал КубГАУ. -2012. -№ 77 (03). -С.1-14. -Режим доступа: http://ej.kubagro.ru/2012/03/pdf/57.pdf (дата обращения 05.11.18).
- Численное решение краевой задачи модели переноса бинарного электролита в приближении закона Ома/А. В. Коваленко//Научный журнал КубГАУ. -2012. -№ 77 (03). -С.1-16. -Режим доступа: http://ej.kubagro.ru/2012/03/pdf/58.pdf (дата обращения 05.11.18).
- Хромых, А. А. Асимптотическое решение краевой задачи модели ЗОМ тернарного электролита/А. А. Хромых, А. В. Коваленко, М. Х. Уртенов//Фундаментальные исследования. -2014. -№ 8, ч. 3. -С. 600-606.
- Kovalenko, A. V. Decomposition of the two-dimensional Nernst-Planck-Poisson equations for a ternary electrolyte/A. V. Kovalenko, A. A. Khtomykh, M. K.Urtenov//Doklady Mathematics. -2014. -V. 90 (2). -P. 635-636. -DOI: https://doi.org/10.1134/S1064562414060271
- Коваленко, А. В. 2D-моделирование переноса ионов соли для бинарного электролита в гальванодинамическом режиме/А. В. Коваленко, А. М. Узденова, М. Х. Уртенов//Экологический вестник научных цен-тров Черноморского экономического сотрудничества. -2013. -№ 3. -С.67-76.
- Numerical Simulation of the Nonequilibrium Diffuse Double Layer in Ion-Exchange Membranes/J.-A.Manzanares//Journal of Physical Chemistry. -1993. -Vol. 97. -P. 8524-8530. - DOI: https://doi.org/10.1021/j100134a023
- Moya, A.-A. Electrochemical impedance of ion-exchange systems with weakly charged membranes/A.-A. Moya//Ionics. -2013. -Vol. 19. -P. 1271-1283. -DOI: https://doi.org/10.1007/s11581-013-0850-0
- Newman, J.-S. Electrochemical systems/J.-S. Newman. -New Jersey: Prentice Hall, 1973. -464 p.
- Rubinstein, I. Voltage against current curves of cation exchange membranes/I. Rubinstein, L.Shtilman//Journal of the Chemical Society Faraday Transactions. -1979. -Vol. 75. -P. 231-246. - DOI: https://doi.org/10.1039/F29797500231
- Doolan, E.-P. Uniform numerical methods for problems with initial and boundary layers/E.-P. Doolan, J.-J.-H. Miller, W.-H.-A.Schilders. -Dublin: Boole Press, 1980. -324 p.
- Математическое моделирование физико-химических процессов в среде ComsolMultiphysics 5. 2/А. В. Коваленко. -Санкт-Петербург: Лань, 2017. -228 с.
- Мембраны и мембранные технологии/Под. ред. А. Б. Ярославцева. -Москва: Научный мир, 2013. -612 с.
- 2D-моделирование переноса бинарного электролита в электромембранных системах/А. В. Коваленко//Известия Кубан. гос. ун-та. Естественные науки. -2013. -№ 2. -С.52-57.


