Стационарные характеристики ненадежной системы с ветвящейся структурой и учетом технического обслуживания ее элементов
Автор: Песчанский Алексей Иванович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии компьютерных систем и сетей
Статья в выпуске: 1 т.17, 2019 года.
Бесплатный доступ
Объектом исследования является система с ветвящейся структурой древовидного типа, в которой каждый элемент некоторого ранга управляет несколькими элементами более низкого ранга и управляется одним элементом более высокого ранга. В процессе функционирования системы ее элементы могут отказывать, но восстанавливать свои характеристики в результате ремонтных работ. Предполагается, что все случайные величины, описывающие систему, имеют распределения общего вида. Для улучшения надежностных и экономических стационарных показателей функционирования системы предлагается проводить предупредительное техническое обслуживание элементом со стратегией, известной как «восстановление в зависимости от возраста». В этом случае получены итерационные формулы для расчета коэффициента технического использования, среднего удельного дохода и средних удельных затрат системы, которые позволяют находить оптимальные сроки проведения технического обслуживания ее элементов.
Линейная ветвящаяся структура, техническое обслуживание "по возрасту", стационарный коэффициент технического использования, средний удельный доход, средние удельные затраты, оптимизация сроков проведения технического обслуживания
Короткий адрес: https://sciup.org/140256211
IDR: 140256211 | УДК: 519.872 | DOI: 10.18469/ikt.2019.17.1.07
Текст научной статьи Стационарные характеристики ненадежной системы с ветвящейся структурой и учетом технического обслуживания ее элементов
Многие технические системы имеют иерархическую или ветвящуюся структуру, в которой каждому элементу некоторого ранга непосредственно подчинено несколько элементов более низкого ранга. Примерами являются системы обработки данных, системы и сети связи, транспортные и ресурсо-снабжающие сети (трубопроводные, электрические, энергетические и т.д.). Обеспечение работоспособности таких систем является важной задачей [1-4]. Основное внимание исследователей сосредоточено на двух направлениях: разработка эффективных методов вычисления характеристик, существенных для анализа надежности и эффективности структур; разработка методов повышения надежности и улучшения экономических показателей таких структур [5-10].
Целью статьи является построение итерационного процесса расчета стационарных надежностных и экономических характеристик линейной сетевой структуры древовидного типа с учетом проведения технического обслуживания ее элементов. Предполагается, что времена безотказной работы и восстановления элементов суть случайные величины с функциями распределения общего вида.
Отметим, что в линейной структуре каждый ее элемент имеет связь только с элементами соседних рангов, но не имеет связей в пределах одного ранга и через несколько рангов. В статье рассматривается стратегия обслуживания, известная в литературе под названием «восстановление в зависимости от возраста» [9], или «правило предупредительных замен» [10].
Для однокомпонентных систем данная стратегия исследована в [8-10], а для многокомпонентной системы с монотонной структурой – в [11-13].
Постановка задачи
Рассмотрим ненадежную систему с ветвящейся структурой (см. рисунок 1), где головной элемент а^ связан с сц элементами первого ранга, каждый из которых в свою очередь связан с аг элементами второго ранга и т.д.
Каждый из элементов предпоследнего (л-1) ранга связан с an элементами последнего n -го ранга, которые называют выходными.
Число элементов i -го ранга равно N, = П й/ ’ ' = 1, n .
k=\
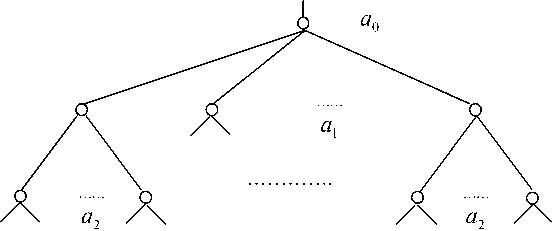

Рисунок 1. Схема линейной однородной ветвящейся структуры
Будем рассматривать однородную систему: это означает, что элементы одного ранга однотипны. Пусть оц – время безотказной работы элемента i-го ранга с функцией распределения F,^ = Р(а, < t), i = 0,п ; а Pi – время восстановления элемента i-го ранга с функцией распределения С,(П = Р^<П, i = ^. Предположим, что указан- ные случайные величины имеют конечные математические ожидания: Еа; и Epx соответственно.
Отказ любого элемента системы, который будем называть аварийным, обнаруживается мгновенно и сразу же начинается его восстановление . В момент аварийного отказа элемента прекращается как работа, так и восстановление всех связанных с ним элементов, кото- рым он предшествует. Также отключаются все элементы, которые предшествуют отказавшему элементу и не принадлежат более ни одному работоспособному пути. Под работоспособным путем подразумевается цепочка функционально связанных работающих элементов от головного элемента до одного из выходных.
В момент включения в систему восстановившегося элемента одновременно с ним включаются и те, ранее отключенные работоспособные элементы, которые вместе с восстановленным элементом образуют работоспособный путь. При этом их уровень работоспособности такой же, каким он был при отключении. Кроме этого, продолжается восстановление отключенных элементов, связанных функционально с восстановленным элементом.
Система считается отказавшей, если она не содержит ни одного работоспособного пути от головного элемента до выходного. В этот момент все оставшиеся работоспособные элементы отключаются. Итерационный процесс расчета стационарного коэффициента готовности такой системы построен в [14].
Одним из методов повышения надежности и эффективности описанной системы может быть предупредительное техническое обслуживание (ТО) каждого элемента системы со стратегией «восстановление в зависимости от возраста» [9]. Суть этой стратегии заключается в том, что если элемент после завершения очередных восстановительных работ проработал некоторый заранее заданный промежуток времени, то проводится его предупредительное техническое обслуживание.
В начальный момент времени t = о начинается эксплуатация системы и назначае тс я допустимый уровень наработки (возраст) Tj , z = 0, n элемента системы, одинаковый для всех элементов i -го ранга. Если после завершения восстановительных работ элемент проработал без отказа время Ti ’ то проводится плановое ТО элемента, которое его полностью обновляет.
Так же, как и в моменты аварийного отключения, в моменты начала ТО элемента и его завершения происходит отключение и включение функционально связанных с ним элементов .
Длительность ТО – это случайная величина
Pi
с функцией распределения
cptvp^ = 0, n и конечным математическим ожиданием Epf. Если до назначенного момента времени T; элемент системы отказывает, то начинается его аварийное восстановление, в результате которого элемент также полностью обновляется, и весь процесс обслуживания элемента повторяется заново. Предполагаются известными следующие экономические показатели элементов системы: Cj – доход в единицу времени безотказной работы элемента i-го ранга, i = 0, и; c® – затраты в единицу време- ни аварийного восстановления элемента i-го ранга, i = 0,n; cf – затраты в единицу времени технического обслуживания элемента i-го ранга, i = 0,n. Целью работы является определение следующих показателей качества функционирования системы: – стационарного коэффициента технического использования системыЦт6,ть...,тР; – среднего удельного дохода Sy0,Tv...,T,y системы, приходящегося на единицу календарного времени; – средних удельных затрат СУ0,тх,...,т„У приходящихся на единицу времени исправного функционирования системы. Также требуется определить оптимальные сроки Ti проведения технического обслуживания элементов системы, при которых показатели качества функционирования системы принимают наилучшие значения. Определение стационарных характеристик системы Построим итерационный процесс расчета стационарных показателей системы. Для этого введем следующие обозначения: ЗД) – коэффициент готовности элемента i-го ранга, i-O.n; ^I ^i) – средний удельный доход в единицу времени функционирования элемента i-го ранга, i = O,n; С^тр – средние удельные затраты в единицу времени исправного функционирования элемента i-го ранга, i = 0,n . Данные характеристики элементов i-го ранга определяются следующими формулами [9-11]: K.^ =____^____• g \ — ^i ^i ^i) ^i ^i ^ i -^ ^' ^ ^i ^ ’ m Л J Р Чт^ + Р Чт^ + тРрт^ (1) C^x^T^rp + cfT^) A J тр^ ’ где T44TP=V0FPtW – среднее время работоспособности; Т^Чтр = ЕЛтРЕр; – среднее время аварийного восстановления; Т^УУ = Е^)ЕрР – среднее время ТО элемента i-го ранга на периоде регенерации, то есть между двумя соседними моментами начала работы элемента после завершения аварийного восстановления или ТО. Далее введем аналогичные характеристики для одного семейства из a. элементов, которые управляются одним и тем же элементом из (i — 1) -го ранга, i = 1,11 (см. рисунок 2). Заметим, что семейство считается работоспособным, если работоспособен хотя бы один элемент этого семейства. Очевидно, что показатели будут зависеть от сроков проведения ТО элементом i-го и всех последующих рангов. Обозначим к'-Чт^-д,.) – коэффициент технического использования; 5иЧт^..,т„) – средний удельный доход в единицу времени функционирования; Си\т;,...,т,Ч – средние удельные затраты в единицу времени исправного функционирования такого семейства. Рисунок 2. Схема семейства i-го ранга При построении итерационных формул для определения стационарных показателей системы с ветвящейся структурой используем результаты [11], где при помощи аппарата теории полумар- ковских процессов с дискретно-непрерывным фазовым пространством состояний [15] получены расчетные формулы для нахождения стаци- онарных характеристик ненадежной многоком- понентной системы с монотонной структурой с учетом ТО по возрасту и отключением элементов. В частности, коэффициент технического ис- пользования K, средний удельный доход S и средние удельные затраты C системы, состоящей из N последовательных элементов, есть N V N S-K^; С = 2С,., /=1 А м где К,, s„ с, – характеристики элементов системы. В случае параллельного соединения элементов системы эти характеристики есть k^y-пЧ-кЧ; S = ^S/, с = —--- Семейство из а выходных элементов n-го ранга, которые управляются одним и тем же элементом (n-1)-го ранга, будет находиться в отказе, если откажут все элементы этого семейства. Поэтому для определения стационарных характеристик такого семейства применим формулы (3) стационарных характеристик системы с параллельным соединением: ^J = i4i-^,,)b; S^4r,4 = a„S,^„Y При нахождении характеристик семейства элементов (n-1)-го ранга, управляемых одним и тем же элементом (n-2)-го ранга, применим комбинации формул характеристик системы с параллельным (3) и последовательным соединениями элементов (2). Рассмотрим систему из параллельных элементов (n-1)-го ранга, каждый из которых соединен последовательно с семейством элементов n-го ранга. В результате получим su,-'4r„_x s„x(rn x) ! s("'(r„) K„_x(^ К'пЧт„) . 1+ь^(г^+Ь£22Ы ’ С„_Агп^ + С^Чт^ у + \-кот^+\-кЧчЧь1 ^n-i(^,-i) К^Чг,^ I к„_Аг„^ к^Чт,,} ) Для семейства элементов m-го ранга, где шения, которые после ряда преобразований т = 1, п -1, имеют место аналогичные соотно- принимают следующий вид: ^'">(г„„...,г„) = 1- AUrJ + Ar('"+1,(rm+1,...^ ^Жы^^^^ /=0 Характеристики головного элемента а^ определяются с помощью формул для системы из последовательно соединенного головного элемента и системы элементов первого ранга. Они являются характеристиками всей системы с ветвящейся структурой в целом и определяются формулами: При пас- К<г0,тх,...т,^ = к0^ ку\тх,..^,р-k0(j^ 5(г0,г,,...,г„) = S0(r0)K^4rv,...,r^ + K0(r0)Sm . К0(т0) + К^Чгх,...,т,3-К0(т0^АЧгх,^ С(г0,г„...,г„) = С0(г0) + а, [с, + С2) 1^ + АГ*2* - ^Л?12* J'1 х'к + кт -2кхк11^ [аг, + кт -^1^(2)]'|“'“1 2 = 0 сивной стратегии обслуживания, когда ТО элементов не проводится, в итерационные формулы (4)-(6) следует подставить следующие соотношения: К,„ =-------5----, m = 0, и ; E«m*EPm К''"'* =1— Ео^т . _Еат + ЕРт\ ’ s = стЕат -стЕРт m=Q-n Еа„ЛЕрю ^(н) _ Ст Е®т — Ст ЕРт . “ " Еа„ЛЕРт ’ с° ЕВ __ Ст = ™ р™ , т = 0,и; Еат ^ий _ апСцЕРп К''-\Еа„+Ер„У Заметим, что в этом случае коэффициент готовности K совпадает с известной формулой в [14]. Частный случай системы Рассмотрим систему с ветвящейся структурой, изображенной на рис.1, при условии, что все случайные величины, ее определяющие, имеют показательное распределение, а именно: Р,(.П = 1- е"^', G,(?) = 1 - е^1', Gf (П = 1 - е"м?*, i = 0,п. В этом случае в (4)-(6) для вычисления стационарных характеристик системы следует полагать т = 0, п; С и -^rn^rnHm-L^mtm _ iV ^тМгп cm/vm р v / ^т ^т) ,т = О,п; Sw(Tn) = anSn(Tn); ^^^(^"'-хУ' Мт С„Дтт) = ^ + ^ W"'™ - 1)г’, т = 0, л ; Мт Мт Оптимизация периодичности проведения ТО элементов системы Стационарные характеристики (6) системы с ветвящейся структурой явно зависят от пороговых значений возрастов элементов, при до стижении которых принимается решение о проведении ТО. Поэтому задача определения оптимальных сроков проведения ТО элементов системы сводится к задаче нахождения точек абсолютного экстремума выбранной критериальной функции: КДг0, г,,... тп)^ max _ ; т, е(0,со); 1=0,п S (r0, г,,... r„)-> max _ . Tj g(O,cc); i=O,n С (г0, r,,... r„) ^ min . Ttg(O,cc);z=O,/2 Приравнивая к нулю частные производные функций К<т0,тх,...т,Д, S^T0,Tv...r^ и C(r0, ^„..rj, получаем соответственно системы уравнений, которым удовлетворяют оптимальные значения наработок: —^(r0, r1,...r„) = O, i = O,n ; dr,. — S(r0, r1,...r„) = O, i = O,n; — C(ro,r1,...r„) = O, Z = O,/7. dr,. Можно показать, что система уравнений (7) для определения критиче ских точек функции ^(Го,^,...^,) равносильна системе уравнений ——— = 0, z = 0,/7 . dr, Таким образом, система будет иметь максимальный коэффициент использования при таких сроках проведения ТО, при которых достигается максимальное значение коэффициента техниче ского использования каждого элемента системы. Заметим, что техническое обслуживание не всегда приводит к улучшению стационарных характеристик системы. Так, в случае показательного распределения всех случайных величин, описывающих систему, проведение ТО элементов только снижает коэффициент технического использования. Положительный эффект от проведения ТО следует ожидать в том случае, когда со временем возрастает интенсивность отказов элементов, а затраты и время на проведение их ТО значительно меньше соответствующих показателей в случае аварийных отказов. Численный пример Рассмотрим линейную однородную систему с ветвящейся структурой, которая содержит элементы четырех рангов kn = 3Y Времена безотказной работы at, аварийного восстановления Pi и технического обслуживания Pf имеют соответственно распределения Эрланга с функциями распределения: РДМ) = 1 - e"^ f(^^, ОДО = 1 - e^1 Tp1^, 7=0 >! 7=0 J! ^(0 = 1-е~лЛЕ(^ ■ 7=0 j\ В таблице 2 через Kx, S'. c обозначены показатели качества функционирования системы в случае, когда используется пассивная стратегия обслуживания, то есть ТО элементов не проводится. Таблица 1. Исходные данные системы для численного примера св св Он ^ Число элементов в семействе ранга Среднее время безотказной работы Ма, сут Среднее время восстанов ления МД,сут. Среднее время ТО Mpf,4a£ Доход элемента с,,ден. ед./мес. Затраты на восстановление с,°, ден. ед./мес. Затраты на ТО cf, ден. ед./мес. 0 а0 =1 400 8,6 21,3 1500 1800 500 1 «! = 3 150 6,0 19,3 1200 1400 300 2 а2 =3 109 4,6 18,8 1000 1000 200 3 «з=2 92,3 3,8 17,3 1000 700 200 Таблица 2. Результаты оптимизации характеристик системы по различным критериям Св Щ св Пи ^ С сут. j^-max К® У, СУТ. ^ max ден. ед./мес. S”, ден. ед./мес. с, Сут. £,min Ден. ед./мес. С”, ден. ед./мес. 0 131,8 0,987 0,969 129,6 29050,7 25641,4 83,1 320,6 1443,0 1 55,1 52,6 27,9 2 44,7 40,1 22,9 3 40,1 34,0 23,5 Проведение ТО элементов при достижении времен безотказной работы элементов г,У r,s, ^,1 = 03; в зависимости от выбранного критерия, улучшает эти показатели соответственно на 1,86%; 13,30% и 77,78%. Выводы В статье представлен итерационный процесс расчета стационарных надежностностных и экономических характеристик ненадежной системы с линейной однородной ветвящейся структурой с учетом проведения технического обслуживания ее элементов по возрасту. На примере системы с конкретной сетевой структурой показана возможность определения оптимальных сроков проведения технического обслуживания. При этом коэффициент технического использования системы увеличивается незначительно, но доходность системы может быть значительно увеличена, а затраты существенно снижены. Заметим, что по аналогичной методике можно получить расчетные формулы для стационарных характеристик системы в случае других стратегий проведения ТО ее элементов и выбрать оптимальную из них.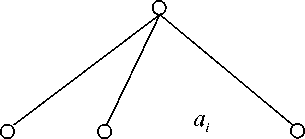
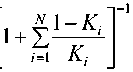
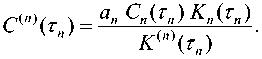
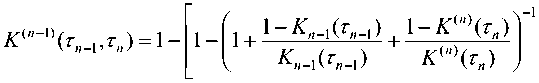
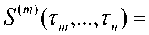
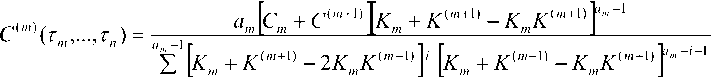
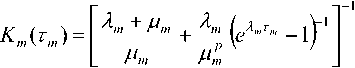
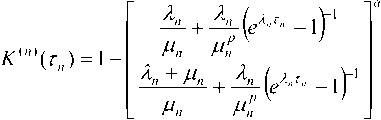

Список литературы Стационарные характеристики ненадежной системы с ветвящейся структурой и учетом технического обслуживания ее элементов
- Надежность систем энергетики и их оборудования: Справочник в 4 т. Под ред. Ю.Н. Руденко. Т.1. Справочник по общим моделям анализа и синтеза надежности систем энергетики. - М: Энергоатомиздат, 1994. - 472 с.
- Надежность систем энергетики и их оборудования: Справочник в 4 т. Под общ. ред. Ю.Н. Руденко. Т.4. Надежность систем теплоснабжения. - Новосибирск: Наука, 2000. - 351 с.
- Сеннова Е.В., Кирбхин С.Н., Шиманская А.О. Методология и алгоритм расчета показателей надежности теплоснабжения потребителей и резервирования тепловых сетей при разработке схем теплоснабжения // Новости теплоснабжения // URL: http://www.ntsn.ru/ (д.о. 16.10.2018).
- Скворцов М.С. Методика оптимизации систем с сетевой структурой // Труды СПИИРАН. - 2011. - Вып. 1(16). - С.231-242.
- Черкесов Г.Н. Оценка надежности систем с учетом ЗИП. - СПб.: БХВ-Петербург, 2012. - 480 с.


