Стационарные и динамические процессы в технологических печах

Для высокотемпературного нагрева нефти и нефтепродуктов в процессе их переработки в ректификационных установках применяют трубчатые печи. Печи работают следующим образом [1]. Мазут и газ сжигаются в горелках, расположенных в камере радиации. Продукты сгорания из камеры радиации поступают в камеру конвекции, затем направляются в газосбор-ник и по дымовой трубе уходят в атмосферу. В камере конвекции расположены конвекционные трубы, воспринимающие тепло при соприкосновении дымовых газов с поверхностью нагрева путем конвекции. Нагреваемый продукт в печи последовательно проходит через конвекционные и радиантные трубы, поглощая тепло. Радиантная поверхность воспринимает большую часть тепла, выделяемого при сгорании топлива (рис. 1).

Горение жидкого топлива всегда протекает в паровой фазе, причем испарение обеспечивается подводом тепла из зоны горения паров. Топливо всегда сжигается в распыленном виде. Крайним случаем горения капель является диффузионное горение, когда скорость сгорания паров очень велика по отношению к скорости диффузии паров и окислителя в зоне горения, толщина которой становится исчезающе малой. К такому режиму может приближаться горение сравнительно круглых капель. Диффузионная теория горения развита Г.А. Варшавским [2].

Математические модели теплофизических процессов

В математических методах анализа процесса горения у разных авторов имеются некоторые расхождения, но для стационарного сферического горения используется единый подход. В целях упрощения анализ проводится при следующих предположениях:

• 1.    Жидкая капля имеет сферическую форму.

• 2.    Влиянием конвекции пренебрегают, пламя рассматривают как сферическую поверхность, концентрическую с каплей.

• 3.    Пламя считают разновидностью диффузионного пламени, которое образуется в результате реакции между парами горючего и воздухом, которые реагируют в стехиометрическом соотношении.

• 4.    Рассматривают стационарное состояние при постоянном диаметре капли, хотя реально диаметр жидкой капли уменьшается по мере горения, однако это изменение происходит медленно по сравнению с изменением скорости диффузии и прочими факторами.

• 5.    Температура капли одинакова по всему объему.

• 6.    Давление в течение всего процесса горения считается постоянным.

• 7.    Влияние излучения рассматривают отдельно [36].

  
  
  

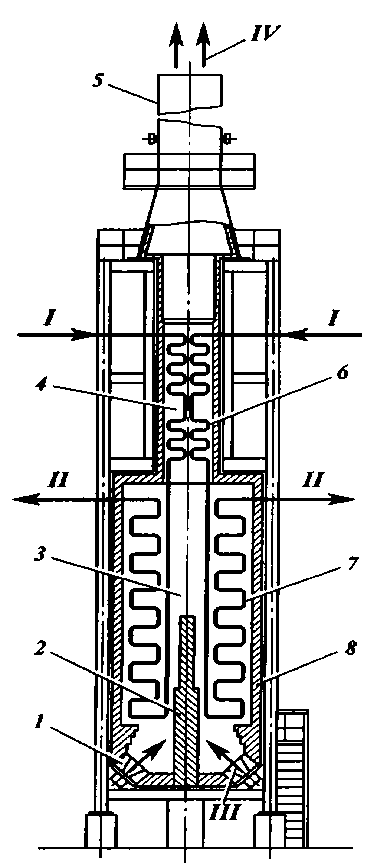
Рис. 1. Схема трубчатой печи: 1 – горелка; 2 – настильная стенка; 3 – камера радиации (топочная камера); 4 – камера конвекции; 5 – дымовая труба; 6 – змеевик конвекционных труб; 7 – змеевик радиантных труб; 8 – футеровка. Потоки: I – вход сырья; II – выход сырья; III – топливо и воздух; IV – дымовые газы

Исходя из законов механики сплошных сред, можно получить следующие уравнения не- стационарного горения:

д р      д р    д и

— — — и--р—,д t      д l Р д I

д -и

—1

дx

д t

— и — д l

d x x

—

, τ

д t

• и ^и. — R ^{- Т}п д l      д l

—

RT п д р

р дг

^ = (1 — y)Т -дt ( ') п дi

д t

д Тпx

— и —п + д lC

Q • Т

С v ρ

+ K 1 • ( T c¹ + T — 2 Т п ) ,

д Т ‘

—— = w a t

- т + K 2 ( Т п — Т с¹ ) — Q ( Т п , Т с¹ ) , ^{д 1}

t е [ 0, Т ] ,     l е [ 0, L ]

д Tc²

д t

w -T c- + K 2 ( Т п — Т _с ² ) — Q ( Т „ , Т С ² ) ,

t е [ 0, Т ] ,     l е [ 0, L 1 ]

где р - массовая плотность смеси; t - время; и - скорость движения смеси, l - пространственная координата; x – концентрация горючего вещества в смеси (0 ≤ x ≤ 1); τ – время сгорания; R - газовая постоянная; q - теплота сгорания топлива; Tn - температура дымовых газов; Q(T) -потери тепла на излучение; (γ = 1 ÷ 1,4) – показатель адиабаты; Cv – теплоемкость газов при постоянном объеме; w – скорость сырья (нефтепродукта в радиантных трубопроводах печи); Ki - коэффициент теплопередачи для рабочего потока, TC, TC2 - температура нисходящего и восходящего потоков нагреваемого сырья соответственно; K2 - коэффициент теплопередачи для стенки печи; L – длина печи.

д р 3 /

д р - и ■ —

д l

д и

- c --, д l

д-Т=(1 - и)T-^ д t v n п д l

д x

9 t

ди д t

д и

- u ' д l

д T и--- + д I

x

д x x

9 I ^ф

„ д T n   RT n

R---- д l c

д р ’H

--q

Cv - Ф

Q-Tn  v It'

+ K. - T

Cv-c      1 ⁽ c

+ T 2 - 2 T ) ,

^{д T}c д t

-w- T + K2 .(T„ - Tc)-Q(T„, Tc), дTc2 - w дTc

_ w . _ ₊ K ² . T n _ T c ^)- Q T n , T c ) = 0.

Здесь x(l, t ) - концентрация горючего вещества, p( l, t ) , u ( l, t ) , T_n ( l, t ) - плотность, скорость и температура дымовых газов; T _c ( l, t ) , T_c ( l, t ) - температура нисходящего и восходящего потоков нагреваемого сырья; t, l – временная и пространственная координаты.

Начальные условия

X ( l ,0 ) = Ф 1 ( l ) ,   и ( ^{1 ,0} ) = ф 2 ( ¹ ) ,   T ( ^{1 ,0} ) = Ф з ( l ) ,   T c ( l ^,0 ) = ф 4 ( l ) .                 (3)

Граничные условия x (0, t) = ф, (t),  u (0,t) = Ф2 (t),  T (0, t) = Ф3 (t),  Tc (0, t) = Ф4 (t).                  (4)

Стационарную модель, которая следует из (1), исследуем более подробно:

d x x

"u "^7 — = 0, dl т

du

—U" —

—

д i

n д T R" —n

д i

—

RT„ др n

'i=°-

ρ

"

д u

—

д i

д Т U " —п +

д i

x

C v " т

—

Q" тп

C v "  P

+ K i " ( T C + T ²

—

2 Т п ) = 0,

w "

• ^д Т₊K 2 • ( Т п — Ty Q ( Т п , T C ) = 0.

• —w^Tc^ + K "(r — T— QТгп,T= 0. дi 2 ( п c ) V( "’ c )

Второе, пятое и шестое уравнения из (5) содержат пространственные производные только одной неизвестной функции. Приведем первое, третье и четвертое уравнения к виду, содержащему производную только от одной искомой функции dp / d l d u/ d l и d Т п / d l . Для этого применим теорию о неявных функциях к системе.

dp    дu „ u • —+ p--= 0, д1       < 1

(1 - Y )T,

д u

— д 1

д u      д T п   RT п dp_

U ---+ R ---1---- =

д l       д I     p д I

д T u •

0,

- ^Т ^+C7" ^ Tc+T‘"2Тп )=w, vv

В этом случае

др = Ai ди = а дтп =Аз д l А ’ д l А ’ д l А ’

где

А =

u

RТ п ρ0

ρ

u

R

— и ³ + y RuT п = и ( Y RT _п — и 2 )

u

ρ

u

ρ

^т =

u

R

= R рт, А 2 =

RТ п

u

R

τ

( 1 - Y ) ^Т п

—

u

ρ

τ

u

ρ

= R рт ,

Т =

п

RТ п

u

R

= и ² т.

ρ

τ

Таким образом, будем иметь:

др _ А1 _ Rcw

дl   А u ( yRTп - и2), ди _ А2 _     Ruw   _   Rw

да " Т _ " и (YRTп - и2) " YRTп - и2, дТп _ А3 _    и2w    _   uw дl А и ( yRTп - и2) YRTп - и2

Тем самым система (4) приведена к следующему виду:

R P I- x^q + Q - ЦТ ¹ + T ² - 2 Т_П )|

A p = ^H( C v т C v p ¹ ( c c       ^п ) J

AC           u (yRTп - u2)

u

V v ^T          v ^p

Y RT п - u 2

A u       V C v т      C v p     ^{1 (} c c ^п ) J

^A I               ^{Y RT} п ^- u

^T 8 1

= W ^{( T} п ^{- T} ' > " W ^Q < ^Tп^^ ■

5 T д i

K²- ( T п - T ² ) - 1 Q ( T п , T ² ) . ww

p ( 0 ) = a 1 ,    x ( 0 ) = a ₂ , u ( 0 ) = a ₃ ,

^Т п ( ⁰ ) = ^a 4 ,    T c ( 0 ) = « 5 , T c ( 0 ) = T c ( 0 ) .

Результаты численных исследований стационарных режимов

На рис. 2-5 отражены результаты расчетов стационарных режимов при различных начальных условиях для плотности р(l), концентрации x(l), скорости u(l) и температуры дымовых газов Тп(l). При этом за начальные условия приняты р(0) = 720 кг/м3, x(0) = 0,47, и(0) = 5 м/с, Тп (0) = 450 °C, T1 (L) = 270 °C. Затем начальные данные изменялись с шагом ± 5 % при постоян-c ных значениях остальных параметров.

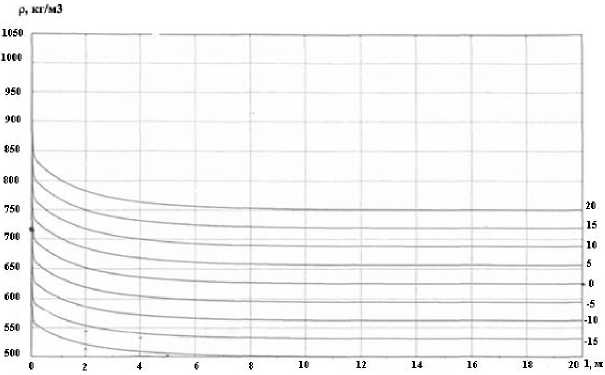
Рис. 2. Распределение плотности дымовых газов по длине объекта

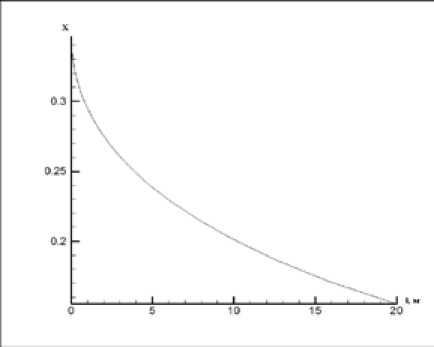
Рис. 3. Изменения концентрации горючего вещества

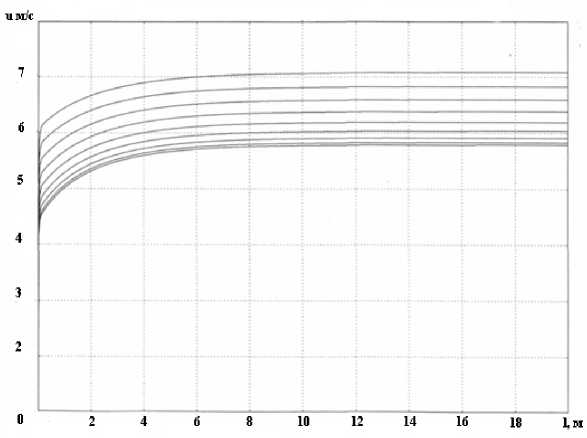
Рис. 4. Изменения скорости дымовых газов

Полученные результаты дают возможность сделать следующие заключения:

– увеличение плотности потока на выходе из печи происходит в силу снижения скорости потока газа и продуктов сгорания. На рис. 3 отражено выгорание топлива. При детальном рассмотрении процесса с помощью двумерных зависимостей [7] наблюдается оптимум в области температур вблизи 450 °С. Увеличение плотности потока выше оптимального приводит к увеличению недожога, снижению КПД процесса и увеличению количества вредных выбросов в окружающую среду. Снижение плотности характеризует недогрев сырья и, соответственно, неоптимальный режим работы технологической установки в целом;

• – выявлен эффект перераспределения теплообмена между потоком горячих газов и сырьем по длине печи (рис. 5), что может оказать влияние на качество получаемого про-

• Рис. 5. Изменения температуры дымовых газов

дукта, следовательно, изменяя температуру потока по длине печи или задавая режим работы, можно получать продукт заданного наперед качества;

• - управляя скоростью движения потока (рис. 4), имеется возможность регулировать плотность и, как следствие, величину недожога и, значит, количество выбросов в окружающую среду на выходе из печи.

Сопоставление полученных результатов со значениями управляющих параметров реального производства АНПЗ [7] показало хорошее соответствие (отличие составляет 1–5 %).

Вывод

Предлагаемый метод анализа стационарных режимов технологических печей позволяет еще на стации проектирования ректификационных установок обеспечить высокое качество разделения многокомпонентных смесей в нефтепереработке и нефтехимии.