Стандартная модель в ранней вселенной

Современная теория элементарных частиц и их взаимодействий — стандартная модель — с приемлемой точностью объясняет имеющиеся экспериментальные данные. Она была подтверждена открытием бозона Хиггса в экспериментах на Большом адронном коллайдере (далее — БАК). Стандартная модель представляет собой калибровочную теорию, в основе которой лежит группа симметрии SU (3) х SU (2) х U (1) , являющейся прямым произведением унитарных групп. Каждый множитель прямого произведения отвечает за определенный вид частиц и их взаимодействий. Сильные взаимодействия кварков описываются квантовой хромодинамикой с калибровочной группой SU (3) и характерной температурой 0 . 2 ГэВ. В электро-слабой модели с калибровочной группой SU (2) х U (1) группа SU (2) отвечает за слабые взаимодействия с характерной температурой 100 ГэВ, тогда как группа U (1) ассоциирована с дальнодействующими электромагнитны-

Standard Model in the early Universe

Institute of Physics and Mathematics,

Federal Research Centre Komi Science Centre, Ural Branch, RAS, Syktyvkar

A new hypothesis is put forward that the gauge group of the Standard Model becomes simpler with increasing temperature of the Universe, i.e. when moving back in time to the moment of its occurrence. It is assumed that this simplification is achieved by contracting the gauge group with the contraction parameter, which decreases with increasing temperature. In this case, the Lagrangian of the Standard Model is divided into terms that differ in powers of the contraction parameter. This makes it possible to arrange in time the stages of development of the Standard Model as the Universe cools. The evolution of the properties of elementary particles and their interactions, starting from the Planck scale of 10 19 GeV, is based on the explicit form of intermediate Lagrangians and explain the development of the Universe from simpler to more complicated structures - and not vice versa. The contraction hypothesis of the gauge group of the Standard Model contradicts the available experimental data on the Higgs boson production cross section.

Несмотря на наличие в теории большого количества свободных параметров [1], среди них нет параметра, связанного с температурой Вселенной и регулирующего порядок энергий, при которых стандартная модель адекватно описывает мир элементарных частиц и их взаимодействий. На заре ее формирования была выдвинута гипотеза [2, 3], получившая название теории великого объединения (далее — ТВО), согласно которой при некоторой большой энергии (температуре) Вселенной все три взаимодействия — сильное, слабое и электромагнитное — объединяются в одно гипотетическое взаимодействие в рамках более сложной калибровочной группы SU(5) или ей по- добных. Несмотря на обилие за последние полвека впечатляющих теоретических разработок, предсказания ТВО не подтвердились в современных экспериментах, в том числе в экспериментах на БАК [4].

Опираясь на значение характерных энергий, выдвинута [5–7] новая гипотеза: калибровочная группа стандартной модели становится проще с увеличением температуры Вселенной. Иными словами, по мере остывания Вселенной микромир эволюционирует естественным образом от простых структур к более сложным. В качестве механизма изменения калибровочной группы предложена операция контракции группы SU (3) х SU (2) х U (1) , параметр которой уменьшается при увеличении температуры . Поскольку средняя энергия (температура T ) горячей Вселенной связана с ее возрастом [8], то параметр контракции б ~ T -q , q >  0 стремится к нулю при T ^ ж , т.е. при приближении к моменту ее рождения в результате Большого взрыва.

Операция контракции (или предельного перехода) групп (алгебр) Ли давно известна в физике [9]. В результате предельного процесса исходная группа (алгебра) становится проще, часть коммутационных соотношений обращается в ноль, в частности, простая группа преобразуется в неполупростую. Позднее понятие контракции было распространено [10] на алгебраические структуры, такие как квантовые группы, алгебры Вирасоро, супергруппы и супералгебры Ли, а также на фундаментальные представления унитарных групп, которые имеют непосредственное отношение к стандартной модели. Для симметричной физической системы контракция группы симметрии означает переход к некоторому предельному состоянию системы. В случае сложной системы, каковой является стандартная модель, изучение ее предельных состояний при тех или иных предельных значениях физических параметров позволяет лучше понять поведение системы в целом. Мы обсудим на уровне классических калибровочных полей [11] модифицированную стандартную модель с контрактирован-ной калибровочной группой.

Деформация в широком смысле слова есть операция обратная к контракции. Нетривиальная деформация алгебраической структуры означает, вообще говоря, ее неочевидное обобщение и зачастую представляет собой значительное достижение в теории алгебраических структур. Ярким примером является открытие квантовых групп [12], т.е. таких обобщений алгебр Хопфа, которые являются одновременно некоммутативными и некокоммутативны-ми, тогда как ранее были известны алгебры Хопфа, обладающие только одним из этих свойств. Предложенным в этой классической работе методом построены квантовые аналоги простых групп (алгебр) Ли. Оказалось, что в случае полупростых групп (алгебр) метод не работает, поэтому квантовые аналоги этой категории групп (алгебр) Ли были получены методом контракций соответствующих простых групп (алгебр) [10]. Однако если сначала производится контракция некоторой математической структуры, то исходная структура может быть восстановлена с помощью деформации в узком смысле, выполняемой в обратном по отношению к контракции направлении.

Мы используем эту возможность для того, чтобы восстановить эволюцию частиц в ранней Вселенной, опираясь на достигнутый к настоящему времени уровень знаний. Для этого рассмотрим поведение стандартной модели в пределе «бесконечной» температуры, порожденное, в соответствии с нашей гипотезой, контракцией калибровочных групп SU (2) и SU (3) [5-7]. Подобные высокие температуры могут существовать в ранней Вселенной в первые мгновения после Большого взрыва [8].

Оказывается, что в результате контракции калибровочной группы лагранжиан стандартной модели распадается на ряд слагаемых, которые различаются степенями стремящегося к нулю контракционного параметра б ^ 0 . Поскольку температура в горячей Вселенной связана с ее возрастом, то, двигаясь вперед во времени, т.е. в обратном к высокотемпературной контракции направлении, мы заключаем, что после рождения Вселенной частицы и их взаимодействия проходят ряд стадий в эволюции от предельного состояния с «бесконечной» температурой до состояния, описываемого стандартной моделью. Эти стадии формирования кварк-глюонной плазмы, восстановления элек-трослабой и цветовой симметрий различаются по степеням контракционного параметра и, следовательно, по времени их возникновения.

Из контракции стандартной модели можно классифицировать указанные стадии по принципу «раньше–позже», но нельзя определить время, прошедшее после рождения Вселенной. Для установления абсолютного времени используем дополнительные предположения, а именно тот факт, что электрослабая эпоха начинается при характерной температуре 100 ГэВ, а эпоха квантовой хронодинамики (далее — КХД) при температуре 0 . 2 ГэВ. Иначе говоря, принимаем, что полная реконструкция электрослабой модели, лагранжиан которой включает слагаемые пропорциональные четвертой степени контракционного параметра ϵ , и восстановление КХД с минимальными слагаемыми в лагранжиане порядка восьмой степени параметра ϵ происходят при указанных температурах.

В рассматриваемом подходе расширяющаяся Вселенная является фоном, на котором развивается история частиц, а ее температура служит внешним параметром, обеспечивающим контракцию калибровочной группы стандартной модели. Более того, как будет показано далее, оценка «бесконечной» температуры 10 7 ГэВ меньше план-ковской энергии 10 19 ГэВ, при которой необходимо учитывать гравитационные эффекты. Таким образом, результирующая эволюция элементарных частиц не выходит за рамки проблем, описываемых электрослабым и сильным взаимодействиями.

Поскольку изменение калибровочной группы в процессе контракции происходит непрерывно, в том числе и в самом начале предельного перехода, можно попытаться уловить влияние эффекта контракции, сравнив полученные на БАК данные по сечению рождения бозона Хиггса при разных энергиях с теоретической зависимостью сечения от температуры Вселенной. Анализ доминантного механизма рождения и регистрации бозонов Хиггса на БАК в четырехлептонном процессе с точки зрения зависимости от температуры соответствующей диаграммы Фейнмана приводит к заключению о том, что гипотеза о контракции калибровочной группы стандартной модели как минимум не противоречит имеющимся экспериментальным данным по сечениям рождения бозонов Хиггса [13].

Калибровочная группа действует в пространстве полей, поэтому контракция калибровочной группы модели не затрагивает пространственно-временные переменные, от которых зависят поля. Следовательно, не меняется процедура квантования полей. Единственное изменение состоит в появлении той или иной степени контракционного параметра в качестве множителя перед амплитудой, отвечающей исходной фейнмановской диаграмме процесса.

1.    Электрослабая модель

Часть теории элементарных частиц, описывающая электромагнитные и слабые взаимодействия — электро-слабая модель — представляет собой калибровочную теорию с калибровочной группой SU(2) х U(1), действующей в пространстве C2 фундаментального представления группы SU(2). Векторы из C2 (или SU(2)-дублеты) опи- сывают три поколения лептонов:

где e есть электрон, µ — мюон и τ — лептон, ν _e , ν _µ , ν _τ — соответствующие нейтрино, а также три поколения кварков:

uct d, s, b.

Координаты векторов (или SU (2) -синглеты) представляют собой двухкомпонентные (или четырехкомпонентные, если учитывать античастицы) лорентцевы спиноры. В дальнейшем будем рассматривать только первые поколения лептонов и кварков. Электрослабая модель включает калибровочные бозоны, реализующие взаимодействия между частицами, а именно: переносчик электромагнитного взаимодействия фотон y , связанный с группой SU (1) , заряженные W ^± и нейтральный Z бозоны, ответственные за слабые взаимодействия, связанный с группой SU (2) . Имеется также специальная частица, ответственная в теории за появление массы у всех частиц — это бозон Хиггса χ . В полную теорию — стандартную модель — дополнительно включают глюоны A ^k , к = 1 ,..., 8 , которые переносят сильные взаимодействия. Глюоны связаны с группой SU (3) , действующей в пространстве C 3 цветовых кварковых состояний.

В этом разделе кратко опишем в нужном нам виде элек-трослабую модель, следуя монографии [11]. Лагранжиан модели, равный сумме бозонного, лептонного и кваркового лагранжианов L = L B + L L + L q , выбирается инвариантным относительно действия калибровочной группы SU (2) х U (1) в пространстве C 2 :

SU (2) : Z ‘ = Gz,

( Z1 W    в^г 1 У ia|2 + 1в 12 = 1, z2        -β αz

U(1) : Z‘ = егш/2Z = е^шУZ, ш € R.(1)

Генератор Y группы U (1) пропорционален единичной матрице Y = 2 1 . Генераторы группы SU (2)

Чей!       0 - ч -1

T1   2 V 0 )   2Т1 ,T2   2 \ i 0 )2

т - 41  0 А  1™

T3 2 У 0 -1 ) 2Т3 ’ где тк, к = 1,2, 3 есть матрицы Паули, удовлетворяющие коммутационным соотношениям

[ T 1 ,T 2 ] = iT 3 ,   [ T 3 ,T 1 ] = iT 2 , [ T 2 ,T 3 ]= iT 1 (3)

и образующие алгебру Ли su (2) .

Бозонный сектор L B = L W + L ^ состоит из двух частей: лагранжиана калибровочных полей

L w = - 4[( W ^v ) ² +( W 2V ) ² +( W ³v ) ² ] - 4( B , ) ² , (4) и лагранжиана полей материи

L 3 = |( D , * ) ' D , ^{ф -} 4 ( Ф ^ Ф ^- v 2 ),

• * = ( Ф2 ) € C2.

Ковариантные производные равны

D^* = д^ф - ig (yT Tk wA ф - ig’YB^*,(6)

k =1

где константы g и g′ являются зарядами. Калибровочные поля

W, (x ) = y Tk Wk (x), B, (x)

k =1

принимают значения в алгебрах Ли su (2) , u (1) соответственно, а их тензоры напряженности определяются формулами

W ,v ( x ) = W ,v ( x ) + g [ W , ( x ) , W v ( x )] ,

W kv ( x ) = dW ( x ) - d v W^' ( x ) ,

B ,v ( x ) = B ,v ( x ) = d , B v ( x ) - d v B , ( x ) .    (8)

Вместо полей (7) вводятся новые калибровочные поля

Z , ^{( x} ) = / 21.     (gW »^{( x} ) ^{- gB} , ^{( x} )) ,

V g ² + g ‘ ²

A , ^{( x} ) = / ₂¹,     (g ‘ ^W _ц ^{3 ( x} )⁺ gB , ^{( x} )) ,

V g ² + g' ²

^W ±± ⁽ x ) = v 12 ( W ¹ ' x ) ^: i^{W ц} 2 ⁽ x )) ’        ⁽⁹⁾

имеющие непосредственный физический смысл.

Для генерации масс векторных бозонов вводится специальный механизм спонтанного нарушения симметрии. Одно из основных состояний лагранжиана LB фуас = -L ( 0 Y Wk= = B, = 0 ,k = 1, 2, 3, (10)

где v = const , выбирается в качестве вакуума модели, и затем рассматриваются малые возбуждения полей ^ 2 v + х ( x ) относительно этого вакуума.

После спонтанного нарушения симметрии бозонный лагранжиан (4), (5) принимает вид

Г „ — Т ⁽²⁾ I Tint _ LB = LB ⁺ LB =

• = 2 ( ^д ^ ^{х ) 2} - 2 m X ^{х 2} - 4 Z ^v Z ^v ⁺ 2 m Z ^Z v ^Z v ^-

• - 4 F .v F .v - 2 WW -v + m W W + W - + L . t , (11)

^где F v v ⁽ x )       ^д v ^A v ⁽ x )     ^д v A v ⁽ x ) , Z vv ⁽ x )

d _M Z v ( x ) - d v Z v ( x ) , W ±vv ( X ) = d v W ± ( x ) -д _v W ± ( x ) • Как обычно, слагаемые второго порядка описывают бозонные частицы модели, а слагаемые более высокого порядка L ⁱ _B ^nt рассматриваются как взаимодействия частиц. Таким образом, лагранжиан (11) вк лючает скалярный бозон Хиггса х с массой m _X = V2 Av , нейтральный Z бозон с массой m _Z = 2 1/ g ² + g' ² , безмассовый фотон A и заряженные W ^± бозоны с одинаковыми массами m W = 2 gv . Все эти частицы экспериментально обнаружены и имеют следующие массы: m W = 80 ГэВ, m _Z = 91 ГэВ, m _X = 125 ГэВ.

Лагранжиан LiBnt, описывающий взаимодействия частиц, имеет вид т int _ gmz / 7 .2    .   3. g2 У2 2

L B = 2^ 9 W^{( Z v} ) ^{X-х +}8cos 2 9w ^{( Z v} ) ^х -

• - 4 X ⁴ - 2 W v W -v + m W W. " W -" "

• - 2 ig ( W ^ + W - - W -^- W + ) ( F vv sin 9 w +

+ Z vv cos 9 w ) - ie [ A v ( W ; W - - W-_vW + ) -

-A v ( W, v W -^- - W -v W, " )] +

-VqW ⁺ W \- — cos 9_W \Z„ fW⁺ W   W IT ' )

• ¹    g ^{v v} v * ^X A, 2 W L v V ^v v v v    * ^v v v v /

  -Z v ( w + W -- -W -v W, ")] +

+ g _ (V+ w- - w TV⁺)² + — w⁺ w- y² —

• ¹    4 v v v ^r v v /    ¹  4 *^r v v ^X

• - J {[( ^W. + ) ² + ( ^W -- ) ² ] ( A v ) ² -

• - 2 ( W^ ⁺ W v ⁺ + W -^- W - ) A v A v +

• + [( W"    + ( W- ) ² ] ( A v ) ² } -

• -g ² cos 9 w {[( W, ⁺ ) ² + ( W- ^- ) ² ] ( Z v ) ² -

• -2 (W^+ W+ + W--W-) ZvZv+

+ [( W + ) ² + ( W - ) ² ] ( Z v ) ² } -

• -eg cos 9w | W ,⁺ W -^- A v Z v + W + W - A^Z ^. -

• -2 (W,+ W- + Wv+ W--) (AvZv + AvZv)}•  (12)

Фермионный сектор включает в себя лептонный L L и кварковый L Q лагранжианы. Для первого поколения лептонный лагранжиан выбирается в виде

L l = L ^ iT^ v D v L i + е Г ir v D v e r -

-h e [ ^е Г ⁽ ф^ L l ) ^{+ (} L ^ ^ ) e r ] ,             ⁽¹³⁾

где L l

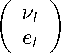
есть SU(2)-дублет, поле правого элек трона er — SU(2)-синглет, he — константа связи Юка- вы, т0 = 70 = 1, 70 = -rk — матрицы Паули, er , el , νl — двухкомпонентные лорентцевы спиноры. (Мы ограничиваемся рассмотрением только частиц. Для учета античастиц поля должны быть четырехкомпонентными биспинорами Дирака.) Поле ф выбирается в виде ф = ^ v *+ х ^, а Dv обозначают ковариантные производные левых и правых лептонных полей

D v L i = д v L i - i^= ( W _ц ⁺ T ₊ + W - T - ) L i --i^rZ v ^Г з - Q sin ² 9w^ L i - ieA v QL i , cos 9_w    ^v               '

Dver = д ver - ig'QA ver cos 9w + ig'QZ ver sin 9w, где Г± = Г1 ± iT2, Q = Y + Г3 есть генератор электромагнитной подгруппы U(1)em, Y = 21 — гиперзаряд, e = 99*(g2+g'2)-2 —заряд электрона и sin 9w = eg-1 •

Согласно современным воззрениям, все известные лептоны и кварки образуют три поколения. Следующие два поколения лептонов вводятся аналогично (13). Они являются левыми S U (2) -дублетами

( ^Vv ),   ( ^Vt ) , Y = - ¹        (15)

V ^ Л ^т Л 2

и правыми SU (2) -синглетами: ц _г , т _г , Y = - 1 • Помимо и и d кварков первого поколения существуют кварки ( c, s ) и ( t, b ) следующих поколений, левые поля которых

( c ⁱ У  f t ⁱ У   Y = 1         (16)

V si )    \bi J ’        6

описываются S U (2) -дублетами, а правые поля являются SU (2) -синглетами: c r , t r , Y = 3 ; s r , b _r , Y = - 3 . Лагранжианы всех поколений кварков вводятся единообразно по правилу лагранжианов лептонов. Полные лептонные и кварковые лагранжианы получаются суммированием по всем поколениям. В дальнейшем мы будем обсуждать только первые поколения лептонов и кварков.

В терминах полей электронов и нейтрино лептонный лагранжиан (13) записывается в виде

L l = e ^ iT v д v e i + e r ir v d v e r -

-m e ( e r e i + e ^ e r ) - h e х ( e r e i + e^ r ) +

. g ^{cos2 9}w t^       t- Л              t Л

+ ---7— V T v Z v V i + ev T v A v v i + g cos 9 w e ^ T v A v e r -

• 2 cos 9 _w               ⁱ

  -g' sin 9 w e \ т v Z v e r + v \ iT v д v V i -

• g

2 cos 9 _w

e^ v Z v e i +

⁺ "  ^^{/7 w w} + e l + e^ W - v^ ,      (17)

где m e = h e ²v2 — масса электрона в хиггсовском вакууме.

Кварковый лагранжиан строится аналогично лептонному лагранжиану

^-h d ^[ d r ( Ф ^ ^Q l ) ⁺ ( Q^ ) d r ^] -

—h u [ u r ( ф ^Qi ) + ( Q ^) U r ] ,           (18)

u l d l

где левые кварковые поля образуют SU(2)-дублет Qi = , правые поля ur,dr являются SU(2)-синглета- ми, фi = eikфк ,e00 = 1, eii = — 1 образуют сопряженное представление группы SU(2), hu, hd есть юкавские константы связи. Для частиц все поля ul , dl , ur , dr являются двухкомпонентными лорентцевыми спинорами. Ковариантные производные кварковых полей равны д. — igT?k wk — k=1

ig ' 6 B .

Q l ,

• 2.    Электрослабая модель при высоких энергиях

Известно два способа описать действие контрактиро-ванной группы в пространстве с вырожденной метрикой. Традиционный способ заключается в рассмотрении действия матричной группы с вещественными или комплексными элементами на векторы с такими же компонентами z1′            α

V z V —e

_ϵ 2 _β a

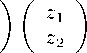
det u ( e ) = |a| ² + e ² |в| ² = 1 , u ( e ) u ^r ( e ) = 1 , lz 1 1 ² + e ² |z 2 1 ² = inv.                 (21)

В пределе e ^ 0 матрица имеет вид

u(0) = f —“в ° ) ’ a = ei7 ’ Y ^ R и очевидно принадлежит евклидовой группе E(2).

Другой способ состоит в рассмотрении контрактиро-ванной группы SU (2; e ) и соответствующего пространства C ₂ ( e ) путем согласованного переопределения элементов группы SU (2) и компонент векторов пространства С ₂ ви-

D u r

= д

-

ig ' | B .

u r ,

да

( ^z 1 ^ = ^ “-

ϵz ₂ ^′          -ϵβ

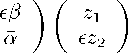
D d

r = д

⁺ ig ' | B .

d r ^.

det u ( e ) = |a| ² + e ² |в| ² = 1 , u ( e ) u ^r ( e ) = 1 , lz 1 1 ² + e ² |z 2 1 ² = inv.                 (22)

Кварковый лагранжиан (18) в терминах полей u и d кварков можно записать в виде

—h u X ( " r u i + u ^f u r ) +

⁺ ^2 cos ⁶ w ^—

⁺ " И ^T . ^W + d i ⁺ d '^ ^W - ^u i ] ⁺

+ | g ' cos 6 w u r t^uu, — | g ' sin 6 w u rT-. Z . u r , (20)

где m u = h u-v2 , m d = h d-v2 обозначают массы u и d кварков в хиггсовском вакууме.

Наш подход основан на действии матриц с элементами, зависящими от параметра контракции ϵ , на векторы, компоненты которых также зависят от этого параметра. В этом случае при e ^ 0 необходимо дополнительно учитывать бесконечно малые соотношения первого порядка по ϵ . Стремящийся к нулю контракционный параметр удобен для физических приложений, но его использование в форме (22) вызывает иллюзию исчезновения ряда групповых параметров. Математически этого можно избежать, приняв параметр равным нильпотентной единице ι , которая сама отлична от нуля i = 0 , но ее квадрат обращается в нуль 1 ² = 0 . Тогда контрактированная матрица

α ιβ u (1) = ( —1в “ J ’

a = e ii , y 6 R

будет явно содержать все параметры группы, но часть из них будет нильпотентными элементами. Этот подход детально рассмотрен в работе [10].

После перехода к пределу e ^ 0 группа SU(2; e = 0) становится изоморфной евклидовой группе E(2), а пространство C2(e = 0) разбивается на базу, натянутую на координату {z1 }, и слой, порождаемый координатой {z2}. (Широко известное нерелятивистское пространство–время является примером расслоенного пространства с одномерной базой, физически интерпретируемой как ось времени, и трехмерным слоем, рассматриваемым как абсолютное собственно пространство.) Унитарная группа U(1) и ее действие в пространстве C2(e = 0) не изменяются при контракции и описываются формулами (1).

Пространство C ₂ ( e ) получается из С ₂ заменой z ₂ на ϵz 2 . Замена матричного элемента β на ϵβ индуцирует замену генераторов алгебры Ли T 1 → ϵT 1 , T 2 → ϵT 2 , T 3 → T 3 . Эти новые генераторы подчиняются коммутационным соотношениям

[ T 1 ,T 2 ] = ie ² T 3 , [ T 3 ,T 1 ] = iT 2 , [ T 2 ,T 3 ] = iT 1 (23)

алгебры Ли su (2; e ) , которая при e = 0 представляет собой полупрямую сумму абелевой подалгебры t ₂ = {T 1 ,T ₂ } и одномерной подалгебры и (1) = {T 3 } : su (2; e = 0) = t ₂ 3 3 и (1) .

Поскольку калибровочные поля принимают значения в алгебре Ли, можно вместо преобразования генераторов произвести замену калибровочных полей, а именно:

W µ ¹ → ϵW µ ¹ ,  W µ ² → ϵW µ ² ,

W µ ³ → W µ ³ ,  B µ → B µ .         (24)

Действительно, из свойств коммутативности и ассоциативности умножения на скаляр имеем su(2; e) Э { W^eT1) + W2(eT2) + W^T3} =

= {( eW ^ ) T 1 + ( eW 2 )T 2 + W ^ T 3} . (25) Подстановка β → ϵβ индуцирует преобразование стандартных калибровочных полей (9) вида

W µ^± → ϵW µ^± , Z µ → Z µ , A µ → A µ . (26)

Левые лептонные L l

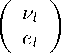
и кварковые Q l =

u l d l

поля являются SU(2)-дублетами, поэтому их ле- вые и правые компоненты преобразуются так же, как ком- поненты вектора z, а именно:

e l → ϵe l , e _r → ϵe _r , d l → ϵd l ,   d _r → ϵd _r ,

ν _l → ν _l , u _l → u _l u _r → u _r .         (27)

Отдельно от групповой структуры вводится специальный механизм спонтанного нарушения симметрии, который используется для генерации масс векторных бозонов и других частиц модели. В этом механизме одно из основных состояний (10) лагранжиана L B выбирается в качестве вакуума модели и затем рассматриваются малые возбуждения относительно второй компоненты вакуумного вектора. При этом поле бозона Хиггса χ , константа v , а также зависящие от v массы частиц на параметр контракции не умножаются. В результате преобразований полей бозонный лагранжиан можно записать в виде

L B ^{( e} ) = L B, 0 ^{+ e 2} L B, 2 ⁺ L Bt ^{+ e 2} L Bt ^{+ e} 4 L Bt , ⁽²⁸⁾

L b, 2 = — 2 W ⁺ v W -v + m W W, " W - ,    (30)

L Bt = - 4 ^{x 4 - Xvx 3 +} ₂ g^Q ^{x ( Z} i ^{) 2 +} 4            2 COS v w

+ _R ⁹ L x ² ( Z i ) ² ,             (31)

8 cos2 9w int         + - g2 2 + -

B, 2     ^9xvv i ^vv p ¹ 4 ^{x vv} i ^vv и

• - 2 ig ( W ^ ⁺ W ^- - W -^- W , ) ( F iv sin 9 w + Z ^_v cos 9 w ) -

• -    ie [ Ai (W+ W- -W-v Wv+) - - Av (W+vW-- - W-vW,")] -

  - ig cos 9w [Zi (WvW- - W-vW+) -

• - Zv (W+vW-- - W-vW1+)] -
• -    4 {[( W.+ ) + ( W-- ) ] ( Av )2 - - 2 (Wi+ W+ + W--W-) AiAv+

+ [( W +) ² + ( W - ) ² ] ( A i ) ² } -

• -g ² cos 9 w {[( Wi ⁺ ) ² + ( W- ^- ) ² ] ( Z v ) ² -

• - 2 ( Wi ⁺ W + + W -^- W - ) Z i Z v +

+ [( w + ) ² + ( W - ) ² ] ( Z i ) ² } -

• -eg cos 9w [w„ ⁺ W -^- A v Z v + W , W - A^ i -

  - 2 (W1+ W- + W+ W--) (AiZv + AvZi) ,(32)

lb,4 = 94- (wm+ w- - w--w+) .(33)

Лептонный лагранжиан (13), (17) в терминах полей электронов и нейтрино принимает вид

Ll (e) = Ll, 0 + LiLno + e 2( Ll, 2 + L^2),(34)

где

Ll, 0 = v ^ iT i d i V i ,

+   -        9 cos 2 9 _w * „

L_Tn = eViT„A_uvi +--- —v,t_u Z„vi,

L, ⁰       l ^{i i} l ⁺ 2cos 9 _w l ^{i i} l ,

L l, 2 = e * iT i d^i + e ^ iT i d^r --m e ( e r e i + e ^ e r ) - h e x ( e r e i + e * e r ) ,

где

L B, 0 = - 4 F iv - 4 Z iv ⁺ 2 m Z ⁽ Z i ) ⁺

■ 2^{( d} i x ^{) 2} — 2 m X x ² ,             ⁽²⁹⁾

int

L L, 2 =

-

g

2 cos 9 _w

e * T i Z^ i +

+ 9 ' cos 9 w e r T i A^ r - 9 ’ sin 9 w e r T i Z^r +

⁺ v⁹ ^ ( ^i WW ⁺ e i ⁺ e^i W -- V ) .      ⁽³⁸⁾

Кварковый лагранжиан (18), (20) в терминах полей u и d кварков записывается в виде

3. Квантовая хромодинамика

L Q ^{( 6} ) — L Q, 0 ^{+ 6} 2 L Q, 2 ⁺ L Qt ^{+ 6 2} L Qt ,    ⁽³⁹⁾

где

L q, о — Tt ц д ^ и + u r iTд u . -

-m u ( u r u i + u ^ U r ) - h u X(u r u i + u ^ u . ) ,     (40)

L n ^— y u^A M u i ⁺

+

( 2 cos 9 w -

g

— Sin 9 w

u ^ T ^ Z ^ u i +

2 ,     „ + „

Сильные взаимодействия частиц описываются квантовой хромодинамикой, которая является калибровочной теорией, основанной на локальных цветовых степенях свободы кварков [1]. Калибровочная группа SU(3) КХД действует в трехмерном комплексном пространстве C3 цве- q1 qR товых кварковых состояний q — q2 = qG 6 q3 qB

C ₃ , где q ( x ) есть поля кварков q — u,d,s,c,b,t , а R (красный), G (зеленый), B (голубой) обозначают цветовые степени свободы. Калибровочные бозоны группы SU (3) называются глюонами. Всего имеется восемь разных глюонов, обмен которыми обеспечивает сильные взаимодействия кварков. Лагранжиан КХД выбирается в виде

L q , 2 — dU^d ^ d i + d r iT^d r -

L — ^2 ( q i ( iY ^Ц )( D ^ ) ij q j - m q S i q ^ ) - ^q

-m d ( d r d i + d ^ d r ) - h d X ( d r d i + dd ) ,   (42)

-

L int ^{— -} (2^COS ^ w ⁺ ^ ^Sin ^ w) d ^ ^T ^ Z ^ d i ⁺

4 F L f ^v f ^^va ,

⁺ У^ 2 u ^U ‘ ^T ^ W + d i ^{+ d} i ^T ^ ^W M ui) -

-ld l T _M A _M d i - | g ' cos 9 w d r r ^ A ^ d r +

+| g ' sin 6 w d r r ^ Z ^ d r .            (43)

Полный лагранжиан электрослабой модели с контрак-тированной калибровочной группой получается суммированием бозонного, лептонного и кваркового лагранжианов и представляется в виде разложения по степеням контракционного параметра

L ewm ( 6 ) — L ( 6 ) + L int ( 6 ) —

— L о + 6 ² L 2 + Lf n + 6 ² Lf n + 6 ⁴ L 4 ,    (44)

где

^L 0 ^— LB, 0 ⁺ LL, 0 ⁺ LQ, 0 ,

int int int int

^L 0   ^{— L} B 0 ^{+ L} L 0 ^{+ L} Q 0 ^,

L 2 ^— L B 2 + L L 2 + L Q 2 ^, int int int int int int ^L 2   ^{— L} B 2 ^{+ L} L 2 ^{+ L} Q 2 ^{,  L} 4   ^{— L} B 4 ^.

Мы предполагаем, что параметр контракции является монотонной функцией 6 ( T ) — AT ^-q , q> 0 температуры (средней энергии) Вселенной со свойством 6 ( T ) ^ 0 при T ^ ж . Когда 6 ^ 0 , слагаемые с более высокими степенями ϵ вносят меньший вклад в лагранжиан по сравнению со слагаемыми с меньшими степенями. Таким образом, электрослабая модель демонстрирует три стадии поведения при движении назад во времени к моменту рождения Вселенной, которые отличаются степенями контракционного параметра.

где D _µ q есть ковариантные производные кварковых полей

D . q — д ^а - - igs ( it) aO) q. (47)

Здесь g _s обозначает сильную константу связи, t a — X a / 2 — это генераторы группы SU (3) , X a есть матрицы Гелл-Манна

/ 0 10 \        / 0 -i 0 \

X1 —10 0  , X2 — i 0 0

/ 10  0 \        / 0 0 1

X3 —    0  -1 0   ,  X4 —    0  0  0

\ 0 0   0 /          \ 1  0  0/

/ 0 0  -i \          / 0  0  0

X5 —    0  0 0    ,   X6 —    0  0  1

i00010

/ 0 0  0 \         1  / 10  0

X7 —   0  0  -i   ,  X8 — —=   0 1   0

\ 0  i   0 У         V3 у 0 0  - 2У

Глюонный тензор напряженности имеет стандартный вид

Fa — d.Aa - dvAa+gs/aeY ^^г,(49)

где f “^eY есть структурные постоянные алгебры su (3) : [ t ^a , t ^e ] — if ^aeY t ^Y , a, в, Y — 1 ,..., 8 . Они антисимметричны по всем индексам, а их ненулевые значения таковы:

f 123 _— 1    f 147 _— f 246 _— f 257 _— f 345 _— ¹

_f 156

— f ³⁶⁷ —

2 ’

_f 458

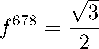
Выбор матриц Гелл-Манна в виде (48) фиксирует базис в алгебре su (3) , что дает возможность выписать ковариантные производные (47) в явной форме

Dt = I д^- gs i

A t + т з A t I A t + iAI \ A t + iA t

A ¹ µ - iA ² µ √ ¹ ₃ A ⁸ µ -A ³ µ A t + iA t

= I д _ц

g s i

RR   RG

A _µ    A _µ

GR   GG

A _µ    A _µ

_{A µ}BR _{A µ}BG

A ⁴ µ - iA ⁵ µ

A t - iA t I =

3 ^µ

^µ _{A µ}GB _{A µ}BB

где

RR

A t

8     3 GG         8     3

^— 3 A t ⁺ A t ,  A t     ^ з A t   A t ,

A

BB µ

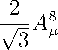
A RR + A GG + A BB = 0 , µµµ

A GR = A t + iA t = A RG , A BR = A t + iA t = A RB , A B^G = A t + iA t = A '. Лагранжиан (46) принимает вид

L = ( u i ( iY ^t )( D t ) ij U j ~ m u U i u i )+ ... — J F a F ^tv“ =

= L u + ... - J F Bv F ^tva ,         (53)

где выписаны только слагаемые, характеризующие u кварк. Отметим, что в КХД отсутствует механизм спонтанного нарушения симметрии, поэтому глюоны являются безмассовыми частицами.

Лагранжиан КХД имеет богатое динамическое содержание. Он описывает сложный спектр адронов, цветовой конфайнмент кварков, асимптотическую свободу и много других эффектов.

4. КХД с контрактированной калибровочной группой

В данном разделе будем рассматривать только два вида кварков q = u,d и учитывать преобразования (27). Контрактированная специальная унитарная группа SU(3; б) определяется согласованным действием мат- ричного элемента группы на вектор в цветовом пространстве C3(б)

q (б) = U (б) q (б), q1′              u11    ϵu12 ϵ2u13         q1

бq 2 I = I    би 21    U 22    би 23    II    бq 2 I

ϵ ² q ₃ ^′             ϵ ² u 31 ϵu 32 u 33          ϵ ² q 3

при б ^ 0, где q 1 = u 1, бd 1, q2 = u2, бd2 , qз = uз , бdз. При таком действии остаются инвариантными предельные эрмитовы формы ut (б)и(б) = |u 1|2 + б2 |и2 |2 + б4 |и3 |2 , dt (б)d(б) = Id 1|2 + б2 Id2|2 + б4 Idз|2 .      (55)

Переход от классической группы SU(3) и пространства С3 к группе SU(3; б) и пространству C3(б) достигается преобразованием калибровочных полей (52) и цветовых компонент кварков вида u1 → u1 , u2 → ϵu2, u3 → ϵ2u3, d1 → ϵd1 , d2 → ϵ2d2 , d3 → ϵ3d3,

GR GR BG     BG BR 2 BR

A _µ → ϵA _µ , A _µ → ϵA _µ , A _µ → ϵ A _µ . (56) При этом диагональные калибровочные поля A _µ ^RR , A _µ ^GG , A _µ ^BB не изменяются.

Подстановки (27), (56) приводят к следующему разложению кварковой части лагранжиана КХД по степеням контракционного параметра

L q ( б ) = L q ( б )+ L n ( б ) =

= ^б2k (Lq,2k + Lqnk) ,(57)

k =0

где

L q, 0 = L u, 0 , L q, 2 = L u, 2 ^{+ L} d, 0 ,

Lq,4 = Lu,4 + Ld,2 ,   Lq,6 = Ld,4 ■

Здесь

Lu,0 = iU1 YtdtU 1 - mu |u 11 ,(59)

Lun0 = + gs Iu 112 Yt (—At + At) ,(60)

Lu,2 = uY^u2 - mu |u2|2 ,(61)

Lint = gs |u212 Yt ( 1-A8 - A3) + u, 2      2 12 1 1 I /3 t t )

^{+ u} 1 u 2 Y ^t ( A t ⁺ iA t ) ^{+ u} 1 ^u 2 Y ^t ( A t ^- iA t ) j , ⁽⁶²⁾

Lu,4 = iu3Ytdtu3 - mu |uз12 ,(63)

L un, 4 = g s [^_ ;23 |u 3 1 ² Y ^t A t +

^{+ u} 1 ^u 3 Y ^t ( A t ⁺ iA t ) ^{+ u} 1 ^u 3 Y ^t ( A t ^- iA t ) ⁺

+ u 2 u 3 Y ^t ( A t + iA t ) + u 2 u 3 y ^t ( A t - iA t ) ] . (64)

Слагаемые L d, _{2 k} , L dn2>_k , k = 0 , 1 , 2 описываются формулами (60)-(64) с заменой u p на d p , p = 1 , 2 , 3 .

Глюонная часть L gl = - 4 F B^_V F ^tva лагранжиана приобретает вид

(0)     2 (2)     4 (4)     6 (6)     8 (8)

L gl ^{( б} ) = L gl ^{+ б} L gl ^{+ б} L gl ^{+ б} L gl ^{+ б} L gl , ⁽⁶⁵⁾ где

L g0 ⁾= - 4 {( ^d t A v - ^d v A t )⁺ ( ^d t A v - ^d v A t )} ,

Г(2) — а д ¹ _ а д ¹      (д² д³ — д³ д²^

L gl = 4 1 ^d ° A V ^- ° v A 7 ⁺ g s WAV A 7 A v) I ⁺

⁺ ( Э ^ А V - Э „ A 7 + 2- [( A 7 A V - A 7 A) ) +

+ V s ( А;А8 - А7A 7)]) +

⁺ ( ^d 7 ^AV — ^d V ^А 7 ^— g s ( A 7 A V ^- A 7 ^А V )) ⁺

⁺( ^д 7 ^А V ^{- А}A 7 ^- у [ A 7 A V ^- A 7 A V ⁺

+ V 3 ( А 7 А V - А 7 А V )])2+

⁺ g s (2 ( A 7 A V - A 7 A V ) ^-

^-А 7 A V ⁺ A 7 A V ) ( ^д 7 ^А 7 ^{- d} v A 7 )⁺

+V3 (А7АV - А7АV) д АV - dvА7)1 I,(67)

L (4) = - 4^ (д7А V - dv A 7 ) + (д7А V - dv A 7 )

47  74  56  65    11

⁺ g s I A 7 A v A 7 A V A 7 A V ⁺ A 7 A V I Аа:<  U y . 7) ⁺

+2 (А 7А V - А 7А V + V3 (А 7А V - А 7А V )) х х (A7А V- А 7AV- А 7А V+ A 7A V)-

• ^- ^ ( A 7 A V ^- A 7 A V ⁺ V ³ ( A 7 ^А V ^- A 7 A V )) ^х

14   41     5   5

^х ( A 7 A v ^A 7 ^A v ^{+ A} 7 ^A v ^A 7 ^A v j ⁺

17   71     6   6

⁺ 2 y A 7 A v ^A 7 ^A v ^{+ А} 7 A v   ^A 7 ^A v ⁺

+ А 7 А V - А 7 А 7 - ^V 3 ( А 7 А 7 - А 7 А ⁾ )) 2 +

• +2 ( А7А7 - АТ.А.7 - А7А7 + А7^₁А7 +

+ А 7 А 7 - А 7 А 7 - ^V ( А 7 А 7 - А 7 А ) )) 2 ] у (68)

• (6)        g s       4 7      7 4      5 6      6 5

L gl = 16 1 \ ^A 7 ^A v ^A 7 ^A v ^A 7 ^A v ^{+ А} 7 ^А р) ⁺

• +    ( А 7 А 7 - А 7 А7 + А 7 А 7 - А 7 А V ) ² +

• +    ( А 7 А 7 - А 7 А 7 - А 7 А7 + А 7 А ) ) 2 +

• +    ( А 7 А 7 - А 7 А7 + А 7 А 7 - А 7 А 7 ) 2 +

46  64  57  75    2    2

• ⁺    ^ ^A 7 ^A v ^A 7 ^A v ^{+ A} 7 ^A v ^А 7 ^А р^ ^д 7 ^А^_у O _v ^А 7^

• -    ( А 7 А 7 - А 7 А7 + А 7 А 7 - А 7 А 7 + А 37 А 7 - А 7 А 7 -

• -V3 (А 7А 7- А 7А V)) (д7А 7- dvА 7)+

+ ( А 7 А 7 - А 7. А 7 - А 7 А7 + А 7 А 7 + А 37 А 7 - А 7 А 7 -

• -V ³ ( ^А 7 ^А 7^{- А} 7 ^А) )) ( ^д 7 ^А V ^{- d} v ^А 7 )⁺

4   4     15   51     6     6

• ⁺    1 ^А 7 ^А ^ ^А 7 ^А у ^А 7 ^А у ^{+ А} 7 ^А у1 У ^А^ Л-у U y ^А 7) ⁺

14   41     5   5        7     7

• ⁺    1 ^А 7 ^А ^ ^А 7 ^А у ^{+ А} 7 ^А у ^А 7 ^А у1 У ^А^Л-у U y ^А 7) ⁺

• ⁺ V ³ ( ^А 7 ^А 7 - ^А 7 ^А) ) ( ^д 7 ^А V ^{- d} v ^А 7 /|⁺

• ⁺ g s [( ^А 7 ^А7 - ^А 7 ^А) ) ⁺ ( ^А 7 ^А V ^{- А} 7 ^А) ) ^-

• - (А7А7 - А7АV) (А7А7 - А7а)) -

  13  31  46  64  5775

I ^A 7 ^A v ^A 7 ^A v) 7 ^A 7 ^A v ^A 7 ^A v ^{+ A} 7 ^A v ^A 7 ^A v) ⁺

3   3    47  74  5665

• ⁺ ( ^A 7 ^A v ^A 7 ^A v) 7 ^A 7 ^A v ^A 7 ^A v ^A 7 ^A v ⁺ A 7 Av) ⁺

⁺⁴( ^A 7 ^A V ^{- A} 7 ^A 7 ⁺ A 7 ^AI - A 7 ^A V ) ( A 7 ^A V

(8)       gs2    4 55 4

L gl =   4 ( A 7 A V    A 7 Av) .

- А ⁵ ₇ А ^{4 )} ,

В результате объединения (57) и (65) лагранжиан модифицированной КХД может быть представлен в виде разложения по степеням контракционного параметра

L qcd ( e ) = L q ( 6 ) + L qn ( e ) + L gl ( e ) =

= L ⁽⁰⁾ + e ² L ⁽²⁾ + e ⁴ L ⁽⁴⁾ + e ⁶ L ⁽⁶⁾ + e ⁸ L ⁽⁸⁾ ,    (71)

L (0) = L uo + L Un 0 + L (0 > ,  L ⁽⁸⁾ = L (8) ,

^L (2 p) = L u, 2 p ⁺ L d, 2( p- 1) ⁺ L u, 7_p ⁺ L d, 2 ( p- 1) ⁺

+ L ⁽2^p) , p =1 , 2 , 3 . (72)

В соответствии с нашей гипотезой контракционный параметр является монотонной функцией температуры e ^ 0 при T ^ го . Согласно современной концепции возникновения Вселенной [8], очень высокие («бесконечные») температуры могут существовать на первых стадиях Большого взрыва сразу после инфляции в доэлектрослабую эпоху.

5.    Оценка границ между эпохами в эволюции Вселенной

Объединяя лагранжианы электрослабой модели (44) и вантовой хромодинамики (71), получаем лагранжиан стандартной модели, представленный в виде разложения по степеням контракционного параметра

L sm ( 6 ) = L ewm ( 6 ) + L qcd ( 6 ) =

= L ( 6 ) + L q ( 6 ) + L in ( 6 ) + L n ( 6 ) + L gi ( 6 ) =

= L о + 6 ² L 2 + 6 ⁴ L 4 + 6 ⁶ L 6 + 6 ⁸ L 8 ,     (73)

где с учетом выражений (45) и (72) имеем

L p = L p + L n + L (^p ) , p = 0 , 2 , 4 ,

L 6 = L ⁽⁶⁾ , L 8 = L ⁽⁸⁾ .            (74)

Таким образом, в зависимости от степени контракционного параметра стандартная модель демонстрирует пять стадий поведения при движении назад во времени к моменту рождения Вселенной. Как уже отмечалось, контракция калибровочной группы стандартной модели обеспечивает возможность упорядочить во времени различные стадии развития Вселенной, но не позволяет определить абсолютные даты этих эпох. Для этого требуются дополнительные предположения. В частности, мы предположим, что контракционный параметр одинаков для электросла-бой модели и КХД.

Далее мы принимаем, что электрослабая модель, лагранжиан которой включает минимальные слагаемые, пропорциональные ϵ ⁴ , восстанавливается в стандартном виде при своей характерной температуре T 4 = 100 ГэВ, а полная реконструкция КХД с минимальными слагаемыми в лагранжиане порядка ϵ ⁸ происходит при температуре T 8 = 0 . 2 ГэВ.

Обозначим через А уровень обрезания для 6 ^k , к = 2 , 4 , 6 , 8 , т.е. при 6 ^к <  А все слагаемые в лагранжиане, пропорциональные ϵ ^k , считаем пренебрежимо малыми. Наконец, предположим, что контракционный параметр зависит от температуры

( T ) = ( 4)’.

q >  0 ,

где A — постоянная размерности T . Из уравнения для КХД 6 ⁸ ( T 8 ) = ( AT - 1 ) 8 q = А получаем A = T 8 А ¹ / ⁸ q = 0 , 2А ¹ / ^{8 q} ГэВ. Из подобного уравнения для электрослабой модели находим уровень обрезания А = ( T 8 T - 1 ) 8 ^q = (0 , 2 ■ 10 - ² ) ^{8 q} и (10 - ²² ) ^q , а также размерную константу A = T 2 T - ¹ = 4 ■ 10 - ⁴ ГэВ. Используя уравнение для к -ой степени 6 ^к ( T _k ) = ( AT - 1 ) ^qk = А , имеем

_T 1 - _k ⁸

T k = T 8 -8                   (76)

T 4

и легко находим граничные значения (ГэВ):

T 2 = 10 7 , T 4 = 10 2 , T 6 = 1 , T 8 = 2 ■ 10 ^{- 1} , (77)

не зависящие от степени q , связывающей параметр контракции и температуру (75). Оценка «бесконечной» температуры T 2 и 10 7 ГэВ намного меньше энергии Планка и 10 19 ГэВ, при которой становится существенным влияние гравитации. Таким образом, полученная эволюция элементарных частиц не выходит за пределы проблем, описываемых электрослабыми и сильными взаимодействиями.

6.    Зависимость сечения рождения бозонов Хиггса от температуры

Диаграмма Фейнмана, описывающая доминантный механизм рождения и регистрации бозонов Хиггса в экспериментах на Большом адронном коллайдере, после преобразования полей калибровочных бозонов (26), дополненных преобразованием полей лептонов и кварков (27), (56), принимает вид, изображенный на рис. 1, где L обозначает пару электронов или мюонов [13].

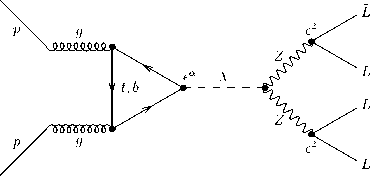
Рисунок 1. Модифицированная диаграмма рождения бозона Хиггса в четырехлептонном процессе.

Figure 1. Modified diagram of Higgs boson production in a four-lepton process.

Подсчет контракционных множителей в правой части диаграммы дает ϵ ⁴ . Этот множитель учитывает вклад элек-трослабых взаимодействий в рассматриваемый механизм. Оставшуюся часть диаграммы можно изобразить в виде петли виртуальных кварков (рис. 2), зависящей только от сильных взаимодействий.

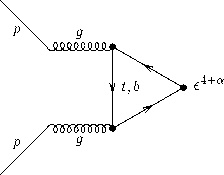
Рисунок 2. Диаграмма рождения бозона Хиггса, зависящая от сильных взаимодействий кварков. Здесь а = 1 для t -кварка и а = 2 для b -кварка.

Figure 2. Higgs boson production diagram dependent on strong quark interactions. Here а = 1 for the t -quark and а = 2 for the b -quark.

В результате контракции калибровочной группы КХД происходит «расщепление» процессов образования бозонов Хиггса при взаимодействии кварков на разные каналы, связанные с разной зависимостью цветов (компонент) кварков и глюонов от ϵ. Амплитуды Mik процессов рождения бозона Хиггса домножаются на контракционный параметр в различных степенях в зависимости от того, какие цветовые компоненты виртуальных кварков участвуют в его образовании. Сечение процесса пропорционально квадрату амплитуды aik = lMik |2. В силу малости параметра 6 = (AT - 1)q, q > 0 основной вклад в общее сечение при увеличении T дают каналы, пропорциональные параметру контракции с отрицательными степенями. Максимальный вклад вносит канал M31 (е) (рис. 3) с участием первой и третьей компонент t-кварка at (T) = T8 q atn, (78)

где ст¹" — непреобразованное сечение при е = 1 .

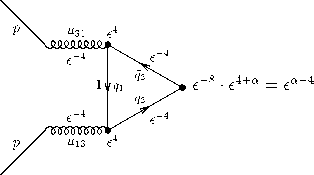
Рисунок 3. Петля виртуальных кварков с компонентами q 1 , q 3 и антикварка с компонентой q ₃ . Амплитуда канала M ₃₁ ( е ) .

Figure 3. A loop of virtual quarks with components q 1 , q 3 and an antiquark with component q ₃ . Channel amplitude M ₃₁ ( е ) .

Результаты измерений сечения рождения бозонов Хиггса в четырехлептонном распаде, полученные на БАК в течение ряда лет при столкновении протонных пучков разных энергий, приведены в обзоре [14]: a o = 17 при E = 7 , a tot = 22 при E = 8 , a tot = 56 при E = 13 , a o = 57 при E = 14 . Здесь E дано в ТэВ, а a o — в пикобарн. Из этих данных следует, что измеренные сечения демонстрируют квадратичную зависимость от энергии σ _tot ∼ E ² . Логично предположить, что температура T Вселенной и энергия E столкновения протонных пучков в БАК пропорциональны друг другу T ∼ E , тогда σ tot ^∼ T ^{2 .}

Сечение (78) для канала рождения t -кварка с амплитудой M 31 ( е ) имеет квадратичную зависимость a t ( T ) ~ T ² при q = 4 . Другие растущие сечения пропорциональны ~ T (тот же канал M ₃₁ ( е ) для b -кварка и канал M ₃₂ ( е ) для t -кварка). Вопрос о соотношении вкладов этих и других процессов в общее сечение σ _tot остается открытым. Экспериментальные сечения рождения бозонов Хиггса σ _tot содержат вклад как обоих t - и b -кварков, так и всех их цветов (компонент). Поэтому для прямого сравнения с теоретическими значениями необходимы дополнительные предположения о доле t - и b -петлевых вкладов в целом, о вкладах каждой цветовой компоненты кварков в общее сечение и др. Однако можно утверждать, что гипотеза о контракции калибровочной группы стандартной модели согласована с полученными экспериментальными данными по сечениям рождения бозонов Хиггса .

7.    Изменения частиц и взаимодействий в процессе эволюции

Разложение (73) лагранжиана стандартной модели по степеням контракционного параметра открывает возможность для построения промежуточных предельных моделей с разными частицами и взаимодействиями между ними. Можно взять лагранжиан L0 в качестве первоначальной предельной системы при T > 107 ГэВ, затем добавить L2 и получить вторую предельную модель с лагранжианом Lsm = L0 + L2 при 107 > T > 102 (ГэВ). После этого можно добавить L4 и получить следующую предельную модель L(4M = L0 + L2 + L4 при 102 > T > 1 (ГэВ) и так далее до полного восстановления лагранжиана стандартной модели при T < 2 ■ 10_ 1 ГэВ. По мере перехода от одной эпохи к другой изменяются значимые слагаемые в лагранжианах, что позволяет сделать некоторые выводы о частицах на разных стадиях эволюции Вселенной уже на уровне классических полей.

В пределе «бесконечной» температуры ( е = 0 , T >  10 7 ГэВ) получаем лагранжиан L 0 стандартной модели, квадратичные слагаемые которого содержат: безмассовые нейтрино и фотон, массивные Z -бозон и бозон Хиггса (29), (35), массивный монохроматический u -кварк (40) с первой ( R ) компонентой (59), (60). Слагаемые более высокого порядка описывают самодействие бозона Хиггса и его взаимодействие с Z -бозоном (31), слабые и электромагнитные взаимодействия нейтрино и u -кварка с фотоном и Z -бозоном (36), (41), а также взаимодействия диагональных глюонов (66). Отметим, что поля заряженных бозонов W _µ ^± , соответствующие подгруппе трансляций, не входят в предельный лагранжиан L 0 .

Из явного выражения лагранжиана взаимодействия следует, что частицы разного сорта не взаимодействуют между собой. Взаимодействуют только частицы одного вида, например, нейтрино взаимодействуют друг с другом посредством нейтральных токов. Все другие частицы являются заряженными и взаимодействуют посредством обмена Z бозонами и фотонами. Это выглядит как некая стратификация электрослабой модели с частицами одного вида в каждом слое.

При T >  10 7 ГэВ остаются отличными от нуля только две компоненты глюонного тензора напряженности F ,_v = д , A V - d v A , = 2 ( F RiR - F GG ) и F 8v = д , А V -d v A ⁸ = ^ 23 ( F R^R + F GG) , так что, используя (59), (60), (66), можно выписать предельный КХД лагранжиан в явной форме

(0) int (0)

^L = ^L U, 0 ^{+ L} u, 0 ^{+ L} gl =

= iu n Y ^ d ^ U R + g s | u r |² y ^ A ^RR -

1 f F^RR2 ² _ ¹ (p^GG2 ² - ¹ f^rrF^gg

4 \ ,v )     4 v ^p,v /     4 ^х ,v vv

Отсюда заключаем, что в этом пределе выживают только динамические слагаемые для одной цветовой компоненты u -кварка, т.е. кварки становятся монохроматическими. Также остаются ненулевыми слагаемые, описывающие взаимодействие этой компоненты с R -глюонами. Помимо R -глюонов присутствуют G -глюоны, которые не взаимодействуют с u _R . Таким образом, стратификация присутствует и в секторе КХД.

При температурах 107 ГэВ > T > 102 ГэВ к лагранжиану добавляется L2 , которое содержит кинетические слагаемые W±-бозонов (30), электронов (37) и d-кварков (42), а также описывает слабые взаимодействия W± с другими калибровочными бозонами (32) и бозоном Хиггса. Появляются взаимодействия нейтрино с электроном (38) и между u- и d-кварками (43). u-кварк обретают вторую цветовую степень свободы (61), которая взаимодействует с пер- вой (62). У d-кварка активируется первая цветовая степень свободы. Основная часть электрослабых и значительная часть цветовых взаимодействий восстанавливаются в эту эпоху.

При дальнейшем остывании до температур 10 2 ГэВ > T >  1 ГэВ к лагранжиану добавляется слагаемое L ₄ , которое обеспечивает слабые взаимодействия калибровочных бозонов между собой (33). Восстанавливаются все цветовые компоненты u -кварков (63) и взаимодействия между ними (64). У d -кварка появляется вторая цветовая степень свободы, сильно взаимодействующая с первой. Активизируется большое количество взаимодействий между глюонами (68).

В интервале температур 1 ГэВ ≥ T >  0 , 2 ГэВ появляется третья цветовая степень свободы d -кварка (63), присутствуют все цветовые взаимодействия за исключением (70). Наконец, при T ≤ 0 , 2 ГэВ в полном объеме восстанавливается стандартная модель.

Заключение

Рассмотрен предельный случай стандартной модели, соответствующий контракции ее калибровочной группы. Предполагается, что математический параметр контракции уменьшается при возрастании температуры Вселенной, а его нулевой предел соответствует «бесконечной» температуре, не превышающей планковскую энергию 10 ¹⁹ ГэВ. т.е. предел, где становятся существенными гравитационные взаимодействия. Другими словами, эволюция частиц не выходит за рамки проблем, описываемых элек-трослабыми и сильными взаимодействиями. Прослежены стадии развития стандартной модели в процессе эволюции Вселенной по мере ее остывания, которые различаются степенями контракционного параметра. Промежуточные лагранжианы L _k находятся с помощью уровня обрезания ∆ с учетом типичных энергий КХД и электрослабой модели. Их явный вид для каждой стадии развития стандартной модели получен из разложений (44),(71),(73) полных лагранжианов, что позволяет сделать выводы о развитии взаимодействий и свойств частиц в каждую из рассмотренных эпох.

Полученная схема эволюции частиц не противоречит разработанной из других соображений истории Вселенной [1, 8], согласно которой обусловленные КХД фазовые переходы происходят позже электрослабых фазовых переходов. Кроме того, она дает основу для более детального анализа этапов становления лептонов и кварк-глюонной плазмы, учитывая тот факт, что слагаемые L^ ) (69) и L^ ) (70) в глюонном лагранжиане L_gl (65) пренебрежимо малы при температурах от 0 . 2 до 100 ГэВ.

С другой стороны, в отличие от ТВО, наличие непрерывно изменяющегося параметра позволяет анализировать полученные результаты с точки зрения их зависимости от температуры. В частности, экспериментальные данные, полученные на Большом адронном коллайдере по сечениям рождения бозонов Хиггса при энергиях 7, 8, 13 и 14 ТэВ, не противоречат предложенной гипотезе.